Непрерывная
случайная величина может быть задана
не только с помощью функции распределения.
Введем понятие плотности
вероятности
непрерывной случайной величины.
Рассмотрим
вероятность попадания непрерывной
случайной величины на интервал [х,
х
+ Δх].
Вероятность такого события
P(х
≤ X
≤ х
+ Δх)
= F(х+
Δх)
– F(х),
т.е.
равна приращению функции распределения
F(х)
на этом участке. Тогда вероятность,
приходящаяся на единицу длины, т.е.
средняя плотность вероятности на участке
от х
до х+
Δх,
равна
.
Переходя к пределу
Δх
→ 0, получим плотность вероятности в
точке х:
,
представляющую
производную функции распределения
F(х).
Напомним, что для непрерывной случайной
величины F(х)
– дифференцируемая функция.
Определение.
Плотностью
вероятности
(плотностью
распределения)
f(x)
непрерывной
случайной величины Х называется
производная ее функции распределения
|
f(x) |
(4.8) |
Про случайную
величину Х
говорят, что она имеет распределение с
плотностью f(x)
на определенном участке оси абсцисс.
Плотность вероятности
f(x),
как и функция распределения F(x)
является одной из форм закона распределения.
Но в отличие от функции распределения
она существует только для непрерывных
случайных величин.
Плотность вероятности
иногда называют дифференциальной
функцией
или дифференциальным
законом распределения.
График плотности вероятности называется
кривой
распределения.
Пример 4.4.
По данным примера 4.3 найти плотность
вероятности случайной величины Х.
Решение.
Будем находить плотность вероятности
случайной величины как производную от
ее функции распределения f(x)
= F‘(x).

Отметим свойства
плотности вероятности непрерывной
случайной величины.
1.
Плотность
вероятности – неотрицательная функция,
т.е.
|
f(x) |
(4.9) |
как
производная монотонно неубывающей
функции F(x).
2.
Вероятность
попадания непрерывной случайной величины
Х в интервал [α,
β,]
равна
определенному интегралу от ее плотности
вероятности в пределах от α
до β,
т.е.
|
|
(4.10) |
Геометрически
вероятность попадания в интервал [α,
β,]
равна площади фигуры, ограниченной
сверху кривой распределения и опирающейся
на отрезок [α,
β,]
(рис.4.4).
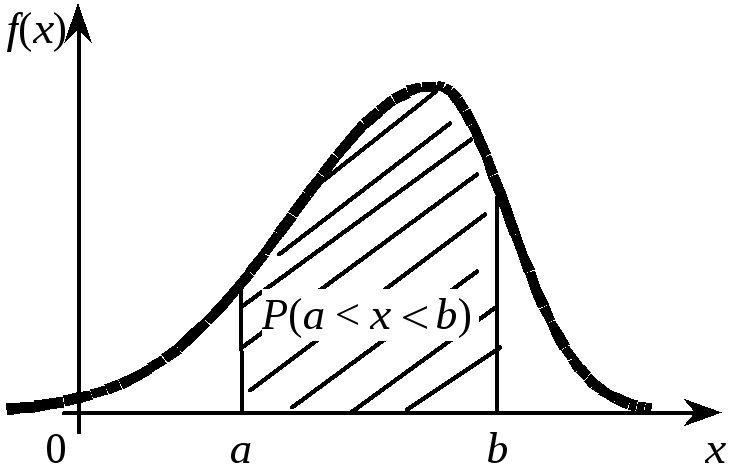
Рис. 4.4 Рис.
4.5
3.
Функция
распределения непрерывной случайной
величины может быть выражен через
плотность вероятности по формуле:
|
|
(4.11) |
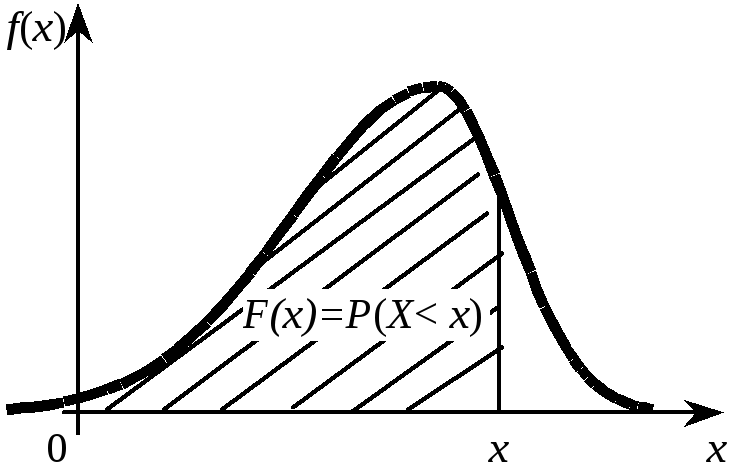
Геометрически
функция распределения равна площади
фигуры, ограниченной сверху кривой
распределения и лежащей левее точки х
(рис. 4.5).
4.
Несобственный
интеграл в бесконечных пределах от
плотности вероятности непрерывной
случайной величины равен единице:
|
|
(4.12) |
Геометрически
свойства 1
и 4
плотности вероятности означают, что ее
график – кривая распределения – лежит
не ниже оси абсцисс, а полная площадь
фигуры, ограниченной кривой распределения
и осью абсцисс, равна единице.
Пример 4.5.
Функция f(x)
задана в виде:
Найти: а) значение
А;
б) выражение функции распределения
F(х);
в) вероятность того, что случайная
величина Х
примет значение на отрезке [0; 1].
Решение.
а) Для того, чтобы f(x)
была плотностью вероятности некоторой
случайной величины Х,
она должна быть неотрицательна,
следовательно, неотрицательным должно
быть и значение А.
С учетом свойства 4
находим:
,
откуда А
=
.
б) Функцию
распределения находим, используя
свойство 3:
Если x
≤ 0, то f(x)
= 0 и, следовательно, F(x)
= 0.
Если 0 < x
≤ 2, то f(x)
= х/2
и, следовательно,
.
Если х
> 2, то f(x)
= 0 и, следовательно
.
в) Вероятность
того, что случайная величина Х
примет значение на отрезке [0; 1] находим,
используя свойство 2:
=
0,25. ◄
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Плотность распределения вероятностей непрерывной случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).
Плотностью распределения вероятностей непрерывной случайной величины
называют функцию
– первую производную от функции распределения
:
Из этого определения следует, что
функция распределения является первообразной для плотности распределения.
Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.
Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина
примет
значение, принадлежащее интервалу
равна
определенному интегралу от плотности распределения, взятому в пределах от
до
:
Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу
, равна площади криволинейной трапеции, ограниченной
осью
, кривой распределения
и прямыми
и
.
В частности, если
– четная
функция и концы интервала симметричны относительно начала координат, то:
Зная плотность распределения
можно найти
функцию распределения
по формуле:
Свойства плотности распределения
Свойство 1.
Плотность
распределения – неотрицательная функция:
Свойство 2.
Несобственный
интеграл от плотности распределения в пределах от
до
равен единице:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Интегральная функция распределения вероятностей
Примеры решения задач
Пример 1
Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики F(x) и f(x);
4) найти
математическое ожидание и дисперсию X;
5) найти
вероятность того, что X примет значение из
интервала (α,β):
α=1; β=1.7
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда
принадлежит
интервалу
.
Получаем:
3) Построим графики
и
:
График плотности распределения
График функции распределения
4)
Математическое ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
5)
Вероятность того, что случайная величина примет значение из интервала
:
Пример 2
Плотность
распределения вероятности непрерывной случайной величины равна
, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).
Решение
Нормировочный множитель
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
Пример 3
Непрерывная
случайная величина
имеет плотность распределения:
Найти
величину a, вероятность P(X<0) и математическое
ожидание X.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Постоянный
параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности имеет вид:
Вероятность:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Задачи контрольных и самостоятельных работ
Задача 1
Плотность
распределения непрерывной случайной величины X имеет вид:
Найти:
а)
параметр a;
б)
функцию распределения F(x);
в)
вероятность попадания случайной величины X в интервал (6.5; 11);
г)
математическое ожидание M(X) и дисперсию D(X);
Построить
график функций f(x) и F(x).
Задача 2
Задана
функция распределения непрерывной случайной величины:
Найти и
построить график функции плотности распределения вероятностей.
Задача 3
Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).
Задача 4
Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).
α=1,β=2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 5
Непрерывная
случайная величина
задана плотностью распределения вероятностей.
Требуется
найти:
— функцию
распределения вероятностей;
—
математическое ожидание;
—
дисперсию;
— среднее
квадратическое отклонение;
— вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;
—
построить графики функции распределения и плотности распределения вероятностей.
Задача 6
Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).
Задача 7
Случайная
величина X~N(a,σ)
a=25;
σ=4; α=13; β=30; δ=0.1.
Требуется:
—
составить функцию плотности распределения и построить ее график;
— найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);
— найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.
Задача 8
Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:
Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Случайная
величина X задана функцией распределения вероятностей F(x).
Требуется:
1. Найти
функцию плотности распределения f(x).
2. Найти M(X).
3. Найти
вероятность P(α<X<β)
4.
Построить графики f(x) и F(x).
α=2, β=4.5
Задача 10
Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).
M(X)=-1; D(X)=8
Задача 11
Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:
а) найти
параметр C;
б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);
в)
построить графики функций F(x) и f(x);
г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);
д)
вычислить вероятность попадания в интервал P(a≤x≤b)
е)
определить, квантилем какого порядка является точка xp;
ж)
вычислить квантиль порядка p
a=π/4; b=π/3; xp=π/2; p=0.75
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Geometric visualisation of the mode, median and mean of an arbitrary unimodal probability density function.[1]
In probability theory, a probability density function (PDF), or density of an absolutely continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a relative likelihood that the value of the random variable would be equal to that sample.[2][3] Probability density is the probability per unit length, in other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.
In a more precise sense, the PDF is used to specify the probability of the random variable falling within a particular range of values, as opposed to taking on any one value. This probability is given by the integral of this variable’s PDF over that range—that is, it is given by the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. The probability density function is nonnegative everywhere, and the area under the entire curve is equal to 1.
The terms probability distribution function and probability function have also sometimes been used to denote the probability density function. However, this use is not standard among probabilists and statisticians. In other sources, «probability distribution function» may be used when the probability distribution is defined as a function over general sets of values or it may refer to the cumulative distribution function, or it may be a probability mass function (PMF) rather than the density. «Density function» itself is also used for the probability mass function, leading to further confusion.[4] In general though, the PMF is used in the context of discrete random variables (random variables that take values on a countable set), while the PDF is used in the context of continuous random variables.
Example[edit]
Suppose bacteria of a certain species typically live 4 to 6 hours. The probability that a bacterium lives exactly 5 hours is equal to zero. A lot of bacteria live for approximately 5 hours, but there is no chance that any given bacterium dies at exactly 5.00… hours. However, the probability that the bacterium dies between 5 hours and 5.01 hours is quantifiable. Suppose the answer is 0.02 (i.e., 2%). Then, the probability that the bacterium dies between 5 hours and 5.001 hours should be about 0.002, since this time interval is one-tenth as long as the previous. The probability that the bacterium dies between 5 hours and 5.0001 hours should be about 0.0002, and so on.
In this example, the ratio (probability of dying during an interval) / (duration of the interval) is approximately constant, and equal to 2 per hour (or 2 hour−1). For example, there is 0.02 probability of dying in the 0.01-hour interval between 5 and 5.01 hours, and (0.02 probability / 0.01 hours) = 2 hour−1. This quantity 2 hour−1 is called the probability density for dying at around 5 hours. Therefore, the probability that the bacterium dies at 5 hours can be written as (2 hour−1) dt. This is the probability that the bacterium dies within an infinitesimal window of time around 5 hours, where dt is the duration of this window. For example, the probability that it lives longer than 5 hours, but shorter than (5 hours + 1 nanosecond), is (2 hour−1)×(1 nanosecond) ≈ 6×10−13 (using the unit conversion 3.6×1012 nanoseconds = 1 hour).
There is a probability density function f with f(5 hours) = 2 hour−1. The integral of f over any window of time (not only infinitesimal windows but also large windows) is the probability that the bacterium dies in that window.
Absolutely continuous univariate distributions[edit]
A probability density function is most commonly associated with absolutely continuous univariate distributions. A random variable 


Hence, if 

and (if 

Intuitively, one can think of 

![[x,x+dx]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f07271dbe3f8967834a2eaf143decd7e41c61d7a)
Formal definition[edit]
(This definition may be extended to any probability distribution using the measure-theoretic definition of probability.)
A random variable 






That is, f is any measurable function with the property that:
for any measurable set
Discussion[edit]
In the continuous univariate case above, the reference measure is the Lebesgue measure. The probability mass function of a discrete random variable is the density with respect to the counting measure over the sample space (usually the set of integers, or some subset thereof).
It is not possible to define a density with reference to an arbitrary measure (e.g. one can’t choose the counting measure as a reference for a continuous random variable). Furthermore, when it does exist, the density is almost unique, meaning that any two such densities coincide almost everywhere.
Further details[edit]
Unlike a probability, a probability density function can take on values greater than one; for example, the uniform distribution on the interval [0, 1/2] has probability density f(x) = 2 for 0 ≤ x ≤ 1/2 and f(x) = 0 elsewhere.
The standard normal distribution has probability density
If a random variable X is given and its distribution admits a probability density function f, then the expected value of X (if the expected value exists) can be calculated as
Not every probability distribution has a density function: the distributions of discrete random variables do not; nor does the Cantor distribution, even though it has no discrete component, i.e., does not assign positive probability to any individual point.
A distribution has a density function if and only if its cumulative distribution function F(x) is absolutely continuous. In this case: F is almost everywhere differentiable, and its derivative can be used as probability density:
If a probability distribution admits a density, then the probability of every one-point set {a} is zero; the same holds for finite and countable sets.
Two probability densities f and g represent the same probability distribution precisely if they differ only on a set of Lebesgue measure zero.
In the field of statistical physics, a non-formal reformulation of the relation above between the derivative of the cumulative distribution function and the probability density function is generally used as the definition of the probability density function. This alternate definition is the following:
If dt is an infinitely small number, the probability that X is included within the interval (t, t + dt) is equal to f(t) dt, or:
Link between discrete and continuous distributions[edit]
It is possible to represent certain discrete random variables as well as random variables involving both a continuous and a discrete part with a generalized probability density function using the Dirac delta function. (This is not possible with a probability density function in the sense defined above, it may be done with a distribution.) For example, consider a binary discrete random variable having the Rademacher distribution—that is, taking −1 or 1 for values, with probability 1⁄2 each. The density of probability associated with this variable is:
More generally, if a discrete variable can take n different values among real numbers, then the associated probability density function is:
where 

This substantially unifies the treatment of discrete and continuous probability distributions. The above expression allows for determining statistical characteristics of such a discrete variable (such as the mean, variance, and kurtosis), starting from the formulas given for a continuous distribution of the probability.
Families of densities[edit]
It is common for probability density functions (and probability mass functions) to be parametrized—that is, to be characterized by unspecified parameters. For example, the normal distribution is parametrized in terms of the mean and the variance, denoted by 

Different values of the parameters describe different distributions of different random variables on the same sample space (the same set of all possible values of the variable); this sample space is the domain of the family of random variables that this family of distributions describes. A given set of parameters describes a single distribution within the family sharing the functional form of the density. From the perspective of a given distribution, the parameters are constants, and terms in a density function that contain only parameters, but not variables, are part of the normalization factor of a distribution (the multiplicative factor that ensures that the area under the density—the probability of something in the domain occurring— equals 1). This normalization factor is outside the kernel of the distribution.
Since the parameters are constants, reparametrizing a density in terms of different parameters to give a characterization of a different random variable in the family, means simply substituting the new parameter values into the formula in place of the old ones.
Densities associated with multiple variables[edit]
For continuous random variables X1, …, Xn, it is also possible to define a probability density function associated to the set as a whole, often called joint probability density function. This density function is defined as a function of the n variables, such that, for any domain D in the n-dimensional space of the values of the variables X1, …, Xn, the probability that a realisation of the set variables falls inside the domain D is
If F(x1, …, xn) = Pr(X1 ≤ x1, …, Xn ≤ xn) is the cumulative distribution function of the vector (X1, …, Xn), then the joint probability density function can be computed as a partial derivative
Marginal densities[edit]
For i = 1, 2, …, n, let fXi(xi) be the probability density function associated with variable Xi alone. This is called the marginal density function, and can be deduced from the probability density associated with the random variables X1, …, Xn by integrating over all values of the other n − 1 variables:
Independence[edit]
Continuous random variables X1, …, Xn admitting a joint density are all independent from each other if and only if
Corollary[edit]
If the joint probability density function of a vector of n random variables can be factored into a product of n functions of one variable
(where each fi is not necessarily a density) then the n variables in the set are all independent from each other, and the marginal probability density function of each of them is given by
Example[edit]
This elementary example illustrates the above definition of multidimensional probability density functions in the simple case of a function of a set of two variables. Let us call 

Function of random variables and change of variables in the probability density function[edit]
If the probability density function of a random variable (or vector) X is given as fX(x), it is possible (but often not necessary; see below) to calculate the probability density function of some variable Y = g(X). This is also called a “change of variable” and is in practice used to generate a random variable of arbitrary shape fg(X) = fY using a known (for instance, uniform) random number generator.
It is tempting to think that in order to find the expected value E(g(X)), one must first find the probability density fg(X) of the new random variable Y = g(X). However, rather than computing
one may find instead
The values of the two integrals are the same in all cases in which both X and g(X) actually have probability density functions. It is not necessary that g be a one-to-one function. In some cases the latter integral is computed much more easily than the former. See Law of the unconscious statistician.
Scalar to scalar[edit]
Let 
Here g−1 denotes the inverse function.
This follows from the fact that the probability contained in a differential area must be invariant under change of variables. That is,
or
For functions that are not monotonic, the probability density function for y is
where n(y) is the number of solutions in x for the equation 

Vector to vector[edit]
Suppose x is an n-dimensional random variable with joint density f. If y = H(x), where H is a bijective, differentiable function, then y has density g:
with the differential regarded as the Jacobian of the inverse of H(⋅), evaluated at y.[5]
For example, in the 2-dimensional case x = (x1, x2), suppose the transform H is given as y1 = H1(x1, x2), y2 = H2(x1, x2) with inverses x1 = H1−1(y1, y2), x2 = H2−1(y1, y2). The joint distribution for y = (y1, y2) has density[6]
Vector to scalar[edit]
Let 







This result leads to the law of the unconscious statistician:
Proof:
Let 



It is clear that 

which is an upper triangular matrix with ones on the main diagonal, therefore its determinant is 1. Applying the change of variable theorem from the previous section we obtain that
which if marginalized over 
Sums of independent random variables[edit]
The probability density function of the sum of two independent random variables U and V, each of which has a probability density function, is the convolution of their separate density functions:
It is possible to generalize the previous relation to a sum of N independent random variables, with densities U1, …, UN:
This can be derived from a two-way change of variables involving Y = U + V and Z = V, similarly to the example below for the quotient of independent random variables.
Products and quotients of independent random variables[edit]
Given two independent random variables U and V, each of which has a probability density function, the density of the product Y = UV and quotient Y = U/V can be computed by a change of variables.
Example: Quotient distribution[edit]
To compute the quotient Y = U/V of two independent random variables U and V, define the following transformation:
Then, the joint density p(y,z) can be computed by a change of variables from U,V to Y,Z, and Y can be derived by marginalizing out Z from the joint density.
The inverse transformation is
The absolute value of the Jacobian matrix determinant 
Thus:
And the distribution of Y can be computed by marginalizing out Z:
This method crucially requires that the transformation from U,V to Y,Z be bijective. The above transformation meets this because Z can be mapped directly back to V, and for a given V the quotient U/V is monotonic. This is similarly the case for the sum U + V, difference U − V and product UV.
Exactly the same method can be used to compute the distribution of other functions of multiple independent random variables.
Example: Quotient of two standard normals[edit]
Given two standard normal variables U and V, the quotient can be computed as follows. First, the variables have the following density functions:
We transform as described above:
This leads to:
This is the density of a standard Cauchy distribution.
See also[edit]
- Density estimation
- Kernel density estimation
- Likelihood function
- List of probability distributions
- Probability amplitude
- Probability mass function
- Secondary measure
- Uses as position probability density:
- Atomic orbital
- Home range
References[edit]
- ^ «AP Statistics Review — Density Curves and the Normal Distributions». Archived from the original on 2 April 2015. Retrieved 16 March 2015.
- ^ Grinstead, Charles M.; Snell, J. Laurie (2009). «Conditional Probability — Discrete Conditional» (PDF). Grinstead & Snell’s Introduction to Probability. Orange Grove Texts. ISBN 978-1616100469. Archived (PDF) from the original on 2003-04-25. Retrieved 2019-07-25.
- ^ «probability — Is a uniformly random number over the real line a valid distribution?». Cross Validated. Retrieved 2021-10-06.
- ^ Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (for example, Table 5.1 and Example 5.4)
- ^ Devore, Jay L.; Berk, Kenneth N. (2007). Modern Mathematical Statistics with Applications. Cengage. p. 263. ISBN 978-0-534-40473-4.
- ^ David, Stirzaker (2007-01-01). Elementary Probability. Cambridge University Press. ISBN 978-0521534284. OCLC 851313783.
Further reading[edit]
- Billingsley, Patrick (1979). Probability and Measure. New York, Toronto, London: John Wiley and Sons. ISBN 0-471-00710-2.
- Casella, George; Berger, Roger L. (2002). Statistical Inference (Second ed.). Thomson Learning. pp. 34–37. ISBN 0-534-24312-6.
- Stirzaker, David (2003). Elementary Probability. ISBN 0-521-42028-8. Chapters 7 to 9 are about continuous variables.
External links[edit]
- Ushakov, N.G. (2001) [1994], «Density of a probability distribution», Encyclopedia of Mathematics, EMS Press
- Weisstein, Eric W. «Probability density function». MathWorld.
Про вероятности
Время на прочтение
11 мин
Количество просмотров 39K
(source)
Иногда мне приходится рассказывать другим людям как работает машинное обучение и, в частности, нейронные сети. Обычно я начинаю с градиентного спуска и линейной регрессии, постепенно переходя к многослойным перцептронам, автокодировщикам и свёрточным сетям. Все понимающе кивают головой, но в какой-то момент кто-нибудь прозорливый обязательно спрашивает:
А почему так важно, чтобы переменные в линейной регрессии были независимы?
или
А почему для изображений используются именно свёрточные сети, а не обычные полносвязные?
«О, это просто», — хочу ответить я. — «потому что если бы переменные были зависимыми, то нам пришлось бы моделировать условное распределение вероятностей между ними» или «потому что в небольшой локальной области гораздо проще выучить совместное распределение пикселей». Но вот проблема: мои слушатели ещё ничего не знают про распределения вероятностей и случайные переменные, поэтому приходится выкручиваться другими способами, объясняя сложнее, но с меньшим количеством понятий и терминов. А что делать, если попросят рассказать про батч нормализацию или генеративные модели, так вообще ума не приложу.
Так давайте не будем мучить себя и других и просто вспомним основные понятия теории вероятностей.
Случайные переменные
Представим, что у нас есть анкеты людей, где указаны их возраст, рост, пол и количество детей:
| age | height | gender | children |
|---|---|---|---|
| 32 | 175 | 1 | 2 |
| 28 | 180 | 1 | 1 |
| 17 | 164 | 0 | 0 |
| … | … | …. | …. |
Каждая строчка в такой таблице — это объект. Каждая ячейка — значение переменной, характеризующей этот объект. Например, возраст первого человека — 32 года, а рост второго — 180см. А что, если мы хотим описать некоторую переменную сразу для всех наших объектов, т.е. взять целую колонку? В этом случае у нас будет не одно конкретное значение, а сразу несколько, каждое со своей частотой встречаемости. Список возможных значений + соответсвующая вероятность и называется случайной переменной (random variable, r.v.).
Дискретные и непрерывные случайные переменные
Чтобы это отложилось в голове, я повторю ещё раз: случайная переменная полностью задаётся распределением вероятностей своих значений. Есть 2 основных типа случайных переменных: дискретные (discrete) и непрерывные (continuous).
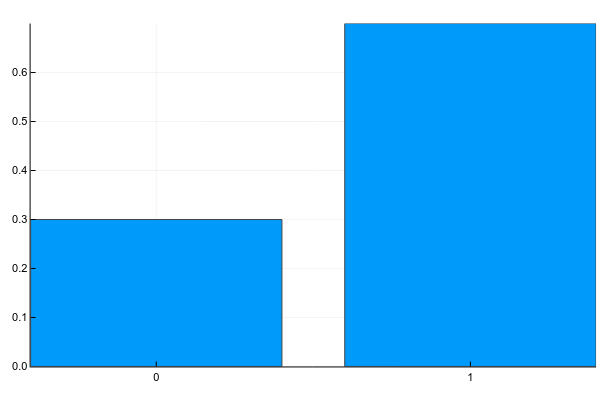
Дискретные переменные могут принимать набор чётко разделимых значений. Обычно я изображаю их как-нибудь так (probability mass function, pmf):
Код на Julia
Pkg.add("Plots")
using Plots
plotly()
plot(["0","1"], [0.3, 0.7], linetype=:bar, legend=false)А текстом это обычно записывается так (g — gender):
Т.е. вероятность того, что случайно взятый человек из нашей выборки окажется женщиной () равна 0.3, а мужчиной (
) — 0.7, что эквивалентно тому, что в выборке было 30% женщин и 70% мужчин.
К дискретным же переменным относятся количество детей у человека, частота встречаемости слов в тексте, количество просмотров фильма и т.д. Результат классификации на конечное число классов, кстати, — это тоже дискретная случайная переменная.
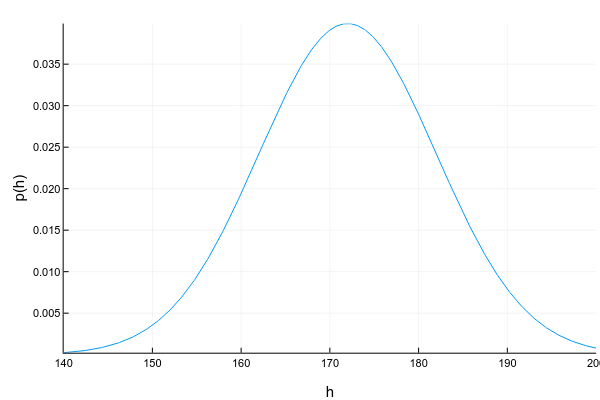
Непрерывные переменные могут принимать любое значение в определённом интервале. Например, даже если мы записываем, что рост человека — 175см, т.е. округляем до 1 сантиметра, на самом деле он может быть 175.8231см. Изображают непрерывные переменные обычно с помощью кривой плотности вероятности (probability density function, pdf):
Код
Pkg.add("Distributions")
using Distributions
xs = 140:0.1:200
ys = [pdf(Normal(172, 10), x) for x in xs]
plot(xs, ys; xlabel="h", ylabel="p(h)", legend=false, show=true)График плотности вероятности — штука хитрая: в отличие от графика массы вероятности для дискретных переменных, где высота каждой колонки показывает непосредственно вероятность получить такое значение, плотность вероятности показывает относительное количество вероятности вокруг некоторой точки. Саму же вероятность в этом случае можно посчитать только для интервала. Например, в этом примере вероятность, что случайно взятый человек из нашей выборки будет иметь рост от 160 до 170см равна примерно 0.3.
Код
d = Normal(172, 10)
prob = cdf(d, 170) - cdf(d, 160)Вопрос: может ли плотность вероятности в какой-то точке быть больше единицы? Ответ — да, конечно, главное, чтобы общая площадь под графиком (или, говоря математически, интеграл плотности вероятности) был равен единице.
Ещё одна трудность с непрерывными переменными состоит в том, что их плотность вероятности не всегда возможно красиво описать. Для дискретных переменных у нас просто была таблица значение -> вероятность. Для непрерывных это уже не прокатит, поскольку значений у них, вообще говоря, бесконечное множество. Поэтому обычно стараются аппроксимировать набор данных каким-нибудь хорошо изученным параметрическим распределением. Например, график выше — это пример т.н. нормального распределения. Плотность вероятности для него задаётся формулой:
где (мат. ожидание, mean) и
(дисперсия, variance) — параметры распределения. Т.е. имея всего 2 числа мы можем полностью описать распределение, посчитать его плотность вероятности в любой точке или суммарную веростность между двумя значениями. К сожалению, далеко не для любого набора данных найдётся распределение, которое сможет его красиво описать. Есть много способов бороться с этим (взять хотя бы смесь нормальных распределений), но это уже совсем другая тема.
Другие примеры непрерывного распределения: возраст человека, интенсивность пикселя на изображении, время ответа от сервера и т.д.
Совместное, маргинальное и условное распределения
Обычно мы рассматриваем свойства объекта не по одному, а в комбинации с другими, и здесь появляется понятие совместного распределения (joint probability) нескольких переменных. Для двух дискретных переменных мы можем изобразить его в виде таблицы (g — gender, c — # of children):
| c=0 | c=1 | c=2 | |
|---|---|---|---|
| g=0 | 0.1 | 0.1 | 0.1 |
| g=1 | 0.2 | 0.4 | 0.1 |
Согласно этому распределению, вероятность встретить в нашем наборе данных женщину с 2-мя детьми равна , а бездетного мужчину —
.
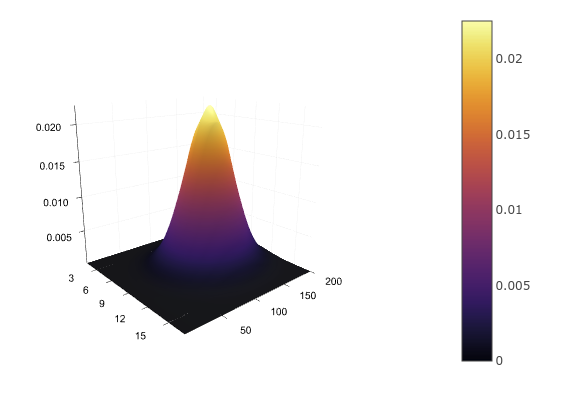
Для двух непрерывных переменных, например, роста и возраста, нам снова придётся задать аналитическую функцию распределения , аппроксимировав его,
например, многомерным нормальным. Таблицей это не запишешь, зато можно нарисовать:
Код
d = MvNormal([172.0, 30.0], [10 0; 0 5])
xs = 160:0.1:180
ys = 22:1:38
zs = [pdf(d, [x, y]) for x in xs, y in ys]
surface(zs)Имея совместное распределение, мы можем найти распределение каждой переменной по отдельности, просто суммировав (в случае дискретных) или интегрировав (в случае непрерывных) остальные переменные:
Это можно представить в виде суммирования по каждой строке или столбцу таблицы и вынесением результат на поля таблицы:
| c=0 | c=1 | c=2 | ||
|---|---|---|---|---|
| g=0 | 0.1 | 0.1 | 0.1 | 0.3 |
| g=1 | 0.2 | 0.4 | 0.1 | 0.7 |
Так мы снова получаем и
. Процесс вынесения на поля (margin) даёт название и самому получившемуся распределению — маргинальное (marginal probability).
А что, если мы уже знаем значение одной из переменных? Например, мы видим, что перед нами мужчина и хотим получить распределение вероятностей количества его детей? Таблица совместной вероятности и тут нам поможет: поскольку мы уже точно знаем, что перед нами мужчина, т.е. , мы можем выбросить из рассмотрения все остальные варианты и рассматривать только одну строчку:
| c=0 | c=1 | c=2 | |
|---|---|---|---|
| g=1 | 0.2 | 0.4 | 0.1 |
Поскольку вероятности так или иначе должны суммироваться в единицу, получившиеся значения нужно нормализовать, после чего получится:
Распределение одной переменной при известном значении другой называется условным (conditional probability).
Правило цепи
А соединяются все эти вероятности одной просто формулой, которая называется правилом цепи (chain rule, не путать с правилом цепи в дифференцировании):
Формула эта симметричная, поэтому так тоже можно:
Интерпретация правила очень простая: если — вероятность того, что я пойду на красный свет, а
— вероятность того, что человек, переходящий на красный свет, будет сбит, то совместная вероятность пойти на красный свет и быть сбитым как раз и равна произведению вероятностей этих двух событий. Но вообще лучше ходите на зелёный.
Зависимые и независимые переменные
Как уже говорилось, если у нас есть таблица совместного распределения, то мы знаем про систему всё: можно вычислить маргинальную веростность любой переменной, можно условное распределение одной переменной при известной другой и т.д. К сожалению, на практике составить такую таблицу (или просчитать параметры непрерывного распределения) в большинстве случаев невозможно. Например, если мы захотим посчитать совместное распределение встречаемости 1000 слов, то нам понадобится таблица из
107150860718626732094842504906000181056140481170553360744375038837035105112493612
249319837881569585812759467291755314682518714528569231404359845775746985748039345
677748242309854210746050623711418779541821530464749835819412673987675591655439460
77062914571196477686542167660429831652624386837205668069376
(чуть больше 1e301) ячеек. Для сравнения, количество атомов в наблюдаемой вселенной равно примерно 1e81. Пожалуй, покупкой дополнительной планки памяти тут не обойдёшься.
Но есть одна приятная деталь: не все переменные зависят друг от друга. Вероятность того, пойдёт ли завтра дождь, вряд ли зависит от того, перехожу ли я дорогу на красный свет. Для независимых переменных условное распределение одной от другой равно просто маргинальному распределению:
По-честному, совместная вероятность 1000 слов записывается так:
А вот если мы «наивно» предположим, что слова не зависят друг от друга, то формула превратится в:
А чтобы сохранить вероятности для 1000 слов нужна таблица всего с 1000 ячеек, что вполне приемлемо.
Почему тогда не считать все переменные независимыми? Увы, так мы потеряем массу информации. Представим, что мы хотим посчитать вероятность того, что пациент болен гриппом в зависимости от двух переменных: боли в горле и повышенной температуры. Отдельно боль в горле может говорить как о болезни, так и том, что пациент только что громко пел. Отдельно повышенная температура может говорить как о болезни, так и о том, что человек только что вернулся с пробежки. А вот если мы одновременно наблюдаем и температуру, и боль в горле, то это уже серьёзная причина выписать пациенту больничный.
Логарифм
Очень часто в литературе можно увидеть, что используется не просто вероятность, а её логарифм. Зачем? Всё довольно прозаично:
- Логарифм — монотонно возрастающая функция, т.е. для любых
и
если
, то и
.
- Логарифм произведения равен сумме логарифмов:
.
В примере со словами вероятность встретить любое слово , как правило, сильно меньше единицы. Если мы попробуем перемножить много маленьких вероятностей на компьютере с ограниченной точностью вычислений, догадываетесь что будет? Ага, очень быстро наши вероятности округляться к нулю. А вот если мы сложим много отдельных логарифмов, то выйти за пределы точности вычислений будет практически невозможно.
Условная вероятность как функция
Если после всех этих примеров у вас сложилось впечатление, что условная вероятность всегда вычисляется подсчётом количества раз, которое встретилось некоторое значение, то спешу развеять это заблуждение: в общем случае условная вероятность — это некоторая функция одной случайной переменной от другой:
где — это некоторый шум. Виды шума — это тоже отдельная тема, в которую мы сейчас влезать не будем, а вот на функции
остановимся поподробней. В примерах с дискретными переменными выше в качестве функции мы использовали простой подсчёт встречаемости. Это само по себе хорошо работает во многих случаях, например, в наивном байесовском классификаторе для текста или поведения пользователей. Чуть более сложная модель — линейная регрессия:
Здесь тоже делается предположение о том, что переменные независимы друг от друга, но распределение
уже моделируется с помощью линейной функции, параметры которой
нужно найти.
Многослойный перцептрон — это тоже функция, но благодаря промежуточным слоям, на которые влияют все входные переменные сразу, MLP позволяет моделировать зависимость выходной переменной от комбинации входных, а не только от каждой из них по отдельности (вспомните пример с болью в горле и температурой).
Свёрточная сеть работает с распределением пикселей в локальной области, покрываемой размером фильтра. Рекуррентные сети моделируют условное распределение следующего состояния от предыдущего и входных данных, а также выходной переменной от текущего состояния. Ну, в общем, вы поняли идею.
Теорема Байеса и умножение непрерывных переменных
Помните правило сети?
Если убрать левую часть, то получим простое и очевидное равенство:
А если теперь перенесём направо, то получим знаменитую формулу Байеса:
Про произношение
Итересный факт: русское произношение «байес» в английском звучит как слово «bias», т.е. «смещение». А вот фамилия учёного «Bayes» читается как «бэйс» или «бэйес» (лучше послушать в Yandex Translate).
Формула настолько избитая, что каждая её часть имеет своё название:
называется априорным распределением (prior). Это то, что мы знаем ещё до того, как увидели конкретный объект, например, общее количество людей, вовремя выплативших кредит.
носит название правдоподобия (likelihood). Это вероятность увидеть такой объект (описанный переменной
) при таком значении выходной переменной
. Например, вероятность того, что у человека, отдавшего кредит, двое детей.
— маргинальное правдоподобие, вероятность вообще увидеть такой объект. Оно одинаково для всех
, так что его чаще всего не считают, а просто максимизируют числитель формулы Байеса.
— апостериорное распределение (posterior). Это распределение вероятностей переменной
после того, как мы увидели объект. Например, вероятность того, что человек с двумя детьми отдаст кредит вовремя.
Байесовская статистика — штука жутко интересная, но влезать в неё сейчас мы не будем. Единственный вопрос, который хотелось бы затронуть, — это перемножение двух распределений непрерывных переменных, которое у нас встречается, например, в числителе формулы Байеса, да и вообще в каждой второй формуле над непрерывными переменными.
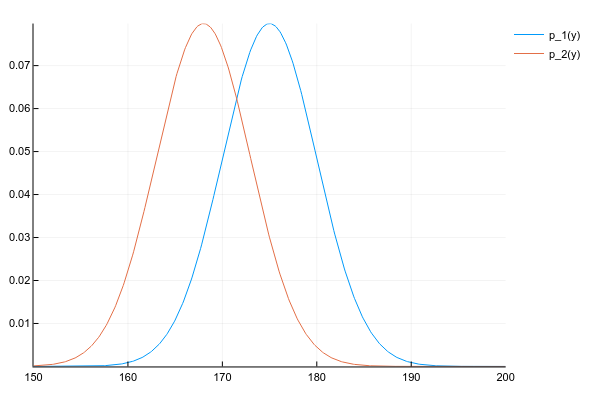
Допустим, что у нас есть два распределения и
:
Код
d1 = Normal(175, 5)
d2 = Normal(168, 5)
space = 150:0.1:200
y1 = [pdf(d1, y) for y in space]
y2 = [pdf(d2, y) for y in space]
plot(space, y1, label="p_1(y)")
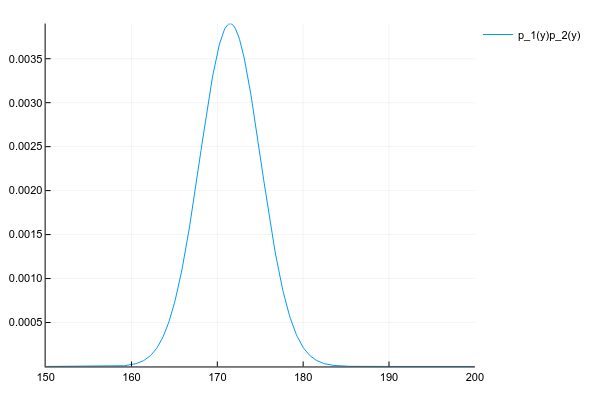
plot!(space, y2, label="p_2(y)")И мы хотим получить их произведение:
Мы знаем плотность вероятности обоих распределений в каждой точке, поэтому, по-честному и в общем случае, нам нужно перемножить плотности в каждой точке. Но, если мы вели себя хорошо, то и
у нас заданы параметрами, например, для нормального распределения 2-мя числами — матожиданием и дисперсией, а для их произведения придётся считать вероятность в каждой точке?
К счастью, произведение многих известных распределений даёт другое известное распределение с легко вычислимыми параметрами. Ключевое слово здесь — conjugate prior.
Как бы мы не вычисляли, произведение двух нормальных распределений даёт ещё одно нормальное распределение (правда, ненормализованное):
Код
# честно перемножаем плотности вероятности в каждой точке
# неэффективно, но работает для любых распределений
plot(space, y1 .* y2, label="p_1(y)p_2(y)")Ну и просто для сравнения распределение смеси 3х нормальных распределений:
Код
plot(space, [pdf(Normal(130, 5), x) for x in space] .+
[pdf(Normal(150, 20), x) for x in space] .+
[pdf(Normal(190, 3), x) for x in space])Вопросы
Раз уж это туториал и кто-нибудь наверняка захочет запомнить то, что здесь было написано, вот несколько вопросов для закрепления материала.
Пусть рост человека — нормально распределённая случайная переменная с параметрами
и
. Какова вероятность встретить человека ростом ровно 178см?
Ответ
Правильными ответами можно считать «0», «бесконечно мала» или «не определена». А всё потому что вероятность непрерывной переменной считается на некотором интервале. Для точки интервал — это её ширина, в зависимости от того, где вы учили математику, длину точки можно считать нулём, бесконечно малой или вообще не определённой.
Пусть
— количество детей у заёмщика кредита (3 возможными значения),
— признак того, отдал ли человек кредит (2 возможных значения). Мы используем формулу Байеса для предсказания, отдаст ли конкретный клиент с 1 ребёнком кредит. Сколько возможных значений может принимать априорное и апостериорное распределения, а также правдоподобие и маргинальное правдоподобие?
Ответ
Таблица совместного распредления двух переменных в данном случае небольшая и имеет вид:
| c=0 | c=1 | c=2 | |
|---|---|---|---|
| s=0 | p(s=0,c=0) | p(s=0,c=1) | p(s=0,c=2) |
| s=1 | p(s=1,c=0) | p(s=1,c=1) | p(s=1,c=2) |
где — признак успешно отданного кредита.
Формула Байеса в данном случае имеет вид:
Если все значения известны, то:
— это маргинальная вероятность увидеть человека с одним ребёнком, считается как сумма по колонке
и является просто числом.
— априорная/маргинальная вероятность того, что случайно взятый человек, про которого мы ничего не знаем, отдаст кредит. Может иметь 2 значения, соответствующих сумме по первой и по второй строке таблицы.
— правдоподобие, условное распределение количества детей в зависимости от успешности кредита. Может показаться, что раз уж это распределение количества детей, то возможных значений должно быть 3, но это не так: мы уже точно знаем, что к нам пришёл человек с одним ребёнком, поэтому рассматриваем только одну колонку таблицы. А вот успешность кредита пока под вопросом, поэтому возможны 2 варианта — 2 строки таблицы.
— апостериорное распределение, где мы знаем
, но рассматриваем 2 возможных варианта
.
Нейронные сети, оптимизирующие расстояние между двумя расспределениями
и
, зачастую используют в качестве оптимизационной цели кросс-энтропию (cross entropy) или расстояние Кульбака-Лейблера (Kullback-Leibler divergence). Последнее определяется как:
— это мат. ожидание по
, а почему в основной части —
— используется деление, а не просто разница между плотностями двух функций
?
Ответ
Другими словами, это и есть разница между плотностями, но в логарифмическом пространстве, которе является вычислительно более стабильным.



![{displaystyle Pr[aleq Xleq b]=int _{a}^{b}f_{X}(x),dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45fd7691b5fbd323f64834d8e5b8d4f54c73a6f8)



![{displaystyle Pr[Xin A]=int _{X^{-1}A},dP=int _{A}f,dmu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/591b4a96fefea18b28fe8eb36d3469ad6b33a9db)


![{displaystyle operatorname {E} [X]=int _{-infty }^{infty }x,f(x),dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00ce7a00fac378eafc98afb88de88d619e15e996)


















![{displaystyle g(mathbf {y} )=f{Bigl (}H^{-1}(mathbf {y} ){Bigr )}left|det left[left.{frac {dH^{-1}(mathbf {z} )}{dmathbf {z} }}right|_{mathbf {z} =mathbf {y} }right]right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/732bd3920089d7177a63016ab1717b6e0a56b654)


![{displaystyle operatorname {E} _{Y}[Y]=int _{mathbb {R} }yf_{Y}(y),dy=int _{mathbb {R} }yint _{mathbb {R} ^{n}}f_{X}(mathbf {x} )delta {big (}y-V(mathbf {x} ){big )},dmathbf {x} ,dy=int _{{mathbb {R} }^{n}}int _{mathbb {R} }yf_{X}(mathbf {x} )delta {big (}y-V(mathbf {x} ){big )},dy,dmathbf {x} =int _{mathbb {R} ^{n}}V(mathbf {x} )f_{X}(mathbf {x} ),dmathbf {x} =operatorname {E} _{X}[V(X)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad5325e96f2d76c533cb1a21d2095e8cf16e6fc7)














![{displaystyle {begin{aligned}p(y)&=int _{-infty }^{infty }p_{U}(yz),p_{V}(z),|z|,dz\[5pt]&=int _{-infty }^{infty }{frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}y^{2}z^{2}}{frac {1}{sqrt {2pi }}}e^{-{frac {1}{2}}z^{2}}|z|,dz\[5pt]&=int _{-infty }^{infty }{frac {1}{2pi }}e^{-{frac {1}{2}}left(y^{2}+1right)z^{2}}|z|,dz\[5pt]&=2int _{0}^{infty }{frac {1}{2pi }}e^{-{frac {1}{2}}left(y^{2}+1right)z^{2}}z,dz\[5pt]&=int _{0}^{infty }{frac {1}{pi }}e^{-left(y^{2}+1right)u},du&&u={tfrac {1}{2}}z^{2}\[5pt]&=left.-{frac {1}{pi left(y^{2}+1right)}}e^{-left(y^{2}+1right)u}right|_{u=0}^{infty }\[5pt]&={frac {1}{pi left(y^{2}+1right)}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63983efb2501c35f094487a9c6473a30e9405551)