1. Как определяют поток и плотность потока энергии электромагнитной волны?
Поток энергии электромагнитной волны — это энергия электромагнитного излучения, которое проходит сквозь поверхность площадью S в единицу времени.
Плотность потока энергии электромагнитной волны — это мощность электромагнитного излучения, которое проходит через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны.
2. Какая физическая величина характеризует перенос средней мощности электромагнитной волной?
Перенос средней мощности электромагнитной волной характеризуется интенсивностью электромагнитной волны.
3. Как интенсивность гармонической электромагнитной волны зависит от амплитуды напряженности электрического поля в волне?
Интенсивность гармонической электромагнитной волны прямо пропорциональна квадрату амплитуды напряженности электрического поля.
4. Как интенсивность электромагнитной волны зависит от расстояния до источника? Что можно сказать о зависимости напряженности электрического поля от этого расстояния?
Интенсивность электромагнитной волны обратно пропорциональна квадрату расстояния до источника. Напряженность электрического поля обратно пропорциональна расстоянию до источника.
5. Как интенсивность электромагнитной волны зависит от ее частоты? Объясните, почему энергетически выгодно излучение электромагнитных волн больших частот.
Интенсивность гармонической электромагнитной волны пропорциональна четвертой степени ее частоты. Так как излучение электромагнитных волн больших частот требует меньшей мощности передатчика, то оно энергетически более выгодно.
Вспомним, что волна — это колебания, распространяющиеся в пространстве. Механическая волна представляет собой колебания, распространяющиеся в вещественной среде. Тогда электромагнитная волна — это электромагнитные колебания, которые распространяются в электромагнитном поле.
Как появляются и распространяются электромагнитные волны
Представьте себе неподвижный точечный заряд. Пусть его окружают еще много таких зарядов. Тогда он будет действовать на них с некоторой кулоновской силой (и они на него). А теперь представьте, что заряд сместился. Это приведет к изменению расстояния по отношению к другим зарядам, а, следовательно, и к изменению сил, действующих на них. В результате они тоже сместятся, но с некоторым запаздыванием. При этом начнут смещаться и другие заряды, которые взаимодействовали с ними. Так распространяется электромагнитные взаимодействия.
Теперь представьте, что заряд не просто сместился, а он начал быстро колебаться вдоль одной прямой. Тогда по характеру движения он будет напоминать шарик, подвешенный к пружине. Разница будет только в том, что колебания заряженных частиц происходят с очень высокой частотой.
Вокруг колеблющегося заряда начнет периодически изменяться электрическое поле. Очевидно, что период изменений этого поля, будет равен периоду колебаний заряда. Периодически меняющееся электрическое поле будет порождать периодически меняющееся магнитное поле. Это магнитное поле, в свою очередь, будет создавать переменное электрическое поле, но уже на большем расстояние от заряда, и т.д. В результате появления взаимно порождаемых полей в пространстве, окружающем заряд, возникает система взаимно перпендикулярных, периодически меняющихся электрических и магнитных полей. Так образуется электромагнитная волна, которая распространяется от колеблющегося заряда во все стороны.
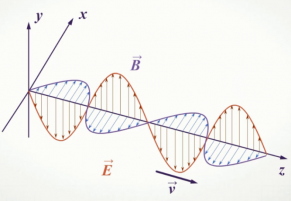
Электромагнитная волна не похожа на те возмущения вещественной среды, которые вызывают механические волны. Посмотрите на рисунок. На нем изображены векторы напряженности →E и магнитной индукции →B в различных точках пространства, лежащих на оси Oz, в фиксированный момент времени. Никаких гребней и впадин среды при этом не появляется.
В каждой точке пространства электрические и магнитные пол меняются во времени периодически. Чем дальше расположена точка от заряда, тем позднее ее достигнут колебания полей. Следовательно, на разных расстояниях от заряда колебания происходят с различными фазами. Колебания векторов →E и →B в любой точке совпадают по фазе.
Определение
Длина электромагнитной волны — расстояние между двумя ближайшими точками, в которых колебания происходят в одинаковых фазах.
Длина электромагнитной волны обозначается как λ. Единица измерения — м (метр).
Обратите внимание на рисунок выше. Векторы магнитной индукции и напряженности поля, являющиеся периодически изменяющимися величинами, в любой момент времени перпендикулярны направлению распространения волны. Следовательно, электромагнитная волна — поперечная волна.
Условия возникновения электромагнитных волн
Электромагнитные волны излучаются только колеблющимися заряженными частицами. При этом важно, чтобы скорость их движения постоянно менялась, т.е. чтобы они двигались с ускорением.
Наличие ускорения — главное условие возникновения электромагнитных волн.
Электромагнитное поле может излучаться не только колеблющимся зарядом, но и заряженной частицей, перемещающейся с постоянно меняющейся скоростью. Интенсивность электромагнитного излучения тем больше, чем больше ускорение, с которым движется заряд.
Представим заряд, движущийся с постоянной скоростью. Тогда создаваемые им электрическое и магнитное поля будут сопровождать его как шлейф. Только при ускорении заряда поля «отрываются» от частицы и начинают самостоятельное существование в форме электромагнитных волн.
Это интересно!
Впервые существование электромагнитных волн предположил Максвелл, который посчитал, что они должны распространяться со скоростью света. Но экспериментально они были обнаружены лишь спустя 10 лет после смерти ученого. Их открыл Герц. Он же подтвердил, что скорость распространения электромагнитных волн равна скорости света: c = 300 000 км/с.
Плотность потока электромагнитного излучения
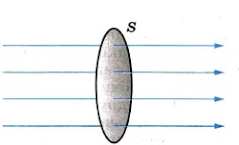
Излученные электромагнитные волны несут с собой энергию. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию.
На рисунке выше прямые линии указывают направления распространения электромагнитных волн. Это лучи — линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями.
Определение
Плотность потока электромагнитного излучения, или интенсивность волны — отношение электромагнитной энергии ΔW, проходящей за время Δt через перпендикулярную лучам поверхность площадью S, к произведению площади S на время Δt.
Плотность потока электромагнитного излучения обозначается как I. Единица измерения — Вт/м2 (ватт на квадратный метр). Поэтому плотность потока электромагнитного излучения фактически представляет собой мощность электромагнитного излучения, проходящего через единицу площади поверхности.
Численно плотность потока электромагнитного излучения определяется формулой:
I=ΔWSΔt
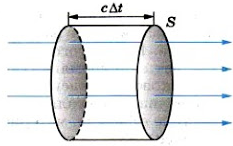
Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей cΔt (см. рисунок ниже).
Объем цилиндра: ΔV = ScΔt. Энергия электромагнитного поля внутри цилиндра равна произведению плотности энергии на объем: ΔW = wcΔtS. Вся эта энергия за время Δt пройдет через правое основание цилиндра. Поэтому получаем:
I=wcΔtSSΔt=wc
Следовательно, плотность потока электромагнитного излучения равна произведению плотности электромагнитной энергии на скорость ее распространения.
Определение
Плотность электромагнитной энергии — энергия электромагнитного излучения в единице объема. Обозначается как w. Единица измерения — Дж/м3.
Пример №1. Плотность потока излучения равна 6 мВт/м2. Найти плотность энергии электромагнитной волны.
I=wc
Отсюда:
w=Ic=6·10−33·108=2·10−11 (Джм3)
Точечный источник излучения
Источники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник.
Точечный источник — источник излучения, размеры которого много меньше расстояния, на котором оценивается его действие.
Предполагается, что точечный источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. В действительности таких источников не существует. Но за такие источники излучения можно принять звезды, так как расстояние между ними существенно больше размеров самих звезд.
Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.
Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4πR2. Если считать, что источник по всем направлениям за время Δt излучает суммарную энергию ΔW, получим:
I=ΔWSΔt=ΔW4πΔt·1R2
Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.
Пример №2. Плотность потока электромагнитного излучения на расстоянии 5 метров от точечного источника составляет 20 мВт/м2. Найти плотность потока электромагнитного излучения на расстоянии 10 метров от этого источника.
Расстояние по условию задачи увеличилось вдвое. Так как плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника, при увеличении расстояния вдвое интенсивность излучения уменьшится в 4 раза. То есть, она станет равной 5 мВт/м2.
Зависимость плотности потока излучения от частоты
Напряженность электрического поля и магнитная индукция электромагнитной волны пропорциональны ускорению заряда. Ускорение при гармонических колебаниях пропорционально квадрату частоты. Поэтому напряженность электрического поля и магнитная индукция также пропорциональны квадрату частоты:
E~a~ω2, B~a~ω2
Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. Поэтому плотность потока излучения I пропорциональна:
I~w
~(E2+B2)
Вспомним, что:
E~ω2, B~ω2
Тогда:
I~ω4
Плотность потока излучения пропорциональна четвертой степени частоты. Так, при увеличении частоты колебаний зарядов в 2 раза энергия, излучаемая ими, возрастает в 16 раз. При увеличении частоты в 3 раза, энергия излучения увеличивается в 81 раз, и т.д.
Пример №3. Частота электромагнитной волны уменьшилась в 4 раза. Найти, во сколько раз изменилась плотность потока излучения.
Так как плотность потока излучения пропорциональна четвертой степени частоты, мы можем найти плотность потока излучения путем извлечения корня из числа 4 дважды:
4√4=√√4=√2≈1,4
Плотность потока излучения уменьшилась в 1,4 раза.
Свойства электромагнитных волн
Современные радиотехнические устройства позволяют провести очень наглядные опыты по наблюдению свойств электромагнитных волн. При этом лучше всего пользоваться волнами сантиметрового диапазона. Эти волны излучаются специальным генератором сверхвысокой частоты (СВЧ). Электрические колебания генератора модулируют звуковой частотой. Принятый сигнал после детектирования подается на громкоговоритель.
| Свойство 1 — Поглощение электромагнитных волн | |
 |
Если расположить рупоры друг против друга и добиться хорошей слышимости звука в громкоговорители, а затем поместить между ними диэлектрик, звук будет менее громким. |
| Свойство 2 — Отражение электромагнитных волн | |
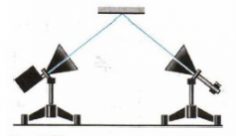 |
Если диэлектрик заменить металлической пластиной, то звук перестанет быть слышимым. Волны не достигают приемника вследствие отражения. Отражение происходит под углом, равным углу падения, как и в случае световых и механических волн. Чтобы убедиться в этом, рупоры располагают под одинаковыми углами к большому металлическому листу. Звук исчезнет, если убрать лист или повернуть его. |
| Свойство 3 — Преломление электромагнитных волн | |
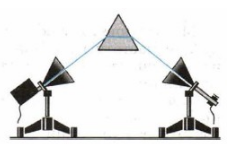 |
Электромагнитные волны изменяют свое направление (преломляются) на границе диэлектрика. Это можно обнаружить с помощью большой треугольной призмы из парафина. Рупоры располагают под углом друг к другу, как и при демонстрации отражения. Металлический лист заменяют затем призмой. Убирая призму или поворачивая ее, наблюдают исчезновение звука. |
| Свойство 4 — Поперечность электромагнитных волн | |
 |
Поместим между генератором и приемником решетку из параллельных металлических стержней. Решетку расположим так, чтобы стержни были горизонтальными или вертикальными. При одном из этих положений, когда электрический вектор параллелен стержням, в них возбуждаются токи, в результате чего решетка начинает отражать волны, подобно сплошной металлической пластине. Когда же вектор перпендикулярен стержням, токи в них не возбуждаются и электромагнитная волна проходит через решетку. |
Шкала электромагнитных волн
Электромагнитные волны имеют большое разнообразие. Они классифицируются по длине волны λ или связанной с ней частоте ν. Шкала электромагнитных волн включает в себя:
- радиоволны;
- оптическое излучение;
- ионизирующее излучение.
Укажем частоты и длины указанных волн, а также их подробную классификацию в таблице.
| Наименование диапазона волн | Длины волн (м) | Частоты (Гц) |
| Радиоволны | ||
| Инфразвук, звук | >105 | <3∙103 |
| Сверхдлинные волны (СДВ) | 104–105 | 3∙103–3∙104 |
| Длинные волны (ДВ) | 103–104 | 3∙104–3∙105 |
| Средние волны (СВ) | 102–103 | 3∙105–3∙106 |
| Короткие волны (КВ) | 10–100 | 3∙106–3∙107 |
Ультракороткие (УКВ):
|
|
|
| Оптические волны | ||
| Инфракрасное излучение | 0,78∙10–6–10–4 | 3∙1011–4∙1014 |
| Видимый свет | 0,38∙10–6–0,78∙10–6 | 4∙1014–7,5∙1014 |
| Ультрафиолетовое излучение | 10–7–0,38∙10–6 | 7,5∙1011–3∙1015 |
| Ионизирующее излучение | ||
| Рентгеновское излучение | 5∙10–12–10–8 | 3∙1016–6∙1019 |
| Гамма-излучение | <5∙10–12 | >6∙1019 |
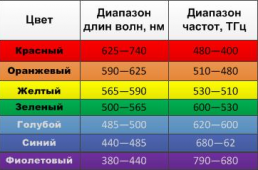
Частоты и длины волн электромагнитного излучения видимого спектра смотрите на рисунке ниже.
Задание EF17496
В электромагнитной волне, распространяющейся со скоростью →v, происходят колебания векторов напряжённости электрического поля →E и индукции магнитного поля →B. При этих колебаниях векторы →v, →E, →B. имеют взаимную ориентацию:
Ответ:
а) →B∥∥→E, →B∥∥→v, →E∥∥→v
б) →B⊥→E, →B∥∥→v, →E⊥→v
в) →B⊥→E, →B⊥→v, →E∥∥→v
г) →B⊥→E, →B⊥→v, →E⊥→v
Алгоритм решения
1.Вспомнить, какие величины периодически изменяются при распространении электромагнитной волны.
2.Вспомнить, какое взаимное расположение имеют векторы меняющихся величин электромагнитной волны.
3.Вспомнить, какой является электромагнитная волна — продольной или поперечной.
Решение
Электромагнитная волна представляет собой распространяющиеся с течением времени в пространстве электромагнитные колебания, характеризующиеся периодическим изменением в точках пространства вектора напряженности →E и вектора магнитной индукции →B. Эти векторы лежат и изменяются во взаимно перпендикулярных плоскостях. Поэтому вектора напряженности →E и вектор магнитной индукции →B перпендикулярны (→B⊥→E).
Электромагнитная волна — поперечная волна. Это значит, что векторы периодически меняющихся величин расположены перпендикулярно направлению распространения волны. Направление волны определяется направлением вектора ее скорости. Следовательно, вектор напряженности →E и вектор магнитной индукции →B перпендикулярны вектору скорости распространения волны (→B⊥→v, →E∥∥→v).
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17601
Какой объект, согласно классической электродинамике, не излучает электромагнитных волн?
Ответ:
а) ускоренно движущийся заряд
б) электромагнит, подключённый к генератору переменного тока
в) линия электропередачи
г) покоящийся электромагнит, подключённый к аккумулятору
Алгоритм решения
- Вспомнить основное условие возникновения электромагнитных волн.
- Проанализировать возможные источники электромагнитных волн и установить, в каком из них необходимое условие не выполняется.
Решение
Главное условие возникновения электромагнитных волн — наличие у движущегося заряда ускорения. Следовательно, ускоренно движущийся заряд излучает электромагнитные волны.
По линиям электропередачи протекает переменный ток, который периодически меняет свое направление. Следовательно, заряды внутри проводников движутся ускоренно, ведь для того, чтобы поменялась скорость (по модулю и направлению), необходимо наличие ускорения. Следовательно, линии электропередач тоже излучают электромагнитные волны. По этой же причине электромагнит, подключённый к генератору переменного тока, также излучает волны.
Покоящийся электромагнит, подключённый к аккумулятору, не может излучать электромагнитные волны. Аккумулятор — источник постоянного тока. Поэтому заряды движутся с постоянной скоростью (без ускорения), и сам электромагнит покоится (не имеет ускорения).
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17566
Выберите среди приведённых примеров электромагнитное излучение с минимальной длиной волны.
Ответ:
а) рентгеновское
б) ультрафиолетовое
в) видимое
г) инфракрасное
Алгоритм решения
- Вспомнить расположение видов волн на шкале.
- Определить тип волн, имеющих самую короткую длину волны из перечисленных вариантов.
Решение
Шкала электромагнитных волн классифицирует волны по длине или частоте волн. Чем меньше длина волны, тем выше ее частота. Наибольшей длиной волны обладают радиоволны, затем идем инфракрасное, видимое и ультрафиолетовое излучение. После — ионизирующее излучение (рентгеновское и гамма-излучение). Следовательно, наименьшей длиной волн из перечисленных вариантов обладает рентгеновское излучение.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.7k
Плотность потока энергии электромагнитной волны.
Запишем
,
.
В вакууме:
.
Умножим
и
на скорость электромагнитной волны,
получим
,
.
С учетом направления
векторов, запишем
,
.
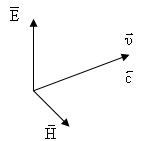
Величина в правой
части имеет смысл вектора плотности
потока энергии электромагнитной волны.
Обозначим этот вектор
.
,
,
.
Вектор
называется плотностью потока
электромагнитной волны или вектором
Пойнтинга.
Модуль плотности
потока электромагнитной волны равен
.
Направление вектора
совпадает с направлением скорости
электромагнитной волны.
Интенсивность волны.
Возьмем некоторую
произвольную поверхность
.
Поток энергии электромагнитной волны
через эту поверхность равен потоку
вектора
,
,
где
—
нормаль к элементу поверхности
.

Найдем среднее за
период значение потока энергии
,
.
Возьмем плоский
участок поверхности
,
перпендикулярный скорости волны
.
Запишем для него из
.

Запишем
,
Величина в правой
части имеет смысл энергии, переносимой
в 1с в среднем за период через единичную
площадку, перпендикулярную скорости
электромагнитной волны.
Она называется
интенсивностью электромагнитной волны.
,
,
.
Импульс электромагнитной волны.
Плоская
электромагнитная волна нормально падает
на плоскую поверхность проводника.
Выделим элемент проводника. Опыт дает,
что волна при этом проникает на некоторую
глубину
и исчезает, т.е. поглощается.
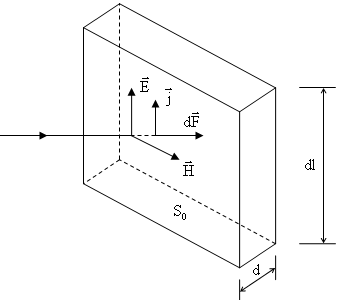
Электрическое
поле волны приводит к появлению
электрического тока, причем
,
.
На ток со стороны
магнитного поля волны действует сила
Ампера
,
,
где
—
объем элемента.
Электрический ток
совершает работу, которая идет на
увеличение внутренней энергии элемента
проводника
,
.
Разделим
,
.
Запишем для элемента
проводника 2-й закон Ньютона
,
,
,
где
—
импульс, который получает элемент
проводника за время
в результате действия силы
.
Проинтегрируем
по всей плоской поверхности проводника
,
.
Здесь
— модуль импульса, который получает
проводник за время
при падении на его поверхность
электромагнитной волны, энергия которой
.
Очевидно проводник может получить
импульс только от самой электромагнитной
волны.
Электромагнитная
волна, падающая на поверхность проводника,
поглощается в нем и при этом передает
проводнику свой импульс, которым
обладает, т.е. импульс электромагнитной
волны равен
.
Итак, электромагнитная
волна с энергией
обладает импульсом, модуль которого
равен
.
Энергию волны
находим интегрированием
.
Продифференцируем
по объему
.
Обозначим
,
где
— импульс электромагнитной волны в
единице объема пространства
.
Запишем
,
,
,
где
—
вектор Пойнтинга.
Давление электромагнитной волны.
Запишем для элемента
проводника
на который нормально падает электромагнитная
волна 2-й закон Ньютона
,
,
,
где
—
импульс электромагнитной волны, падающей
в течение
на участок проводника
.
Выделим объем в
виде параллелепипеда с гранями
и ребром
.
За время
волна дойдет от левой грани до грани
проводника
и поглотится. Следовательно,
,
где
—
объем параллелепипеда.
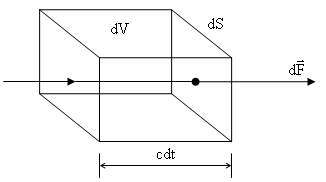
.
Сила
действует перпендикулярно к
,
т.е. является силой давления на
.
Разделим на
обе части
,
.
Обозначим:
—
давление,
,
.
Пусть волна падает
под углом
к нормали поверхности. В общем случае
,
.
—
коэффициент отражения,
—
полное поглощение,
—
полное отражение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Плотность энергии, которую переносят электромагнитные волны
Электромагнитные волны переносят энергию. Ее объемную плотность ($w$) составляют электрическое и магнитное поля, то есть:
где $w_E$ — плотность энергии электрического поля, $w_m$ — плотность энергии магнитного поля. При этом известно, что:
Для электромагнитной волны выполняется соотношение для мгновенных значений $E$ и $H$:
Из выражений (2) и (3), получается, что:
Иначе можно записать:
Из теории Максвелла следует вывод о том, что если тело полностью поглощает падающую на него перпендикулярно волну, то давление ($p$), которое она производит равно среднему значению объемной плотности энергии в данной волне:
Плотность импульса электромагнитной волны
При поглощении в веществе какого-нибудь тела электромагнитная волна оказывает на это тело давление, то есть сообщает ему импульс. Если обозначить плотность импульса как $overrightarrow{G}$, то его можно определить, используя вектор Умова — Пойнтинга ($overrightarrow{P}$):
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пусть плоская волна падает перпендикулярно на плоскую поверхность тела. Положим, что $varepsilon =1, mu =1$ плохо проводящего тела. Электрическое поле волны будет возбуждать в теле ток, плотность которого ($overrightarrow{j}$):
$sigma $ — удельная проводимость вещества. Магнитное поле волны действует на данный ток с удельной силой (${overrightarrow{F}}_u$) (силой на единицу объема):
Направление ${overrightarrow{F}}_u$ совпадает с направлением распространения волны.
При этом поверхностному слою тела толщиной $triangle l$, единичной площади волной сообщается импульс за $1 с$, ($overrightarrow{j}bot overrightarrow{H}$) равный:
В том же слое за $1 с$ поглощается энергия:
которая выделяется потом, как тепло. Найдем отношение импульса (10) к энергии (11), имеем:
Воспользуемся выражением (3) при $varepsilon =1, mu =1,$ получим:
Подставим (13) в формулу (13):
Из выражения (14) следует, что электромагнитная волна, обладающая энергией $W$, имеет импульс ($G$):
Из формулы (15) получаем, что плотность импульса ($G_u$) — импульс единицы объема равен:
«Плотность энергии и импульса электромагнитных волн» 👇
Воспользовавшись вектором Умова — Пойнтинга, можно выражение (16) представить как:
В формуле (17) учтено, что направление вектора импульса электромагнитной волны имеет такое же направление, что и вектор Умова — Пойнтинга.
Пример 1
Задание: Какое давление ($p$), производит плоская электромагнитная волна на тело? Она распространялась в вакууме, вдоль $оси X$, падает на тело перпендикулярно, поглощается полностью. Амплитуда напряженности магнитного поля равна $H_m$.
Решение:
В качестве основы для решения задачи примем вывод из теории Максвелла о том, что, если волна падает на тело перпендикулярно его поверхности и полностью поглощается, то:
[p=leftlangle wrightrangle left(1.1right),]
где $leftlangle wrightrangle $ — средняя объемная плотность энергии электромагнитной волны.
Уравнения колебаний модулей векторов напряженностей электрического и магнитного полей запишем в соответствии с гармоническими законами:
[E=E_m{cos left(omega t-kxright) }left(1.2right),] [H=H_m{cos left(omega t-kxright) }left(1.3right).]
Плотность энергии электромагнитного поля ($w$) является суммой плотности электрического поля ($w_E$) и плотности магнитного поля ($w_H$):
[w=w_E+w_Hleft(1.4right),]
где:
[w_E=frac{varepsilon varepsilon_0E^2}{2}, w_m=frac{mu mu_0H^2}{2}left(1.5right).]
При этом для электромагнитной волны мы имеем соотношение между мгновенными значениями характеристик полей:
[sqrt{varepsilon {varepsilon }_0}E=sqrt{mu {mu }_0}Hleft(1.6right).]
Следовательно, можем записать следующее:
[w=2w_m=2w_E=mu mu_0H^2left(1.7right).]
Используем выражение (1.3), подставив вместо H выражение, которое находится в правой части, получим:
[w=mu mu_0{H_m}^2{cos^2 left(omega t-kxright)left(1.8right). }]
Найдем среднее от объемной плотности энергии электромагнитной волны, получим:
[leftlangle wrightrangle =leftlangle mu {mu }_0{H_m}^2{cos^2 left(omega t-kxright) }rightrangle left(1.9right).]
Примем во внимание, что:
[leftlangle {cos^2 left(omega t-kxright) }rightrangle =frac{1}{2}left(1.10right).]
Тогда формула (1.9) будет переписана как:
[leftlangle wrightrangle =frac{mu {mu }_0{H_m}^2}{2}to p=frac{mu {mu }_0{H_m}^2}{2}.]
Ответ: $p=frac{mu {mu }_0{H_m}^2}{2}, где mu =1 .$
Пример 2
Задание: Чему равна средняя (по времени) плотность импульса электромагнитной волны ($leftlangle G_urightrangle $)? Если электромагнитная волна плоская, распространяется в вакууме по оси X, амплитуда ее магнитного поля равна $H_m.$
Решение:
За основу решения задачи примем формулу:
[overrightarrow{G_u}=frac{1}{c^2}left[overrightarrow{E}overrightarrow{H}right]to G_u=frac{1}{c^2}EHto leftlangle G_urightrangle =frac{1}{c^2}leftlangle EHrightrangle left(2.1right).]
Используя соотношение:
[sqrt{{varepsilon }_0}E_m=sqrt{{mu }_0}H_m(2.2)]
найдем амплитуду электрического поля:
[E_m=sqrt{frac{{mu }_0}{{varepsilon }_0}}H_mleft(2.3right).]
Уравнения колебаний модулей векторов напряженностей электрического и магнитного полей запишем в соответствии с гармоническими законами:
[E=E_m{cos left(omega t-kxright) }left(2.4right),] [H=H_m{cos left(omega t-kxright) }left(2.5right).]
Подставим выражения (2.3), (2.4) и (2.5) в формулу (2.1), получим:
[leftlangle G_urightrangle =frac{1}{c^2}leftlangle H_m{cos left(omega t-kxright)sqrt{frac{{mu }_0}{{varepsilon }_0}}H_m{cos left(omega t-kxright) } }rightrangle =frac{1}{c^2}sqrt{frac{{mu }_0}{{varepsilon }_0}}{H_m}^2leftlangle {cos^2 left(omega t-kxright) }rightrangle =frac{1}{{2c}^2}sqrt{frac{{mu }_0}{{varepsilon }_0}}{H_m}^2=frac{1}{{2c}^2}sqrt{frac{4pi cdot {10}^{-7}}{frac{1}{4pi cdot 9cdot {10}^9}}}{H_m}^2=frac{4pi cdot 3cdot 10}{{2c}^2}{H_m}^2=frac{60pi }{c^2}{H_m}^2.]
Ответ: $leftlangle G_urightrangle =frac{60 pi}{c^2}{H_m}^2.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме