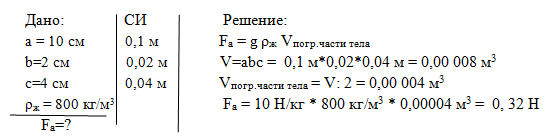Как найти плотность материала плавающего в воде

Условие задачи:

В воде плавает шар, погрузившись на 0,25 своего объема. Определить плотность материала шара.

Задача №3.3.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(V_{п}=0,25V), (rho-?)

Решение задачи:

Если шар плавает, значит сила Архимеда равна силе тяжести:

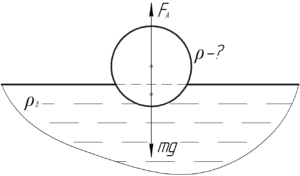
[{F_А} = mg]

Силу Архимеда находят по формуле:

[{F_А} = {rho _в}g{V_п}]

В этой формуле (rho_{в}) – плотность воды (жидкости, в которую погружен шар), (V_{п}) – объем погруженной части шара.

Массу шара можно найти как произведение плотности материала шара (rho) на его полный объем (V).

[m = rho V]

Тогда имеем:

[{rho _в}g{V_п} = rho Vg]

[{rho _в}{V_п} = rho V]

Так как по условию (V_{п}=0,25V), то:

[{rho _в} cdot 0,25V = rho V]

В итоге:

[rho  = 0,25{rho _в}]

Плотность воды равна 1000 кг/м³, поэтому плотность материала, из которого изготовлен шарик, равна:

[rho  = 0,25 cdot 1000 = 250;кг/м^3 = 0,25;г/см^3]

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.2.24 С какой силой давит атмосферный воздух на обложку книги размером 12×20 см2
3.3.2 Брусок дерева плавает в воде. Объем погруженной части бруска 36 см3. Определить
3.3.3 Льдина плавает на поверхности воды. Часть её объема, равная 150 м3, находится

В прошлых уроках мы познакомились с архимедовой силой и узнали о том, какие силы действуют в жидкости на погруженное в нее тело (архимедова сила и сила тяжести). Но разные тела ведут себя в жидкости по-разному: некоторые тонут, некоторые всплывают. Почему так происходит?

Какие условия провоцируют плавание? На этом уроке мы дополним свои знания о поведении тел, погруженных в жидкость.

Условия плавания тел

Рассмотрим ситуацию: мы полностью погружаем в жидкость тело и отпускаем его. Теперь на него действуют две противоположно направленные силы: сила тяжести и архимедова сила. Возможны три случая (рисунок 1).

При каком условии тело, находящееся в жидкости, тонет; плавает; всплывает?

Первый случай:
если сила тяжести $F_{тяж}$ больше архимедовой силы $F_A$, то тело будет двигаться ко дну — тонуть. 

Если $F_{тяж} > F_A$, то тело тонет.

Второй случай:
если сила тяжести $F_{тяж}$ равна архимедовой силе $F_A$, то тело будет находиться в равновесии в любом месте жидкости.

Если $F_{тяж} = F_A$, то тело плавает.

Третий случай:
если сила тяжести $F_{тяж}$ меньше архимедовой силы $F_A$, то тело будет двигать вверх в жидкости — всплывать.

Если $F_{тяж} < F_A$, то тело всплывает.

Вес жидкости, вытесненной плавающим телом

Как показать на опыте, что вес жидкости, вытесненной плавающим телом, равен весу тела в воздухе?
Рассмотрим подробнее третий случай и проведем опыт: в сосуд с трубкой для отлива (отливной сосуд) нальем воду до уровня трубки. Возьмем плавающее тело, взвесим его в воздухе и погрузим его в воду (рисунок 2).

После этого из трубки выльется вода, объем которой равен объему погруженной части тела. Мы можем взвесить эту воду. Тогда мы увидим, что ее вес равен весу тела в воздухе.

Вес этой воды будет эквивалентен архимедовой силе, а вес тела в воздухе — силе тяжести. Точно такой же эксперимент можно провести в разных жидкостях — результат мы получаем одинаковый.

Почему так происходит?
Когда мы погрузили плавающее тело в воду, оно стало всплывать ($F_{тяж} < F_A$). Что будет происходить с точки зрения физики в тот момент, когда тело достигнет поверхности воды?

При последующем подъеме архимедова сила будет уменьшаться, потому что будет постепенно уменьшаться объем той части тела, которая погружена в воду.

Когда же будет выполнено условие $F_{тяж} = F_A$, то тело перестанет всплывать и будет держаться (плавать) на поверхности воды, частично погрузившись в нее.

Если тело плавает в жидкости, то вес вытесненной им жидкости будет равен весу этого тела в воздухе.

Условие плавания тел и плотность жидкости

Рассмотрим простой опыт, изображенный на рисунке 3.

Сначала опустим железную гирю в сосуд с водой (рисунок 3, а). Гиря тонет. А теперь опустим железную гирю в сосуд со ртутью (рисунок 3, б) — гиря всплыла. Это произошло, потому что плотность железа больше плотности воды, но меньше плотности ртути.

Выводы: 

1. Когда плотность твердого тела больше плотности жидкости, в которую его погружают, то тело тонет.

Если $rho_т>rho_ж$, то тело тонет.

1. Когда плотность твердого тела меньше плотности этой жидкости, то оно всплывает:

Если $rho_т<rho_ж$, то тело всплывает.

1. Когда плотность твердого тела равна плотности жидкости, то тело остается в равновесии внутри жидкости:

Если $rho_т=rho_ж$, то тело плавает.

Теперь взглянем на следующий опыт, представленный на рисунке 4.

Здесь мы погрузили в воду два одинаковых шарика: пробковый и парафиновый. Видно, что часть пробкового шарика, погруженная в воду, меньше той же части парафинового.

Как зависит глубина погружения в жидкость плавающего тела от его плотности?
Известно, что плотность пробки меньше плотности парафина. Можно сказать, что чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость.

Несмешивающиеся жидкости также будут находиться в одном сосуде в соответствии со своими плотностями: в нижней части сосуда более плотные, в верхней — более легкие (рисунок 5). 

Плавание тел в природе

Почему водные животные не нуждаются в прочных скелетах?
В живой природе вес морских организмов почти полностью уравновешивается архимедовой силой, так как их плотность почти не отличается от плотности окружающей среды. Поэтому у морских животных легкие и гибкие скелеты, а у морских растений — эластичные стволы.

Каким образом рыбы могут менять глубину своего плавания и оставаться на ней? У каждой рыбы имеется плавательный (воздушный) пузырь (рисунок 6). 

Какую роль играет плавательный пузырь у рыб?
Пузырь легко сжимается и расширяется: при увеличении глубины за счет мышечных усилий увеличивается давление воды на рыбу. Плавательный пузырь сжимается, и объем тела рыбы уменьшается, уменьшается величина архимедовой силы, и рыба может спокойно оставаться на выбранной глубине. То же самое происходит при уменьшении глубины, но в обратную сторону: пузырь расширяется, объем всего тела рыбы увеличивается.

Как регулируют глубину погружения киты?
Киты и другие морские млекопитающие используют для изменения глубины собственные легкие подобно плавательному пузырю у рыб. 

Айсберг — это большой кусок льда, который свободно плавает в океане, так как плотность льда меньше плотности соленой воды (рисунок 7).

Обычно около $90 %$ объема айсберга находится под поверхностью воды, что делает столкновение с ним очень опасным. В 1912 году знаменитое судно «Титаник» столкнулось с айсбергом в Атлантическом океане. Оно затонуло, унеся с собой жизни 1513 пассажиров. Также айсберги являются огромными хранилищами пресной воды.

Упражнения

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

Ответ:

Тело в обоих случаях плавает. Мы знаем, что плотность жидкости будет больше там, где наше тело погружено в жидкость меньше (его меньшая часть находится под водой). Значит, плотность жидкости больше во втором случае (рисунок 9, б).

Можно рассмотреть этот вопрос с другой стороны. Плавающее тело вытесняет такой объем жидкости, который равен весу этого тела в воздухе. В первом случае (рисунок 9, а) тело вытеснило больше жидкости, чем во втором. Но вес этих объемов жидкости будет одинаковый. Значит, больший объем жидкости будет иметь меньшую плотность.

Наше тело плавает и в первом, и во втором случае. Поэтому сила тяжести и архимедова сила будут равны друг другу (рисунок 10).

Кроме того, архимедова сила, действующая на тело в первом сосуде, будет равна архимедовой силе, действующей на тело во втором сосуде. Сила тяжести тоже одинакова для обоих случаев.

Как архимедова сила может быть одинаковой, если жидкости имеют разную плотность?
Сила Архимеда зависит не только от плотности жидкости, но и от объема погруженного в нее тела ($F_А = g rho_ж V_т$). Так, во втором сосуде плотность жидкости больше, но объем погруженной части тела меньше.

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

Ответ:

На рисунке 12:

• а — тело плавает: $F_А = F_{тяж}$;
• б — тело всплывает: $F_А > F_{тяж}$;
• в — тело тонет: $F_А < F_{тяж}$.

Посмотреть ответ

Скрыть

Посмотреть ответ

Скрыть

Дано:
$V_1 = 100 space м^3$
$rho_л = 900 frac{кг}{м^3}$
$rho_в = 1030 frac{кг}{м^3}$

$m-?$
$V-?$

Посмотреть решение и ответ

Скрыть

Решение:

Отметим на рисунке силы, действующие на айсберг: $F_A$ и $F_т$.

Сила $F_A$ приложена к центру погруженной в воду части айсберга и направлена вверх.
Сила $F_т$ приложена к центру тела айсберга и направлена вниз.

Так как айсберг плавает (не тонет и не всплывает до конца), он находится в состоянии равновесия:
$F_A = F_т$
$F_A = rho_{в}gV_1$
$F_т = mg$
$rho_{в}gV_1 = mg$

Отсюда найдем массу айсберга:
$m = rho_{в}V_1$,
$m = 1030 frac{кг}{м^3} cdot 100 space м^3 = 103 space 000 space кг = 103 space т$.

Из определения объема:
$V = frac{m}{rho_л}$,
$V = frac {103 space 000 space кг}{900 frac{кг}{м^3}} approx 114 space м^3$

Ответ: $m = 103 space т$, $V approx 114 space м^3$.

Задание

Французский ученый Декарт (1596−1650) для демонстрации некоторых гидростатических явлений придумал прибор (рисунок 13). Высокий стеклянный сосуд (банку) наполняли водой, оставляя сверху сосуда небольшой объем воздуха. В этот сосуд опускали небольшую полую стеклянную фигурку. Фигурку заполняли частично водой и частично воздухом так, чтобы она только немного выходила из воды. Сверху стеклянный сосуд плотно закрывали куском тонкой кожи. Нажимая на кожу, можно было заставить фигурку плавать в воде и на воде, а также тонуть.

Изготовьте такой прибор («картезианский водолаз») и проделайте с ним опыты. Фигурку замените небольшим поплавком (пипеткой), а сосуд закройте резиновой пленкой (рисунок 14). Объясните действие прибора. Продемонстрируйте на этом приборе законы плавания тел.

Посмотреть ответ

Скрыть

Неоднократно тему «Плотность вещества»,
проходимую в 7 классе, обыгрывали и так и этак.
Однако, на моей практике еще никто не предлагал
эту тему как основу для прохождения темы
«Плавание тел». И не мудрено – ведь времени между
темами проходит почти 4 месяца.
Тем не менее, как показала практика, при
упоминании о плавании тел и, как следствие,
создание понятийной базы для этой темы можно и
нужно закладывать еще  раньше – а именно при
прохождении темы «Плотность вещества».
Это в лучшую сторону отражается и на понятийном
уровне самой темы «Плотность вещества» – ведь
при сравнении плотностей различных веществ
часто приходится ограничиваться парами «твердое
тело – твердое тело» и «жидкость – жидкость»
просто потому, что учащиеся еще не могут себе
представить жидкость тяжелее металла или камень
легче воды – они не трогали такое в руках, этого
не встретишь в обычной жизни… Зато каждый из них
видел, трогал и даже ел пастилу, молоко,
жевательный мармелад и кисель.
Подобная связь тем благотворно отражается на
каждой из них, ведь мы связываем их с жизненным
опытом учащихся, а определения и формулы прочно
завязываются на уже известные процессы.

Тип урока: урок изучения нового
материала.

Цель: ввести понятие плотности
вещества, научить уверенно сравнивать плотности
тел, находящихся в различных агрегатных
состояниях, показать практическую значимость
величины,  как для дальнейшего изучения
физики, так и для применения в жизни.

Задачи урока:

• Образовательные:
  • cформировать представление о плотности
    вещества как о величине, численно равной массе
    единицы объёма, умение определять плотность тел.
  • сформировать понятийную базу для дальнейшего
    изучения физики, а именно для темы «Плавание тел»
  • показать практическое применение усвоенных
    знаний в жизни и дальнейшем изучении физики
  • продолжить формирование ключевых компетенций
    учащихся: анализировать, обобщать, делать выводы
• Воспитательные:
  • продолжить формирование  системы взглядов на
    мир;
  • воспитывать интерес к творческой и
    исследовательский работе.
• Развивающие:
  • развивать речь, мышление;
  • совершенствовать умственную деятельность:
    анализ, синтез, классификация, способность
    наблюдать, делать выводы, выделять существенные
    признаки объектов, выдвигать гипотезы, проверять
    результаты;
  • развивать интерес к физике как  науки о
    природе.

Оборудование к уроку:

• Рабочая тетрадь
• Весы демонстрационные с разновесами
• Весы ученические с разновесами
• Несколько тел равных/разных объемов/масс
• Термос с сухим льдом (CO2)/ видеоролик с
  соответствующим опытом
• Жидкости разных плотностей
• Пастила и молоко или цилиндрики жевательного
  мармелада и кисель (не обязательно)
• Ноутбук, видеопроектор, экран
• Презентация к уроку «Плотность»
• Дополнительно: слайды 15-19 «Архимед и корона»

Домашнее задание: §21, определить
плотности 2-3 предметов домашнего обихода, 
рассчитать будут ли они плавать в морской воде,
масле, нефти.

План урока:

1. Организация начала урока – 3 мин.
2. Изучение нового материала – 20 мин.
3. Практическая работа  – 15 мин.
4. Рефлексия – 5 мин.
5. Подведение итогов урока – 2 мин.
6. Дополнительно просмотр слайдов 15-19 «Архимед и
   корона»

ХОД УРОКА

Организация начала занятия

Здравствуйте дети! Сегодня у нас будет не
совсем обычный урок и будет он проходить не в
обычном классе, а на кухне! Итак, представьте, что
мы на кухне…

Учитель надевает фартук и косынку.

1. Цель урока

Для того чтобы нам было удобней познавать
окружающий мир не только с точки зрения науки, но
и дома, в быту, мы должны уметь описывать свойства
и характеристики различных тел, и именно для
этого необходим сегодняшний урок, тема которого
называется «Плотность».
Слайд 1 – тема
А разобраться, что же это за понятие, нам поможет
поваренная книга… Выберем что-нибудь попроще.

2. Постановка проблемы

По рецепту, для того, чтобы приготовить
несколько бутербродов, необходимо взять около
300г сыра и столько же грамм хлеба.
Вот сыр, а что с хлебом? Давайте отрежем такой же
по форме и объему кусок хлеба. Вероятно, он будет
такой же по массе?

Дети отвечают – нет:

– Почему?
– Они разной массы! (Хлеб легче сыра. Всегда, или в
данной ситуации? Помним, что кусочки одинаковы по
объему).

Дети отвечают – да:

– Давайте проверим это!

Учитель приглашает к кафедре двух учеников, и
они сравнивают массу на весах.

– А теперь сравним несколько тел, которые
находятся у вас на столе.

Сравнивая массы и объемы тел 1, 2, 3 и 4 приходим
к выводу:

V₁ = V₂; тела изготовлены из
разных веществ: m₁ =/= m₂.
m₁ = m₂; тела изготовлены из
разных веществ: V₁ =/= V₂.

Слайд 1 – вывод

Вывод записываем в тетрадь

3. Изучение нового материала

Формулируем определение плотности вещества.

Для того, чтобы связать массу и объем тела, была
введена величина плотности, как отношения массы
тела к его объему.
Запишем определение в тетрадь.

Опр. Плотность – это физическая
величина, равная отношению массы тела к его
объему.

Слайд 1 – определение

Запись определения в тетради.

Обозначается плотность буквой ?,

Слайд 1 – обозначение
ее формула записывается прямо по определению:

Слайд 1 – формула

Запишем обозначения и единицы измерения всех
букв входящих в формулу плотности:
Иногда удобно брать несистемную единицу
измерения плотности – г/см³, выведем
соотношение между единицами измерения:

Слайд 2

Вывод записываем в тетрадь.

4. Систематизация знаний

У разных веществ разные плотности, и чем больше
плотность вещества, тем меньший объем оно будет
занимать.
Итак, чья плотность больше: сыра, или хлеба?

Дети отвечают.

Как мы уже выяснили сыр плотнее хлеба, и потому
у него будет меньший объем при такой же массе. Но
это твердые вещества, а как же жидкости? –
А теперь я приглашаю вас в бар.

Учитель показывает, как распределяются в
мензурке/фужере жидкости разных плотностей.

Какая из жидкостей имеет большую плотность?
Почему?
А если у нас будут газы разных плотностей?
Учитель показывает опыт с углекислым газом газом
или демонстрирует видео.
Для опыта потребуется сухой лед в металлическом
термосе и теплая вода.
Какой газ более плотный? Почему?
В нашей жизни нас окружает множество различных
веществ, плотности некоторых из них можно найти в
вашем учебнике, в таблицах на стр. 50-51.
Рассматриваем таблицы, особенно привлекаем
внимание ко льду, подсолнечному маслу, спирту,
молоку, чистой воде (то, что используется в
проверочном тесте)

Практическая работа

Отлично вы справились со всеми препятствиями
на пути к знаниям, а теперь, вернемся на кухню,
возьмем немного сладкого. Скажите, будет ли
пастила тонуть в молоке? Как это доказать?

Выполняем заполнение таблицы (слайд 3):

Сравниваем полученную плотность пастилы и
молока, делаем вывод и записываем его под
таблицей.

5. Подведение итогов урока. Рефлексия

Ну как, теперь вы знаете, что такое плотность?
А давайте проверим, насколько хорошо вы усвоили
это понятие.

Выполнение теста, слайды 4-6:

1.  Плотностью называют…

а)  физическую величину, равную отношению
объёма тела к его массе.
б)  физическую величину, равную отношению
массы тела к его объёму.
в)  физическое явление.

2.  В системе СИ  плотность измеряется в…

а)  г/см³.
б)  г/л.
в)  кг/м³.

3.  Стакан  с
подсолнечным маслом тяжелее…

а)  такого же стакана со спиртом.
б) такого же стакана с молоком.
в)  такого же стакана с чистой водой.

4. Бутерброд падает маслом вниз потому, что…

а) плотность масла больше плотности хлеба, и
даже малое количество масла тяжелее хлеба.
б) хлеб легче воздуха и потому всегда
поворачивается вверх.
в) масло скользкое.

5. Если кусочек льда опустить в спирт, то…

а) он будет плавать на поверхности.
б) он утонет.
в)  он взорвется.

Самопроверка теста, слайд 7:

Далее следует самооценка:

Поставьте по 1 баллу за каждый правильный
ответ на вопросы 1и 2, по 2 балла за каждый
правильный ответ на вопросы 3-4-5.

8 баллов – оценка «5»
6-7 баллов – оценка «4»
Менее 6 баллов –  вас ждет учебник физики и
хорошая оценка на следующем уроке.

6. Дополнительно:

Итак, мы познакомились с замечательной
величиной – плотностью. Где же она нам может
помочь?
Послушайте историю про Архимеда и корону:

Слайд 8

Об Архимеде и короне

Во время своего царствования в Сиракузах
Гиерон после благополучного окончания всех
своих мероприятий дал обет пожертвовать в
какой-то храм золотую корону бессмертным богам.
Он условился с мастером о большой цене за работу
и дал нужную ему массу золота. В назначенный день
мастер принес свою работу царю, который нашел ее
отлично исполненной; после взвешивания корона
оказалась соответствующей выданной массе
золота. После этого был сделан донос, что из
короны была взята часть золота и вместо него
примешано такое же количество серебра.
Гиерон разгневался на то, что его провели, и не
находя способа уличить это воровство, попросил
Архимеда хорошенько подумать об этом.
Тот, погруженный в думы по этому вопросу, как-то
случайно пришел в баню и там, опустившись в ванну,
заметил, что из нее вытекает такое же количество
воды, каков объем его тела, погруженного в ванну.
Выяснив себе ценность этого факта, он, недолго
думая, выскочил с радостью из ванны, пошел домой
голым и громким голосом сообщал всем, что он
нашел то, что искал. Он бежал и кричал одно и то же
по-гречески: «Эврика, эврика!» («Нашел,
нашел!)». Затем, исходя из своего открытия, он,
говорят, сделал два слитка, каждый такой же массы,
какого была корона, один из золота, другой из
серебра. Сделав это, он наполнил сосуд до самых
краев и опустил в него серебряный слиток, и,…
соответственное ему количество воды вытекло. Так
он нашел, какой масса серебра соответствует
какому то определенному объему воды. (То есть,
что он нашел? – плотность серебра). Затем он
произвел такое же исследование для золотого
слитка. Потом таким же методом был определен
объем короны. Она вытеснила воды больше, чем
золотой слиток и кража была доказана.

7. Решение задач (при наличии оставшегося
времени), запись домашнего задания:

Слайд 9

§ 1  Расчет архимедовой силы, условие плавания тел: формулы и определения

Рассмотрим решение задач на расчет архимедовой силы, условие плавания тел в жидкостях и газах.

Для решения задач нам нужно вспомнить следующие формулы и определения:

Архимедова силаравна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.

Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе: P выт.жидкости = P тела.

Морские и речные суда могут перевозить грузы. Вес груза зависит от водоизмещения судна. Водоизмещение — это вес воды, вытесненной судном, равный его весу в воздухе.

Подъемная сила аэростатовравна разности между архимедовой силы и весом оболочки, гондолы и газа, которым наполнен аэростат.

При решении задач важно верно выразить величины в системе СИ. 

Архимедова сила зависит от объема тела, поэтому вспомним размерности объема:

1 дм3 = 0,001 м3;

1 см3 = 0, 000 001 м3.

§ 2  Решение задач

Задача 1:Вычислите архимедову силу, действующую на брусок размером 2х10х4 см, если он наполовину погружен в спирт.

Решение:Запишем условие задачи. Нам известны размеры бруска: длина а = 10 см, ширина b=2 см, высота c=4 см. Плотность спирта ρж = 800 кг/м3. Выразим длину, ширину и высоту в системе СИ: 0,1 м, 0,02 м, 0,04 м.

Для решения запишем формулу вычисления архимедовой силы: Fa = gρжVпогр.части тела.

Объем всего бруска прямоугольной формы равен произведению длины на ширину и на высоту: V=abc = 0,1 м*0,02*0,04 м = 0,00 008 м3.

Объем погруженной части равен половине объема: Vпогр.части тела=0,00 004 м3.

Подставим числовые значения плотности спирта, коэффициента силы тяжести, объема погруженной части тела в формулу архимедовой силы и получим: Fa = 0,32 Н.

Ответ: на брусок в спирте действует архимедова сила 0,32 Н.

Задача 2:Какую силу нужно приложить к плите массой 4 т при ее подъеме со дна водоема, если объем плиты — 2 м3?

Решение:запишем условие задачи. Масса плиты m = 4 т, выразим в СИ: 4000 кг, объем плиты V = 2 м3, плотность воды ρж = 1000 кг/м3.

На тело, погруженное в жидкость или газ, действуют две силы: сила тяжести и архимедова сила, направленные противоположно. Поэтому вес плиты в воде уменьшается: Pв воде = Pв воздухе – Fа .

Вес тела в воздухе найдем по формуле P=mg, архимедову силу определим по формуле Fa = gρжVпогр. тела.

Тогда формула веса плиты в воде запишется так: Pв воде = mg — gρжVпогр. тела.

Подставим числовые значения величин, произведем вычисления и получим ответ: вес плиты в воде равен 20 000 Н, следовательно, для поднятия плиты в воде нужно приложить силу 20 кН.

Ответ: для поднятия плиты в воде нужно приложить силу 20 кН.

Задача 3: Какой по весу груз может удержать на поверхности воды пробковый пояс объемом 6,25 дм3 и массой 2 кг, если пояс будет погружен в воду полностью?

Решение: Запишем условие задачи. Нам известны объем пояса V = 6,25 дм3, его масса m = 2 кг, плотность воды ρж = 1000 кг/м3. Выразим объем в СИ, для этого 6, 25 поделим на 1000, равно 0,00 625 м3. Найти вес груза Pгр.

Известно, что вес груза, перевозимого судами, равен разности между водоизмещением судна и его весом. Водоизмещение — это вес воды, вытесненной судном с грузом. Тогда Pгруза = Pвытесненной воды — Pсудна.

Пробковый пояс при полном погружении вытесняет воду в объеме, равном объему пояса. Вычитая из веса вытесненной воды собственный вес пояса, можем найти вес груза:

Pгруза = Pвыт.воды – Pпояса.

Определим вес вытесненной воды. Для этого массу вытесненной воды умножим на коэффициент силы тяжести, а масса воды равна произведению плотности воды на ее объем. Объем вытесненной воды равен объему спасательного пояса. Тогда вес вытесненной воды равен произведению плотности воды на объем пояса и коэффициент тяжести:

Pвыт.воды = ρводы *Vводы *g

Определим вес пояса по формуле Pпояса =mпояса·g.

Подставим числовые значения величин и вычислим вес вытесненной поясом воды и вес пояса. Тогда вес груза равен их разности.

Ответ: пробковый пояс может удерживать в воде груз весом 42,5 Н.

Задача 4:Аэростат объемом 2000 м3 наполнен водородом. Вес оболочки и гондолы 16 000 Н. Определите подъемную силу аэростата.

Решение: Запишем условие задачи. Известны объем аэростата V = 2000 м3, вес оболочки и гондолы вместе Pоб =16 000 Н, плотность водорода, которым наполнен аэростат, ρгаза = 0,09 кг/м3, плотность воздуха при нормальном атмосферном давлении ρвозд. = 1,29 кг/м3. Все данные приведены в системе СИ. Требуется найти подъемную силу Fподъемн.

На аэростат действуют сила тяжести и архимедова сила, которая поднимает его вверх. Сила тяжести действует на оболочку, гондолу и газ, которым он наполнен. Вес оболочки и гондолы известен, нужно найти вес водорода, для этого массу водорода умножим на коэффициент тяжести. Массу водорода найдем по формуле плотности. Тогда вес газа равен произведению плотности газа на объем аэростата и коэффициент тяжести: Pгаза = ρгаза *Vаэростата *g.

Архимедову силу определим по формуле Fa = gρжVаэростата.

Подставим записанные формулы в формулу подъемной силы, вынесем одинаковые множители за скобки, вычислим.

Ответ: подъемная сила аэростата равна 8000 Н = 8 кН.

§ 3  Краткие итоги по теме урока

ВАЖНО ЗАПОМНИТЬ:

При решении задач нужно помнить основные формулы и определения.

Архимедова сила равна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.

Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе.

Водоизмещение — это вес воды, вытесненной судном с грузом, равный весу судна вместе с грузом. Вес груза, перевозимого судами или выдерживаемого спасательным поясом, плотом, льдиной, равен разности между весом вытесненной жидкости и весом самого судна, пояса, плота, льдины.

Подъемная сила аэростатов равна разности между архимедовой силы и весом аэростата (т.е. весом оболочки, гондолы и газа, которым наполнен аэростат).