Как найти плотность энергии магнитного поля соленоида

Проводник,
c
протекающим по нему электрическим ток,
всегда окружен магнитным полем, причем
магнитное поле исчезает и появляется
вместе с исчезновением и появлением
тока. Магнитное поле, подобно электрическому,
является носителем энергии. Логично
предположить, что энергия магнитного
поля совпадает с работой, затрачиваемой
током на создание этого поля.

Рассмотрим контур
индуктивностью L,
по которому протекает ток I.
С этим контуром сцеплен магнитный поток
Ф=LI,
поскольку индуктивность контура
неизменна, то при изменении тока на dI
магнитный поток изменяется на dФ=LdI.
Но для изменения магнитного потока на
величину dФ
следует совершить работу dА=IdФ=LIdI.
Тогда работа по созданию магнитного
потока Ф равна

Значит, энергия магнитного
поля, которое связано с контуром,

(1)

Энергию магнитного поля
можно рассматривать как функцию величин,
которые характеризуют это поле в
окружающем пространстве. Для этого
рассмотрим частный случай — однородное
магнитное поле внутри длинного соленоида.
Подставив в формулу (1) формулу индуктивности
соленоида, найдем

Так
как I=Bl/(μ0μN)
и В=μ0μH
, то

(2)

где
Sl
= V
— объем соленоида.

Магнитное поле внутри
соленоида однородно и сосредоточено
внутри него, поэтому энергия (2) заключена
в объеме соленоида и имеет с нем однородное
распределение с постоянной объемной
плотностью

(3)

Формула (3) для объемной
плотности энергии магнитного поля имеет
вид, аналогичный выражению для объемной
плотности энергии электростатического
поля, с тем отличием, что электрические
величины заменены в нем магнитными.
Формула (3) выводилась для однородного
поля, но она верна и для неоднородных
полей. Формула (3) справедлива только
для сред, для которых линейная зависимость
В от Н , т.е. оно относится только к пара-
и диамагнетикам.

Плотность
энергии магнитного поля в соленоиде с
сердечником будет складываться из
энергии поля в вакууме и в магнетике
сердечника:

,
отсюда

Т.к. в вакууме

, имеем

31.Напряженность магнитного поля. Диамагнетики и парамагнетики.

Напряженность
магнитного поля [H] – это отношение
магнитной индукции к магнитной
проницаемости среды

Напряженность
магнитного поля – величина векторная.
За единицу измерения напряженности
магнитного поля в Международной системе
единиц принят ампер на метр.

Если
в бесконечно длинном прямолинейном
проводе ничтожно малого кругового
сечения, помещенном в однородную среду,
протекает ток в 2π ампера, то в точках
магнитного поля, удаленных от оси провода
на расстояние 1 метра, напряженность
магнитного поля равна 1 а/м.

Рассмотрим,
как определяется направление магнитного
поля для случая прямолинейного проводника
и кольцевого тока.

Напряжение
магнитного поля прямолинейного проводника
с током определяет правило правого
винта: если винт ввинчивается так, чтобы
он поступательно перемещался по
направлению тока, то направление вращения
его головки будет совпадать с направлением
магнитных силовых линий.

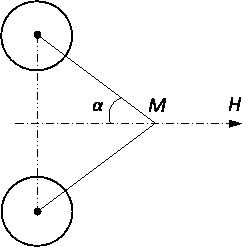
Напряженность
магнитного поля в какой-либо точке оси
МН кольцевого тока определяется по
формуле

где
I – ток в амперах;

R
– радиус кольца в метрах;

α
– угол, составленный осью кольца и
прямой линией, проведенной к средней
линии кольца из данной точки.

В
центре кольца на его оси, где α = 90,
напряженность магнитного поля определяется
по формуле

Направление
магнитного поля внутри кольца определяется
правилом буравчика: если вращательное
движение буравчика совпадает с
направлением тока в кольце, то
поступательное движение буравчика
совпадает с направлением магнитного
поля внутри кольца.

Напряженность
магнитного поля внутри соленоида большой
длины в точках на его оси определяется
по формуле

где
W – число витков соленоида;

l
– длина соленоида в метрах;

I
– ток в амперах.

Неаправление
магнитного поля внутри соленоида
определяется по правилу правой руки:если
правую руку положить на соленоид так,
чтобы четыре вытянутых пальца совпадали
с направлением тока в нем, то отставленный
большой палец покажет направление
выхода магнитных силовых линий. Магнитные
силовые линии выходят из северного
полюса и замыкаются на южном.

Вещества,
способные намагничиваться во внешнем
магнитном поле, т. е. создавать собственное
(внутреннее) магнитное поле самого
вещества называются магнетиками.
По своим магнитным свойствам магнетики
подразделяются на слабомагнитные
и сильномагнитные
вещества. К слабомагнитным
веществам относятся парамагнетики
и диамагнетики.
Основную группу сильномагнитных веществ
составляют ферромагнетики.
Слабо- и сильномагнитные вещества
отличаются величиной относительной
магнитной проницаемости μ.
Для слабомагнитных веществ μ
незначительно отличается от единицы:
для парамагнетиков μ≥1,
для диамагнетиков μ≤1.
Кроме того, μ
для слабомагнитных
веществ не зависит от индукции

того магнитного поля,
в котором намагничиваются вещества.
Для сильномагнитных веществ μ>>1
и зависит от

.

К парамагнетикам
относятся кислород, окись азота, алюминий,
платина, редкоземельные элементы,
щелочные и щелочноземельные металлы и
другие вещества. Парамагнетики
намагничиваются во внешнем магнитном
поле по направлению этого поля, т.е.
внутреннее поле парамагнетика

сонаправлено с внешним полем

(
↑↑
)
Для парамагнитных веществ μ
зависит от температуры
и убывает с повышением ее по закону:

(4.13)

где Т
— термодинамическая
температура, С — постоянная
Кюри, характерная для
данного вещества.

Диамагнетиками
являются инертные газы (гелий, аргон и
др.), многие металлы (золото, цинк, медь,
ртуть, серебро), вода, стекло, мрамор,
многие органические соединения.
Диамагнетики намагничиваются во внешнем
магнитном поле против направления этого
поля, т.е.

↑↓
.
Для этих веществ относительная магнитная
проницаемость не зависит от температуры.

Пара- и диамагнетики в
отсутствие внешнего магнитного поля
не способны намагничиваться, т.е. в них
не возникает внутреннее магнитное поле.

К ферромагнетикам
относится сравнительно небольшая группа
твердых кристаллических тел — так
называемых переходных металлов (железо,
никель, кобальт), а также ряд сплавов.
Ферромагнетики – это вещества, обладающие
спонтанной намагниченностью, т.е. они
обладают внутренним полем

при отсутствии внешнего магнитного
поля. Относительная магнитная проницаемость
μ
ферромагнетиков, в отличие от пара- и
диамагнетиков, имеет весьма большие
значения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Магнитное поле, связанное с электрическим током, характеризуется определенной энергией.

Если через проводник или катушку проходит ток, то часть электроэнергии расходуется на преодоление сопротивления проводника и превращается в тепло, а часть образует магнитное поле, в котором накапливается некоторая часть энергии, превращается в потенциальную энергию.

Определение магнитной энергии

Магнитная энергия и электростатическая потенциальная энергия связаны уравнениями Максвелла. Потенциальная энергия магнитного момента mm в магнитном поле BB определяется как механическая работа магнитной силы (фактически магнитного момента) на повторное выравнивание вектора магнитного дипольного момента и равна:

E=−m⋅BE = — m cdot B

в то время как энергия, запасенная в катушке индуктивности (с индуктивностью LL) при прохождении через нее тока II, определяется как:

E=1/2LI2E = 1/2 LI^2

Это выражение лежит в основе сверхпроводящего накопления магнитной энергии.

Энергия также хранится в магнитном поле. Энергия на единицу объема в области пространства проницаемости μ0μ0, содержащей магнитное поле BB, равна:

U=B2/2μ0U = B^2/2μ_0

В более широком смысле, если мы предположим, что среда является парамагнитной или диамагнитной и существует линейное определяющее уравнение, связывающее BB, то можно показать, что магнитное поле хранит энергию

E=12∫HBdV,E=frac{1}{2}int{HBdV},

где интеграл оценивается по всей области, где существует магнитное поле.

Аналогично энергию магнитного поля тока можно определить также через работу тока против ЭДС самоиндукции, которая выполняется при замыкании цепи.

Сравнивая выражение энергии магнитного поля через индукцию и силу тока с формулой для определения кинетической энергии, делаем вывод, что индуктивность в электромагнитных явлениях играет такую же роль, как масса в механических явлениях, и является мерой инертности электрической цепи.

Энергия магнитного поля соленоида

Определим энергию магнитного поля соленоида, индуктивность которого LL:

L=μμ0n02VL=mu {{mu }_{0}}n_{0}^{2}V

Wm=12μμ0n02I2V{{W}_{m}}=frac{1}{2}mu {{mu }_{0}}n_{0}^{2}{{I}^{2}}V.

Индукция магнитного поля внутри соленоида:

B=μμ0n0IB=mu {{mu }_{0}}{{n}_{0}}I

откуда

I=Bμμ0n0I=frac{B}{mu {{mu }_{0}}{{n}_{0}}}

Из данных формул получаем

Wm=12B2Vμμ0,{{W}_{m}}=frac{1}{2}frac{{{B}^{2}}V}{mu {{mu }_{0}}},

где VV –объем соленоида.

Поскольку поле соленоида однородно и почти полностью локализовано в его объеме, можно определить плотность энергии магнитного поля, то есть энергию, рассчитанную на единицу объема поля:

wm=WmV=12B2μμ0=BH2=μμ0H22{{w}_{m}}=frac{{{W}_{m}}}{V}=frac{1}{2}frac{{{B}^{2}}}{mu {{mu }_{0}}}=frac{BH}{2}=frac{mu {{mu }_{0}}{{H}^{2}}}{2}

Плотность энергии магнитного поля как характеристику поля относят к любой точке поля, в которых заданы векторы BB или HH.

Зная энергию магнитного поля, можно по теории относительности найти подходящую массу поля:

m=Wmc2m=frac{{{W}_{m}}}{{{c}^{2}}}

Итак, как электрическое, так и магнитное поля имеют не только энергию, но и массу. Эти поля так же материальны, как и вещества.

Тест по теме «Энергия магнитного поля»

Энергия магнитного поля и плотность энергии

Магнитное поле, создаваемое токами, распределено в пространстве. Рассмотрим, какова плотность энергии поля изолированного контура с током. Используем выражение для энергии магнитного поля, которое создано контуром с током:

$E_{m}=frac{LI^{2}}{2}left( 1 right)$.

где $I$ — сила тока в контуре; L – индуктивность контура.

Примем во внимание, что магнитный поток индукции через фиксированную неподвижную площадку пропорционален силе тока, а именно:

$Ф=LIleft( 2 right)$.

Из формулы (2) получим, что индуктивность контура равна:

$L=frac{Ф}{I}left( 3 right)$.

тогда энергия магнитного поля может быть представлена как:

$E_{m}=frac{ФI^{2}}{2I}=frac{ФI}{2}left( 4 right)$.

Магнитный поток из своего определения равен:

$Ф=intlimits_S {vec{B}bullet dvec{S}left( 5 right),}$

где $S$ – площадь поверхности контура с током. Вектор индукции магнитного поля запишем через векторный потенциал магнитного поля ($vec A$), который создается током $I$:

$vec{B}=rot, vec{A}left( 6 right)$

Тогда выражение (5) приведем к виду:

$Ф=intlimits_S {rot, vec{A}} dvec{S}=intlimits_L vec{A} bullet dvec{l}left( 7 right)$.

где $L$ — контур тока.

В выражении (7) векторный потенциал поля $vec{A}$ создан током, который течет в этом контуре, получается, что замкнутый ток взаимодействует с собственным магнитным полем.

Физическая сущность данного взаимодействия заключается в том, что всякий элемент тока $Ivec dl$ порождает в пространстве магнитное поле. С этим полем входят во взаимодействие все остальные элементы контура.

Подставим выражение для магнитного потока (7) в формулу для энергии (2), найдем:

$E_{m}=frac{I}{2}intlimits_L vec{A} bullet dvec{l}=frac{1}{2}intlimits_V vec{A} vec{j}dVleft( 8 right)$,

где сделан переход к объемным токам при помощи соотношения:

$vec{j}dVleftrightarrow Idvec{l}left( 9 right)$,

$vec j$ – вектор плотности тока.

Преобразуем выражение под интегралом так, чтобы в него входили только векторы поля и векторный потенциал. Используем формулы (6) и

$vec{j}=rot, vec{H, }left( 10 right).$

Вспомним известное соотношение для дивергенции векторного произведения:

$div(vec{A}times , vec{H})=vec{H}rot, vec{A}-vec{A}rotvec{H,}left( 11 right)$.

Получим в результате:

$vec{A}vec{j}=vec{H}vec{B}-div(vec{A}times vec{H})left( 12 right)$.

тогда выражение для энергии примет вид:

$E_{m}=frac{1}{2}int {vec{H}vec{B}dV} -int {div(vec{A}times vec{H})}dVleft( 13 right)$

Интеграл $int {div(vec{A}times vec{H})} dV$ в соответствии с теоремой Гаусса – Остроградского преобразуем в интеграл по поверхности, которая ограничивает объем интегрирования:

$intlimits_V {div(vec{A}times vec{H})dV} =intlimits_S {(vec{A}timesvec{H})dS, left( 14 right).} $

Будем считать, что все токи находятся в конечной области пространства. Тогда на больших расстояниях ($r$) от области локализации токов мы будем иметь:

1. $Asim frac{1}{r};$
2. $Hsim frac{1}{r^{2}}$.

В результате мы получаем, что подынтегральное выражение убывает пропорционально $sim frac{1}{r^{3}}$ . При этом поверхность интегрирования увеличивается пропорционально квадрату расстояния ($sim frac{1}{r^{2}}$). Вывод: с ростом расстояния от места расположения токов интеграл (14) убывает пропорционально расстоянию ($sim frac{1}{r}$). Следовательно, для всего пространства, когда $rto infty$ интеграл (4) стремится к нулю. Полную энергию магнитного поля представим в виде:

$E_{m}=frac{1}{2}int {vec{H}vec{B}dV} left( 15 right)$.

Из выражения (15) следует, что объемная плотность распределения энергии магнитного поля равна:

$w=frac{1}{2}vec{H}vec{B}left( 16 right)$.

Представленное выражение справедливо для равномерного распределения энергии поля по объему.

Формула (16) говорит нам о том, что объемная плотность энергии магнитного поля в каждой его точке определяют значения векторов поля в этой точке, и не имеет значение каковы источники поля.

Для однородного изотропного магнетика мы имеем следующую связь между векторами поля:

$vec{B}=mu mu_{0}vec{H}left( 17 right)$.

Используя формулу (17) выражения для нахождения плотности магнитного поля представим как:

$w=mu mu_{0}frac{H^{2}}{2}left( 18 right)$.

Или

$w=frac{B^{2}}{2mu_{0}}left( 19 right)$..

В Международной системе единиц (СИ) плотность энергии магнитного поля измеряется в джоулях, деленных на кубометр ($Дж/м^3$ ).

Энергия магнитного поля при наличии магнетиков

Допустим, что все пространство заполняет однородный магнетик. В этом случае создаваемая токами индукция будет изменяться в $frac{mu }{mu_{0}}$ раз в сравнении с индукцией в вакууме. ($mu$ – магнитная проницаемость вещества; $mu_{0}$ – магнитная постоянная). Это означает, что во столько же раз изменятся потоки $Ф$ и $dФ$. Из формулы (2) заключим, что индуктивность контура и взаимные индуктивности увеличатся в $frac{mu }{mu_{0}}$ раз. Формула (1) для энергии магнитного поля не изменится, но в ней индуктивность изменится в $frac{mu }{mu_{0}}$ раз.

Можно сделать вывод о том, что энергия магнитного поля токов, которые текут в неограниченном однородном магнетике, изменится в $frac{mu }{mu_{0}}$ раз в сравнении с энергией поля этих же самых токов в вакууме. Аналогичный вывод можно сделать относительно плотности энергии.

Ограниченность формул для вычисления плотности энергии

Допущения, сделанные нами, которые заставляют говорить об ограничениях применения формул, полученных нами для плотности энергии магнитного поля:

• Мы предполагали, что вещество, в котором токи создают магнитные поля, является магнитоизотропным. Магнитная проницаемость среды постоянная величина.
• Мы не учитывали, что поле осуществляет намагничивание вещества.

Вопрос о локализации энергии магнитного поля

Для постоянных магнитных полей, которые создаются неподвижными постоянными токами, непонятно, где локализуется энергия. Возьмем выражение для магнитной энергии соленоида:

$E_{m}=frac{IѰ}{2}left( 20 right)$),

где $Ѱ=BSN$ – потокосцепление, то есть магнитный поток через витки соленоида. В этом энергия поля кажется энергией тока, так как он является носителем.

Однако энергию соленоида можно представить и так:

$E_{m}=frac{B^{2}}{2mu mu_{0}}lS, left( 21 right)$.

где присутствуют параметры самого соленоида и характеристика магнитного поля ($B$), что говорит о том, что энергия поля распределена по объему поля.

Для постоянных магнитных полей эта непонятность вызвана тем, что токи и поля существуют неразрывно, образуя систему.

При переходе к переменным магнитным полям приемлемой становится только полевая концепция магнитной энергии, так как переменные магнитные поля входят как компоненты электромагнитных полей и могут существовать самостоятельно от токов. Электромагнитные волны переносят энергию, значит, сделаем вывод о том, что энергия магнитного поля распределена в объеме поля.

Продолжаем цикл статей о решении физических задач. Сегодня разберем несколько примеров на тему «Энергия магнитного поля».

Скучно решать задачи? Загляните на наш телеграм-канал, там много интересной и полезной информации для всех учащихся. А если хотите получить скидку на наши услуги, подписывайтесь на второй канал с приятными бонусами и акциями!

Энергия магнитного поля: задачи

Как решать физические задачи? Специально для новичков мы подготовили общую памятку, а также собрали вместе более 40 формул, которые обязательно пригодятся в учебе.

Кстати, в нашем блоге уже есть статья с задачами на  ЭДС самоиндукции и закон Фарадея. Всех интересующихся – милости просим.

Задача на энергию магнитного поля №1

Условие

Какова энергия магнитного поля соленоида, если по его обмотке индуктивностью L=0,2 Гн протекает ток I=10 А.

Решение

По определению, энергия магнитного поля равна:

W=LI22

Подставим значения, и вычислим:

W=0,2·1022=10 Дж

Ответ: 10 Дж.

Задача на энергию магнитного поля №2

Условие

Сила тока I в обмотке соленоида равна 1 А, а магнитный поток Ф через его поперечное сечение равен 0,1 мВб. Вычислить энергию магнитного поля соленоида, если он содержит N=1000 витков.

Решение

Для нахождения энергии магнитного поля будем использовать формуду из первой задачи. Очевидно, для вычисления нужно найти индуктивность. Выразим ее с помощью такой величины, как  потокосцепление – суммарный магнитный поток, сцепляющийся со всеми витками катушки:

ψ=LI=NФL=NФI

Подставим это выражение в формулу для энергии магнитного поля и высчислим ответ:

W=LI22=NФI2I·12=NФI2W=1000·0,1·10-3·12=0,05 Дж

Ответ: 0,05 Дж.

Задача на энергию магнитного поля №3

Условие

Плотность энергии w магнитного поля в железе равна 200 Дж/м3 при индукции поля B, равной 1 Тл. Какова магнитная проницаемость μ железа?

Решение

Запишем выражение для плотности энергии магнитного поля:

w= В22μ0μ

Выразим отсюда магнитную проницаемость и произведем вычисления:

μ=B22μ0w=122·1,26·10-6·200=2·103

Ответ: 2·103

Задача на энергию магнитного поля №4

Условие

Найти энергию магнитного поля соленоида, индуктивность которого 0,04 Гн, а магнитный поток через него составляет 0,5 Вб.

Решение

В данном случае для применения формулы W=LI22 не хватает величины I. Преобразуем данную формулу. Вспомним, что:

Ф=LII=ФL

Теперь первоначальную формулу для энергии магнитного поля можно записать в виде:

W=L2·Ф2L2=Ф22LW=0,522·0,04=3,125 Дж

Ответ: 3,125 Дж.

Задача на энергию магнитного поля №5

Условие

Какой должна быть сила тока в катушке с индуктивностью 0,8 Гн, чтобы энергия магнитного поля оказалась равной 2 Дж?

Решение

Запишем формулу для энергии магнитного поля и выразим из нее силу тока:

W=LI22I=2WL

Подставим значения из условия в формулу для силы тока и вычислим:

I=2·20,8=5=2,23 А

Ответ: 2,23 А.

Вопросы на тему «Энергия магнитного поля»

Вопрос 1. Что такое энергия магнитного поля?

Ответ. Магнитное поле обладает энергией. Эта физическая величина показывает, какую работу ток в проводнике (катушке индуктивности) затрачивает на создание данного магнитного поля. Энергия магнитного поля тока вычисляется по формуле:

W=LI22

Вопрос 2. Что такое объемная плотность энергии магнитного поля?

Ответ. Объемная плотность энергии магнитного поля определяет энергию поля в единице объема. Формула, выведенная Максвеллом для объемной плотности энергии магнитного поля соленоида:

w= B2μ0μ

Вопрос 3. От чего зависит энергия магнитного поля?

Ответ. Энергия магнитного поля прямо пропорциональна индуктивности.

Вопрос 4. Что такое индуктивность?

Ответ. Индуктивность – физическая величина, коэффициент пропорциональности между силой тока в контуре и магнитным потоком через контур, создаваемым данным током.

Индуктивность также называют коэффициентом самоиндукции, она характеризует магнитные свойства электрической цепи (контура, катушки и т.д.)

Вопрос 5. Как можно переписать формулу для энергии магнитного поля?

Ответ. Формула может быть записана в виде:

W=LI22=ФI2=Ф22L

Нужна помощь в решении задач или любых других заданий по учебе? Профессиональный сервис для студентов всегда готов поспособствовать с их решением.