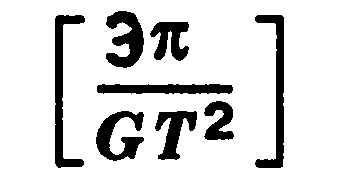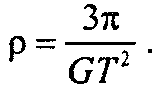Как найти плотность через период

Плотность планеты

Рассмотрим, как выразить ускорение свободного падения на поверхности планеты и первую космическую скорость для этой планеты через её радиус R и среднюю плотность 1 ρ.

1 Средняя плотность планеты равна отношению массы планеты к её объёму.

1. Выразите массу планеты М через её радиус R и среднюю плотность ρ.

2. Чему равно ускорение свободного падения g на поверхности планеты радиусом R, имеющей среднюю плотность ρ?

П о д с к а з к а. Воспользуйтесь формулой (8) из § 14, заменив массу и радиус Земли на массу и радиус данной планеты.

3. Вблизи поверхности планеты-гиганта Юпитер (на рисунке 18.1 Юпитер изображён в одном масштабе с Землёй) ускорение свободного падения в 2,6 раза больше, чем вблизи поверхности Земли. Радиус Юпитера примерно в 11 раз больше радиуса Земли. Какова средняя плотность Юпитера?

4. На планете радиусом 3400 км камень падает с обрыва высотой 200 м в течение 10 с. Чему равна средняя плотность планеты? Считайте, что сопротивлением атмосферы планеты можно пренебречь.

5. Чему равна первая космическая скорость для планеты радиусом R со средней плотностью ρ?

П о д с к а з к а. Воспользуйтесь формулой (10) из § 14, заменив радиус Земли и ускорение свободного падения на поверхности Земли на массу данной планеты и ускорение свободного падения на её поверхности.

А сейчас мы получим несколько неожиданный результат.

6. Чему равен период Т обращения спутника по низкой круговой орбите 2 вокруг планеты радиусом R со средней плотностью ρ?

2 В таком случае радиус орбиты можно считать равным радиусу планеты.

Итак, период обращения спутника на низкой круговой орбите зависит только от средней плотности планеты!

7. Астронавты облетели три планеты А, Б и В на низких круговых орбитах с выключенным двигателем. Время облёта каждой из планет составило: Т_A = 55 мин, Т_B = 106 мин, Т_B = 72 мин. У какой из этих планет наибольшая средняя плотность? У каких из этих планет средняя плотность больше средней плотности Земли? Напомним, что период обращения искусственного спутника Земли на низкой орбите 85 мин.

Источник

Плотность планеты. Суточное вращение планеты

1. Плотность планеты

Рассмотрим, как выразить ускорение свободного падения на поверхности планеты и первую космическую скорость для этой планеты через ее радиус R и среднюю плотность ρ. (Средняя плотность планеты равна отношению массы планеты к ее объему.)

? 1. Выразите массу планеты M через ее радиус R и среднюю плотность ρ.

? 2. Чему равно ускорение свободного падения g на поверхности планеты радиусом R, имеющей среднюю плотность ρ?

Подсказка. Воспользуйтесь формулой (8) из в § 14, заменив массу и радиус Земли на массу и радиус данной планеты.

? 3. Вблизи поверхности планеты-гиганта Юпитер (на рисунке 18.1 Юпитер изображен в одном масштабе с Землей) ускорение свободного падения в 2,6 раза больше, чем вблизи поверхности Земли. Радиус Юпитера примерно в 11 раз больше радиуса Земли. Какова средняя плотность Юпитера?

? 4. На планете радиусом 3400 км камень падает с обрыва высотой 200 м в течение 10 с. Чему равна средняя плотность планеты? Считайте, что сопротивлением атмосферы планеты можно пренебречь.

? 5. Чему равна первая космическая скорость для планеты радиусом R со средней плотностью ρ?

Подсказка. Воспользуйтесь формулой (10) из § 14, заменив радиус Земли и ускорение свободного падения на поверхности Земли на массу данной планеты и ускорение свободного падения на ее поверхности.

А сейчас мы получим несколько неожиданный результат.

? 6. Чему равен период T обращения спутника по низкой круговой орбите вокруг планеты радиусом R со средней плотностью ρ? (В таком случае радиус орбиты можно считать равным радиусу планеты.)

Итак, период обращения спутника на низкой круговой орбите зависит только от средней плотности планеты!

? 7. Астронавты облетели три планеты А, Б и В на низких круговых орбитах с выключенным двигателем. Время облета каждой из планет составило: T_А = 55 мин, T_Б = 106 мин, T_В = 72 мин. У какой из этих планет наибольшая средняя плотность? У каких из этих планет средняя плотность больше средней плотности Земли? Напомним, что период обращения искусственного спутника Земли на низкой орбите 85 мин.

2. Учет вращения планеты вокруг своей оси

Геостационарная орбита

Телевизионные программы передают в разные точки Земли с помощью спутников связи (рис. 18.2), которые движутся по круговым орбитам.

Сигнал со спутника принимает укрепленная на стене или крыше дома спутниковая антенна. Она направлена постоянно на одну и ту же точку небосвода, поэтому спутник связи должен постоянно «висеть» над одной и той же точкой поверхности Земли.

? 8. Чему равен период одного оборота спутника связи?

Орбиту, по которой движется спутник, находящийся постоянно над одной и той же точкой поверхности Земли, называют геостационарной. Она лежит в экваториальной плоскости Земли (так называют плоскость, в которой лежит экватор).

? 9. Выразите радиус rгс геостационарной орбиты через ускорение свободного падения g вблизи поверхности Земли, радиус Земли и продолжительность суток T.

Подсказка. Запишите уравнение второго закона Ньютона для спутника связи, выразив в нем гравитационную постоянную G через g, MЗем, Rзем.

? 10. Чему равен радиус геостационарной орбиты? На какой высоте над поверхностью Земли находится эта орбита?

Выполнив это задание, вы оцените уровень современной техники: спутниковая антенна устойчиво принимает сигнал с расстояния в десятки тысяч километров!

Вес тела на полюсе и на экваторе

Вследствие вращения планеты вокруг своей оси (его называют суточным) вес одного и того же тела на экваторе планеты меньше, чем на ее полюсе. Выясним, от чего зависит разность значений веса на экваторе и на полюсе.

Пусть тело покоится на поверхности шарообразной планеты вблизи ее полюса. В этом случае вес тела

где g – ускорение свободного падения.

Чтобы найти вес тела на поверхности планеты вблизи экватора, надо учесть суточное вращение планеты.

Вследствие этого вращения находящееся на экваторе тело равномерно движется по окружности относительно инерциальной системы отсчета, связанной с удаленными звездами (рис. 18.3). Радиус окружности равен радиусу планеты R, а период обращения T равен продолжительности суток.

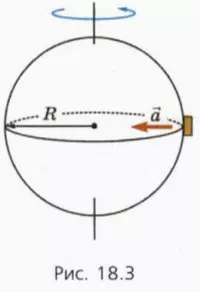
Вследствие суточного вращения планеты находящееся на ее экваторе тело движется относительно инерциальная центростремительным ускорением

Это ускорение направлено к центру планеты, то есть вниз. А если тело движется с ускорением , направленным вниз, вес этого тела выражается формулой (см. § 16):

? 11. Чему равно уменьшение веса тела массой m на экваторе шарообразной планеты радиусом R по сравнению с его весом на полюсе, если период обращения планеты равен T?

? 12. С помощью каких весов можно обнаружить уменьшение веса тела на экваторе – рычажных, в которых используются гири, или пружинных, когда вес тела измеряют по удлинению пружины?

? 13. Каково обусловленное суточным вращением Земли уменьшение веса корабля массой 40000 т при переходе его из приполярной области в экваториальные воды? Уменьшается ли при этом масса корабля?

? 14. На сколько процентов уменьшается вес тела вследствие суточного вращения Земли при перемещении его с полюса Земли на экватор?

Существует еще одна причина уменьшения веса тела на экваторе Земли по сравнению с весом на полюсе.

Дело в том, что Земля немного сплюснута у полюсов – расстояние между Северным и Южным полюсами (по прямой сквозь Землю) примерно на 43 км меньше, чем расстояние между диаметрально противоположными точками экватора Земли. Вследствие этого на полюсе находящаяся на уровне моря точка расположена примерно на 21,5 км ближе к центру Земли, чем точка на экваторе.

Общее уменьшение веса, обусловленное суточным вращением и сплюснутостью Земли, составляет примерно 0,5 %.

? 15. Каким должен быть период обращения шарообразной планеты массой M и радиусом r вокруг своей оси, чтобы находящиеся на ее экваторе тела находились в состоянии невесомости?

? 16. При какой продолжительности земных суток тела на земном экваторе были бы в состоянии невесомости?

Дополнительные вопросы и задания

17. Сорвавшийся с обрыва на некоторой планете камень падал с высоты h в течение времени t. Радиус планеты равен R. Чему равна масса планеты M?

18. Высадившийся на планету радиусом R астронавт бросает камешки с начальной скоростью v₀ под разными углами к горизонту. Чему равна средняя плотность планеты, если все камешки упали на расстоянии от космонавта, не превышающем l?

19. Космонавты высадились на экваторе шарообразной малой планеты. Средняя плотность планеты ρ, радиус R, продолжительность суток T.
а) Чему равна скорость точек поверхности планеты на экваторе?
б) Чему равна первая космическая скорость для этой планеты?
в) С какой скоростью космонавты могут ехать на гусеничном вездеходе вдоль экватора по направлению суточного вращения планеты, не отрываясь от ее поверхности?

20. Над находящейся на экваторе Земли африканской деревней 2 раза в сутки – в полдень и в полночь – пролетают одновременно два искусственных спутника, А и Б. Орбиты спутников лежат в экваториальной плоскости, спутник А движется на восток, а Б – на запад.
а) Какой спутник движется в направлении суточного вращения Земли, а какой – в противоположном?
б) Чему равен период обращения каждого спутника?
в) Каковы радиусы орбит спутников?

21. Космический корабль массой 10 т должен постоянно находиться в точке, где силы притяжения со стороны Земли и Луны уравновешивают друг друга. Примите, что Землю можно считать неподвижной, а расстояние от Земли до Луны постоянным.
а) Как направлена сила тяги двигателя корабля?
б) Выразите расстояние r от Земли до корабля через массу Земли M_Зем массу Луны M_Л и расстояние R_ЗЛ от Земли до Луны.
в) Чему равна сила тяги двигателя корабля?

Источник

Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше

Условие задачи:

Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше, чем на экваторе. Период вращения планеты вокруг своей оси 2 ч 40 мин.

Задача №2.5.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Тело на экваторе вращается вместе с планетой по окружности радиуса (R) (радиус планеты). Применим второй закон Ньютона:

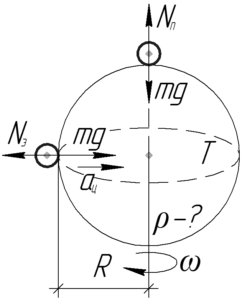
Тело на полюсе лежит на оси вращения планеты, поэтому оно вращается лишь вокруг себя. Первый закон Ньютона для этого тела даст такое равенство:

По третьему закону Ньютона сила реакции опоры ((N_э) и (N_п)) равна весу тела ((P_э) и (P_п) соответственно). Учтите, что эти силы хоть и равны по величине, но противоположны по направлению и приложены к разным телам. С учетом этого запишем равенства (1) и (2) в такой системе:

Поделим нижнее равенство на верхнее. Так как (P_п=2P_э), то получим:

Поскольку в задаче нужно узнать среднюю плотность планеты (rho), то запишем такие формулы: во-первых, формулу определения ускорения свободного падения (g) на поверхности планеты, во-вторых, формулу определения массы через плотность и объем, в-третьих, формулу определения объема шара.

Подставив (6) в (5), а полученное в (4), получим:

Чтобы выразить центростремительное ускорение (a_ц) через период вращения планеты (T) запишем такие формулы: формулу определения ускорения (a_ц) через угловую скорость (omega) и формулу связи последней с периодом вращения (T).

Подставим выражения (7) и (8) в ранее полученное равенство (3):

Переведем данный в условии период вращения (T) в систему СИ (в секунды):

[T = 2;ч;40;мин = 2 cdot 3600 + 40 cdot 60; с = 9600; с]

Ответ: 3,07 г/см 3 .

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Источник

Условие задачи:

Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше, чем на экваторе. Период вращения планеты вокруг своей оси 2 ч 40 мин.

Задача №2.5.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(P_п=2P_э), (T=2; ч; 40; мин), (rho-?)

Решение задачи:

Тело на экваторе вращается вместе с планетой по окружности радиуса (R) (радиус планеты). Применим второй закон Ньютона:

[mg – {N_э} = m{a_ц};;;;(1)]

Тело на полюсе лежит на оси вращения планеты, поэтому оно вращается лишь вокруг себя. Первый закон Ньютона для этого тела даст такое равенство:

[mg = {N_п};;;;(2)]

По третьему закону Ньютона сила реакции опоры ((N_э) и (N_п)) равна весу тела ((P_э) и (P_п) соответственно). Учтите, что эти силы хоть и равны по величине, но противоположны по направлению и приложены к разным телам. С учетом этого запишем равенства (1) и (2) в такой системе:

[left{ begin{gathered}
{P_э} = mg – m{a_ц} hfill \
{P_п} = mg hfill \
end{gathered} right.]

Поделим нижнее равенство на верхнее. Так как (P_п=2P_э), то получим:

[frac{g}{{g – {a_ц}}} = 2]

[2g – 2{a_ц} = g]

[g = 2{a_ц};;;;(3)]

Поскольку в задаче нужно узнать среднюю плотность планеты (rho), то запишем такие формулы: во-первых, формулу определения ускорения свободного падения (g) на поверхности планеты, во-вторых, формулу определения массы через плотность и объем, в-третьих, формулу определения объема шара.

[g = Gfrac{M}{{{R^2}}};;;;(4)]

[M = rho  cdot V;;;;(5)]

[V = frac{4}{3}pi {R^3};;;;(6)]

Подставив (6) в (5), а полученное в (4), получим:

[g = frac{4}{3}pi Grho R;;;;(7)]

Чтобы выразить центростремительное ускорение (a_ц) через период вращения планеты (T) запишем такие формулы: формулу определения ускорения (a_ц) через угловую скорость (omega) и формулу связи последней с периодом вращения (T).

[{a_ц} = {omega ^2}R]

[omega  = frac{{2pi }}{T}]

В итоге:

[{a_ц} = frac{{4{pi ^2}}}{{{T^2}}}R;;;;(8)]

Подставим выражения (7) и (8) в ранее полученное равенство (3):

[frac{4}{3}pi Grho R = frac{{8{pi ^2}}}{{{T^2}}}R]

[rho  = frac{{6pi }}{{G{T^2}}}]

Переведем данный в условии период вращения (T) в систему СИ (в секунды):

[T = 2;ч;40;мин = 2 cdot 3600 + 40 cdot 60; с = 9600; с]

Посчитаем ответ:

[rho  = frac{{6 cdot 3,14}}{{6,67 cdot {{10}^{ – 11}} cdot {{9600}^2}}} = 3065; кг/м^3 approx 3,07; г/см^3]

Ответ: 3,07 г/см³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.14 Во сколько раз период обращения искусственного спутника, совершающего движение
2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

2. Чему равна плотность планеты, если период обращения вокруг нее спутника, движущегося на небольшой высоте, равен Т?

Задача из главы Механика. Динамика периодического движения по предмету Физика из задачника Физика, Касьянов (10 класс)

Если к данной задачи нет решения — не переживайте. Наши администраторы стараются дополнять сайт решениями для тех задач
и упражнения где это требуется и которые не даны в решебниках и сборниках с ГДЗ. Попробуйте зайти позже. Вероятно, вы найдете то, что искали

5. Динамика периодического движения. §37. Движение тел в гравитационном поле. Задачи → номер 2

2.

Решение:

Ответ: