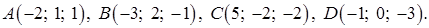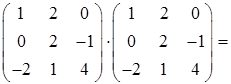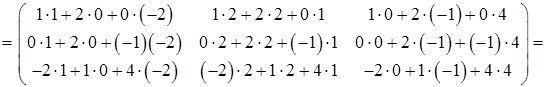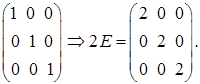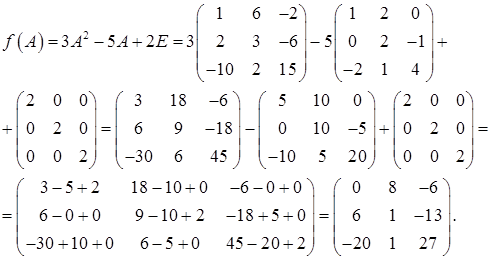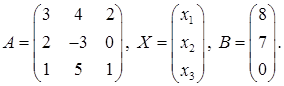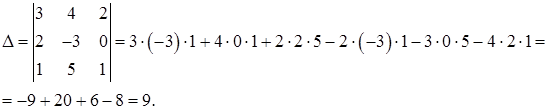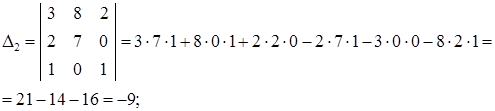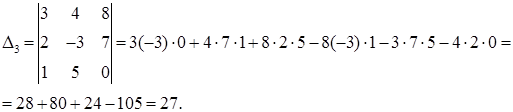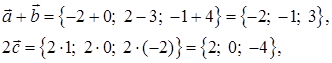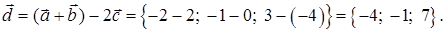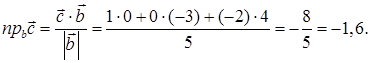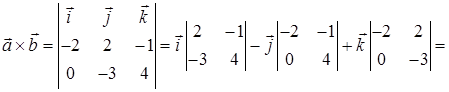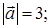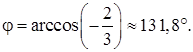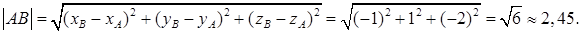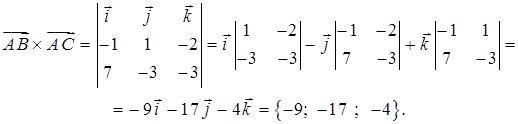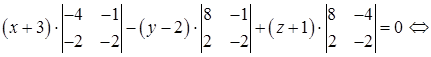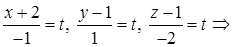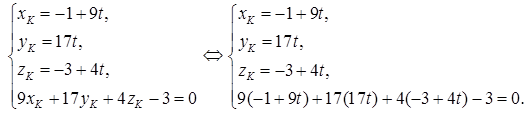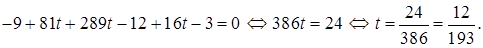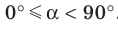Объяснение:
№3
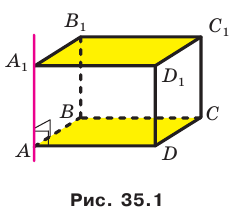
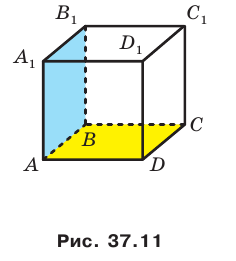
1а) рёбра перпендикулярные плоскости (ДСС1):
В1С1, А1Д1, ВС, АД
2а) плоскости перпендикулярные ребру ВВ1:
АВС и А1В1С1
1б) прямая СС1 перпендикулярна к плоскости (ДСВ)
2б) прямая Д1С1 параллельна плоскости (ДСВ)
№4
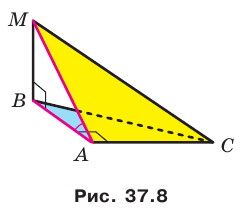
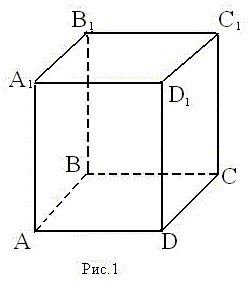
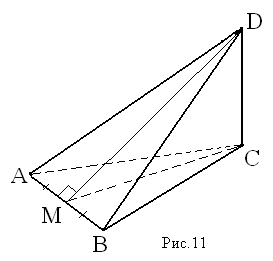
1) АС перпендикулярно АВ (∠А=90°)
2) АС перпендикулярна АМ, (по условию)
тогда АС перпендикулярна плоскости АМВ, поскольку она перпендикулярна двум прямым в этой плоскости: АВ и АМ
ДОКАЗАНО
Геометрия, 10 класс
Урок №11. Перпендикулярность плоскостей
Перечень вопросов, рассматриваемых в теме.
- Свойства двугранного угла;
- Доказательство признака перпендикулярности двух плоскостей;
- Свойства прямоугольного параллелепипеда.
Глоссарий по теме
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Перпендикуляры к ребру двугранного угла образуют линейный угол двугранного угла. Градусной мерой двугранного угла называется градусная мера его линейного угла.
Если угол между пересекающимися плоскостями равен 90 градусом, то плоскости перпендикулярны.
Признак перпендикулярности плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Следствие из признака перпендикулярности плоскостей: Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Прямоугольный параллелепипед – фигура, у которой все боковые ребра перпендикулярны основанию.
Основная литература:
Атанасян Л.С., Бутузов В.Ф. Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Дополнительная литература:
Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. Прямая а, которая является общей границей полуплоскостей, называется ребром двугранного угла (рис. 1а и 1б).
Двугранный угол с ребром CD, на разных гранях которого отмечены точки A и B называют двугранным углом CABD.
Перпендикуляры к ребру AO и BO образуют линейный угол двугранного угла AOB (рис. 1в). Так как луч ОА перпендикулярен прямой CD и луч OB перпендикулярен прямой CD, то плоскость АОВ перпендикулярна к прямой CD. Таким образом, плоскость линейного угла перпендикулярна к ребру двугранного угла. Двугранный угол имеет бесконечное множество линейных углов
Градусной мерой двугранного угла называется градусная мера его линейного угла. Так же как и плоские углы, двугранные углы могут быть прямыми, острыми и тупыми.
Все линейные углы двугранного угла равны друг другу.
Рассмотрим два линейных угла АОВ и А1О1В1 (рис. 1г). Лучи ОА и О1А1, лежат в одной грани и перпендикулярны к прямой ОО1, поэтому они сонаправлены. Точно так же сонаправлены лучи OB и O1B1. Поэтому углы АОВ и А1О1В1 равны как углы с сонаправленными сторонами.
(Рис. 1)
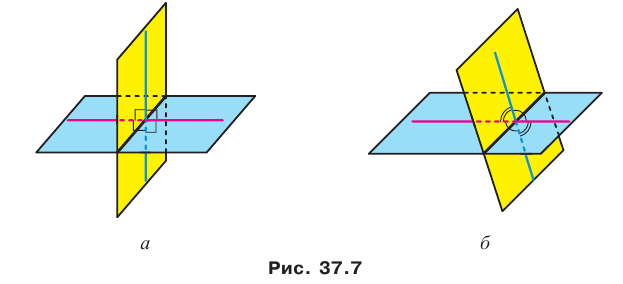
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.
Если один из этих двугранных углов равен фи, то другие три угла равны соответственно 180 градусов минус фи, фи и 180 градусов минус фи (рис. 2 а). В частности, если один из углов прямой, то и остальные три угла прямые. Если угол между пересекающимися плоскостями равен 90 градусом, будем называть такие плоскости перпендикулярными (рис. 2б).
(Рис. 2)
Для доказательства теоремы рассмотрим плоскости альфа и бетта такие (рис. 3), что плоскость альфа проходит через прямую АВ, перпендикулярную к плоскости бетта и пересекающуюся с ней в точке А. Докажем, что плоскости альфа и бетта перпендикулярны. Плоскости альфа и бетта пересекаются по некоторой прямой АС. При этом прямая АВ перпендикулярна прямой АС, так как по условию прямая АВ перпендикулярна плоскости бетта, это означает, что прямая АВ перпендикулярна к любой прямой, лежащей в плоскости бетта.
Проведем в плоскости бетта прямую AD, перпендикулярную к прямой АС. Тогда угол BAD — линейный угол двугранного угла, образованного при пересечении плоскостей альфа и бетта. Но угол BAD равен 90 градусов так как прямая АВ перпендикулярна плоскости бетта. Следовательно, угол между плоскостями альфа и бетта равен 90 градусов. Что и требовалось доказать.
(Рис. 3)
Из этой теоремы вытекает важное следствие:
Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
|
На рисунке 4 представлен прямоугольный параллелепипед. У этой фигуры все боковые ребра перпендикулярны основанию. Его основаниями служат прямоугольники ABCD и A1B1C1D1, а боковые ребра АА1,BB1,CC1 и DD1 перпендикулярны к основаниям. Отсюда следует, что ребро АА1 перпендикулярно к ребру АВ, т. е. боковая грань АА1В1В является прямоугольником. То же самое можно сказать и об остальных боковых гранях. |
|
Таким образом, прямоугольный параллелепипед обладает следующими свойствами: 1) В прямоугольном параллелепипеде все шесть граней — прямоугольники. 2) Все двугранные углы прямоугольного параллелепипеда — прямые. 3) Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Измерениями прямоугольного параллелепипеда называются длины трех ребер, имеющих общую вершину. Докажем последнее свойство. |
(Рис. 4)
Так как ребро СС1 перпендикулярно к основанию ABCD, то угол АСС1, прямой. Из прямоугольного треугольника АСС1, по теореме Пифагора получаем
АС12 равно АС2 +СС12.
Но АС — диагональ прямоугольника ABCD, поэтому АС2 равно АВ2 + АD2. Кроме того, ребро СС1 равно ребру АА1. Следовательно, AC1 равно АВ2 + AD2 + АА12. Что и требовалось доказать.
Следствием из этого свойства является то, что диагонали прямоугольного параллелепипеда равны.
Стоит отметить, что если у прямоугольного параллелепипеда все три измерения равны, то он называется, а все его грани являются равными друг другу квадратами.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. В прямоугольном параллелепипеде ABCDA1B1C1D1 (рис. 5) боковая грань DD1C1C – квадрат, DC равно 4 см, BD1 равно 6 см. Найдите BC и докажите, что плоскости BCD1 и DC1 B1 взаимно перпендикулярны.
Сначала найдем BC. Воспользуемся тем свойством прямоугольного параллелепипеда, что квадрат его диагонали равен сумме квадратов трех его измерений.
Тогда диагональ BD1 в квадрате равна AD в квадрате плюс DD1 в квадрате плюс DC в квадрате. BD1 – известно из условия, DD1 и DC – стороны квадрата и тоже известны из условия, тогда отсюда мы можем выразить ребро AD, которое ребру BC.Отсюда находим, что BC равно 2 сантиметрам.
Для доказательства перпендикулярности плоскостей BCD1 и DC1 B1 воспользуемся признаком перпендикулярности плоскостей. Этот признак звучит следующим образом: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Заметим, что плоскость BCD1 проходит через диагональ грани DD1 C1C – CD1. Эта диагональ перпендикулярна плоскости DC1 B1 в соответствии с признаком перпендикулярности прямой и плоскости, так как CD1 перпендикулярна второй диагонали квадрата – C1D и перпендикулярна ребру прямоугольного параллелепипеда C1 B1. Что и требовалось доказать.
(Рис. 5)
Тестовый вопрос №2. В прямом двугранном угле дана точка A. Расстояния от точки A до граней угла: AA1=6 см и AB1=8 см. Определите расстояние от точки A до ребра двухгранного угла.
Решение.
Отрезки AA1 и AB1 перпендикулярны граням двугранного угла, поэтому AA1BB1 – прямоугольник. Искомое расстояние – диагональ этого прямоугольника, которую найдем с помощью теоремы Пифагора: сантиметров.
Ответ: 10 см.
Тестовый вопрос №10. В прямоугольном параллелепипеде ABCDA1B1C1D1 длины рёбер: AB = 2, BC=3, AA1 = 4. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C1.
Решение. Нарисуем рисунок.
В рассматриваемом прямоугольном параллелепипеде проведем отрезок BC1. Затем построим плоскость на прямых BC1 и AB. Так как плоскости прямоугольного параллелепипеда AA1D1D и BB1C1C параллельны, поэтому искомым сечением является прямоугольник ABC1D1.
Нам известны отрезки AA1 и BC, из них по теореме Пифагора вычислим длину отрезка BC1: .
Теперь найдем площадь искомого прямоугольника: 10 .
Ответ: 10.
Уравнение плоскости в пространстве
Общее уравнение плоскости: 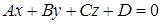
где A, B, C – координаты вектора нормали вектора 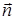
Уравнение плоскости, проходящей через точку 


Уравнение плоскости, проходящей через три заданные точки
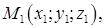

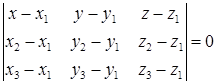
Угол 
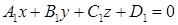


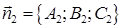
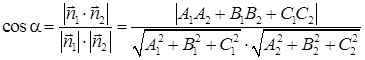
Уравнения прямой в пространстве
Параметрические уравнения прямой l в пространстве:
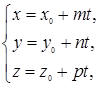
где 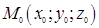
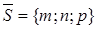
Каждому значению параметра 
Канонические уравнения прямой:

Уравнения прямой, проходящей через две данные точки 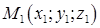
и 

Углом 
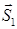


Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла 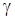
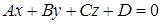

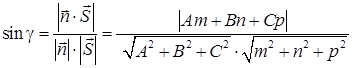
Примерный вариант и образец выполнения
контрольной работы № 2
Задача 1. Даны многочлен f(x) и матрица А:
Требуется найти значение матричного многочлена f (A).
Задача 2. Дана система трех линейных алгебраических уравнений
с тремя неизвестными:
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 3. Даны координаты трех векторов: 



1) вычислить модуль вектора 
2) найти координаты вектора 
3) найти угол φ между векторами 
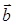
4) вычислить проекцию вектора 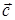
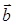
5) вычислить площадь треугольника, построенного на векторах 
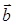
6) вычислить объем параллелепипеда, построенного на векторах 
Задача 4. Даны координаты точек – вершин пирамиды ABCD:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол 
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол 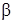


9) сделать чертеж пирамиды в системе координат.
Решение задачи 1
Записываем матричный многочлен: 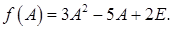
Найдем матрицу A 2 . При умножении матрицы A на себя используем правило «строка на столбец» (формула (23)):
A 2 = A·A =
Найдем матрицу 2Е, используя правило умножения матрицы на число (формула (21)):
E =
Теперь найдем значение матричного многочлена f(A),используя правило умножения матрицы на число и правило сложения матриц (формула (22)):
Ответ:
Решение задачи 2
1) Запишем систему в матричном виде:
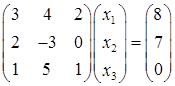
где
(Во втором уравнении системы отсутствует неизвестная х3, т. е. а23 = 0).
2) Решим систему с помощью формул Крамера. Для этого по формулам (29) составляем главный определитель системы из коэффициентов при неизвестных в левых частях уравнений и три вспомогательных определителя:
Вычислим эти определители, используя формулу (25):
Так как ∆ ≠ 0, то данная система имеет единственное решение.
Найдем решение системы по формулам Крамера (30):
3) Решим систему при помощи обратной матрицы.
a) Определитель 
б) Чтобы найти союзную матрицу 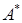
Здесь определители 2-го порядка вычислены по формуле (24).
Тогда союзная матрица (см. формулу (31)):
в) Найдем обратную матрицу по формуле (32):
г) Получим решение системы при помощи обратной матрицы по формуле (33) (правило «строка на столбец»):
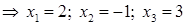
Решение, полученное матричным способом, совпадает с тем, которое получено по формулам Крамера, что подтверждает правильность этого решения.
1) система в матричном виде: AX = B, где
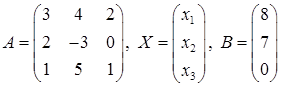
2) решение системы, полученное с помощью формул Крамера:

3) решение системы, полученное при помощи обратной матрицы:

Решение задачи 3
1) Модуль вектора 
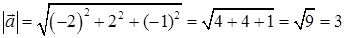
2) Чтобы найти координаты вектора 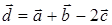
тогда
3) Косинус угла между векторами 
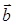
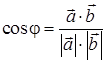
Для этого вычислим скалярное произведение 
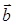

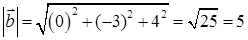

и
4) Проекцию вектора 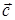
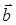
5) Площадь треугольника, построенного на векторах 
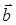
Следовательно, площадь треугольника, построенного на векторах 
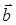
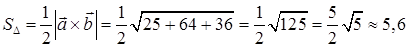
6) Для вычисления объема параллелепипеда, построенного на векторах 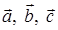
тогда объема параллелепипеда по формуле (47): 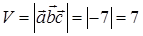
1) модуль вектора 
2) координаты вектора 
3) угол между векторами 
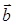
4) проекция вектора 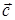
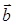
5) площадь треугольника, построенного на векторах 
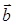
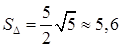
6) объем параллелепипеда, построенного на векторах 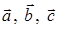
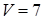
Решение задачи 4
1) Длину ребра 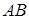
2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т. е. вектор, перпендикулярный векторам 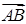
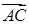
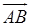
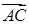
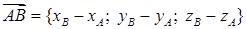
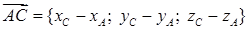
Векторное произведение 
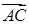
В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, 
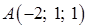
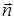



3) Прежде, чем найти угол 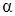
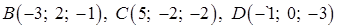
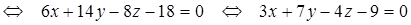
Из уравнения плоскости BCD возьмем координаты вектора нормали 

Косинус угла 
по формуле(50):
Отсюда 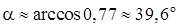
4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A(–2; 1; 1) и имеющей направляющий вектор 
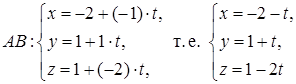
Другой способ: можно использовать уравнения прямой, проходящей через две точки 
откуда, обозначив каждую из дробей t, получаем:

5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор 
и вектор 

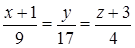
6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK. Обозначив каждую из дробей
в канонических уравнениях буквой t, получаем:
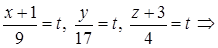

Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты 
Решим последнее уравнение относительно t:
Вычислим координаты точки K, подставив найденное значение параметра в первые три уравнения системы:
Итак, точка пересечения DK и грани ABC: 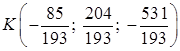
7) Угол 
правляющими векторами прямых AB и BC: 
и 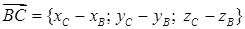

по формуле(54):
Тогда угол между ребрами AB и BC:


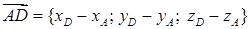
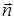
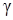
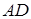
Тогда угол между ребром AD и гранью ABC:
9) Выполним чертеж пирамиды в системе координат (рис. 19).
1)
2) АВС:
3) 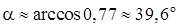
4)
5) DK: 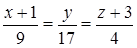
6) 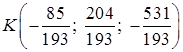
7) 


9) чертеж пирамиды на рис. 19.
Варианты контрольнЫХ работ
Каждый вариант контрольной работы № 1 для студентов-заочников
1 курса всех специальностей содержит 5 задач, охватывающих материал по теме «Аналитическая геометрия на плоскости». Каждый вариант контрольной работы № 2 содержит 4 задачи по темам «Элементы линейной алгебры. Аналитическая геометрия в пространстве».
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Варианты контрольной работы № 1
Задача 1. Даны координаты вершин треугольника АВС.
| Номер варианта | Координаты точек | Номер варианта | Координаты точек |
| А(–2; –3), В(2; 7), С(6; –1) | А(3; –3), В(–4; 1), С(–2; 5) | ||
| А(–5; 1), В(6; 3), С(–4; –7) | А(3; 5), В(–2; 2), С(2; –4) | ||
| А(4; 5), В(–3; 2), С(5; –4) | А(–2; 4), В(5; 6), С(3; –4) | ||
| А(7; –7), В(1; 2), С(–5; –4) | А(3; 7), В(–4; 1), С(–2; –5) | ||
| А(–3; 4), В(4; 5), С(8; –3) | А(4; 3), В(–3; –2), С(–7; 2) |
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точки А, уравнение прямой l и число λ.
| Номер варианта | Координаты точки | Уравнение прямой l | Число λ | Номер варианта | Координаты точки | Уравнение прямой l | Число λ |
| А(–1; 0) | y + 2 = 0 | 1 : 1 | А(–5; 1) | x + 1 = 0 | 1: 1 | ||
| А(3; 1) | 3x = 16 | 3 : 4 | А(5; –4) | 5x = 1 | 5 : 1 | ||
| А(3; 0) | x = 0 | 2 : 1 | А(1; 0) | 2x = 7 | 2 : 3 | ||
| А(2; 0) | 4x = 1 | 4 : 3 | А(1; 2) | x = 4 | 1 : 2 | ||
| А(0; 0) | 2x + 5 = 0 | 2 : 3 | А(3; 2) | 3x = 1 | 3 : 1 |
Найти уравнение траектории точки М, которая движется в плоскости так, что отношение ее расстояний до точки А и до прямой l равно λ. Сделать чертеж в системе координат.
Задача 3. Дано уравнение кривой 2-го порядка.
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
| 7x 2 – 9y 2 + 42x+ 18y – 9 = 0 | 9x 2 + 4y 2 – 54x + 8y + 49 = 0 | ||
| x 2 + 2x – 12y + 37 = 0 | x 2 – 10x + 4y + 17 = 0 | ||
| 5x 2 + 9y 2 + 10x – 54y + 41 = 0 | 3x 2 – y 2 – 30x – 2y + 62 = 0 | ||
| y 2 + 6x + 6y – 3 = 0 | y 2 – 8x – 4y – 4 = 0 | ||
| 5x 2 – 4y 2 – 20x – 24y – 36 = 0 | 7x 2 + 16y 2 – 56x + 64y + 64 = 0 |
Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.
Задача 4. Даны уравнение кривой 2-го порядка и уравнение прямой.
| Номер варианта | Уравнение кривой | Уравнение прямой |
| x 2 + 2y 2 – 2x + 8y + 3 = 0 | x + 2y + 3 = 0 | |
| x 2 – 2y 2 + 4x + 4y – 6 = 0 | x + 2y = 0 | |
| x 2 + 6x – 16y + 25 = 0 | x – 4y + 15 = 0 | |
| x 2 + 4y 2 – 6x + 8y + 5 = 0 | x – 2y – 5 = 0 | |
| y 2 – 4x – 6y – 15 = 0 | 2x + y – 3 = 0 | |
| x 2 – 5y 2 + 10x + 20y – 15 = 0 | x – 5y + 15 = 0 | |
| x 2 + 4y 2 + 2x – 32y + 45 = 0 | x – y + 5 = 0 | |
| x 2 – 4x + 8y + 44 = 0 | x – 2y – 20 = 0 | |
| 2x 2 – y 2 – 16x – 6y + 19 = 0 | x – y – 7 = 0 | |
| y 2 + 10x + 8y – 34 = 0 | 2x + y + 4 = 0 |
1) привести заданное уравнение кривой 2-го порядка к каноническому виду;
2) найти точки пересечения кривой и заданной прямой;
3) построить обе линии в исходной системе координат.
Задача 5. Дано уравнение кривой в полярной системе координат (ПСК).
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
 |
 |
||
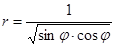 |
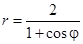 |
||
 |
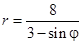 |
||
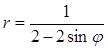 |
 |
||
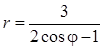 |
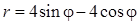 |
1) найти область определения функции 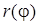
2) построить кривую в ПСК, вычислив значения функции в точках 

3) найти уравнение заданной кривой в декартовой системе координат (ДСК), начало координат в которой совпадает с полюсом ПСК, а положительная полуось ОХ – с полярной осью ОР;
4) определить тип кривой.
Варианты контрольной работы № 2
Задача 1. Даны многочлен f(x) и матрица А.
| Номер варианта | Многочлен f(x) | Матрица А |
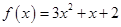 |
 |
|
 |
 |
|
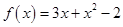 |
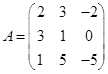 |
|
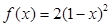 |
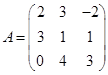 |
|
 |
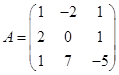 |
|
 |
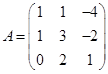 |
|
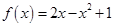 |
 |
|
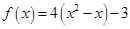 |
 |
Требуется найти значение матричного многочлена 
Задача 2. Дана система трех линейных алгебраических уравнений
с тремя неизвестными.
| Номер варианта | Система уравнений | Номер варианта | Система уравнений |
 |
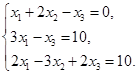 |
||
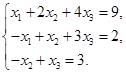 |
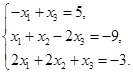 |
||
 |
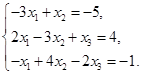 |
||
 |
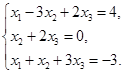 |
||
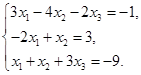 |
 |
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 3. Даны координаты трех векторов 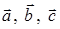

| Номер варианта | Векторы  |
Вектор  |
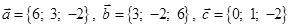 |
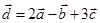 |
|
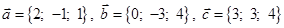 |
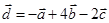 |
|
 |
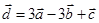 |
| Номер варианта | Векторы 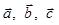 |
Вектор 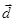 |
 |
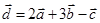 |
|
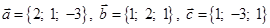 |
 |
|
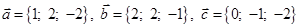 |
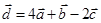 |
|
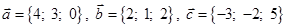 |
 |
|
 |
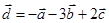 |
|
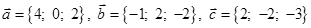 |
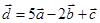 |
|
 |
 |
1) вычислить модуль вектора 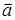
2) найти координаты вектора 
3) найти угол φ между векторами 
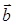
4) вычислить проекцию вектора 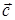
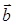
5) вычислить площадь треугольника, построенного на векторах 
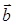
6) вычислить объем параллелепипеда, построенного на векторах 
Задача 4. Даны координаты точек – вершин пирамиды ABCD.
| Номер варианта | Координаты точек |
| А(1; 2; –1), В(0; 0; 1), С(1; –3; 3), D(2; –1; –1) | |
| А(7; 2; 4), В(7; –1; –2), С(3; 3; 1), D(4; 2; 1) | |
| А(1; 3; 6), В(2; 2; 1), С(–1; 0; 1), D(–4; 6; –3) | |
| А(–2; 0; –4), В(–1; 7; 1), С(4; –8; –4), D(1; –4; 6) | |
| А(1; 2; 0), В(3; 0; –1), С(5; –2; 3), D(3; 2; –1) | |
| А(–1; 1; 2), В(2; 1; –2), С(–2; 0; 4), D(2; –1; 2) | |
| А(4; 2; 5), В(2; –3; 0), С(–10; 5; 8), D(–5; 2; 4) | |
| А(2; –1; 1), В(–1; –3; 2), С(–2; 3; 1), D(–1; 2; –3) | |
| А(–1; 1; 2), В(–2; 0; 3), С(3; 6; –3), D(–1; –2; 7) | |
| А(4; –1; 3), В(–2; 1; 0), С(0; –5; 1), D(–2; 1; –1) |
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол 
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол 


9) сделать чертеж пирамиды в системе координат.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – М. : Айрис-пресс, 2003. – 288 с.
2. Щипачев, В.С. Высшая математика : учебник для вузов / В.С. Щипачев.– М. : Высш. шк., 1998. – 479 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999. – 304 с.
4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев. – М. : Высш. шк., 2001. – 304 с.
Налоговая льгота – Общероссийский классификатор продукции
ОК 005-93, т. 2; 95 3004 – воспитательная, образовательная и педагогическая литература
Издательство МГТУ. 183010 Мурманск, Спортивная, 13.
Сдано в набор 14.09.2007. Подписано в печать 18.09.2007. Формат 60´84 1 /16.
Бум. типографская. Усл. печ. л. 2,79. Уч.-изд. л. 2,18. Заказ 443. Тираж 300 экз.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
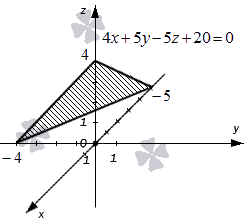
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Общее уравнение плоскости : описание, примеры, решение задачВ статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости. Общее уравнение плоскости: основные сведенияПеред началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным. Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости. Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю. Теорема состоит из двух частей. Разберем доказательство каждой из них.
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю: n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 ) Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость. Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью. Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства. Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства. Раскроем чуть шире смысл теорем. В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат. Укажем пример как иллюстрацию этих утверждений. Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость. Общее уравнение плоскости, проходящей через точкуПовторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество. Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости. Решение Подставим координаты точки М 0 в исходной уравнение плоскости: 2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0 Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости. Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение: 2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0 Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости. Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит. Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости. В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости. Решение Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так: λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0 Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0 Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора. Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали. Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0 Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) . Возможно получить это уравнение другим способом. Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю: n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости. Решение Рассмотрим два способа решения.
x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5 Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0
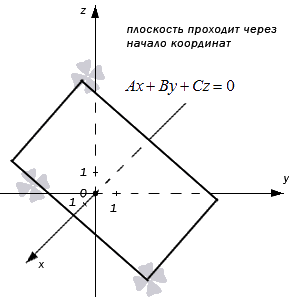
M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 ) Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда: n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0 Ответ: 3 x + 7 y — 5 z — 26 = 0 Неполное общее уравнение плоскостиВыше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным. Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству: A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0 Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости. Решение Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 . Задачу возможно решить еще одним способом. Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости: A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0 Ответ: x — 7 = 0 Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) . Решение Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 . Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 . Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 . источники: http://mathhelpplanet.com/static.php?p=onlayn-resheniye-piramidy http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-ploskosti/ |
Содержание:
Перпендикулярность в пространстве
В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свойство ортогональной проекции многоугольника.
Угол между прямыми в пространстве
Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 
Угол между двумя параллельными прямыми считают равным 
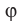
Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Пусть прямые 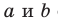
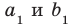
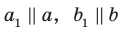
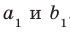
Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми 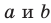
Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.
Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми 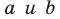
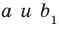
Например, на рисунке 33.3 изображена треугольная призма 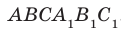
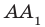
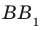
Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.
Если прямые 
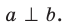
Например, ребра AD и 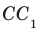
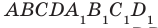
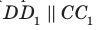
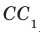
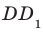
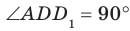
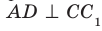
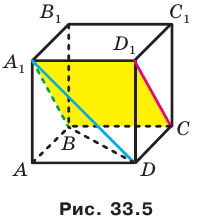
Пример:
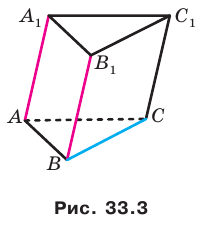
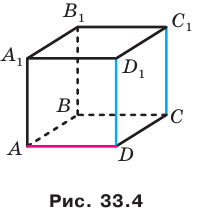
На рисунке 33.5 изображен куб 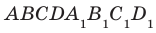
Решение:
Соединим точки 
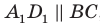
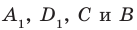
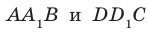
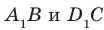
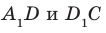
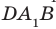
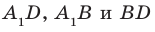
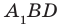
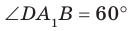
Перпендикулярность прямой и плоскости
В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.


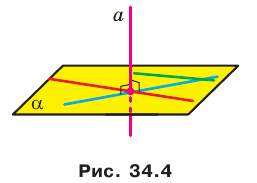
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).
Если прямая 
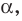
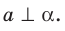
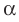
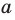
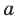
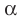
Из определения следует, что если прямая 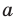
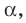
Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.
Например, интуитивно понятно, что ребро 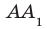
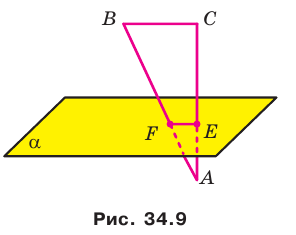
Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
На рисунке 34.5 прямая 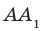
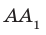
Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).
Приведем теорему, которую можно рассматривать как еще один признак перпендикулярности прямой и плоскости.
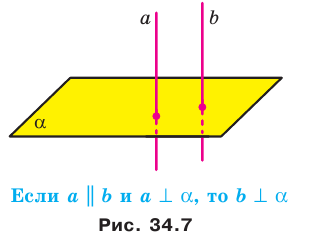
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).
Например, на рисунке 34.5 прямая 
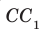
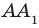
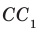
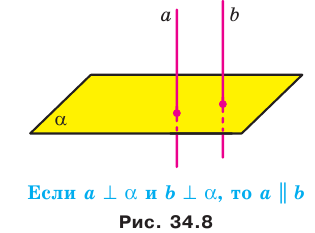
Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.
Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
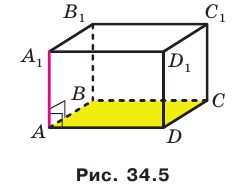
Пример:
Плоскость 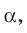
Решение:
Поскольку прямая АС перпендикулярна плоскости 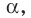
Перпендикуляр и наклонная
Пусть фигура 
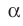
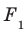
Например, основание ABCD прямоугольного параллелепипеда 
В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.
Пусть даны плоскость 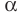
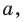
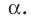
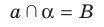
Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость 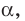
Отметим на плоскости 
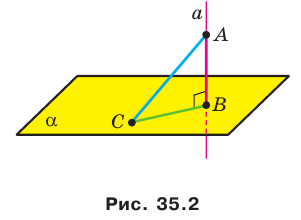
Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.
Пример:
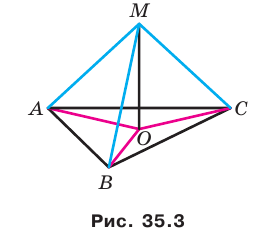
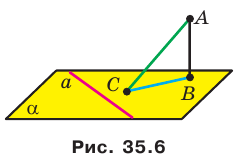
Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку 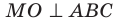
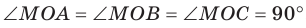
Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.
Определение. Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
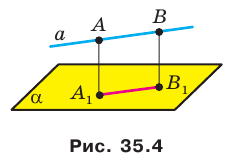
Пример:
Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.
Решение:
Пусть А и В — две произвольные точки прямой 
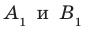
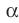
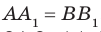
По теореме 34.3 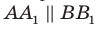
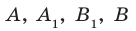
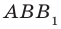
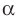
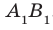
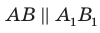
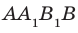
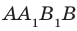
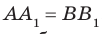
Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.
Пример:
Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Результаты, полученные в ключевых задачах 2 и 3, часто используют в практической деятельности, например в строительстве (рис. 35.5).

Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Доказательство. Докажем первую часть теоремы.Пусть прямая 
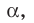
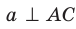
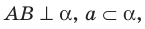
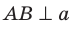
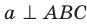
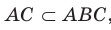
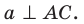
Пример:
Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.
Отрезок ON является проекцией наклонной MN на плоскость АВС. По построению 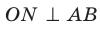
Аналогично можно доказать, что 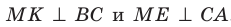
В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.
Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.
Угол между прямой и плоскостью
Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.
Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.
Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.
Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 
Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).
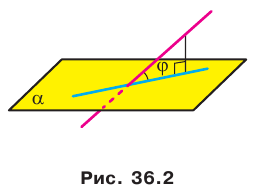
Из определения следует, что если 
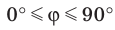
Также принято говорить, что прямая образует угол 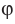
Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.
Например, рассмотрим куб 
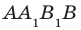
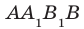
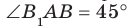
Пример:
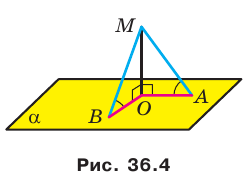
Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.
Решение:
Пусть МЛ и М В — наклонные, образующие с плоскостью 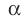
Прямая ОА является проекцией прямой МА на плоскость 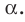
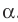
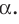
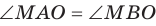
Поскольку 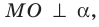
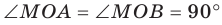
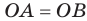
- Заказать решение задач по высшей математике
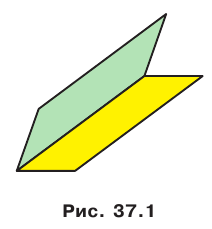
Двугранный угол. Угол между плоскостями
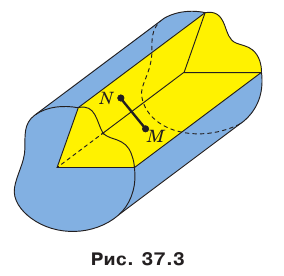
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугранным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).
Отрезок MN принадлежит «желтому» двугранному углу, а «синему» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).
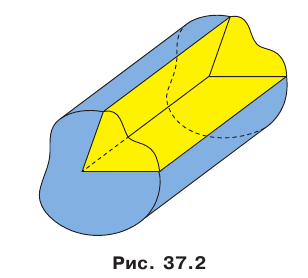
Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).
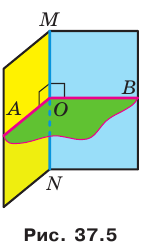
Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.
Отметим на ребре MN двугранного угла произвольную точку О. Через точку О в гранях двугранного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугранного угла. Поскольку 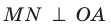
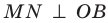
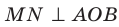
Определение. Величиной двугранного угла называют величину его линейного угла.
Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.
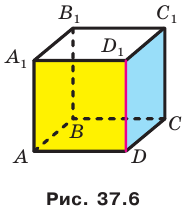
Например, рассмотрим куб 
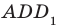
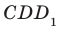
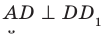
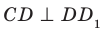
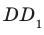
Угол ADC прямой.
При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:
- все четыре двугранных угла прямые (рис. 37.7, а);
- из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).
В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.
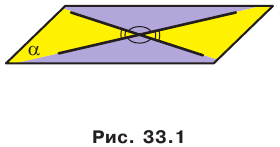
Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.
Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.
Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.
Пример:
Прямоугольные треугольники 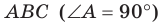
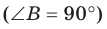
Решение:
Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как 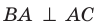
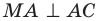
Для стороны AM прямоугольного треугольника АМС можно записать: 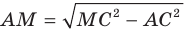
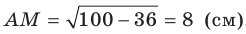
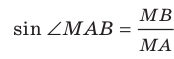
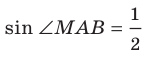
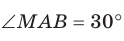
Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.
Теорема 37.1 (площадь ортогональной проекции многоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где 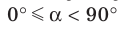
Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Если плоскости 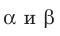
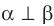
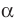
Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).
Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).
Теорема 37.2 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Например, плоскость грани 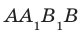
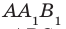
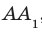

Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Перпендикулярность прямой и плоскости
- Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
- Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
- Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
- Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Ортогональная проекция фигуры
Пусть фигура 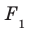
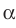
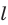
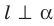
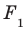
Расстояние от точки до плоскости
Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Расстояние от прямой до параллельной ей плоскости
Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями
Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Теорема о трех перпендикулярах
Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Угол между прямой и плоскостью
- Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
- Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
- Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.
Величина двугранного угла
Величиной двугранного угла называют величину его линейного угла.
Угол между двумя пересекающимися плоскостями
Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.
Площадь ортогональной проекции многоугольника
Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где
Перпендикулярные плоскости
Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Признак перпендикулярности плоскостей
Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Векторы и координаты в пространстве
- Множества
- Рациональные уравнения
- Рациональные неравенства и их системы
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
Цели:
- закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
- вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.
План:
- Теоретический опрос.
- Доказательство изученных теорем у доски.
- Фронтальный опрос.
- Презентации учащихся по данной теме.
- Решение задач.
- Решение устных задач по готовым чертежам.
- Решение письменных задач (по группам).
- Самостоятельная работа с индивидуальным заданием.
- Итог урока. Задание на дом.
Ход урока
I. Теоретический опрос (4 ученика у доски)
1) доказать лемму о 2-ух параллельных прямых, одна из которых перпендикулярна к третьей;
2) доказать теорему о 2-ух параллельных прямых, одна из которых перпендикулярна к плоскости;
3) доказать обратную теорему о параллельности 2-ух прямых, перпендикулярных к плоскости;
4) доказать признак перпендикулярности прямой и плоскости.
Пока ученики готовятся у доски к ответу, с классом проводится фронтальный опрос.
(С помощью мультимедиапроектора на экране появляются вопросы (Приложение 1), и ученики отвечают на них)
1. Закончить предложение:
а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)
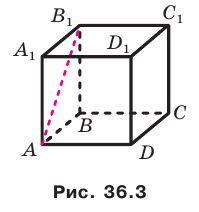
2. Дан параллелепипед
а) Назовите:
1) рёбра, перпендикулярные к плоскости (DCC1) (ответ: AD; A1D1; B1C1; BC)
2) плоскости, перпендикулярные ребру BB1 (ответ: (АВС); (A1B1C1))
б) Определите взаимное расположение:
1) прямой CC1 и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D1C1 и плоскости (DCB) (ответ: они параллельны)
Далее выслушиваются ответы учеников у доски с дополнениями и исправлениями по необходимости. Затем рассматриваются презентации по данной теме, подготовленные рядом учеников в качестве зачётных работ (Приложение 2, Приложение 3, Приложение 4).
(Накануне изучения каждой темы учащимся предлагается такой вариант зачёта)
II. Решение задач.
1. Решение задач по готовым чертежам (Устно)
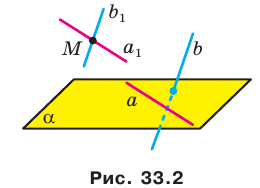
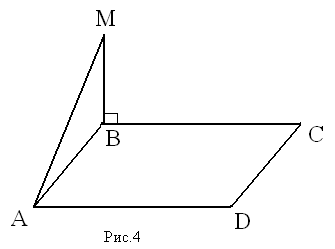
№1
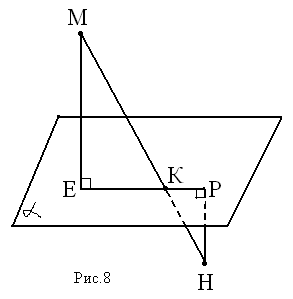
Дано: ∆ ABC — прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.
№2
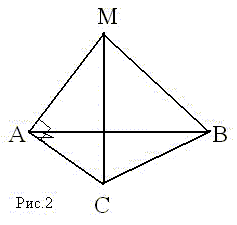
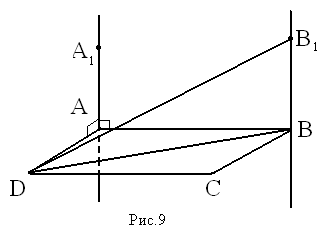
Дано: ВМDC — прямоугольник, M ∉ (ABC), MB ⊥ AB
Доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.
№3
Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.
№4
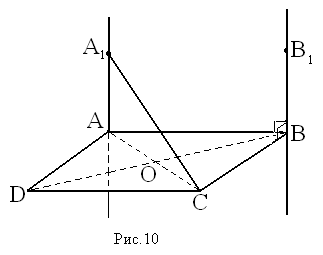
Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD — равнобедренный, т. к. ВМ = МD по условию, значит МО — медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.
(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)
2. Решение письменных задач
Класс делится на три группы (например, по рядам), и каждой группе даётся задача с последующей проверкой решения у доски.
№1.2 (№125 учебника)
Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P1 и Q1. Найдите P1Q1, если PQ = 15 cм; PP1 = 21,5 cм; QQ1 = 33,5 cм.
Решение:
1) PP1 ⊥ α и QQ1 ⊥ α по условию ⇒ PP1 ∥ QQ1 (обосновать);
2) PP1 и QQ1 определяют некоторую плоскость β, α ⋂ β = P1Q1;
3) PP1Q1Q — трапеция с основаниями PP1 и QQ1, проведём PK ∥ P1Q1;
4) QK = 33,5 — 21,5 = 12 (см)
| P1Q1 = PK = | = 9 см. |
Ответ: P1Q1 = 9 см.
№2.2
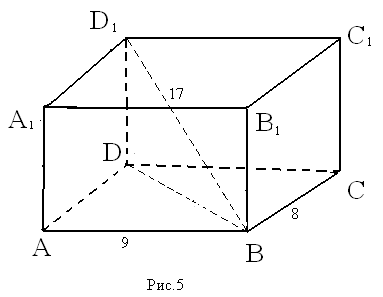
В прямоугольном параллелепипеде ABCDA1B1C1D1 АВ = 9 см; ВС = 8 см; ВD = 17 см.
Найдите площадь BDD1B1.
Решение:
1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;
| ВD = | см; |
2) ∆ DD1B: ∠D1DB = 90°;
| DD1 = | = 12 см; |
| 3) SBB1D1D = BD ∙ DD1 = | см2. |
| Ответ: | см2. |
№3.2
Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:
1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;
| 3) ∆ HPK: KP = | = 3 см; |
4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),
| тогда ∆ MEK ∆ HPK по двум углам и | ; т.е. | ⇒ EK = | = 9 см, |
РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.
Ответ: РЕ = 12 см.
3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)
| Вариант I | Вариант II | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Через вершины А и В прямоугольника АВСD проведены параллельные прямые AA1 и BB1, не лежащие в плоскости прямоугольника. Известно, что AA1 ⊥ AB, AA1 ⊥ AD. Найдите B1B, если B1D = 25 см, AB = 12 см, AD = 16 см. | Через вершины А и В ромба АВСD проведены параллельные прямые AA1 и BB1, не лежащие в плоскости ромба. Известно, что BB1 ⊥ BC, BB1 ⊥ AB. Найдите A1A, если A1C = 13 см, BD = 16 см, AB = 10 см. | ||||||||||||
|
Решение: 1) AA1 ⊥ AB, AA1 ⊥ AD, а AB ⋂ AD = A ⇒ AA1 ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA1 ∥ BB1, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD;
3) ∆ B1BD – прямоугольный. По теореме Пифагора:
Ответ: 15 см. |
Решение: 1) BB1 ⊥ AB, BB1 ⊥ BC, а AB ⋂ BC = B ⇒ BB1 ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB1 ∥ AA1, то AA1 ⊥ (ABC) ⇒ AA1 ⊥ AC;
AO = ½ AC ⇒ AC = 12 см;
Ответ: 5 см. |
Индивидуальное задание для более сильных учеников. (Вариант III)
Дано: ∆ ABC; AB = AC = BC; CD ⊥ (ABC); AM = MB; DM = 15 дм; CD = 12 дм.
Найти: S∆ ADB
Решение:
1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота;
3) DC ⊥ MC ⇒ MCD – прямоугольный,
| тогда MC = | = 9; |
4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,
| sin ∠B = | , тогда | 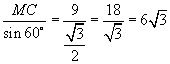 |
, |
а АВ = ВС (по условию).
5) S∆ ADB = ½ DM ∙ AB;
| S∆ ADB = ½ ∙ 15 ∙ | . |
| Ответ: |
III. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, №130, №131.
Для подготовки к уроку использовались материалы учебника «Геометрия – 10-11» авторов Л.С. Атанасяна, В.Ф. Бутузова и др., методические рекомендации к учебнику «Изучение геометрии в 10-11 классах» авторов С.М. Саакяна, В.Ф. Бутузова, «Поурочные разработки по геометрии» автора В.А. Яровенко.