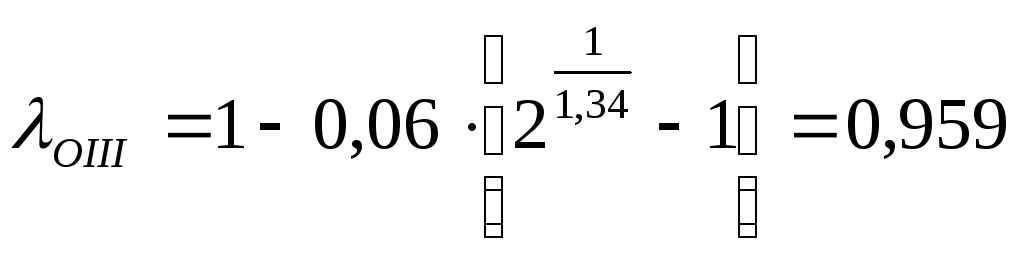Как найти площадь второго поршня

Введение

Можно ли поднять машину одним пальцем? Можно, например, воспользоваться рычагом:

Рис. 1. Перемещение машины рычагом

Правда, при этом мы совершим большее перемещение, чем перемещение груза, но зато хватит усилия, которое может создать наша рука.

Оказывается, можно сделать что-то наподобие жидкого аналога рычага. Если соединить два цилиндрических сосуда с водой и накрыть воду поршнями, то на более широкий поршень можно положить тяжелый груз, и поднять его можно будет, прикладывая небольшую силу к узкому поршню:

Рис. 2. «Водный рычаг»

Сообщающиеся сосуды

Для жидкостей выполняется закон Паскаля – давление в жидкостях передается одинаково во всех направлениях. То есть можно “надавить” в одном месте жидкости и это давление передастся во всех направлениях. Вы это используете каждый день, даже не задумываясь: надавливаете на тюбик с зубной пастой в одном месте, давление передается во всех направлениях, и паста выходит из тюбика.

Возьмем два одинаковых стакана, в стенках которых есть небольшие клапаны, чтобы можно было их соединять. Нальем в стаканы одно и то же количество воды. Масса воды одна и та же, значит, на дно стаканов будет действовать одна и та же сила. У стаканов одинаковые площади оснований, значит и давление на дно будет одно и то же. Его можно вычислить: на дно давит гидростатическое давление жидкости , вызванное силой тяжести, которая действует на воду. Стаканы открытые, поэтому на воду давит атмосфера. И по закону Паскаля жидкость передает это внешнее давление .

Соединим стаканы тонкой трубкой и откроем клапаны:

Рис. 3. Сообщающиеся сосуды

 Теперь, вода в стаканах будет сообщаться — отсюда и название сообщающиеся сосуды.

Трубку считаем очень тонкой, то есть в неё затечет так мало воды, что не повлияет на уровень воды в стаканах. Давление слева и справа от трубки одинаковое, сила давления на жидкость в трубке слева и справа одинаковая – а это и есть условие равновесия.

Здесь сравнивать давления намного удобнее, чем силы. Если давления слева и справа одинаковые, то и силы одинаковые, потому что площадь сечения трубки одна и та же.

Дольем в левый стакан воды. Давление слева увеличится, а значит, сила давления слева будет больше силы давления справа. Жидкость придет в движение и будет переливаться из левого в правый стакан.

Рис. 4. Давление жидкости в сообщающихся сосудах

Прекратится движение, когда давления снова будут равны, и жидкость установится на одном уровне.

Еще один взгляд на сообщающиеся сосуды

Почему в сообщающихся сосудах, в которые налита одна жидкость, уровень жидкости один и тот же? Это можно объяснить равенством давлений. Вода будет перетекать из одного сосуда в другой, пока давления не уравновесятся, а это произойдет при одинаковом уровне жидкости в сосудах.

Возьмем стакан. Будем его наклонять – уровень воды во всем стакане будет один и тот же. А теперь в центр стакана погрузим какое-нибудь тело. Это не помешает поверхности воды оставаться горизонтальной, это же уровень воды в одном сосуде:

Рис. 5. Уровень жидкости в стакане с погруженным телом

 И если вместо пальца погружать в воду всё более крупные тела, ничего принципиально не изменится. Нас по-прежнему не удивляет, что уровень воды в разных частях стакана будет оставаться одним и тем же, пока тело-перегородка будет оставлять просвет для перетекания воды между частями стакана (рис. 6). А это и есть сообщающиеся сосуды.

Рис. 6. Крупные тела, погруженные в воду

Что будет, если стаканы не одинаковые? Или мы их соединим по-другому? Или изменим форму сосудов и возьмем их больше двух? Или может заменим воду, на спирт, ртуть или любую другую жидкость?

Рис. 7. Пример сообщающихся сосудов

Результаты будут те же: в сообщающихся сосудах жидкость будет устанавливаться на одинаковом уровне. Ведь чтобы жидкость покоилась, нужны одинаковые давления. Атмосферное давление на все открытые сосуды одинаковое. А гидростатическое давление  будет одинаковым, если высота жидкости будет одинаковой.

Например, в строительстве часто нужно следить за горизонтальностью линий, чтобы все точки, например, стенЫ, полки или натяжного потолка, были на одном уровне. Если взять длинную гибкую трубку и налить в нее воды, то в разных концах установится один и тот же уровень воды, как бы мы ни разместили трубку:

Рис. 8. Прибор «Уровень» для строительства

На этот уровень и можно ориентироваться.

Если вода в одной части сообщающихся сосудов будет выше, чем в другой, то она начнет переливаться.

Устройство водопровода

Внутри водонапорных башен практически во всю высоту находится большой резервуар с водой. Он соединен водопроводом со всеми домами в округе (рис. 7). По сути, резервуар с водой и водопровод каждого дома – это сообщающиеся сосуды. Поскольку башня очень высокая, то уровень жидкости в резервуаре всегда выше, чем в любом из кранов. А в точке ниже уровня воды возникает гидростатическое давление :

Рис. 9. Принцип работы водонапорной башни

 Это давление и заставляет воду выливаться из крана, если его открыть. И как только вода выливается из крана, что должно привести к снижению уровня воды в водопроводе, она перетекает в дом из водонапорной башни до выравнивания уровней.

Для высотных многоэтажек система с водонапорной башней не подходит. Во-первых, проблематично построить такую высокую башню, чтобы уровень воды в ней поддерживался выше самого высокого здания. А во-вторых, даже если бы такую башню построили, в нижней части этой системы под большим столбом воды давление было бы огромным. Поэтому в высоких зданиях работает система насосов с промежуточными резервуарами на этажах, которые выполняют роль водонапорных башен.

Задача 1

Рассмотрим задачу, когда жидкости будут разные. Пусть в сообщающиеся сосуды налита вода. В правый стакан доливают небольшой столб масла высотой h. При чем так, чтобы была четкая граница раздела жидкостей и они не смешивались:

Рис. 10. Вода и масло в сообщающихся сосудах

Условие покоя жидкости всё то же: одинаковые давления в разных частях сосуда. В левом стакане давление создает атмосфера и вода:

В правом давление создает атмосфера, вода и масло:

Давления равны, значит:

Или

Атмосферное давление сократилось. Поэтому при решении подобных задач его можно не учитывать, если оба конца сосуда открыты. Если же одна часть сосуда закрыта, то на жидкость в ней не будет давить атмосфера. В таких случаях необходимо учитывать атмосферное давление в открытой части сосуда и давление газа в закрытой. Конечно, если этот газ там есть.

Ртутный барометр

Рассмотрим ситуацию, когда один из стаканов плотно накрыли крышкой. Изменится ли уровень жидкости? Нет, не изменится. В закрытом стакане по-прежнему остался воздух, который давит с атмосферным давлением. Если откачать воздух, тогда в одной части сосуда давление будет создавать жидкость и атмосфера, в другой – только жидкость:

Рис. 11. Сообщающиеся сосуды с разным атмосферным давлением

Атмосферное давление не сокращается, поэтому его необходимо обязательно учитывать.

С помощью сообщающихся сосудов с одним закрытым концом можно измерить атмосферное давление. Существуют соответствующие приборы – ртутные барометры:

Рис. 12. Ртутный барометр

 В открытой части барометра давит атмосферное давление и ртуть в “ванночке” высотой . В закрытой части сосуда давит только столбик ртути (, рисунок). Давления равны, поэтому

Измерив высоту столба ртути над уровнем “ванночки”  , можно вычислить атмосферное давление.

Обратим внимание на полученную формулу (). В левой части стоит давление воды высотой . В правой части – давление масла высотой :

Рис. 13. Уровень воды и масла в сосудах

 Видим, что полученная формула показывает равенство давлений выше некоторого уровня.

Получается, ниже данного уровня у нас только вода, находящаяся в равновесии, а над ней находятся столбец масла и столбец воды, которые оказывают одинаковые давления: для этого высота столба масла должна быть больше, у него меньше плотность.

Задача может быть сформулирована по-другому. Например, масла будет достаточно много, и оно будет находиться на дне сосудов. Или это могут быть другие жидкости. Или в сосудах будет больше двух жидкостей. В каждом из этих случаев мы всё равно сможем применить аналогичные рассуждения и так же просто всё решить:

Рис. 14. Варианты условия задачи

Каждый раз мы делаем одно и то же: записываем, что давления, создаваемые обеими частями сообщающихся сосудов, равны.

А дальше могут быть варианты. Если сосуды открыты, мы можем не рассматривать атмосферное давление, оно будет одно и то же в обеих частях сосуда. Можем выбрать уровень, ниже которого жидкость однородна: там с обеих сторон будет два столбца одной и той же жидкости одинаковой высоты, в уравнении их давления сократятся. Дальше остается рассматривать равенство давлений жидкостей выше этого уровня.

Решим задачу: в одно колено сообщающихся сосудов с водой долили масло, высота столба масла . Найти разность установившихся уровней жидкости.

Решение задачи

В задаче описаны сообщающиеся сосуды. Жидкость находится в равновесии, запишем равенство давлений:

Рис. 15. Уровень однородной жидкости

Слева давление оказывает столбик воды под пунктиром (), столбик воды над пунктиром () и атмосферное давление . Справа давление оказывает столбик воды под пунктиром (), столбик масла  и атмосферное давление . Запишем:

Из таблицы плотностей: , .

Выразим :

То есть уровень воды будет ниже уровня масла на . Задача решена.

Гидравлический пресс

Мы рассмотрели случай, когда жидкость передаёт гидростатическое и атмосферное давление. Эти давления возникают из-за притяжения к Земле, мы на них не влияем. Но ведь мы можем сами “надавить” на жидкость, и она передаст это давление.

Если надавить на жидкость в одной части сосуда, давление передастся в другую. Устройство, работающее на таком принципе, называется гидравлическим прессом:

Рис. 16. Гидравлический пресс

Внешнее давление создается поршнем, на который действуют с некоторой силой . Поршень действует с такой же силой  на жидкость и создаёт давление , где  – площадь поршня.

Жидкость находится на одном уровне, поэтому гидростатическое давление можем не учитывать: они и так будет одинаковое в обеих частях гидравлического пресса. Значит, на второй поршень передастся такое же давление . Можно вычислить силу, которая будет действовать на второй поршень площадью :

Прикладывая меньшую силу, хочется получить большую. Для этого площадь второго поршня должна быть больше площади первого. Во сколько раз она будет больше, во столько раз будет больше и сила.

Преобразуем полученное выражение для гидравлического пресса:

Полученное выражение более наглядно показывает принцип действия гидравлического пресса: давления на поршни  одинаковы: .

Почему именно жидкость применяется в гидравлическом прессе

Можно ли придумать похожее устройство, но без жидкости? Твердое тело использовать не получится – для него не выполняется закон Паскаля, а на нем основан принцип действия пресса. Но закон Паскаля выполняется не только для жидкостей, но и для газов. Существуют приборы, использующие газ. Они называются пневматическими прессами и тоже используются, как и гидравлические.

Молекулы в жидкости расположены близко, её можно считать несжимаемой. А вот в газе молекулы расположены на расстояниях бОльших, чем размеры самих молекул, газ можно сжать. При изменении объема, меняется и давление, которое он создает. Поэтому механизм работы пневматического пресса описать сложнее. Так что остановимся только на гидравлическом прессе.

Задача 2

С помощью гидравлического пресса необходимо приподнять машину массой 1,5 тонны лишь одним пальцем:

Рис. 17. Гидравлический пресс и машина

 Считать, что площадь одного поршня совпадает с площадью подушечки пальца (20 мм²). Необходимо найти площадь второго поршня, на котором будет стоять машина. Будем считать, что палец может давить с силой 1,5 Н.

Запишем формулу для гидравлического пресса:

Одна сила – это действие пальца, по условию . А сила, которая действует на второй поршень – это вес автомобиля . Запишем: . Осталось выразить  и, подставив численные значения, получить площадь второго поршня 0,2 м².

Решение задачи

Вычислим силу :

В формуле гидравлического пресса  перемножим по правилу пропорции:

Выразим :

Чтобы приподнять машину хотя бы на 1 мм, нужно сдвинуть поршни. При этом жидкость перельется из одной части пресса в другую. Посчитаем, на сколько же опустится меньший поршень. Чтобы под больший поршень перелился некоторый объем жидкости, он должен вытечь из-под меньшего поршня. Для поднятия большего поршня на 1 мм туда должен перетечь объем: . Из-под меньшего поршня вытечет тот же объем . Тогда поршень опустится на . Видим, что, получив большой выигрыш в силе, мы вынуждены переместить поршень на большое расстояние. Именно поэтому неограниченно увеличивать силу мы не сможем – тогда придётся очень далеко перемещать поршень.

Теперь нужно учитывать дополнительное гидростатическое давление: мы поднимаем не только груз, но еще и столб жидкости выше малого поршня:

Рис. 17. Гидравлический пресс и машина

Учесть дополнительное давление можно: просто записываем равенство давлений в разных частях сообщающихся сосудов.

Как избежать разности гидростатических давлений

Мы рассмотрели стандартный вид гидравлического пресса. Но можно его немного изменить:

Рис. 15. Гидравлический пресс другого вида

Принцип работы не поменяется, жидкость по-прежнему будет передавать внешнее давление. Зато высота жидкости возле меньшего поршня изменяться не будет, он будет находиться на одном уровне, и мы сможем использовать формулу для гидравлического пресса. Но всё равно придется перемещать меньший поршень на 10 метров, что очень неудобно.

В реальных же гидравлических прессах перемещения поршней достаточно малы, чтобы изменением высоты жидкости можно было пренебречь. И тогда можно использовать формулу:

Домашнее задание

1. Расскажите о принципе работы фонтанов
2. Малый поршень гидравлического пресса за один ход опускается на расстояние , а большой поршень поднимается на высоту . С какой силой  действует пресс на зажатое в нем тело, если на малый поршень действует сила ?
3. В левое колено u-образной трубки с водой долили слой керосина высотой . На сколько поднимется уровень воды в правом колене?

Список рекомендованной литературы

1. Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
2. Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
3. Генденштейн Л. Э., Кирик Л. А. Решение ключевых задач по физике для основной школы. 7-9 классы. – М., 2013, — 208с.

Рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «solverbook.com» (Источник)
2. Интернет-портал «files.school-collection.edu.ru» (Источник)

Гидравлический пресс даёт выигрыш в силе в 100 раз. Найдите площадь большего поршня и его силу, если на меньший поршень

Ответ или решение 2

Чтобы понять, как работают гидравлические машины, нужно понимать:

1. теорию сообщающихся сосудов;
2. определение давления через силу давления и площадь, на которую оказывается давление;
3. принципиальное устройство гидравлических машин.

Анализ условия задачи

Пусть дан гидравлический пресс. Из условия задачи известно, что он даёт выигрыш в силе в 100 раз, то есть сила давления, оказываемая на больший поршень превышает силу давления, оказываемую на меньший поршень в сто раз: F₁ : F₂ = 100. Чтобы найдите площадь большего поршня S₁ и силу, действующую с его стороны F₁ на внешние тела, если на меньший поршень, площадью S₂ = 1 см² = 0,0001 м² действует сила F₂ = 100 Н, воспользуемся законом Паскаля, по которому давление, создаваемое в какой-то точке жидкости, передаётся по всем направлениям одинаково. Значит, давление на оба поршня будет одинаковым: р₁ = р₂. По определению давление р равно отношению силы давления к площади, на которую это давление оказывается, то есть: р = F : S. Для первого и второго поршня получаем: р₁ = F₁ : S₁ и р₂ = F₂ : S₂. Тогда получается, что: F₁ : S₁ = F₂ : S₂.

Расчёт площади поршня и силы давления

Так как F₁ : F₂ = 100, то F₁ = 100 ∙ F₂ и (100 ∙ F₂) : S₁ = F₂ : S₂, или S₁ = 100 ∙ S₂. Подставим значения физических величин в расчётные формулы и найдём площадь большего поршня:

и силу давления, создаваемую им:

Ответ: площадь большего поршня составляет 0,01 м²; а сила давления, создаваемая им равна 10 кН.

Давление равно силе деленной на площадь P = F/S.

Давление на малый поршень PМ:

Давление создаваемое большим поршнем:

Давление под большим поршнем и под малым поршнем одно и то же:

Источник статьи: http://vashurok.ru/questions/gidravlicheskiy-press-dayot-viigrish-v-sile-v-100-raz-naydite-ploschad-bolshego-porshnya

Гидростатика. Гидравлический пресс.

Гидравлический пресс — это пример элементарной гидравлической машины, применяемой для формирования значительных сжимающих усилий. Ранее его принято было называть «пресс Брама», в честь изобретателя Джозефа Брама. Он запатентовал свое изобретение в 1795 году.

Гидравлический пресс предоставляет возможность получить значительный выигрыш в силе, при минимальных затратах.

Цилиндры несхожих диаметров, плотно закрытые сверху поршнями, образуют основу всякого гидравлического пресса. Причем эти цилиндры должны быть сообщающимися сосудами.

Цилиндры наполнены жидкостью (к примеру, водой, но в большинстве случаев маслом, либо иной жидкостью).

Схематически гидравлический пресс имеет вид:

Площадь левого поршня S₁ во много раз меньше площади правого поршня S₂.

Силы, воздействующие на поршни, соразмерны площадям этих поршней. Так когда, к левому поршню приложена сила F₁, эта сила будет действовать на жидкость, распределяясь по площади S₁. Давление, оказываемое левым поршнем на жидкость, получиться найти по формуле:

Согласно закону Паскаля это давление будет величиной постоянной во всяком месте жидкости. Из этого можно сделать вывод, что давление, оказываемое на правый поршень, примем его равным, p₂, будет тоже:

Свяжем это давление с силой, которая воздействует со стороны жидкости на правый поршень:

Следовательно, сила, воздействующая на большой поршень, будет во столько раз больше силы, приложенной к малому поршню, во сколько раз площадь большого поршня больше площади малого поршня.

Перефразировав имеем, гидравлическая машина предоставляет возможность получить выигрыш в силе, определяемый соотношением площади большего поршня к площади меньшего поршня.

Гидравлическими тормозами оборудованы автомобили, мотоциклы и современные велосипеды. Автолюбители повсеместно пользуются гидравлический домкрат. Гидравлический привод нашел применение на бульдозерах, погрузчиках, кранах. Современные гидравлические прессы формируют усилие в несколько миллионов ньютонов.

Источник статьи: http://www.calc.ru/Gidrostatika-Gidravlicheskiy-Press.html

1. Определение активной площади поршней

Активная
площадь поршня ступени с номером i,
находится по формуле

,
(19)

где

– секундный объём, описываемый поршнем
этой ступени, м³/с;

– средняя скорость поршня, м/с. Принимая

м/с, получим

м²,

м².

1. Определение предварительных значений диаметров цилиндров

В ступенях
двойного действия со штоком с одной
стороны поршня, диаметры цилиндра
находятся по формуле

,
(20)

где

– площадь штока, принимаемая равной

(21)

Отсюда можно
выразить

(22)

м.

м².

м.

Полученные
диаметры цилиндров необходимо округлить
до номинальных диаметров поршневых
колец (см. [1], стр. 355, табл. П.1). Тогда
диаметры цилиндров принимаем равные:
м
и
м,
следовательно диаметры поршней равны:
м
и
м.

1. Определение частоты вращения коленчатого вала компрессора

Частота
вращения коленчатого вала n,
об/мин, определяется по формуле:

,
(23)

где S
– ход поршня, выбираем

м, то есть ход поршня из стандартного
ряда, тогда

об/мин.

1. Определение индикаторной мощности компрессора

Индикаторная
мощность компрессора

определяется по формуле:

,
(24)

где z
– число ступеней;

– индикаторная мощность i-й
ступени, которая определяется из
уравнения

,
(25)

где Р_ВСi
– давление на всасывании в ступень;

– средняя относительная потеря давления
на всасывании в ступень;

– секундная теоретическая производительность
ступени; а_i
– относительная величина мёртвого
пространства ступени;

– отношение давлений в цилиндре.

Определим
все величины, входящие в выражение для
индикаторной мощности ступеней. Согласно
[1], п. 2.5 средние относительные потери
давления во всасывающих и нагнетательных
клапанах находятся по формуле (11), тогда
имеем:

,

.

Учитывая, что
после первой ступени компрессора имеется
холодильник, относительная потеря на
нагнетании I-й ступени с
учётом потерь давления в межступенчатой
коммуникации

(26)

.

Отношение
давлений газа в цилиндрах:

,
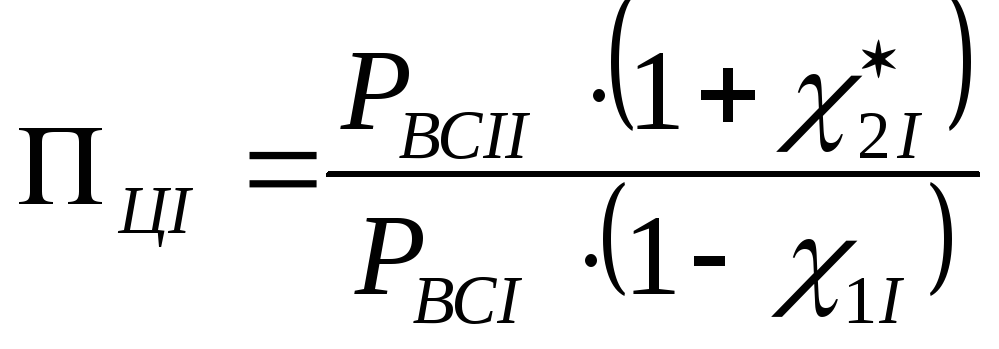
(27)

;
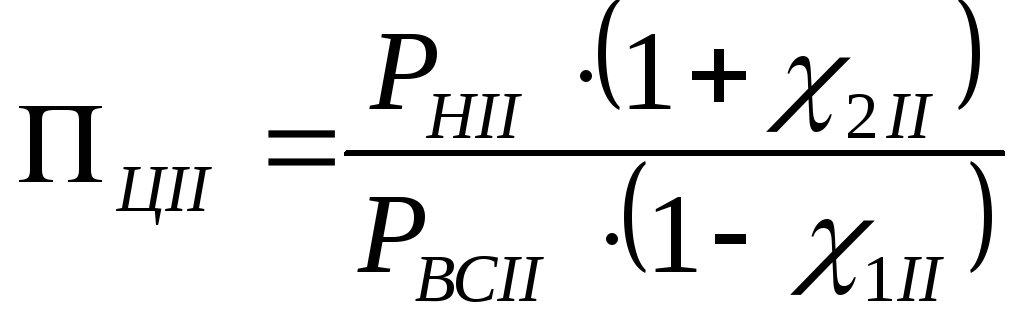
(28)

,

.

Значения
величин А_Сi
и A_Pi
определяем по формулам:

,
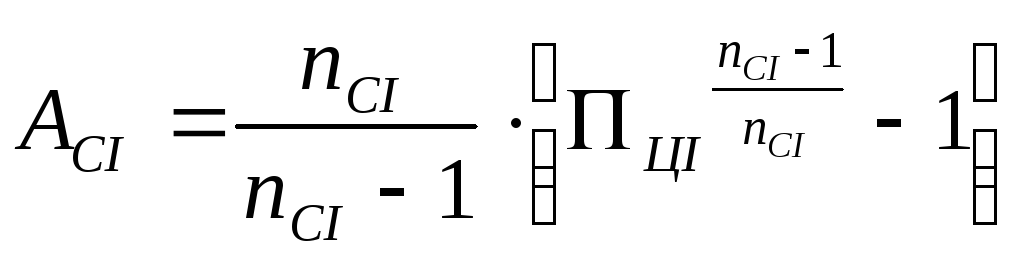
(29)

;
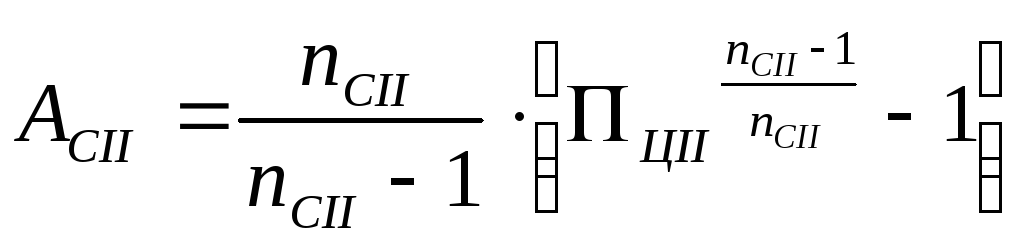
(30)

,

;

,
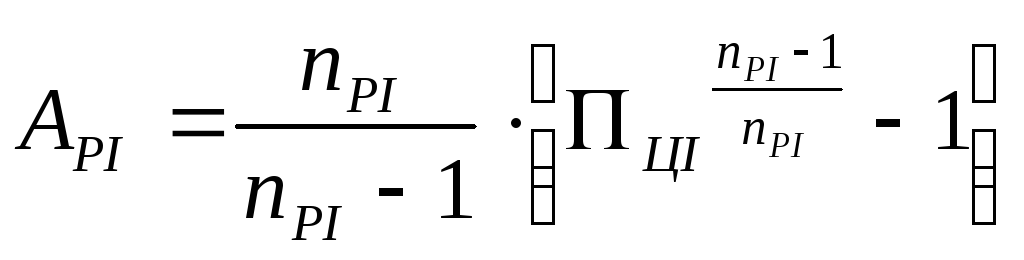
(31)

;
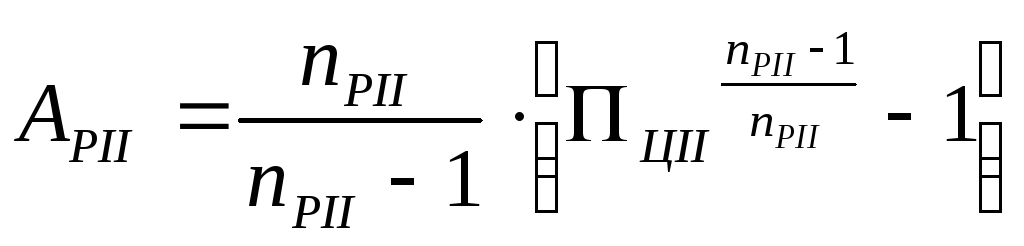
(32)

,

;

Подставим
всё известные величины в формулы для
определения индикаторной мощности
ступеней:

Вт,

Вт.

Индикаторная
мощность компрессора определяется по
формуле (24):

кВт.

1. Определение мощности, потребляемой
   компрессором

Мощность,
потребляемая компрессором, определяется
из уравнения:

,
(33)

где

– механический коэффициент полезного
действия компрессора, которым задаются,
используя статистические данные близких
по параметрам машин. Принимая
:

кВт.

1. Определение полезного действия
   компрессора

Совершенство
многоступенчатых компрессоров оценивается
изотермным коэффициентом полезного
действия:

,
(34)

где N_ИЗ
– изотермная мощность компрессора,
вычисляемая по формуле:

,
(35)

кВт,

тогда

.

1. Термодинамический расчёт трёхступенчатого
   компрессора

   1. Определение необходимого числа
      ступеней сжатия в компрессоре

Общее
отношение давлений в компрессоре найдём
по аналогии формулы (1):

.

На основании
статистических данных по уже выполненным
компрессорам (см. [1], стр. 92, рис. 3.5) выберем
число ступеней равное трём.

.

1. Распределение давлений по ступеням
   сжатия

По формуле
(3):

.

1. Определение секундных объёмов,
   описываемых поршнями первой и второй
   ступени

Для II-й
ступени по формуле (4), для I-й
ступени по формуле (5), III-я
ступени находится аналогично второй.

Определим
составляющие коэффициента производительности
для каждой ступени.

По заданию,
значения относительного мёртвого
пространства
,
,
.

По формуле
(9):

.

Теперь, найдём

и

по формуле (8):

.

Принимая по
формуле (7)
,
получим:

,

,

.

По формуле
(6) находим величину
:

,

,

Выберем

,

тогда по
формуле (11):

,

.

Вычислим
значения

по формуле (10):

,

,

.

Вычислим
значения

по формуле (12), принимая
,
,
:

,

,

.

Принимаем

.

По формуле
(13):

.

Теперь,
имея все составляющие коэффициента
производительности, определяем значения
самих коэффициентов:

,

,

.

Плотность
воздуха
,
определяем по формуле (14):

кг/м³.

По формуле
(16):

Па,

Па.

По формуле
(17):

К.

К.

Тогда по
формуле (15):

кг/м³.

кг/м³.

По формуле
(18):

кг/с.

Теперь, имея
всё необходимые составляющие для
определения объёмов, описываемых
поршнями, найдём эти объёмы

м³/с,

м³/с.

м³/с.

1. Определение активной площади поршней

По формуле
(19), принимая

м/с, получим:

м²,

м²,

м².

1. Определение предварительных значений
   диаметров цилиндров

По формуле
(22):

м.

Тогда по
формуле (21):

м².

По формуле
(20):

м.

м.

1. Определение частоты вращения коленчатого
   вала компрессора

По формуле
(23), выбирая

м:

об/мин.

1. Определение индикаторной мощности
   компрессора

Определим
все величины, входящие в выражение для
индикаторной мощности ступеней.

По формуле
(11):

,

,

.

По формуле
(26):

По формулам
(27) и (28):

,

,

.

По формулам
(29) и (30):

,

,

;

,

,

.

Тогда, зная
все составляющие, имеем по формуле (25):

кВт,

кВт,

кВт.

По формуле
(24):

кВт.

1. Определение мощности, потребляемой
   компрессором

Принимая
,
по формуле (33):

кВт.

1. Определение полезного действия
   компрессора

По формуле
(35):

кВт,

Тогда по
формуле (34):

.

1. Выбор оптимального количества
   ступеней в компрессоре

Проанализировав
термодинамические расчеты для двух- и
трёхступенчатого компрессов, можно
сделать следующий вывод.

С увеличением
количества ступеней, уменьшаются
диаметры цилиндров, а следовательно и
габариты компрессора. Уменьшается
отношение давлений для ступеней, что
влечёт уменьшение затрачиваемой мощности
и повышение коэффициента полезного
действия компрессора. Также уменьшается
газовая сила, действующая на поршень,
что благоприятно влияет на надёжность
и уменьшает металлоёмкость конструкции.

Но, в нашем
случае, увеличение количества ступеней,
связанно с увеличением количества рядов
компрессора. Это увеличивает металлоёмкость
компрессора и занимаемую им площадь.
Также, это усложняет конструкцию
межступенчатых коммуникаций и самого
компрессора.

Для
дальнейшего расчёта, выбираем
двухступенчатую схему компрессора.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вопрос по физике:

Помогите ,пожалуйста, завтра контрольная, а я не знаю!!!
1) Как найти площадь поршня гидравлического пресса, если известна сила, которая давит на него, площадь второго поршня и сила, которая давит на второй поршень.
2) Как найти силу, которая давит на первый поршень, если известна площадь этого поршня, площадь второго поршня и сила, давящая на второй поршень.
(Если возникнут вопросы, то задавайте) Ответ запишите формулами и словами.
PLEASE, очень надо!!!