Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
33 473
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.
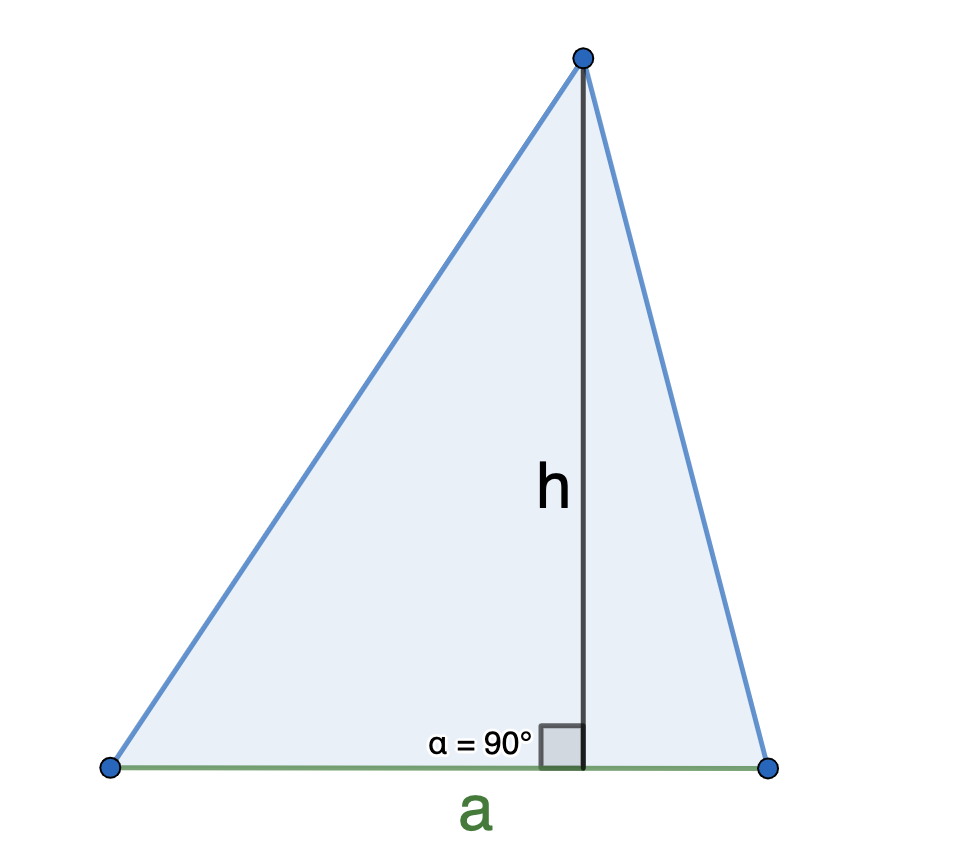
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
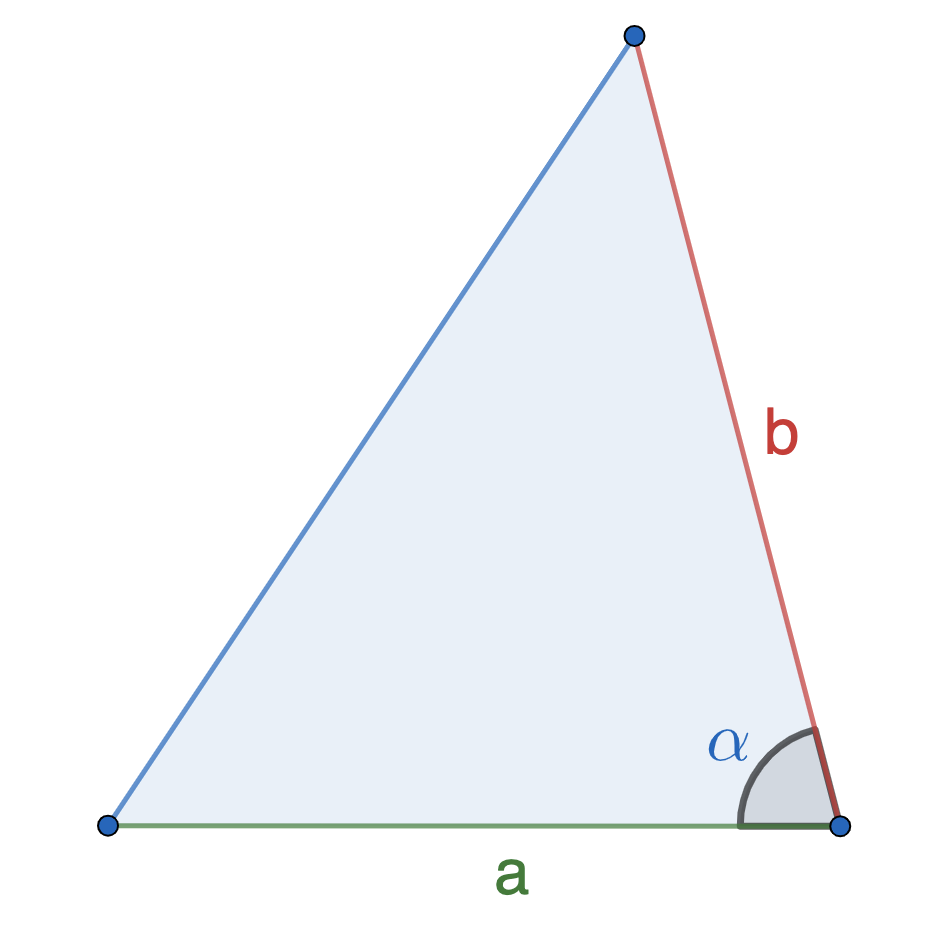
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Делайте так:
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
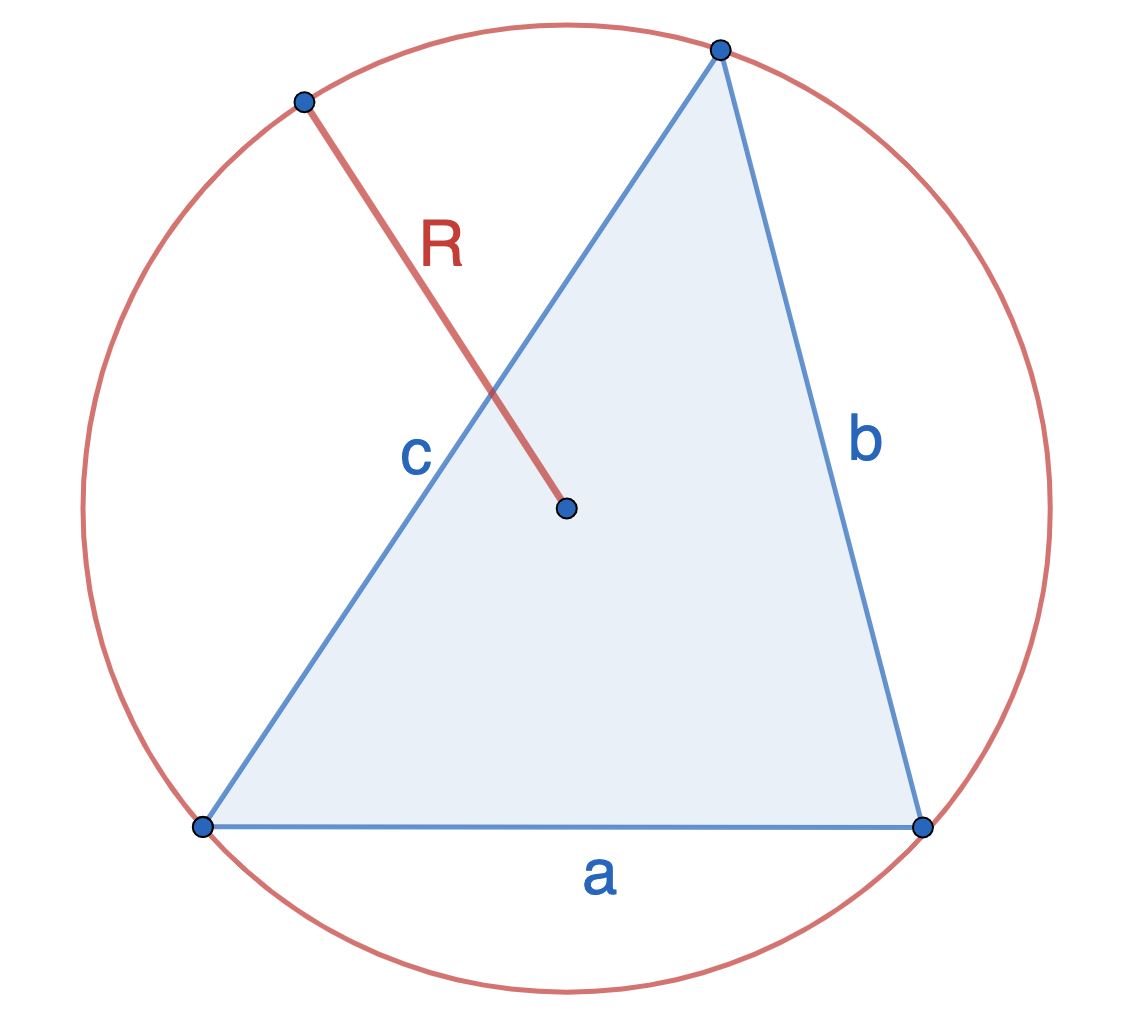
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
( 32 оценки, среднее 4.44 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ
{S=sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Эти три точки называют вершинами треугольника, а отрезки — сторонами треугольника.
На рисунке мы видим три вершины, которые обозначены буквами A, B и C.
Также на рисунке изображены 3 стороны треугольника. Их можно обозначать по вершинам, которые их ограничивают. Например, сторона AB, сторона BC и сторона AC. Но для удобства вершины можно обозначать короче. В примере на рисунке сторону AB можно обозначить как b, BC как c, а AC как a.
Формула для вычисления площади треугольника по 3 сторонам
Для нахождения площади треугольника по трем сторонам используют формулу Герона.
{S=sqrt{p(p-a)(p-b)(p-c)}}
{p=dfrac{a+b+c}{2}}
a, b, c — длины сторон треугольника,
p — полупериметр треугольника.
Примеры решения задач по нахождению площади треугольника
Задача 1
Найти площадь треугольника со сторонами 6 6 8.
Решение
Перед тем, как искать площадь треугольника по трем сторонам, необходимо найти его полупериметр. Для этого сложим длины его сторон и разделим сумму на 2:
p = dfrac{a+b+c}{2} = dfrac{6+6+8}{2} = dfrac{20}{2} = 10
Теперь, зная полупериметр, можем воспользоваться формулой Герона и найти площадь треугольника:
S=sqrt{p(p-a)(p-b)(p-c)}=sqrt{10(10-6)(10-6)(10-8)}=sqrt{10 cdot 4 cdot 4 cdot 2} = sqrt{320} approx 17.88854
Ответ: sqrt{320} approx 17.88854
Осталось проверить ответ с помощью калькулятора .
Задача 2
Найти площадь треугольника со сторонами 5 7 6.
Решение
Как и в задаче выше начнем решение с нахождения полупериметра треугольника:
p = dfrac{a+b+c}{2} = dfrac{5+7+6}{2} = dfrac{18}{2} = 9
Далее подставим значения в формулой площади треугольника и найти ее:
S=sqrt{p(p-a)(p-b)(p-c)}=sqrt{9(9-5)(9-7)(9-6)}=sqrt{9 cdot 4 cdot 2 cdot 3} = sqrt{216} approx 14.69694
Ответ: sqrt{216} approx 14.69694
Осталось проверить ответ с помощью калькулятора .
Формула Герона применяется в различных областях, где необходимо находить площадь треугольника, в том числе:
- В геометрии для вычисления площади треугольников, например, при решении задач на нахождение площади или при вычислении высоты треугольника.
- В архитектуре и строительстве для расчета площади треугольных конструкций, например, крыш, заборов, деревянных конструкций и т.д.
- В физике для определения площади поверхности треугольных объектов, например, площади основания при вычислении объема пирамиды.
- В тригонометрии для решения задач, связанных с треугольниками.
- В механике для вычисления площади треугольной области, ограниченной маятником при расчете периода колебаний.
В целом, формула Герона широко используется в различных областях, где требуется находить площадь треугольника через три стороны, и является одной из наиболее распространенных формул геометрии.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Найти площадь треугольника можно различными способами. Конечно же, в зависимости от данных переменных и подбирается необходимая формула. В основном, для нахождения площади треугольника применяется формула Герона.
Если известны все три стороны треугольника ABC, то формула площади треугольника по трем сторонам легко применится на практике:
где:
- p – полупериметр треугольника,
- a, b, c – длины сторон треугольника.
Периметр – это сумма длин всех сторон треугольника. Соответственно полупериметр – это сумма длин всех сторон разделенная на 2.
Рассмотрим пример расчета площади треугольника по трем сторонам:
Дан треугольник. Стороны a = 3 см., b = 4 см., c = 5 см. Для начала найдем полупериметр
=6 см.
Далее рассчитаем площадь
Площадь треугольника равна 6 кв. см
Также можно найти площадь треугольника и по другим формулам – через синус и косинус.
| Сторона a= | Сторона b= | Сторона c= | |
| Ответ: Площадь треугольника = 6.000 |
Формула площади треугольника по основанию и высоте
(S = {{a*h} over 2})
(a) — сторона к которой проведена высота (основание)
(h) — высота
Формула площади треугольника через две стороны и угол между ними
(S = 0,5*a*b*sinalpha)
a, b — стороны, прилежащие к углу (alpha)
Формула площади треугольника через три стороны и описанную окружность
(S = frac{a*b*c}{4R})
(R) — радиус описанной окружности
(a, b, c) — длины сторон треугольника
Примеры
1. Найдите площадь треугольника, если две его стороны равны 6 см и 12 см, а угол между этими сторонами равен 30 градусов.
Решение:
(S= 0,5 *a*b*sin alpha= 0,5*6*12*sin30 = 18) (Ответ 18 см2)
2. Найдите площадь треугольника, если высота равна 4 см. , а основание равно 8 см.
Решение:
(S = {{a*h} over 2} = {{8*4} over 2} = 16) (Ответ 16 см2)
3. Треугольник вписан в окружность радиусом 10см. Длины сторон треугольника 8 см, 6 см и 4 см. Найдите площадь вписанного треугольника со сторонами, равными этим числам, зная радиус описанной окружности.
Решение:
(S = frac{a*b*c}{4R} = frac{8*6*4}{4*10} = 4,8)