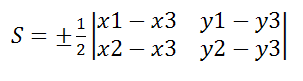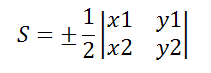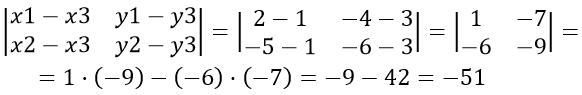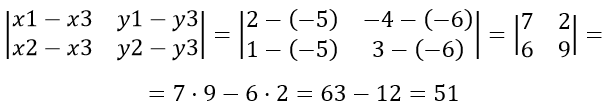Площадь треугольника по координатам вершин — формулы для расчета
Самый простой многоугольник и вектор
Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.
Фигура на плоскости
Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.
Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.
Для треугольника важное значение имеют следующие отрезки:
- делящий противоположную углу сторону пополам — медиана;
- разделяющий угол при вершине на два равных — биссектриса;
- падающий под прямым углом на противоположную углу сторону — высота.
Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.
Направленный отрезок
Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.
Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:
AB- = B-A = (x1-x0; y1-y0).
Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.
Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:
- Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
- Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.
Методы вычисления площади по координатам
Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.
Универсальный подход
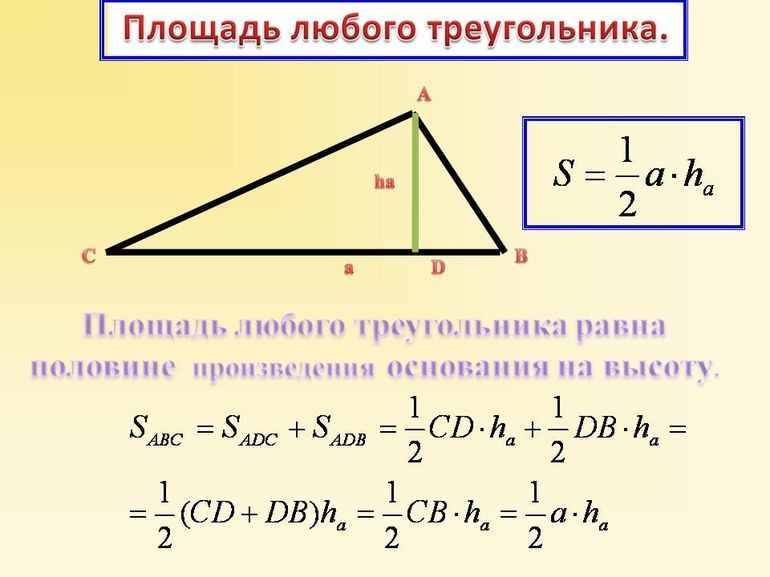
Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.
Пусть имеются координаты вершин заданного треугольника ABC:
Тогда координаты его векторов AB- и AC- выразятся так:
Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:
Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).
Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:
S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).
Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.
Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.
Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.
Использование формулы Герона
Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:
Здесь p — полупериметр, a, b, c — длины сторон.
Последовательность этапов решения задачи можно выразить таким образом:
- Необходимо определить координаты векторов, образующих стороны треугольника.
- Затем, следует вычислить длины их сторон.
- Посчитать полупериметр фигуры.
- Применить формулу Герона.
Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:
|AB-| = (x1 2 + y1 2 )^0,5.
Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.
Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.
Другие способы
Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:
- Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
- Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).
Решение задачи
Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).
Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:
Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.
Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.
Онлайн калькулятор. Площадь треугольника построенного на векторах.
Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденый материал.
Калькулятор для вычисления площади треугольника построенного на векторах
Выберите каким образом задается треугольник:
Введите значения векторов: Введите координаты точек:
Инструкция использования калькулятора для вычисления площади треугольника построенного на векторах
Ввод данных в калькулятор для вычисления площади треугольника построенного на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Площадь треугольника построенного на векторах
Определение Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Площадь треугольника, построенного на векторах: онлайн-калькулятор
Формула площади треугольника заложена в программе и вычисляет половину модуля векторного произведения:
Чтобы найти площадь треугольника, необходимы задать значения двух векторов или координаты вершин треугольника. После этого вы получите готовое решение с пояснениями и ответ. Сервис используют школьники, их родители, студенты, преподаватели.
- Выберите форму представления треугольника «Двумя векторами сторон».
- Введите значения векторов a и b в соответствующие поля. Отправьте задание на решение кнопкой «Рассчитать»
- Получите решение и ответ.
- Выберите форму представления треугольника «Координатами точек».
- Введите координаты вершин A, B, C в соответствующие поля. Отправьте задание на решение кнопкой «Рассчитать».
- Получите решение и ответ.
Материалы, которые помогут вам лучше разобраться в теме:
Как найти площадь треугольника, построенного на векторах
Онлайн-калькулятор позволяет учащимся готовиться к занятиям, разбираться в непонятной теме, тренироваться на примерах. Расчеты производятся бесплатно, поэтому вы сможете сэкономить деньги на репетиторе и самостоятельно осваивать материал. Моментальное решение также поможет сдать зачет или экзамен, написать контрольную на хорошую оценку. Родители смогут быстро проверить домашнее задание ребенка, а преподаватели – автоматизировать процесс создания обучающих материалов.
Чтобы вычислить площадь треугольника через векторы, программа выполняет следующие действия:
- Анализирует введенные данные. Если указаны координаты точек, рассчитываются векторы a и b.
- Находит произведение векторов.
- Вычисляет модуль вектора.
- Делит результат на 2 и выдает ответ.
С помощью нашего сайта вы сможете изучить, как найти площадь треугольника не только по векторам, но и другими способами. Мы разделили калькуляторы по темам для удобного использования. Так вы быстро найдете нужную тему и получите правильный ответ. В автоматических расчетах исключена потеря данных между действиями, опечатки. Благодаря калькулятору вы сможете сравнить решение с собственным и найти ошибку.
http://ru.onlinemschool.com/math/assistance/vector/triangle_area/
http://zaochnik.com/online-calculators/operacii-nad-vektorami/ploshad-treugolnika-postroennogo-na-vektorah/
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Содержание
§
Вспомогательная страница к разделу
☞
ОПРЕДЕЛИТЕЛЬ
Геометрические приложения определителя
Уравнения кривых и поверхностей
Уравнение прямой, проходящей через точки плоскости с координатами $ (x_{1},y_1) $ и $ (x_{2},y_2) $:
$$
left|
begin{array}{lll}
x & y & 1 \
x_1 & y_1 & 1 \
x_2 & y_2 & 1
end{array}
right|=0 qquad iff qquad
left|
begin{array}{ll}
x-x_1 & y-y_1 \
x_2-x_1 & y_2-y_1
end{array}
right|=0 .
$$
Уравнение окружности, проходящей через точки плоскости с координатами $ (x_{1},y_1) , (x_2,y_2) $ и $ (x_{3},y_3) $ (окружности, описанной вокруг треугольника):
$$
left|
begin{array}{llll}
x^2+y^2 & x & y & 1 \
x_1^2+y_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2 & x_2 & y_2& 1 \
x_3^2+y_3^2 & x_3 & y_3& 1
end{array}
right|=0 .
$$
При условии, что все три точки коллинеарны (лежат на одной прямой; см.
☞
ЗДЕСЬ ):
$$
left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|=0
$$
окружность вырождается в прямую
$$
left|
begin{array}{clll}
0 & x & y & 1 \
x_1^2+y_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2 & x_2 & y_2& 1 \
x_3^2+y_3^2 & x_3 & y_3& 1
end{array}
right|=0 .
$$
Координаты центра окружности, проходящей через точки $ (x_{1},y_1) , (x_2,y_2) $ и $ (x_{3},y_3) $:
$$
x_C=frac{left|
begin{array}{lll}
x_1^2+y_1^2 & y_1 & 1 \
x_2^2+y_2^2 & y_2& 1 \
x_3^2+y_3^2 & y_3& 1
end{array}
right|}
{2left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|},quad
y_C=-frac{left|
begin{array}{lll}
x_1^2+y_1^2 & x_1 & 1 \
x_2^2+y_2^2 & x_2& 1 \
x_3^2+y_3^2 & x_3& 1
end{array}
right|}
{2left|
begin{array}{lll}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1
end{array}
right|} .
$$
Т
Теорема [Птолемей]. Точки
$$ P_1=(x_{1},y_1) , P_2=(x_2,y_2), P_3 =(x_{3},y_3), P_4=(x_{4},y_4) $$
лежат на одной окружности или на одной прямой тогда и только тогда, когда выполнено равенство
$$
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0
end{array}
right|=0 .
$$
Здесь $ |P_jP_k|^2=(x_j-x_k)^2+(y_j-y_k)^2 $.
Доказательство, альтернативная геометрическая формулировка, а также пространственный аналог теоремы
☞
ЗДЕСЬ.
Уравнение плоскости, проходящей через точки пространства с координатами $ (x_{1},y_1,z_1) $, $ (x_{2},y_2,z_2) $ и $ (x_{3},y_3,z_3) $:
$$
left|
begin{array}{llll}
x & y & z & 1 \
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1
end{array}
right|=0 .
$$
Уравнение сферы, проходящей через точки $ (x_{1},y_1,z_1) $, $ (x_{2},y_2,z_2) $, $ (x_{3},y_3,z_3) $ и $ (x_{4},y_4,z_4) $:
$$
left|
begin{array}{cllll}
x^2+y^2+z^2 & x & y & z & 1 \
x_1^2+y_1^2+z_1^2 & x_1 & y_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & y_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & y_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & y_4 & z_4 & 1
end{array}
right|=0 .
$$
При условии, что все четыре точки компланарны (лежат в одной плоскости; см.
☞
ЗДЕСЬ ):
$$
left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|=0
$$
сфера вырождается в плоскость. Координаты центра сферы:
$$
x_C=frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & y_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & y_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & y_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & y_4 & z_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|},
y_C=-frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & x_1 & z_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & z_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & z_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & z_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|},
z_C=frac{left|
begin{array}{clll}
x_1^2+y_1^2+z_1^2 & x_1 & y_1 & 1 \
x_2^2+y_2^2+z_2^2 & x_2 & y_2 & 1 \
x_3^2+y_3^2+z_3^2 & x_3 & y_3 & 1 \
x_4^2+y_4^2+z_4^2 & x_4 & y_4 & 1
end{array}
right|}{2,left|
begin{array}{llll}
x_1 & y_1 & z_1 & 1 \
x_2 & y_2 & z_2 & 1 \
x_3 & y_3 & z_3 & 1 \
x_4 & y_4 & z_4 & 1
end{array}
right|}
$$
§
Сформулированные выше геометрические задачи являются частными случаями общей задачи об
☞
ИНТЕРПОЛЯЦИИ.
Площади
Площадь треугольника с вершинами $ P_1=(x_{1},y_1) , P_2=(x_{2},y_2) $ и $ P_3=(x_{3},y_3) $ равна абсолютной величине (модулю) выражения
$$
frac{1}{2}
left|
begin{array}{lll}
1 & x_1 & y_1 \
1 & x_2 & y_2 \
1 & x_3 & y_3
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Квадрат площади треугольника $ P_{1}P_2P_3 $ выражается через квадраты длин его сторон по формуле
$$
S^2=-frac{1}{16}
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| ,
$$
которая в развернутом виде
$$
=frac{1}{16}left(|P_1P_2|+|P_1P_3|+|P_2P_3| right)left(|P_1P_2|+|P_1P_3|-|P_2P_3| right)left(|P_1P_2|-|P_1P_3|+|P_2P_3| right)
left(-|P_1P_2|+|P_1P_3|+|P_2P_3| right)
$$
представляет собой формулу Герона.
Площадь треугольника с вершинами $ P_1=(x_{1},y_1,z_1) , P_2=(x_{2},y_2,z_2) $ и $ P_3=(x_{3},y_3,z_3) $ в $ mathbb R^{3} $ равна
$$
frac{1}{2} sqrt{ left|
begin{array}{lll}
1 & x_1 & y_1 \
1 & x_2 & y_2 \
1 & x_3 & y_3
end{array}
right|^2
+
left|
begin{array}{lll}
1 & x_1 & z_1 \
1 & x_2 & z_2 \
1 & x_3 & z_3
end{array}
right|^2+
left|
begin{array}{lll}
1 & y_1 & z_1 \
1 & y_2 & z_2 \
1 & y_3 & z_3
end{array}
right|^2
} .
$$
Выражение под радикалом можно преобразовать к виду
$$
detleft[left(
begin{array}{lll}
x_2-x_1 & y_2-y_1 &z_2- z_1 \
x_3-x_1 & y_3-y_1 & z_3- z_1
end{array}
right)cdot left(
begin{array}{ll}
x_2-x_1 & x_3-x_1 \
y_2-y_1 & y_3-y_1 \
z_2-z_1 & z_3-z_1
end{array}
right)right]
$$
с помощью теоремы Бине-Коши. Таким образом, площадь треугольника также равна
$$
frac{1}{2} sqrt{ left|
begin{array}{cc}
langle P_2P_1,P_2P_1 rangle & langle P_2P_1,P_3P_1 rangle \
langle P_2P_1,P_3P_1 rangle & langle P_3P_1,P_3P_1 rangle
end{array}
right|} ,
$$
где скобками $ langle , rangle $ обозначено скалярное произведение.
Площадь четырехугольника с вершинами $ P_1=(x_{1},y_1) , P_2=(x_{2},y_2), P_3=(x_{3},y_3), P_4=(x_4,y_4) $ равна абсолютной величине (модулю) выражения
$$
frac{1}{2}
left| begin{array}{cc}
x_1-x_3 & y_1-y_3 \
x_2-x_4 & y_2-y_4
end{array}
right| =frac{1}{2} left[(x_1-x_3)(y_2-y_4)-(x_2-x_4)(y_1-y_3)right]
$$
при условии, что стороны не пересекаются.
Площадь $ n_{} $-угольника $ P_{0}P_1dots P_{n-1} P_0 $ с вершинами $ P_0 = (x_{0},y_0) ,dots,
P_{n-1} = (x_{n-1},y_{n-1}) $ равна
абсолютной величине (модулю) выражения
$$
frac{1}{2} sum_{k=1}^{n-2}
left|
begin{array}{lll}
1 & x_0 & y_0 \
1 & x_k & y_k \
1 & x_{k+1} & y_{k+1}
end{array}
right|
$$
при условии, что стороны не пересекаются.
П
Пример. Найти площадь пятиугольника, изображенного на рисунке.
Решение. Имеем: $ P_{0} =(1,2),P_1= (3,4),P_2=(4,1), P_3=(6,5) , P_4=(2,6) $.
$$
S=frac{1}{2}Bigg(
left| begin{array}{ccc}
1& 1 & 2 \
1& 3 & 4 \
1& 4 & 1
end{array}
right| +
left| begin{array}{ccc}
1& 1 & 2 \
1& 4 & 1 \
1& 6 & 5
end{array}
right|
+
left| begin{array}{ccc}
1& 1 & 2 \
1& 6 & 5 \
1 & 2 & 6
end{array}
right|
Bigg) =
$$
$$
=frac{1}{2}(-8+14+17)=frac{23}{2} .
$$
Геометрический смысл суммирования будет более понятен, если перенумеровать точки, сделав стартовой $ P_{1} $: слагаемые в сумме
$$
frac{1}{2}Bigg(
left| begin{array}{ccc}
1& 3 & 4 \
1& 4 & 1 \
1& 6 & 5
end{array}
right| + left| begin{array}{ccc}
1& 3 & 4 \
1& 6 & 5 \
1& 2 & 6
end{array}
right| +
left| begin{array}{ccc}
1& 3 & 4 \
1& 2 & 6 \
1 & 1 & 2
end{array}
right| Bigg) = frac{1}{2}(10+7+6)
$$
теперь отвечают за площади треугольников, на которые разбит пятиугольник точечными линиями.
♦
Площадь параллелограмма в $ {mathbb R}^{2} $ с вершинами $ (0,0), (x_{1},y_1) , (x_2,y_2), (x_1+x_2,y_1+y_2) $ равна абсолютной величине (модулю) определителя
$$
left|
begin{array}{ll}
x_1 & y_1 \
x_2 & y_2 \
end{array}
right| .
$$
П
Пример. Для $ x_{1} =3,y_1=1,x_2=1,y_2=2 $
имеем: $ S_{}=3cdot 2 — 1 cdot 1 = 5 $.
Площадь параллелограмма в $ {mathbb R}^{3} $ с вершинами $ (0,0,0), (x_{1},y_1,z_1) , (x_2,y_2,z_2), (x_1+x_2,y_1+y_2,z_1+z_2) $ равна
$$
sqrt{detleft[left(
begin{array}{lll}
x_1 & y_1 & z_1 \
x_2 & y_2 & z_2 \
end{array}
right)cdot left(
begin{array}{ll}
x_1 & x_2 \
y_1 & y_2 \
z_1 & z_2
end{array}
right)right]
}=sqrt{left|
begin{array}{cc}
x_1^2+y_1^2 + z_1^2 & x_1x_2+y_1y_2+z_1z_2 \
x_1x_2+y_1y_2+z_1z_2 & x_2^2+y_2^2 + z_2^2 \
end{array}
right|
} .
$$
Если применить к определителю произведения матриц теорему Бине-Коши, то получим следующее равенство
$$
detleft[left(
begin{array}{lll}
x_1 & y_1 & z_1 \
x_2 & y_2 & z_2 \
end{array}
right)cdot left(
begin{array}{ll}
x_1 & x_2 \
y_1 & y_2 \
z_1 & z_2
end{array}
right)right]=
left|
begin{array}{ll}
x_1 & y_1 \
x_2 & y_2 \
end{array}
right|^2+left|
begin{array}{ll}
x_1 & z_1 \
x_2 & z_2 \
end{array}
right|^2
+
left|
begin{array}{ll}
y_1 & z_1 \
y_2 & z_2 \
end{array}
right|^2 ,
$$
которое интерпретируется следующим образом: квадрат площади параллелограмма в $ mathbb R^{3} $ равен сумме квадратов площадей его проекций на координатные плоскости. Можно считать этот результат обобщением теоремы Пифагора.
Объемы
тетраэдра
Объем тетраэдра в $ mathbb R^{3} $ с вершинами $ P_1= (x_{1},y_1,z_1) ,P_2=(x_2,y_2,z_2) , P_3=(x_3,y_3,z_3) , P_4=(x_4,y_4,z_4) $ равен абсолютной величине (модулю) выражения
$$
frac{1}{6}
left|
begin{array}{llll}
1 & x_1 & y_1 & z_1 \
1 & x_2 & y_2 & z_2 \
1 & x_3 & y_3 & z_3 \
1 & x_4 & y_4 & z_4
end{array}
right| .
$$
Формула Тартальи (Кэли-Менгера) для квадрата объема тетраэдра через длины его ребер:
$$
V^2=frac{1}{288}
left|
begin{array}{ccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 1 & 0
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Интересно было бы посмотреть, как эта формула выглядела в оригинале у Тартальи, если аппарат определителей был придуман лет на 250 позже…
=>
Если точки $ P_1,P_2,P_3,P_4 $ компланарны, т.е. тетраэдр вырождается в плоский четырехугольник, то формула Тартальи дает связь между сторонами четырехугольника и его диагоналями:
$$
left|
begin{array}{ccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & |P_2P_4|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & |P_2P_4|^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 1 & 0
end{array}
right|=0 , .
$$
Применение тождества Сильвестра дает (в обозначениях рисунка):
$$
left|
begin{array}{cccc}
0 & |P_2P_3|^2 & d_2^2 & 1 \
|P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
d_2^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| cdot
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & d_2^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|
=
$$
$$
=
left|
begin{array}{cccc}
|P_1P_2|^2 & 0 & d_2^2 & 1 \
d_1^2 & |P_2P_3|^2 & |P_3P_4|^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|^2 , .
$$
Откуда получаем формулу
$$
2, d_1^2 d_2^2=(|P_1P_2|^2+|P_2P_3|^2+|P_3P_4|^2+|P_1P_4|^2-d_2^2) d_2^2+
$$
$$
+(|P_3P_4|^2-|P_2P_3|^2)(|P_1P_2|^2-|P_1P_4|^2)+
$$
$$
+left{
left|
begin{array}{cccc}
0 & |P_2P_3|^2 & d_2^2 & 1 \
|P_2P_3|^2 & 0 & |P_3P_4|^2 & 1 \
d_2^2 & |P_3P_4|^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right| cdot
left|
begin{array}{cccc}
0 & |P_1P_2|^2 & |P_1P_4|^2 & 1 \
|P_1P_2|^2 & 0 & d_2^2 & 1 \
|P_1P_4|^2 & d_2^2 & 0 & 1 \
1 & 1 & 1 & 0
end{array}
right|right}^{1/2} , ,
$$
позволяющую определить длину диагонали $ d_1 $ четырехугольника $ P_1P_2P_3P_4 $ через длину его второй диагонали и длины сторон.
Из формулы Герона далее следует:
$$
2,d_1^2 d_2^2=(|P_1P_2|^2+|P_2P_3|^2+|P_3P_4|^2+|P_1P_4|^2-d_2^2) d_2^2+
$$
$$
+ (|P_2P_3|^2-|P_3P_4|^2)(|P_1P_2|^2-|P_1P_4|^2)+
$$
$$
+16, S_{triangle P_1P_2P_3} S_{triangle P_1P_3P_4} , .
$$
Объем симплекса в $ mathbb R_{}^{n} $ с вершинами в
$$ P_1=(x_{11},x_{12},dots,x_{1n}) ,P_2=(x_{21},x_{22},dots,x_{2n}) , dots ,P_n=(x_{n1},x_{n2},dots,x_{nn}),P_{n+1}=(x_{n+1,1},x_{n+1,2},dots,x_{n+1,n}) , $$
т.е. тела, заданного уравнениями
$$
left{ X=sum_{j=1}^{n+1} alpha_j P_j big| , alpha_1ge 0,dots alpha_{n+1} ge 0, sum_{j=1}^{n+1} alpha_j =1 right}
$$
равен абсолютной величине (модулю) выражения
$$
frac{1}{n!}left| begin{array}{cllll}
1 & x_{11}& x_{12} &dots & x_{1n} \
1 & x_{21}& x_{22} & dots & x_{2n} \
vdots & & & & vdots \
1 & x_{n1}& x_{n2}& dots & x_{nn} \
1 & x_{n+1,1} & x_{n+1,2} & dots & x_{n+1,n}
end{array}
right| .
$$
Формула Кэли-Менгера для квадрата объема симплекса через длины его ребер:
$$
V^2=frac{(-1)^{n-1}}{2^n(n!)^2}
left|
begin{array}{cccccc}
0 & |P_1P_2|^2 & |P_1P_3|^2 & dots & |P_1P_{n+1}|^2 & 1 \
|P_1P_2|^2 & 0 & |P_2P_3|^2 & dots & |P_2P_{n+1}|^2 & 1 \
|P_1P_3|^2 & |P_2P_3|^2 & 0 & dots & |P_3P_{n+1}|^2 & 1 \
dots & & & & & dots \
|P_1P_{n+1}|^2 & |P_2P_{n+1}|^2 & |P_3P_{n+1}|^2 & dots & 0 & 1 \
1 & 1 & 1 & dots & 1 & 0
end{array}
right| .
$$
В частном случае: объем пирамиды
$$
left{ X=(x_1,dots,x_n) in mathbb R^n Big|
sum_{j=1}^nfrac{x_j}{a_j} le 1, x_1 ge 0,dots, x_n ge 0 right} quad npu quad a_1>0,dots,a_n>0
$$
равен
$$
frac{1}{n!}prod_{j=1}^n a_j .
$$
параллелепипеда
Объем $ n_{} $-мерного параллелепипеда в $ {mathbb R}^{n} $, построенного на вершинах
$$ (0,0,dots,0), (x_{11},x_{12},dots,x_{1n}) ,(x_{21},x_{22},dots,x_{2n}) , dots ,(x_{n1},x_{n2},dots,x_{nn}), $$
равен абсолютной величине (модулю) определителя
$$
left| begin{array}{cccc}
x_{11}& x_{12} &dots & x_{1n} \
x_{21}& x_{22} & dots & x_{2n} \
dots & & & dots \
x_{n1}& x_{n2}& dots & x_{nn}
end{array}
right| .
$$
Доказательство
☞
ЗДЕСЬ.
Объем $ m_{} $-мерного параллелепипеда в $ {mathbb R}^{n} $, построенного на вершинах
$$ (0,0,dots,0), (x_{11},x_{12},dots,x_{1n}) ,(x_{21},x_{22},dots,x_{2n}) , dots , (x_{m1},x_{m2},dots,x_{mn}), $$
равен
$$
sqrt{det(Xcdot X^{top}}) npu X=
left( begin{array}{cccc}
x_{11}& x_{12} &dots & x_{1n} \
x_{21}& x_{22} & dots & x_{2n} \
dots & & & dots \
x_{m1}& x_{m2}& dots & x_{mn}
end{array}
right) .
$$
Здесь $ {}^{top} $ означает транспонирование.
Объем $ n_{} $-мерного параллелепипеда, ограниченного плоскостями
$$
a_{j1}x_1+a_{j2}x_2+dots+a_{jn}x_n= pm h_j npu j in {1,dots, n }
$$
равен
$$
frac{2^n displaystyle prod_{j=1}^n h_j}{det[a_{jk}]_{j,k=1}^n} .
$$
эллипсоида
Объем $ n_{} $-мерного эллипсоида, ограниченного поверхностью
$$
(x_1,x_2,dots ,x_n)left( begin{array}{cccc}
a_{11} & a_{12} & dots & a_{1n} \
a_{12} & a_{22} & dots & a_{2n} \
dots & & & dots \
a_{1n} & a_{2n} & dots & a_{nn}
end{array}
right)
left(
begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) =1
$$
(квадратичная форма, стоящая в левой части, положительно определена) равен
$$
frac{pi^{n/2}}{Gamma(frac{n}{2}+1)} frac{1}{sqrt{det [a_{jk}]_{j,k=1}^n}} .
$$
Здесь $ Gamma_{} $ обозначает гамма-функцию, при вычислениях значений которой в последней формуле достаточно пользоваться следующими ее свойствами:
$$Gamma left(frac{1}{2}right)=sqrt{pi}, Gamma(1)=Gamma(2)=1, Gamma(x+1)=xGamma(x) npu forall x >0, Gamma(n+1)=n! npu forall n in {mathbb N} . $$
П
Пример. Площадь, ограниченная эллипсом
$$ a_{11}x_{1}^2+2a_{12}x_1x_2 + a_{22}x_2^2=1 , ,$$
вычисляется по формуле
$$ frac{pi}{sqrt{a_{11}a_{22}-a_{12}^2}} . $$
Объем фигуры, ограниченной эллипсоидом
$$
(x_1,x_2,x_3)left( begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array}
right)
left(
begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right) =1
$$
равен
$$
frac{4}{3} frac{pi}{sqrt{left| begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array}
right|
}} .
$$
Объем фигуры, ограниченной четырехмерным эллипсоидом (в записи, аналогичной предыдущей) –
$$ frac{pi^2}{2sqrt{det(A)}} . $$
Классификация алгебраических кривых и поверхностей
Источники
[1]. Uspensky J.V. Theory of Equations. New York. McGraw-Hill. 1948
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Посчитать площадь треугольника с помощью матрицы
|
|
21/12/10 |
Вот есть координаты: (3, -11), (-11, 4), (18, 13)
|
|
|
|
|
Tlalok |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
14/03/10 |
Что именно Вам не понятно?
|
||
|
|
|||
|
mihailm |
Re: Посчитать площадь треугольника с помощью матрицы
|
|
19/05/10 |
про векторное произведение слышали?
|
|
|
|
|
gris |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
13/08/08 |
Теорию можно и полезно вывести самому.
|
||
|
|
|||
|
VAL |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
27/06/08 |
А еще можно забыть не только про векторное произведение, но даже про вектора. Впишите Ваш треугольник в прямоугольник, стороны которого параллельны координатным осям. Площадь этого прямоугольника, очевидно, равна
|
||
|
|
|||
|
ewert |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
11/05/08 |
Остается вычесть площади трех прямоугольных треугольников. Во-первых, тут есть некоторый элемент жульничества: а что, если вершины расположены иначе?… Но это я так, ладно. Во-вторых, если уж выводить по-сермяжному, то всё гораздо проще. Проводим горизонтальную линию из средней по высоте вершины, рассекающую треугольник на два треугольничка — верхний и нижний. Высоты этих треугольничков нам известны. А общее основание легко находится, скажем, из уравнения той стороны большого треугольника, в которую оно (основание) упирается; ну или, что то же, можно найти горизонтальную координату точки искомой точки пересечения из пропорции, определяемой известными вертикальными координатами трёх точек. И единственный нетривиальный момент во всём этом (при любом подходе) — это угадать в полученном простеньком выражении тот самый определитель.
|
||
|
|
|||
|
VAL |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
27/06/08 |
Остается вычесть площади трех прямоугольных треугольников. Во-первых, тут есть некоторый элемент жульничества: На «некий фокус» согласен. На «жульничество» — нет. Цитата: а что, если вершины расположены иначе?… Все равно получится определитель. Правда, случаи перебирать долго. Цитата: Во-вторых, если уж выводить по-сермяжному, то всё гораздо проще. Проводим горизонтальную линию из средней по высоте вершины, рассекающую треугольник на два треугольничка — верхний и нижний… Можно и так.
|
||
|
|
|||
|
mihailm |
Re: Посчитать площадь треугольника с помощью матрицы
|
|
19/05/10 |
Еще можно предложить формулу Пика)) правда там определителей нет
|
|
|
|
|
nnosipov |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
20/12/10 |
Вот простой практический способ. Нарисуем на клетчатой бумаге параллелограмм в два раза большей площади. Вырежем его, а затем разрежем его по линиям сетки на мелкие кусочки. А потом будем собирать пазл в виде какого-нибудь прямоугольника. Собравши, посчитаем его площадь по всем известной школьной формуле. Вот и всё. И никаких определителей. Зачем они вообще нужны?
|
||
|
|
|||
|
ewert |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
11/05/08 |
И никаких определителей. Зачем они вообще нужны? Они нужны просто по условию задачи. Автору, если я правильно понял, начальство приказало: кровь из носу — но чтоб через определители. А с начальством не спорят. Если у того начальства для своих бздыков есть хоть какие-то основания; а тут — в общем, да, хоть какие-то, но есть. А вот пазлствовать в ситуации, когда есть шаблонные и при том вполне прозрачные подходы — на мой взгляд, не вполне хорошо.
|
||
|
|
|||
|
nnosipov |
Re: Посчитать площадь треугольника с помощью матрицы
|
||
20/12/10 |
А вот пазлствовать в ситуации, когда есть шаблонные и при том вполне прозрачные подходы — на мой взгляд, не вполне хорошо. Да это шутка была. А определители пусть учит, вдруг да пригодятся.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Пусть точки A(x1;y1), B(x2;y2), C(x3;y3) – вершины треугольника, тогда площадь треугольника выражается формулой
В формуле правая сторона — это определитель второго порядка.
Площадь треугольника является положительной величиной и поэтому перед определителем берём знак «плюс», в случае, если значение положительно, и минус в противном случае, то есть отрицательно.
Примечание
Если вершина C треугольника совпадает с началом координат, то есть x3=y3=0, то формула площади треугольника примет види вычисляется как определитель второго порядка
Пример
Найти площадь треугольника с вершинами A(2;-4), B(-5;-6) и C(1;3)
Решение
Пусть примем A за первую вершину, B — за вторую и C — за третью, тогда находим:
,так как получился отрицательный знак, следовательно перед определителем берём знак «минус»
[S = ( — frac{1}{2})cdot( — 51) = 25,5]
Если вершины треугольника переобозначим немного в другом порядке, допустим, первой вершиной A, второй вершиной C и третьей вершиной B, тогда получим выражение:
В этом случае, необходимо взять знак «плюс« и получим снова площадь треугольника S=25,5
3648









 . Остается вычесть площади трех прямоугольных треугольников. Площадь первого равна
. Остается вычесть площади трех прямоугольных треугольников. Площадь первого равна  . И т.д. После приведения подобных неожиданно обнаружится, что у Вас с точностью до знака получилось разложение детерминанта
. И т.д. После приведения подобных неожиданно обнаружится, что у Вас с точностью до знака получилось разложение детерминанта