в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 467 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 …
Добавить в вариант
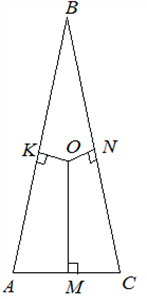
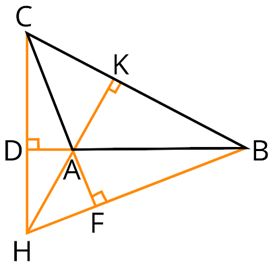
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36.
Укажите номера верных утверждений.
1) В любую равнобедренную трапецию можно вписать окружность.
2) Диагональ параллелограмма делит его углы пополам.
3) Площадь прямоугольного треугольника равна половине произведения его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 3. Найдите площадь треугольника ABC, если AB = 15.
В равнобедренной трапеции ABCD боковые стороны равны меньшему основанию BC. К диагоналям трапеции провели перпендикуляры BH и CE. Найдите площадь четырёхугольника BCEH, если площадь трапеции ABCD равна 36 .
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Если утверждений несколько, запишите их номера в порядке возрастания.
Источник: Банк заданий ФИПИ
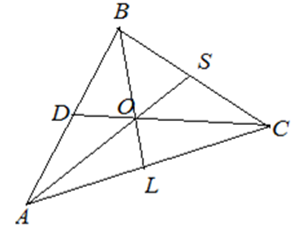
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOB.
Источник: Банк заданий ФИПИ
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
Источник: Банк заданий ФИПИ
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Источник: Банк заданий ФИПИ
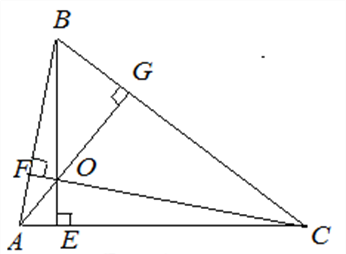
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 4, тангенс угла BAC равен 0,75. Найдите радиус вписанной окружности треугольника ABC.
Источник: Банк заданий ФИПИ
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Источник: Банк заданий ФИПИ
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Источник: Банк заданий ФИПИ
Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
Источник: Банк заданий ФИПИ
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Источник: Банк заданий ФИПИ
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
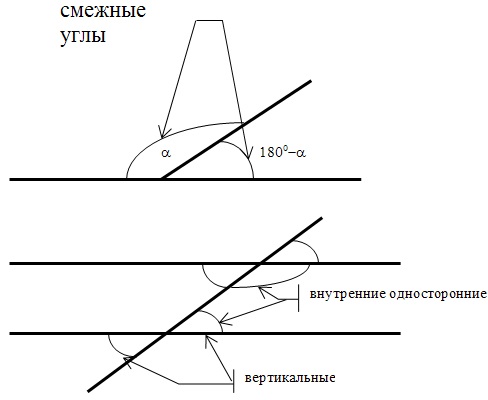
2) Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равна 180° , то эти прямые параллельны.
3) Площадь треугольника не превышает произведения двух его сторон.
Источник: Банк заданий ФИПИ
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Источник: Банк заданий ФИПИ
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Источник: Банк заданий ФИПИ
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Источник: Банк заданий ФИПИ
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
Источник: Банк заданий ФИПИ
Всего: 467 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 | 121–140 …
Площадь треугольника
Задача
1. В
треугольнике одна из сторон равна 27, а опущенная на нее высота – 11. Найдите
площадь треугольника.
Решение: Площадь треугольника = ½
основания*высоту
Пл.треугольника
= ½*27*11=148,5
Ответ:
148,5
Задача
2. Два
катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого
треугольника.
Решение:
Пл.прямоугольного
треуг. = половине произведения катетов.
Пл.прямоуг.треуг.=(4*9):2=36:2=18
Ответ: 18
Задача
3. Периметр
равнобедренного треугольника равен 144, а основание – 64. Найдите площадь
треугольника.
Решение:
1) Т.к.
Треугольник равнобедренный, из этого следует, что две стороны равны АС=СВ,
найдем длину этих 
АС=СВ=(144-64):2=40.
2)
Формула Герона:
Найдем
полупериметр, т.к. периметр = 144, то полупериметр = 144:2=72.
Ответ: 768
Задача
4. Найдите
площадь треугольника.
Решение: Для формулы нам необходимо
знать основание и высоту
Основание=32+11=43.
Высота
= 60.
S треуг.= ½*60*43=1290
Ответ: 1290
32+11=43
Задача
5.
 |
6
3
Решение:
Задачу
можно решить по формуле Пика, можно по формуле площади треугольника.
Считаем
по клеточкам основание =3, высота = 6.
S=1/2*3*6= 9
Ответ: 9
Задачи
для самостоятельного решения:
1)
В
треугольнике одна из сторон равна 14, а опущенная на нее высота – 31. Найдите
площадь треугольника.
2)
Сторона
треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите
площадь этого треугольника.
3)
Два катета прямоугольного треугольника равны 7 и 12. Найдите площадь этого
треугольника.
4) Два катета
прямоугольного треугольника равны 18 и 7. Найдите площадь этого треугольника.
5) Периметр
равнобедренного треугольника равен 162, а основание – 72. Найдите площадь
треугольника.
6) Найдите площадь
треугольника
7) Найдите площадь
треугольника

9) Найдите площадь треугольника
10)
11) 
12)
13)
14)
16)
Проверить решение можно по ссылке:
https://onlinetestpad.com/hnl6ukjjcnpgo
Простой ответ, что включено в 15 задание ОГЭ по математике
Тема треугольников в ОГЭ по математике охватывает все важные определения и формулы площади различных фигур. Важно знать и уметь применять свойства треугольников, а также ориентироваться в понятиях синуса, косинуса, тангенса прямоугольного треугольника.
Прямоугольные треугольники – разбор 15 задания ОГЭ по математике
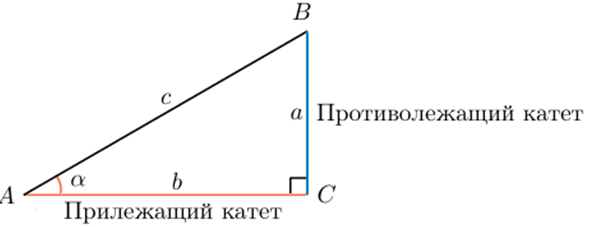
Треугольник называется прямоугольным, если один из его углов прямой, то есть равен 90º. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая против прямого угла — гипотенуза.
Свойства прямоугольного треугольника:
- Сумма острых углов треугольника равна 90º.
- Гипотенуза прямоугольного треугольника больше каждого из катетов.
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
- Две высоты прямоугольного треугольника совпадают с его катетами.
- Центр описанной окружности прямоугольного треугольника лежит
в середине гипотенузы. - Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
Понятие синуса, косинуса, тангенса прямоугольного треугольника – задание 15 ОГЭ математика 2023 теория
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что-то же самое, отношение косинуса к синусу):
Основное тригонометрическое тождество связывает синус и косинус одного и того же угла. Сформулируем его: для любого угла справедливо:
Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника помогают сравнивать углы треугольника, зная соотношение его сторон, и наоборот.
Теорема (соотношения между сторонами и углами треугольника)
В треугольнике:
1) против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
Теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
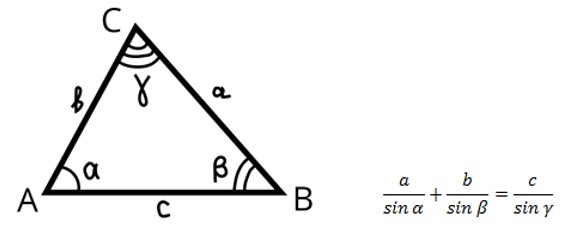
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
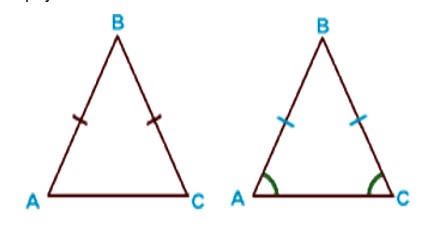
Равнобедренный треугольник – ОГЭ математика
Равнобедренный треугольник — треугольник, у которого равны две стороны. Например: AB = BC — боковые стороны; AC — основание равнобедренного треугольника.
Свойства равнобедренного треугольника:
- в равнобедренном треугольнике углы при основании равны;
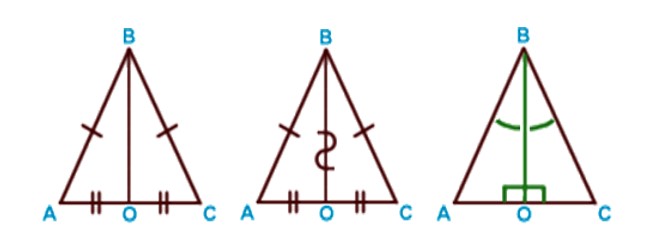
- в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
AB=BC (равнобедренный треугольник), AO=OC (BO — медиана), BO — общая сторона ΔABO и ΔCBO. ΔABO = ΔCBO по 3 признаку.
Следовательно: ∠ ABO = ∠ CBO. BO — биссектриса. ∠AOC — развернутый угол = 180°.
BO — высота.
- В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
- В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Признаки равнобедренного треугольника:
1) если в треугольнике два угла равны, то он равнобедренный;
2) если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
3) если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
4) если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
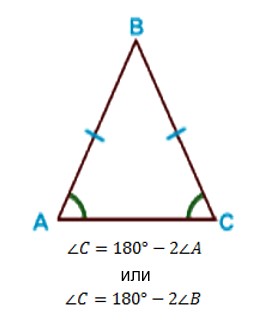
Свойство углов равнобедренного треугольника
В равнобедренном треугольнике углы при основании равны.
Поскольку в любом треугольнике сумма углов равна 180°, то угол, противоположный основанию выражается следующим образом:
где ∠ A и ∠ B — углы при основании равнобедренного треугольника.
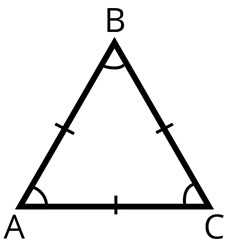
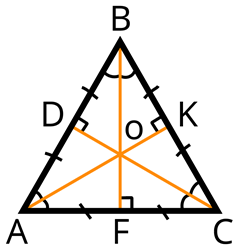
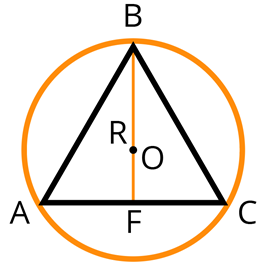
Равносторонний треугольник
Равносторонним треугольником называется треугольник, у которого все стороны равны.
Свойства равностороннего треугольника
1) Все углы равностороннего треугольника равны по 60º.
2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:
AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой: AK=BF=CD
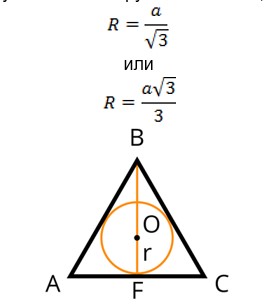
Если a — сторона треугольника, то
3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника
и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин: AO:OK=BO:OF=CO:OD=2:1
5) Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности: BO=R,
6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности: OF=r
или
7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.

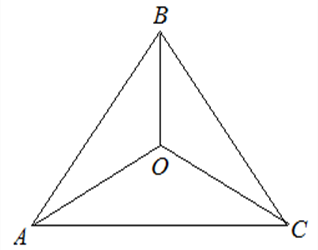
Замечательные точки треугольника – ОГЭ математика задание 15
Первая замечательная точка треугольника
Точка пересечения биссектрис.
Эта точка является центром вписанной в треугольник окружности и всегда находится внутри треугольника. Данная точка равноудалена от сторон треугольника.
Вторая замечательная точка треугольника
Точка пересечения серединных перпендикуляров сторон треугольника.
Эта точка — центр описанной около треугольника окружности, находится в треугольниках с острыми углами, вне треугольника с тупым углом и на гипотенузе прямоугольного треугольника. Данная точка равноудалена от всех вершин треугольника.
Третья замечательная точка треугольника
Точка пересечения медиан.
Теорема
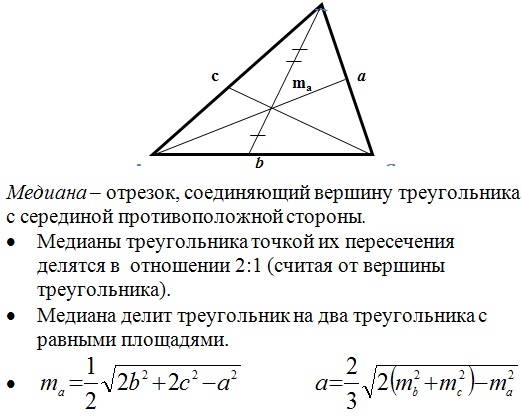
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану
в отношении 2:1, считая от вершины.
Точка пересечения медиан является центром тяжести треугольника.
Четвёртая замечательная точка треугольника
Точка пересечения высот треугольника.
Теорема
Высоты треугольника или их продолжения пересекаются в одной точке.
Точку пересечения высот называется ортоцентром треугольника.
Высоты в тупоугольных треугольниках
В отличие от медианы или биссектрисы, высота треугольника может быть расположена как внутри треугольника, так и вне его.
В тупоугольном треугольнике внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла.
Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника.
AK — высота, проведенная к стороне BC.
BF — высота, проведенная к продолжению стороны АС.
CD — высота, проведенная к продолжению стороны AB.
Точка пересечения высот тупоугольного треугольника также находится вне треугольника:
Точка H — ортоцентр треугольника ABC.
Площадь треугольника
Первая формула
Площадь треугольника равна половине произведения длины основания и высоты, опущенной на это основание.
Формула вторая
Площадь треугольника равна половине произведения его соседних сторон на синус угла между ними.
Формула Герона (третья)
Формула четвёртая
где r — радиус вписанной окружности
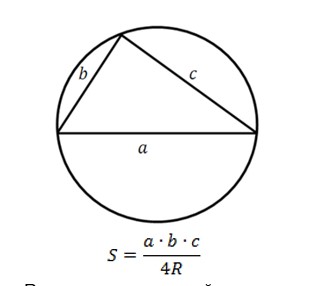
Формула пятая
где R — радиус описанной окружности.
Прототипы задания 15 ОГЭ математика 2023
Задача 1
Сторона равностороннего треугольника равна . Найдите высоту этого треугольника.
Решение
Так как треугольник ABC равносторонний, то его высота BH является и медианой, и биссектрисой. Тогда треугольник ABH — прямоугольный. Тогда:
Ответ: 24.
Задача 2
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH=64, CH=16. Найдите cosB.
Решение
Из треугольника ABH по определению косинуса:
Ответ: 0,8.
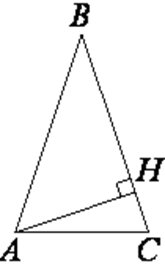
Задача 3
В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
Решение
Треугольник ABC — прямоугольный. Таким образом
Ответ: 30.
Задача 4
Площадь прямоугольного треугольника равна
Один из острых углов равен 30°. Найдите длину гипотенузы.
Решение
Пусть x — длина катета, лежащего против угла в 30°, тогда гипотенуза равна 2x, второй катет равен
Площадь прямоугольного треугольника равна половине произведения катетов.
Следовательно, длина гипотенузы, равна 16.
Ответ: 16.
В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №15
Так как задания №16 основаны на теории по теме “треугольники”, рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
Медиана:
Теперь вспомним основные формулы нахождения площади треугольника:
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников – равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник – треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник – треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
Прямоугольный треугольник:
Задание 15OM21R
В треугольнике АВС известно, что угол ВАС равен 840, АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 840:2=420
Ответ: 42
pазбирался: Даниил Романович | обсудить разбор
Задание OM1611o
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 – 123 = 57°
Из второго – что ∠BCA = ∠BAC = 57°
Ответ: 57
pазбирался: Даниил Романович | обсудить разбор
Задание OM1610o
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22
pазбирался: Даниил Романович | обсудить разбор
Задание OM1609o
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20
pазбирался: Даниил Романович | обсудить разбор
Задание OM1608o
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18
pазбирался: Даниил Романович | обсудить разбор
Задание OM1607o
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30
pазбирался: Даниил Романович | обсудить разбор
Задание OM1606o
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Для решения необходимо вспомнить определение медианы.
Медиана – отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28
pазбирался: Даниил Романович | обсудить разбор
Задание OM1605o
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 – 23 = 67°
Ответ: 67
pазбирался: Даниил Романович | обсудить разбор
Задание OM1604o
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m – медиана в равностороннем треугольнике, а a – сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15
pазбирался: Даниил Романович | обсудить разбор
Задание OM1603o
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Если в треугольнике две стороны равны – значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 – 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29
pазбирался: Даниил Романович | обсудить разбор
Задание OM1602o
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия – это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC – третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32
pазбирался: Даниил Романович | обсудить разбор
Задание OM1601o
В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Для решения этого задания достаточно знать правило – сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 – 73 – 48 = 59
Ответ: 59
pазбирался: Даниил Романович | обсудить разбор
Площадь треугольника требуется уметь находить, чтобы успешно решить модуль “Геометрия” в ОГЭ. Умение находить площадь треугольника является одним из основополагающих умений в геометрии. Для того, чтобы находить площадь треугольника в заданиях ОГЭ – нужно иметь представления о том, по каким формулам вообще находится площадь треугольника. Ниже мы приводим их все, а также даем анализ того, как часто встретятся вам эти формулы при выполнении заданий по геометрии в ОГЭ.
Задачи самые разнообразные, как и треугольники, как и методы их решения. Однако, для того, чтобы решать такие задачи, нам понадобятся формулы и общие сведения.
Площадь треугольника. Формулы. Задачи.
1. Формула нахождения площади треугольника по двум сторонам и углу между ними
Эта формула считается общей, ее очень часто используют, особенно если в треугольнике известен какой-либо угол. Ее кратко называют так “площадь треугольника через синус”. Итак, посмотрите на чертеж – нам дан треугольник ABC, известны две его стороны и угол между ними. Тогда площадь треугольника находится по формуле:
 Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задача 1. Найдите площадь треугольника, две стороны которого равны 19 и 18, а угол между ними равен 300. Решение. Используем формулу площади треугольника через синус: Ответ: 85,5 Задача 2. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 0 . Боковая сторона треугольника равна 2. Найдите площадь этого треугольника. Решение. Нарисуем треугольник. Обозначим его вершины – A, B, C. Значит, нам дано: <ABC=1500. AB=BC=2. Тогда для того, чтобы найти площадь треугольника, воспользуемся формулой нахождения площади треугольника по двум сторонам и углу между ними:

Ответ: 1.
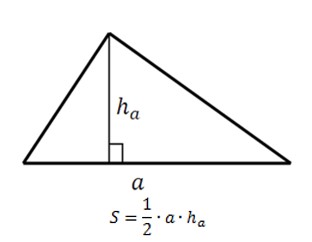
2. Площадь треугольника через высоту.
Самая любимая школьниками формула определения площади треугольника – определение площади через высоту. В этой формуле всего нужно знать две величины – основание треугольника и высоту проведенную из вершины треугольника к этому основанию – смотрите рисунок.
Очень удобная формула для определения любого треугольника, если известны любые три его размера.
3. Площадь равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Нахождение площади равнобедренного треугольника ничем не отличается от нахождения площади обыкновенного треугольника, разве что формула площади равнобедренного треугольника несколько упрощается. Например, если дана боковая сторона треугольника и угол при вершине, то формула нахождения площади будет выглядеть так:
Вообще говоря, нет необходимости выводить и тем более запоминать некую мифическую формулу площади равнобедренного треугольника. Нужно просто помнить, что равнобедренный треугольник всего лишь частный случай общего, обыкновенного треугольника и все те формулы, которые применимы для нахождения площади треугольника, будут применимы и для равнобедренного треугольника.
Гораздо важнее не забыть свойства равнобедренного треугольника – высота (перпендикуляр), проведенная к основанию равнобедренного треугольника, есть медиана (делит основание пополам), биссектриса (делит угол напротив основания пополам). Углы при основании равнобедренного треугольника равны.
4. Площадь треугольника по координатам вершин
Никакой волшебной формулы тут нет – вы просто, используя координаты вершин, находите длины сторон треугольника, а затем подставляете их в формулу Герона.
5. Формула Герона для нахождения площади треугольника
,
где p – полупериметр треугольника, который находится по формуле:
а, b и c – стороны треугольника.
Таким образом, зная формулы, найти площадь треугольника не составит никакого труда.
Как находить площадь треугольника в заданиях ОГЭ.
В заданиях ОГЭ обычно площадь треугольника просят найти с помощью самой простой формулы – через основание и высоту.
Очень и очень редко встречается задача нахождения площади треугольника через две стороны и синус угла между ними, а уж формула Герона вообще не встречается, разве что вы можете ее использовать, если она вам очень нравится, да и то – в задачах второй части ОГЭ.














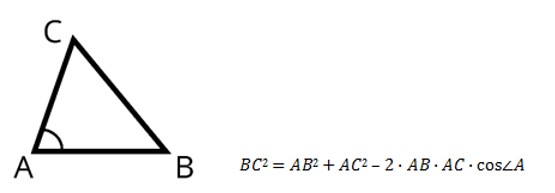
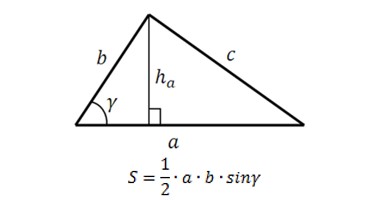
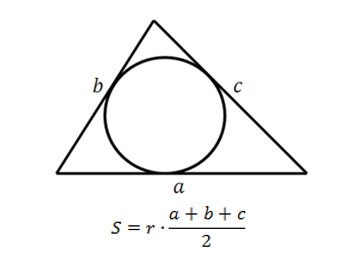
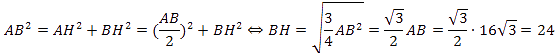
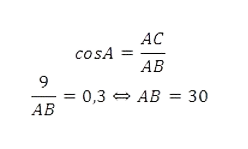
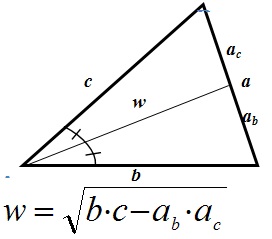
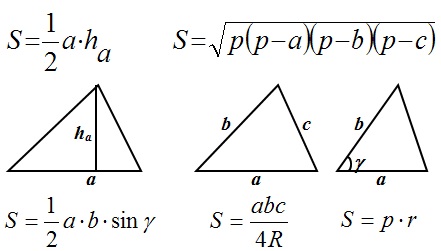
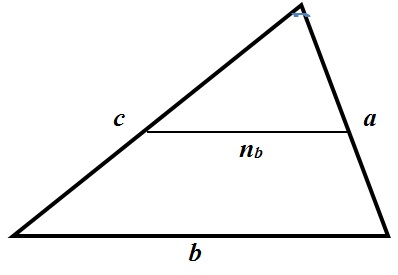
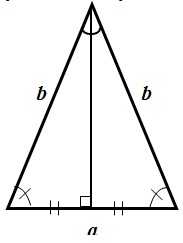
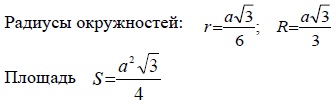



 Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.
Задачи на определение площади треугольника при заданных сторонах треугольника и углу между ними.

