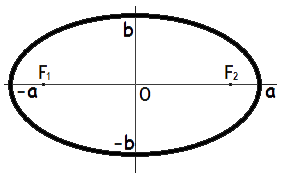Теорема Пифагора
Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².
Доказательство
Доказательство теоремы Пифагора, используя алгебру
Нужно доказать, что c² = a² + b²:
Это квадрат, в котором есть 4 одинаковых треугольника abc:
- Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: A = (a + b) (a + b);
- Площадь наименьшего квадрата (который находится внутри, под наклоном): c²;
- Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе: 4ab/2 = 2ab;
- Сумма наименьшего квадрата и треугольников: A = c² + 2ab;
- Площадь большого квадрата (A = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:
(a + b) (a + b) = c² + 2ab
a² + 2ab + b² = c² + 2ab
a² + b² = c²
Что и требовалось доказать.
«Пифагоровы штаны на все стороны равны»
Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора
На этой фигуре c — гипотенуза, a и b — катеты.
Проведём перпендикулярную линию к гипотенузе (c):
Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).
- Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
- Делим «Пифагоровы штаны» на 3 похожие фигуры:
- Все 3 треугольника подобны друг другу (A, B, C) и из-за этого «фигуры-домики» также являются подобными.
- Значит соотношение площади A и a² будет одинаковым с площадью B и b², но и с площадью C и c². Т. е.: A/a² = B/b² = C/c² = β (назовём это соотношение греческой буквой бета);
- Площадь каждого треугольника, через площадь каждого из квадратов, равна: A = βa², B = βb², C = βc²;
- Вспомним, что С = А + B, т. е. βc² = βa² + βb², это равно c² = a² + b².
Что и требовалось доказать.
Примеры
Задача 1
На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.
Решение:
Записать формулу
c² = a² + b²
Подставить известные значения
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = √25
x = 5
Ответ: длина гипотенузы равна 5.
Задача 2
Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.
Решение:
Записать формулу
c² = a² + b²
Подставить известные значения
13² = 12² + b²
169 = 144 + b²
169 – 144 = b²
25 = b²
√25 = b
5 = b
Ответ: длина другой стороны треугольника равна 5.
Следствия из теоремы Пифагора
Это основные следствия теоремы:
- В прямоугольном треугольнике гипотенуза всегда больше любого из двух катетов.
- Если применить формулу теоремы Пифагора (c² = a² + b²) и равенство будет верным, (т.е. если квадрат одной стороны равен сумме квадратов двух других сторон), то треугольник прямоугольный.
- Из формулы теоремы Пифагора также можно посчитать любой из катетов: a² = c² − b² либо b² = c² − a².
- Любой косинус (cos) острого угла будет меньше 1.
Кто придумал теорему Пифагора
Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).
Узнайте также, что такое Теорема Виета и Аксиома.
Петр Петрович надел новые штаны и сел на только что покрашеную табуретку. На штанах получилось квадратное пятно зеленого цвета. Длина одной стороны пятна 35 см, а площадь его в 35730 раз меньше центральной площади города, в которой живет Петр Петрович. Узнай площадь этойплощади.
Остались вопросы?
Новые вопросы по предмету Математика
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Формулы площади геометрических фигур
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,p = a + b + c — полупериметр треугольника. 2
Формулы площади квадрата
-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Формулы площади ромба
-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
Формулы площади трапеции
-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a — b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,p = a + b + c + d — полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника
-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ
где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)
Формулы площади круга
-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.
Формулы площади эллипса
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S — Площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.
Пифагоровы штаны
- Пифагоровы штаны
-
Построение «Пифагоровых штанов»
Пифаго́ровы штаны́ (школьн., устар.) — шуточное название одного из доказательств теоремы Пифагора.
История
В старых школьных учебниках приводилось доказательство теоремы через получение равенства суммы площадей квадратов, построенных на катетах прямоугольного треугольника, площади квадрата, построенного на гипотенузе этого треугольника. Построенные на сторонах треугольника и расходящиеся в разные стороны квадраты напоминали покрой мужских штанов, что породило шуточные четверостишия, например:
- Пифагоровы штаны —
- На все стороны равны.
- Чтобы это доказать,
- Нужно снять и показать[1]
или:
- Пифагоровы штаны
- На все стороны равны,
- Потому что Пифагор
- Не ходил три дня во двор.
или:
- Пифагоровы штаны
- На все стороны равны,
- Число пуговиц известно
- Почему в штанах так тесно?
- Потому что хер велик —
- Отвечает ученик.
или:
- Пифагоровы штаны
- На все стороны равны,
- Потому что Пифагор
- Имеет жопу как бугор. (Спальный район Москвы, середина 1980-х)
См. также
- Пифагорово дерево
Примечания
- ↑ Кафедра математики СУНЦ МГУ — школы им. А. Н. Колмогорова :: Вавилов В. В. :: Тезисы лекций по геометрии, 10 класс
Научный юмор
Люди Марк Абрахамс • Эдвард Мёрфи • Сирил Паркинсон • Джон Литлвуд • Герольф Штайнер
Шутки,
примерыЗакон Мёрфи • Закон Паркинсона • Защита диссертации (пьеса) • Парадокс кошки с маслом • Принцип Питера • Закон Старджона • Три закона Кларка • Шнобелевская премия • Эффект гремлина • Сферический конь в вакууме • Математика: Пифагоровы штаны • Химия: Дигидрогена монооксид • Зоология: Ринограденции • Лингвистика: Глокая куздра
Периодика Физики шутят • Флатландия • Анналы невероятных исследований • Журнал невоспроизводимых результатов
В культуре xkcd • Футурама • Пинки и Брейн • Автостопом по Галактике • Понедельник начинается в субботу • Ийон Тихий • Приключения Джимми Нейтрона, мальчика-гения • Теория большого взрыва
Религия Невидимый Розовый Единорог • Летающий Макаронный Монстр • Гуглизм • Копимизм • Разумное падение • Чайник Рассела • Дискордианизм • Боконизм • Церковь НедоМудреца
Категории:
- Элементарная математика
- Сленг
- Научный юмор
- Пифагор
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Пифагоровы штаны» в других словарях:
-
пифагоровы штаны(выдумать) — иноск.: о человеке даровитом Ср. Это несомненности мудрец. В древности он наверное выдумал бы Пифагоровы штаны … Салтыков. Пестрые письма. Пифагоровы штаны (геом.): в прямоугольнике квадрат гипотенузы равняется квадратам катетов (учение… … Большой толково-фразеологический словарь Михельсона
-
Пифагоровы штаны на все стороны равны — Число пуговиц известно. Почему же хую тесно? (грубо) о штанах и мужском половом органе. Пифагоровы штаны на все стороны равны. Чтобы это доказать, надо снять и показать 1) о теореме Пифагора; 2) о широких штанах … Живая речь. Словарь разговорных выражений
-
Пифагоровы штаны выдумать — Пиѳагоровы штаны (выдумать) иноск. о человѣкѣ даровитомъ. Ср. Это несомнѣнности мудрецъ. Въ древности онъ навѣрное выдумалъ бы пиѳагоровы штаны… Салтыковъ. Пестрыя письма. Пиѳагоровы штаны (геом.): въ прямоугольникѣ квадратъ гипотенузы… … Большой толково-фразеологический словарь Михельсона (оригинальная орфография)
-
Пифагоровы штаны — Жарг. шк. Шутл. Теорема Пифагора, устанавливающая соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника. БТС, 835 … Большой словарь русских поговорок
-
Пифагоровы штаны — Шуточное название теоремы Пифагора, возникшее в силу того, что построенные на сторонах прямоугольника и расходящиеся в разные стороны квадраты напоминают покрой штанов. Геометрию я любил… и на вступительном экзамене в университет получил даже от… … Фразеологический словарь русского литературного языка
-
пифагоровы штаны — Шутливое название теоремы Пифагора, устанавливающей соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника, что внешне на рисунках выглядит как покрой штанов … Словарь многих выражений
-
Пифагоровы штаны во все стороны равны — Шутливое доказательство теоремы Пифагора; также в шутку о мешковатых брюках приятеля … Словарь народной фразеологии
-
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ (ЧИСЛО ПУГОВИЦ ИЗВЕСТНО. ПОЧЕМУ ЖЕ ХУЮ ТЕСНО? / ЧТОБЫ ЭТО ДОКАЗАТЬ, НАДО СНЯТЬ И ПОКАЗАТЬ) — присл., груб … Толковый словарь современных разговорных фразеологизмов и присловий
-
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ (ЧИСЛО ПУГОВИЦ ИЗВЕСТНО. ПОЧЕМУ ЖЕ ХУЮ ТЕСНО? / ЧТОБЫ ЭТО ДОКАЗАТЬ, НАДО СНЯТЬ И ПОКАЗАТЬ) — присл., груб … Толковый словарь современных разговорных фразеологизмов и присловий
-
штаны — сущ., мн., употр. сравн. часто Морфология: мн. что? штаны, (нет) чего? штанов, чему? штанам, (вижу) что? штаны, чем? штанами, о чём? о штанах 1. Штаны это предмет одежды, который имеет две короткие или длинные штанины и закрывает нижнюю часть… … Толковый словарь Дмитриева