Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
C# is a general-purpose, modern and object-oriented programming language pronounced as “C Sharp”. In this article, we will see how to calculate the area of a circle in C#.
The area of a circle can be evaluated using the formula:
Area of circle = pi * r * r //where r is the radius of circle
Example 1:
C#
using System;
class Circle
{
static void Main(string[] args)
{
Console.Write("Enter Radius: ");
double rad = Convert.ToDouble(Console.ReadLine());
double area = Math.PI * rad * rad;
Console.WriteLine("Area of circle is: " + area);
}
}
Output:
Code Explanation:
The formula used to calculate the circle area: π * r * r. Where, r is the radius and π is the mathematical constant Pi. We will take the value of radius from the user as input. For π, we can either define a variable and assign it up to a specific decimal place or we can use Math.PI constant that is available in C#.
- The Radius is a double value to keep the radius of the circle.
- The area is double to save the area of the circle.
- The final area is stored in the double area.
- Finally, we are writing down the area of a circle.
Last Updated :
22 Jun, 2022
Like Article
Save Article
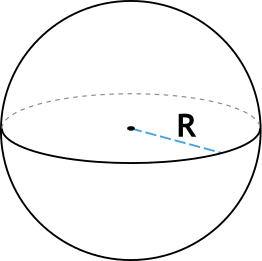
Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее RR — радиус этого шара.
Онлайн-калькулятор площади поверхности шара
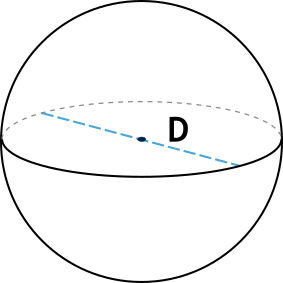
У шара, как и у круга, есть диаметр DD, который по длине в два раза превосходит радиус шара.
D=2⋅RD=2cdot R
Площадь поверхности шара можно найти используя как радиус, так и диаметр шара.
Формула площади поверхности шара по радиусу шара
S=4⋅π⋅R2S=4cdotpicdot R^2
RR — радиус шара.
Шар вписан в куб, диагональ которого dd равна 300sqrt{300} (см.). Найти площадь поверхности шара.
Решение
d=300d= sqrt{300}
Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через aa. Тогда, по теореме Пифагора:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
a=d3a=frac{d}{sqrt{3}}
a=3003=100=10a=frac{sqrt{300}}{sqrt{3}}=sqrt{100}=10
Радиус шара, вписаного в куб равен половине стороны этого куба:
R=a2=102=5R=frac{a}{2}=frac{10}{2}=5
Тогда площадь поверхности шара:
S=4⋅π⋅R2=4⋅π⋅52≈314S=4cdotpicdot R^2=4cdotpicdot 5^2approx314 (см. кв.)
Ответ: 314 см. кв.
Формула площади поверхности шара по диаметру шара
Формулу для площади поверхности шара легко получить через его диаметр, пользуясь соотношением между радиусом и диаметром шара:
S=4⋅π⋅R2=4⋅π⋅(D2)2=π⋅D2S=4cdotpicdot R^2=4cdotpicdotBig(frac{D}{2}Big)^2=picdot D^2
S=π⋅D2S=picdot D^2
DD — диаметр шара.
Диаметр шара равен 10 (см.). Найдите площадь его поверхности.
Решение
D=10D=10
По формуле получаем:
S=π⋅D2=π⋅102≈314S=picdot D^2=picdot 10^2approx314 (см. кв.)
Ответ: 314 см. кв.
Студворк — лучший сайт для заказа контрольных работ!
Тест по теме «Площадь поверхности шара»
Площадь поверхности шара, или как часто неправильно говорят просто площадь шара, вычисляется по очень простой формуле. Но даже простые вещи можно упростить и именно поэтому мы сделали калькулятор, который в режиме онлайн может рассчитать площадь поверхности шара, а также на странице вы найдете формулу для расчета.
Возможно вам дополнительно потребуется рассчитать и объем шара.
Шар — геометрическое тело, состоящее из точек пространства, которые удалены от центра на расстояние, не более заданного. Это расстояние называют радиусом шара.
Содержание:
- калькулятор площади поверхности шара
- формула площади поверхности шара через радиус
- формула площади поверхности шара через диаметр
- формула площади поверхности шара через длину окружности
- примеры задач
Формула площади поверхности шара через радиус
{S = 4pi R^2}
R — радиус шара
Формула площади поверхности шара через диаметр
{S = pi D^2}
D — диаметр шара
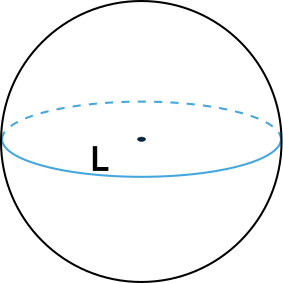
Формула площади поверхности шара через длину окружности
{S = dfrac{L^2}{pi}}
L — длина окружности шара
Примеры задач на нахождение площади поверхности шара
Задача 1
Найдите площадь поверхности шара диаметром 10см.
Решение
Так как в условии дан диаметр шара, мы воспользуемся второй формулой.
S = pi D^2 = pi cdot 10^2 = pi cdot 100 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
калькулятор поможет проверить правильность вычислений.
Задача 2
Найдите площадь поверхности шара, если его радиус равен 5см.
Решение
В этой задаче мы будем использовать первую формулу.
S = 4pi R^2 = 4pi cdot 5^2 = 4pi cdot 25 = 100pi : см^2 approx 314.15927 : см^2
Ответ: 100pi : см^2 approx 314.15927 : см^2
Проверка ответа.
Ваше решение записывайте как комментарий к данной странице (пример оформления).
Решены задачи: 1-22, 24,27 Не решены: 23,25,26,28. Для многих задач есть варианты решений с обсуждениями, смотрите.
Задачи
S2.1. Составить программу:
а) вычисления значения функции y=7x2+3x+6 при любом значении x;
б) вычисления значения функции x=12a2+7a+12 при любом значении а.
S2.2. Дана сторона квадрата. Найти его периметр. — решение.
S2.3. Дан радиус окружности. Найти ее диаметр. — решение.
S2.4. Считая, что Земля — идеальная сфера с радиусом R=6350 км, определить расстояние до линии горизонта от точки В с заданной высотой h=AB над Землей.
S2.5. Дана длина ребра куба. Найти объем куба и площадь его боковой поверхности. — решение
S2.6. Дан радиус окружности. Найти длину окружности и площадь круга.
S2.7. Даны два целых числа. Найти: а) их среднее арифметическое; б) их среднее геометрическое.
S2.8. Известны объем и масса тела. Определить плотность материала этого тела.
S2.9. Известны количество жителей в государстве и площадь его территории. Определить плотность населения в этом государстве.
S2.10. Составить программу решения линейного уравнения ax+b=0 (a ≠ 0).
S2.11. Даны катеты прямоугольного треугольника. Найти его гипотенузу.
S2.12. Найти площадь кольца по заданным внешнему и внутреннему радиусам.
S2.13. Даны катеты прямоугольного треугольника. Найти его периметр.
S2.13А. Даны два числа. Найти среднее арифметическое и среднее геометрическое их модулей.
S2.14. Даны основания и высота равнобедренной трапеции. Найти ее периметр.
S2.14А. Даны стороны прямоугольника. Найти его периметр и длину диагонали.
S2.15. Даны два числа. Найти их сумму, разность, произведение, а также частное от деления первого числа на второе.
S2.16. Даны длины сторон прямоугольного параллелепипеда. Найти его объем и площадь боковой поверхности.
S2.17. Известны координаты на плоскости двух точек. Составить программу вычисления расстояния между ними.
S2.18. Даны основания и высота равнобедренной трапеции. Найти периметр трапеции.
S2.19. Даны основания равнобедренной трапеции и угол при большем основании. Найти площадь трапеции.
S2.20. Треугольник задан координатами своих вершин. Найти периметр и площадь треугольника.
S2.21. Выпуклый четырехугольник задан координатами своих вершин. Найти площадь этого четырехугольника как сумму площадей треугольников.
S2.22. Известна стоимость 1 кг конфет, печенья и яблок. Найти стоимость всей покупки, если купили x кг конфет, у кг печенья и z кг яблок.
S2.23. Известна стоимость монитора, системного блока, клавиатуры и мыши. Сколько будут стоить 3 компьютера из этих элементов? N компьютеров?
S2.24. Возраст Тани — X лет, а возраст Мити — Y лет. Найти их средний возраст, а также определить, на сколько отличается возраст каждого ребенка от среднего значения. — решение
S2.25. Два автомобиля едут навстречу друг другу с постоянными скоростями V1 и V2 км/час. Определить, через какое время автомобили встретятся, если расстояние между ними было S км.
S2.26. Два автомобиля едут друг за другом с постоянными скоростями V1 и V2 км/час (V1>V2). Определить, какое расстояние будет между ними через 30 минут после того, как первый автомобиль опередил второй на S км.
S2.27. Известно значение температуры по шкале Цельсия. Найти соответствующее значение температуры по шкале: а) Фаренгейта; б) Кельвина. Для пересчета по шкале Фаренгейта необходимо исходное значение температуры умножить на 1,8 и к результату прибавить 32, а по шкале Кельвина абсолютное значение нуля соответствует 273,15 градуса по шкале Цельсия.
S2.28. У американского писателя-фантаста Рэя Бредбери есть роман «450 градусов по Фаренгейту». Какой температуре по шкале Цельсия соответствует указанное в названии значение? (См. предыдущую задачу).
Пример оформления:
Задача S2.3
static void Main(string[] args)
{
Console.Write("Введите радиус окружности : ");
double r = Convert.ToDouble(Console.ReadLine());
double d = 2 * r;
Console.WriteLine("Диаметр окружности = {0}", d);
}
NEW: Наш Чат, в котором вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.
Помощь проекту:
В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади шара/сферы
- 1. Через радиус
- 2. Через диаметр
- Примеры задач
Формула вычисления площади шара/сферы
1. Через радиус
Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.
S = 4 π R2
Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:
S = 4 π (d/2)2
Примеры задач
Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.
Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)2 = 615,44 см2.
Задание 2
Площадь поверхности сферы равна 200,96 см2. Найдите ее диаметр.
Решение:
Выведем величину диаметра из соответствующей формулы расчета площади: