Как найти площадь сечения треугольной трапеции

Имеется верное доказательство утверждения пункта а)

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Источник

Площадь сечения правильной треугольной призмы трапеция

В правильной треугольной призме ABCA’B’C’ стороны основания равны 6, а боковые ребра равны 4. Изобразите сечение, проходящее через вершины A, B и середину ребра A’C’. Найдите его площадь

Параллельные грани оснований сечение пересекает по параллельным прямым, поэтому сечение — трапеция. Пусть точка М — середина A’C’, точка N — середина B’С’. Боковые стороны трапеции ABNM являются гипотенузами равных прямоугольных треугольников AA’M и BB’N, катеты которых равны 3 и 4. Тем самым, трапеция является равнобедренной, а ее боковые стороны равны 5.

Отрезок MN — средняя линия треугольника A’B’C’, поэтому MN = 0,5A’C’ = 3. Пусть MH — высота трапеции, тогда

Критерии оценивания выполнения задания Баллы
Обоснованно получен верный ответ 2
Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено; а также, если при правильном ответе решение недостаточно обосновано 1
Решение не соответствует ни одному из критериев, перечисленных выше 0
Максимальный балл 2

Аналоги к заданию № 500962: 500968 501124 Все

Источник

Особенности трапециевидной призмы и способ расчета объема

трапециевидная призма это призма такая, что задействованные полигоны являются трапециевидными. Определение призмы — это такое геометрическое тело, которое образовано двумя равными и параллельными друг другу многоугольниками, а остальные их грани являются параллелограммами..

Призма может иметь разные формы, которые зависят не только от количества сторон многоугольника, но и от самого многоугольника..

Если многоугольники, входящие в состав призмы, являются квадратами, то это отличается от призмы, которая включает в себя, например, бриллианты, даже если оба многоугольника имеют одинаковое количество сторон. Таким образом, это зависит от того, какой четырехугольник участвует.

Характеристики трапециевидной призмы

Чтобы увидеть характеристики трапециевидной призмы, вы должны сначала узнать, как она нарисована, затем, каким свойствам соответствует основание, какова площадь поверхности и, наконец, как рассчитывается ее объем..

1- Рисование трапециевидной призмы

Чтобы нарисовать его, нужно сначала определить, что такое трапеция.

Трапеция представляет собой неправильный многоугольник с четырьмя сторонами (четырехугольник), так что у него есть только две параллельные стороны, называемые основаниями, а расстояние между его основаниями называется высотой.

Чтобы нарисовать прямую трапециевидную призму, начните с рисования трапеции. Затем вертикальная линия длиной «h» проецируется из каждой вершины и, наконец, рисуется другая трапеция, так что ее вершины совпадают с концами ранее нарисованных линий..

Вы также можете иметь наклонную трапециевидную призму, конструкция которой аналогична предыдущей, вам просто нужно нарисовать четыре линии, параллельные друг другу..

2- Свойства трапеции

Как было сказано ранее, форма призмы зависит от многоугольника. В частном случае трапеции мы можем найти три различных типа основ:

-Трапециевидный прямоугольник: является ли эта трапеция такой, что одна из ее сторон перпендикулярна ее параллельным сторонам или что она просто имеет прямой угол.

-Равнобедренная трапеция: трапеция такая, что ее непараллельные стороны имеют одинаковую длину.

Шкала трапеции: это та трапеция, которая не равнобедренная или прямоугольная; его четыре стороны имеют разную длину.

Как вы можете видеть в соответствии с типом трапеции, будет получена другая призма.

3- Площадь поверхности

Чтобы вычислить площадь поверхности трапециевидной призмы, нам нужно знать площадь трапеции и площадь каждого параллелограмма..

Как вы можете видеть на предыдущем изображении, область включает в себя две трапеции и четыре разных параллелограмма..

Площадь трапеции определяется как T = (b1 + b2) xa / 2, а площади параллелограммов: P1 = hxb1, P2 = hxb2, P3 = hxd1 и P4 = hxd2, где «b1» и «b2» основания трапеции, «d1» и «d2» непараллельные стороны, «a» — высота трапеции, а «h» — высота призмы..

Следовательно, площадь поверхности трапециевидной призмы A = 2T + P1 + P2 + P3 + P4.

4- Том

Поскольку объем призмы определяется как V = (площадь многоугольника) x (высота), можно сделать вывод, что объем трапециевидной призмы равен V = Txh..

5- Приложения

Одним из наиболее распространенных объектов, имеющих форму трапециевидной призмы, является золотой слиток или пандусы, используемые в гонках на мотоциклах..

Источник

Нахождение площади правильной призмы: формула и задачи

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.

Формула площади правильной призмы

1. Общая формула

Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.

Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.

Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.

2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

3. Площадь правильной четырехугольной призмы

Основание: квадрат.

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Площадь Формула
основание
боковая поверхность
полная

Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a 2 . А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a 2 .

4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Источник

Площадь трапеции через основания и высоту

{S = dfrac{1}{2} (a + b) cdot h}

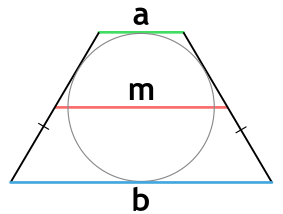
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций — обычная, равнобедренная (равнобокая).

  1. Калькулятор площади трапеции
  2. Площадь трапеции
    1. через основания и высоту
    2. через среднюю линию и высоту
    3. через диагонали и среднюю линию
    4. через 4 стороны
    5. через диагонали и угол между ними
    6. через основания и углы при основании
    7. через площади треугольников
    8. через диагонали и высоту
    9. через радиус вписанной окружности и основания
    10. через перпендикулярные диагонали
  3. Площадь равнобедренной (равнобокой) трапеции
    1. через основания и высоту
    2. через 3 стороны (формула Брахмагупты)
    3. через верхнее основание, боковую сторону и угол при нижнем основании
    4. через нижнее основание, боковую сторону и угол при нижнем основании
    5. через основания и угол
    6. через диагонали и угол между ними
    7. через боковую сторону, угол при основании и среднюю линию
    8. через радиус вписанной окружности и угол при основании
  4. Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
    1. через высоту (диаметр вписанной окружности) и угол при основании
    2. через основания и угол при основании
    3. через основания и радиус вписанной окружности
    4. через основания
    5. через основания и боковую сторону
    6. через основания и среднюю линию
  5. Примеры задач

Площадь трапеции

Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

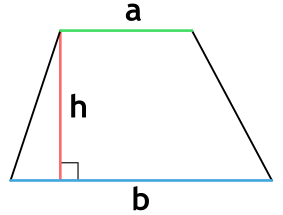
Площадь трапеции через основания и высоту

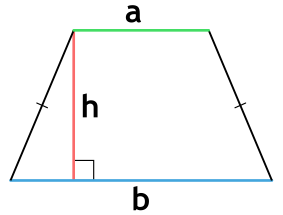
Площадь трапеции через основания и высоту

{S = dfrac{1}{2} (a + b) cdot h}

a и b — основания трапеции

h — высота, проведенная к основанию

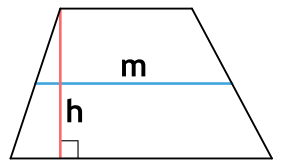
Площадь трапеции через среднюю линию и высоту

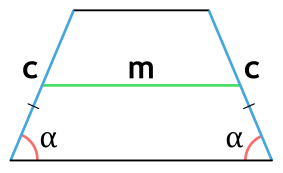
Площадь трапеции через среднюю линию и высоту

{S = m cdot h}

m — средняя линия трапеции

h — высота трапеции

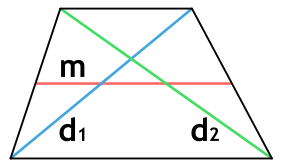
Площадь трапеции через диагонали и среднюю линию

Площадь трапеции через диагонали и среднюю линию

{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}

d1 и d2 — диагонали трапеции

m — средняя линия трапеции

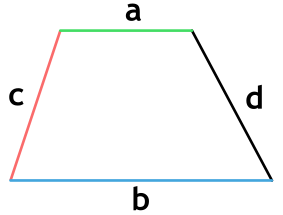
Площадь трапеции через 4 стороны

Площадь трапеции через 4 стороны

{S = dfrac{a+b}{2} sqrt{c^2 — {Big( dfrac{(a-b)^2 + c^2 — d^2}{2(a-b)} Big)}^2}}

a, b, c и d — стороны трапеции

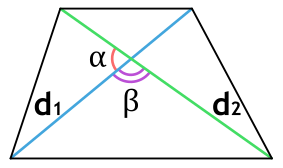
Площадь трапеции через диагонали и угол между ними

Площадь трапеции через диагонали и угол между ними

{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}

d1 и d2 — диагонали трапеции

α или β — угол между диагоналями трапеции

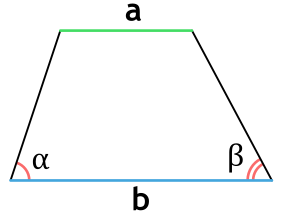
Площадь трапеции через основания и углы при основании

Площадь трапеции через основания и углы при основании

{S = dfrac{b^2 — a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}

a и b — основания трапеции

α или β — прилежащие к основанию трапеции углы

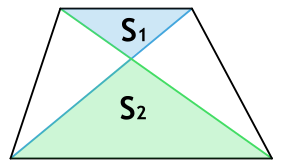
Площадь трапеции через площади треугольников

Площадь трапеции через площади треугольников

{S = (sqrt{S_1} + sqrt{S_2})^2}

S1 и S2 — площади образованных пересечением диагоналей трапеции треугольников

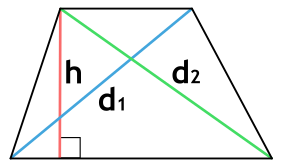
Площадь трапеции через диагонали и высоту

Площадь трапеции через диагонали и высоту

{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}

d1 и d2 — диагонали трапеции

h — высота трапеции

Площадь трапеции через радиус вписанной окружности и основания

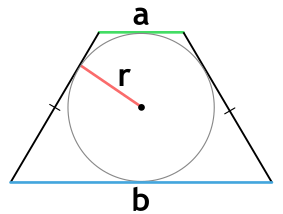
Площадь трапеции через радиус вписанной окружности и основания

{S = (a+b)cdot r}

a и b — основания трапеции

r — радиус вписанной в трапецию окружности

Площадь трапеции через перпендикулярные диагонали

Площадь трапеции через перпендикулярные диагонали

{S = dfrac{1}{2} cdot d_1 cdot d_2}

d1 и d2 — перпендикулярные диагонали трапеции

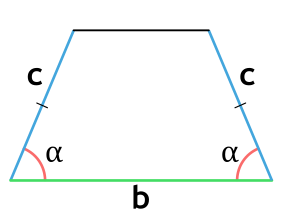
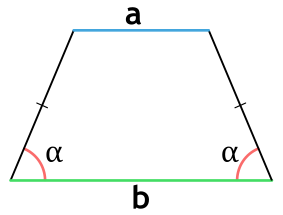
Площадь равнобедренной (равнобокой) трапеции

Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.

Площадь равнобедренной трапеции через основания и высоту

Площадь равнобедренной трапеции через основания и высоту

{S = dfrac{a+b}{2} cdot h}

a и b — основания равнобедренной трапеции

h — высота, проведенная к основанию равнобедренной трапеции

Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

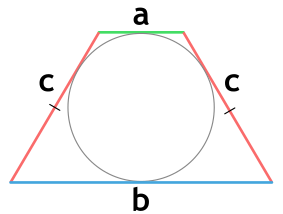
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}

a и b — основания равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}

a — верхнее основание равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

α — прилежащие к нижнему основанию трапеции углы

Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании

Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}

b — нижнее основание равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

α — прилежащий к нижнему основанию трапеции угол

Площадь равнобедренной трапеции через основания и угол

Площадь равнобедренной трапеции через основания и угол

{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}

a и b — основания равнобедренной трапеции

α — прилежащий к основанию трапеции угол

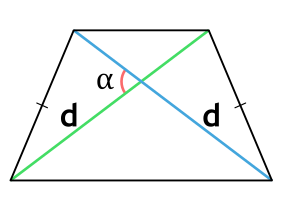
Площадь равнобедренной трапеции через диагонали и угол между ними

Площадь равнобедренной трапеции через диагонали и угол между ними

{S = dfrac{1}{2}d^2 cdot sin(alpha)}

a — диагональ равнобедренной трапеции

α — угол между диагоналями равнобедренной трапеции

Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию

Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию

{S = m cdot c cdot sin(alpha)}

m — средняя линия равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

α — угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

{S = dfrac{4r^2}{sin(alpha)}}

r — радиус вписанной окружности

α — угол при основании равнобедренной трапеции

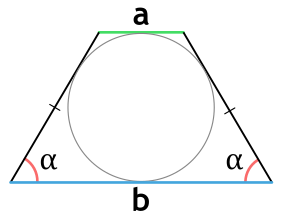
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность

В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.

Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

{S = dfrac{h^2}{sin(alpha)}}

h — высота равнобедренной трапеции

α — угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании

{S = dfrac{a cdot b}{sin(alpha)}}

a и b — основания равнобедренной трапеции

α — угол при основании равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности

{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}

a и b — основания равнобедренной трапеции

r — радиус вписанной окружности

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}

a и b — основания равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону

{S = c cdot sqrt{a cdot b}}

a и b — основания равнобедренной трапеции

c — боковая сторона равнобедренной трапеции

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию

Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию

{S = m cdot sqrt{a cdot b}}

a и b — основания равнобедренной трапеции

m — средняя линия равнобедренной трапеции

Примеры задач на нахождение площади трапеции

Задача 1

Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.

Решение

Для решения задачи воспользуемся первой формулой.

S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2

Ответ: 37.5 см²

Полученный ответ легко проверить с помощью калькулятора .

Задача 2

Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.

Решение

С решением этой задачи нам поможет вторая формула.

S = m cdot h = 18 cdot 9 = 162 : см^2

Ответ: 162 см²

Воспользуемся калькулятором для проверки результата.

Задача 3

Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.

Решение

Для решения этой задачи нам поможет третья формула.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2

Ответ: 24 см²

Осталось проверить полученный ответ.

Задача 4

Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.

Решение

Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2

Ответ: 60 см²

Проверка .

Задача 5

Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.

Решение

Еще одна типовая задача. Повторим действия как в задачах выше.

На первом этапе вычислим p:

p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2

Ответ: 24 см²

Проверка .

Задача 6

Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.

Решение

Для решения этой задачи используем формулу Брахмагупты.

Сначала вычислим p:

p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21

А теперь можно вычислить площадь трапеции:

S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2

Ответ: 88 см²

Проверка .

Задача 7

Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.

Решение

Для решения этой задачи воспользуемся формулой.

S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)

Тангенс 45° = 1, продолжим вычисления:

S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2

Ответ: 14 см²

Убедиться в правильности решения нам поможет калькулятор .

Источник

Выбирайте формулу в зависимости от известных величин.

1. Как найти площадь трапеции через основания и высоту

Посчитайте сумму оснований трапеции.

Умножьте результат на высоту и поделите на два.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • a и b – основания трапеции (её параллельные стороны).
  • h – высота трапеции.

2. Как вычислить площадь трапеции через высоту и среднюю линию

Просто умножьте высоту трапеции на среднюю линию.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
  • h – высота трапеции.

3. Как найти площадь трапеции через диагонали и угол между ними

Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.

Поделите результат на два.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • x и y – диагонали трапеции.
  • α – любой угол между диагоналями.

4. Как найти площадь трапеции через четыре стороны

Отнимите от большего основания меньшее.

Найдите квадрат полученного числа.

Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.

Поделите полученное число на удвоенную разность оснований.

Найдите квадрат результата и отнимите его от квадрата боковой стороны.

Найдите корень из полученного числа.

Умножьте результат на половину от суммы оснований.

Иллюстрация: Лайфхакер
  • S – искомая площадь трапеции.
  • a, b – основания трапеции.
  • c, d – боковые стороны.

5. Как вычислить площадь равнобедренной трапеции через четыре стороны

Отнимите от большего основания трапеции меньшее и поделите результат на два.

Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.

Найдите корень из результата.

Умножьте полученное число на сумму оснований и поделите на два.

Иллюстрация: Лайфхакер
  • S — искомая площадь трапеции.
  • a, b — основания трапеции.
  • c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).

6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол

Найдите квадрат радиуса и умножьте его на четыре.

Поделите результат на синус известного угла.

Иллюстрация: Лайфхакер
  • r — радиус вписанной окружности.
  • α — любой угол трапеции.

Читайте также 📐✏️🎓

  • 8 способов найти длину окружности
  • 8 способов найти периметр треугольника
  • 7 способов найти площадь прямоугольника
  • Как перевести обычную дробь в десятичную
  • Как освоить устный счёт школьникам и взрослым
Источник

Тема 13.

Задачи по стереометрии

13

.

12

Нахождение площади сечения

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

задачи по стереометрии

Решаем задачи

Показать ответ и решение

Ответ:

б) √ -- 19-70 7

Показать ответ и решение

Ответ:

7a2√34 ------- 36

Показать ответ и решение

а) Обозначим через α плоскость сечения. Плоскости (B1C1D1 ) и (BCD )
параллельны, следовательно, плоскость α сечет их по параллельным прямым.
Плоскость α пересекает B1C1D1 по прямой D1C1. Докажем, что прямая EB
параллельна D1C1, из этого будет следовать, что она лежит в α, так как
B ∈ α .

Прямые EB ∥ DC в силу правильности шестиугольника ABCDEF, так как в
нем ∘ ∠BED = 60, ∘ ∠EDC = 120 , следовательно, сумма односторонних углов
равна 180∘. Прямые DC ∥D C , 1 1 следовательно, EB ∥ D C . 1 1 Тогда E лежит в
α и ED1C1B — искомое сечение. Кроме того, в четырехугольнике ED1C1B
противолежащие стороны EB и D1C1 параллельны и не равны, следовательно,
ED1C1B — трапеция.

PIC

б) Способ 1.

В правильном шестиугольнике EB = 2DC = 2AB = 20, также по условию
D1C1 = AB = 10. По теореме Пифагора для треугольника BCC1 :

BC = ∘BC2-+-CC2-= √100-+100-=10√2-= ED 1 1 1

Найдем полупериметр трапеции:

√ - √- p= 2⋅10-2+-10+-20= 15+ 10 2 2

Равнобокую трапецию можно вписать в окружность, тогда по формуле
Брахмагупты ее площадь равна

S = ∘ (p−-ED1)(p−-D1C1)(p-− BC1-)(p-− EB-)=

∘ -2-------√---------√--- √- = 15 ⋅(5+ 10 2)(−5+ 10 2)= 75 7

Способ 2.

Введём векторный базис из векторов −A→F =−→a, −B−→C = −→b , −−C→C1 = −→c. Длины
этих векторов a =b = c= 10. Из определения правильной призмы −→a ⊥ −→c
и −→ −→ b ⊥ c , а поскольку шестиугольник ABCDEF — правильный, то
прямые AF и BC образуют угол ∘ 60. Тогда можно посчитать скалярное
произведение:

(−→a,−→b )= a⋅b⋅cos60∘ = 10⋅10⋅0,5 = 50 −→ −→ ∘ (a, c)= a⋅c⋅cos90 = 0 (−→b ,−→c)= b⋅c⋅cos90∘ = 0

PIC

В пункте а) было ранее доказано, что EBC1D1 — трапеция. По свойствам
правильного шестиугольника диагональ BE = 2a. Тогда для определения
площади сечения можно сначала посчитать площадь треугольника EBC1, после
чего домножить её на 1,5, поскольку площадь EC1D1 составляет половину от
площади EBC1. Выразим векторы BE и BC1 через базисные вектора и найдём
квадраты длин:

−−→ −→ BE =2AF =2−→a −−→ −−→ −−→ −→ −→ BC1 = BC + CC1 = b + c BE2 = (2a)2 = 4a2 = 202 −→ −→ 2 −→ −→ 2 −→ −→ 2 −→ −→ 2 2 2 2 BC1 = (b , c) = (b , b ) +( c,c) − 2(b , c)= b + c = 2a =2 ⋅10

Таким образом,

1 1 ∘------------- SEBC1 = 2BE ⋅BC1 sin ∠EBC1 = 2BEBC1 1 − cos2∠EBC1 = ∘ --------------------------- ∘------------------- = 1 BE2BC21 − BE2BC21 cos2∠EBC1 = 1 BE2BC21 − (−B−→E, −B−C→1)2 = 2 ∘ ----------------- ∘ ---2------------------ = 1 8a4− (2−→a,−→b + −→c )2 = 1 8a4 − 4(−→a ,−→b )2− 4(−→a,−→c)2 = 2 ∘ ---------------2-- = 1 2⋅2002− 4⋅502− 2⋅0= 1 ⋅100√8-−-1= 50√7 2 2

Тогда площадь трапеции равна

√- SEBC1D1 = 1,5SEBC1 = 75 7

Ответ:

б) √ - 75 7

Критерии оценки

Содержание критерия

Балл

Имеется верное доказательство
утверждения пункта а) и обоснованно
получен верный ответ в пункте б)

3

Обоснованно получен верный ответ в
пункте б)

2

ИЛИ

имеется верное
доказательство утверждения пункта
а) и при обоснованном решении
пункта б) получен неверный ответ
из-за арифметической ошибки

Имеется верное доказательство
утверждения пункта а)

1

ИЛИ

при обоснованном решении пункта
б) получен неверный ответ из-за
арифметической ошибки

ИЛИ

обоснованно получен верный ответ в
пункте б) с
использованием утверждения пункта
а), при этом пункт а) не выполнен

Решение не соответствует ни одному
из критериев, перечисленных выше

0

Максимальный балл

3

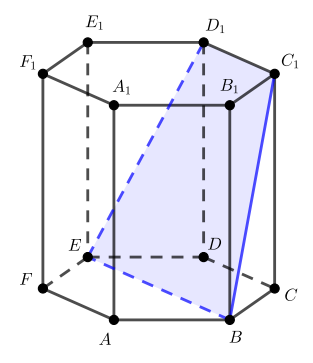
Правильная треугольная пирамида рассечена плоскостью, перпендикулярной основанию и делящей две стороны
основания пополам. Найдите площадь сечения пирамиды этой плоскостью, если известно, что сторона основания равна
2 , а высота пирамиды равна 4 .

Показать ответ и решение

Ответ:

1,5

Показать ответ и решение

1) Пусть AC ∩ BD = O . Две плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

 PIC

 Заметим, что т.к. ∠SAB = ∠SAD = 90 ∘ ⇒ SA ⊥ (ABC ) .

Проведем в плоскости SAC прямую OK ∥ SC . Т.к. O – середина AC , то по теореме Фалеса K
– середина SA . Через точку K в плоскости SAB проведем KM ∥ SB (следовательно, M –
середина AB ). Таким образом, плоскость, проходящая через прямые OK и KM , и будет искомой
плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M , получим прямую
M N .

Т.к. α ∥ (SBC ) ,то α пересечет плоскость SCD по прямой N P ∥ SC (если N P ∩ SC ⁄= ∅ , то
α ∩ (SBC ) ⁄= ∅ , что невозможно ввиду их параллельности).

Таким образом, KM N P – искомое сечение, причем KP ∥ AD ∥ M N ⇒ это трапеция.

2) Т.к. все точки K, M, N, P – середины отрезков SA, AB, CD, SD соответственно,
то:

а) M N = AD = a

б) KP = 1-AD = a- 2 2

в) √ -- KM = 1SB = a--2- 2 2

Заметим, что по теореме о трех перпендикулярах SB ⊥ BC ⇒ KM ⊥ M N . Таким образом,
KM N P – прямоугольная трапеция.

√ -- KP---+-M-N-- 3--2-2 SKMNP = 2 ⋅ KM = 8 a

Ответ:

1) Рисунок.

2) √ -- 3 2 2 ----a 8

Показать ответ и решение

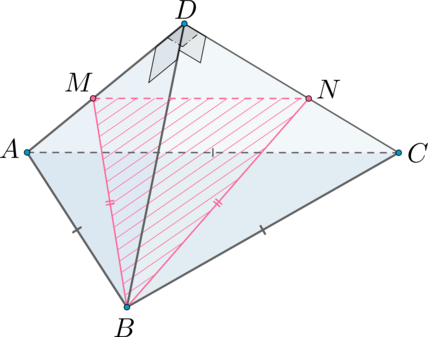
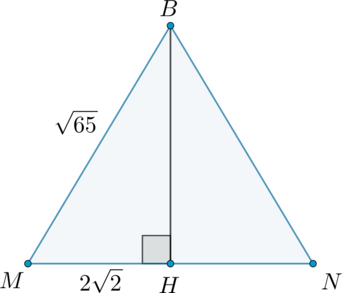
б) По теореме Менелая для △ADC и прямой QK имеем:

AN-- ⋅ DK- ⋅ CQ-= 1 ⇒ QA = 8 N D KC QA

По условию AM = 13AB = 8 . Т.к. QA = AM и ∠CAB = 60∘ ⇒ ∠AQM = 30∘ . Следовательно,
∠BM T = 30∘ , тогда ∠M T B = 90∘ . Следовательно, BT = 8 . Заметим, что △N DK = △M BT по
углу и двум прилежащим сторонам, следовательно, M T = N K . Также заметим, что так как
BT = DK = 8 , то TK ∥ DB . Также и M N ∥ DB . Следовательно, M N KT – равнобедренная
трапеция.

Основания M N = 8 , KT = 16 , по теореме Пифагора √ -------- √ -- M T = 162 − 82 = 8 3 . Следовательно,
если провести высоту M H , то T H = 0,5(16 − 8) = 4 . Тогда по теореме Пифагора
∘ --√--------- √ --- M H = (8 3)2 − 42 = 4 11 . Следовательно,

8-+-16- √ --- √ --- SMNKT = 2 ⋅ 4 11 = 48 11

Ответ:

б) √ --- 48 11

Показать ответ и решение

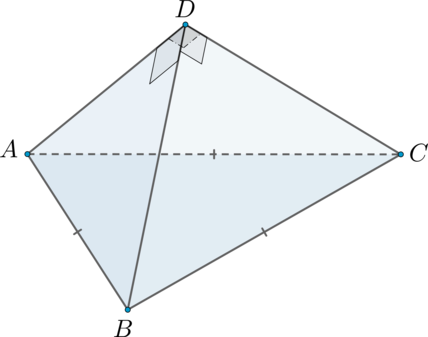
а) Для того, чтобы доказать, что пирамида является правильной, нужно доказать, что в основании
пирамиды находится правильный многоугольник, а боковые ребра равны.
PIC
Возьмем за основание △ABC – он правильный по условию.
Осталось доказать, что DA = DC = DB .
Рассмотрим △ADB и △CDB . Они прямоугольные и равны по катету и гипотенузе. Следовательно,
DA = DC . Аналогично рассматривая другие боковые грани, доказываем, что DA = DB .
Следовательно, DA = DB = DC , чтд.

б) Заметим, что так как DM : M A = DN : N C = 4 : 3 и боковые грани – равные треугольники, то
BM = BN . PIC
Так как DM : M A = DN : N C = 4 : 3 , то по теореме Фалеса M N ∥ AC , также △DM N ∼ △DAC .
Из подобия следует:

M N DM 4 4 √ -- -----= -----= -- → M N = -AC = 4 2 AC DA 7 7

Найдем BM .
Так как △ADB прямоугольный и равнобедренный, то √ -- DA = DB = AB : 2 , следовательно,
DA = 7 .
Рассмотрим прямоугольный △DM B . Так как 4 DM = 7DA = 4 , то √ -2---2- √ --- BM = 4 + 7 = 65 .
Рассмотрим теперь △BM N : PIC
Так как он равнобедренный, то высота BH , проведенная к основанию, будет также и медианой.
Следовательно,

√ ------- √ --- BH = 65 − 8 = 57

Таким образом,

1 √ ---- S△BMN = --⋅ BH ⋅ M N = 2 114 2

Ответ:

б) √ ---- 2 114

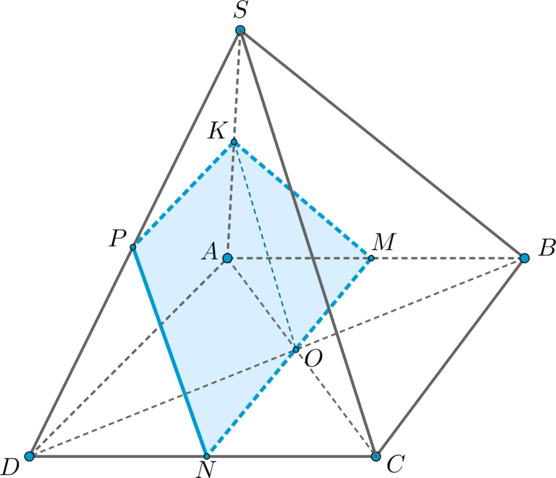
Дана правильная четырехугольная пирамида SABCD с вершиной S , стороны основания которой
равны √ -- 6 2 , а боковые ребра равны 21 .

а) Постройте сечение пирамиды плоскостью, проходящей через точку A и середину ребра SC
параллельно прямой BD .

б) Найдите площадь построенного сечения.

Показать ответ и решение

б) Заметим, что по теореме о трех перпендикулярах (так как OH ⊥ (ABC ),AH ⊥ BD )
AO ⊥ BD . Так как BD ∥ M K , то AO ⊥ M K , следовательно, AN ⊥ M K . Следовательно, у
четырехугольника AM N K диагонали взаимно перпендикулярны. Значит, его площадь можно найти
как

S = 1AN ⋅ M K. 2

Заметим сразу, что √ -- BD = AC = AB 2 = 12 .
Рассмотрим плоскость ASC .

 PIC

 По теореме Менелая:

-SN- ⋅-CA- ⋅ HO- = 1 ⇒ HO--= 1- ⇒ OS = 2OH ⇒ SO--= 2. N C AH OS OS 2 SH 3

(это
нам понадобится позже для поиска M K )

 Проведем N Q ⊥ AC . Тогда из подобия △SHC и △N QC :

√ ------------ √-------- √ ------ SH-- = SC--= 2 ⇒ N Q = 1SH = 1- SC2 − HC2 = 1- 212 − 62 = 1- 81 ⋅ 5 N Q N C 2 2 2 2

Q –
середина HC , следовательно, 3 3 AQ = 4AC = 4 ⋅ 12 = 9 . Тогда по теореме Пифагора

∘ ------------ ∘ ----------- AN = AQ2 + N Q2 = 81-⋅ 5-+ 81 = 27-. 4 2

Рассмотрим BSD . Так как △M SK ∼ △BSD , то

M K SO 2 2 2 -----= ----= -- ⇒ M K = -BD = --⋅ 12 = 8. BD SH 3 3 3

Следовательно, площадь сечения равна

S = 1-⋅ 8 ⋅ 27-= 54. 2 2

Показать ответ и решение

1) ПустьK – середина AC , SX, AL – медианы грани ASB , CL, SY – медианы грани CSB ,
AL ∩ SX = M, CL ∩ SY = N . SO – высота пирамиды.

Найдем сечение пирамиды плоскостью M N K .
Т.к. пирамида правильная, то △SXY – равнобедренный, 2 SM = SN = -SX ⇒ M N ∥ XY ⇒ M N ∥ (ABC ) 3 .
Таким образом, плоскость M N K содержит прямую M N , параллельную ABC , следовательно,
плоскость M N K пересечет плоскость ABC по прямой, параллельной M N (если это не так, то линия
пересечения этих плоскостей l ∩ M N = E ⇒ E ∈ (ABC ) и E ∈ M N ⇒ M N не может быть
параллельна (ABC ) ).

PIC

Прямая, проходящая через точку K и параллельная M N (или XY ) – это AC . Следовательно,
сечением является равнобедренный треугольник ALC .

2) Пусть LK ∩ SO = H . Тогда по теореме о трех перпендикулярах HK ⊥ AC как наклонная
(HO ⊥ (ABC ),OK ⊥ AC как проекция). Следовательно, и LK ⊥ AC .

Тогда 1- SALC = 2AC ⋅ LK .

PIC

Рассмотрим √ -- √ -- √ -- △SKB : BK = AB ⋅--3-= 21--3-⇒ cosB = -7√-3- 2 2 12 2 .

Тогда по теореме косинусов для △KLB :

2 729- 27- KL = 4 ⇒ KL = 2

Значит, SALC = 567- 4 .

Ответ:

567 ---- 4 .

Показать ответ и решение

а) 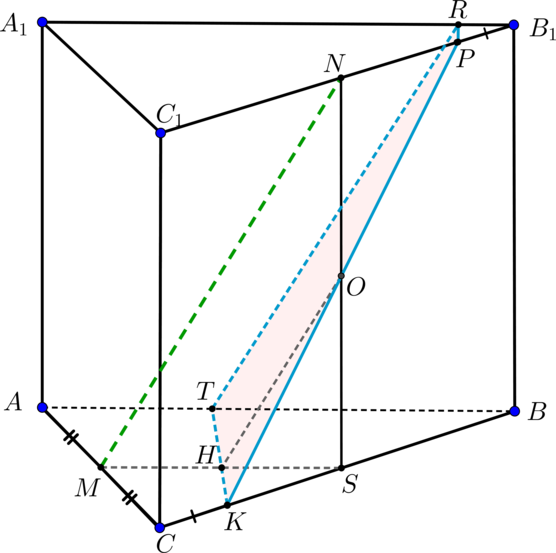PIC

Если прямая M N ∥ α ⇒ M N параллельна некоторой прямой, лежащей в α . Проведем
N S ⊥ BC, N S ∩ KP = O . В плоскости M N S проведем OH ∥ M N ⇒ M H = HS . Тогда прямая
KH ∩ AB = T . Так как плоскости ABC и A1B1C1 параллельны, то α пересечет плоскость A1B1C1
по прямой, параллельной KT . Следовательно, проведем P R ∥ KT . Таким образом, TRP K – искомое
сечение (трапеция).

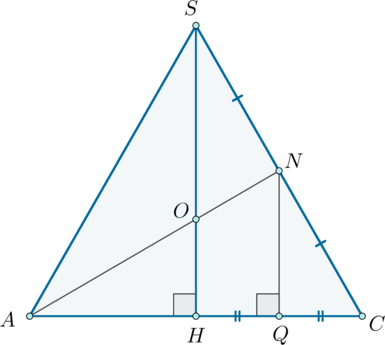
б) Заметим, что 1 5 CK = --⋅ 15 =--⇒ KS = 5 6 2 . Т.к. M S – средняя линия треугольника
ABC ⇒ M S = 8 ⇒ HS = 4 . Так как ∠HSK = ∠ABC , то по теореме косинусов
∘ -------------------- HK = 16 + 25 − 2 ⋅ 4 ⋅ 5 ⋅ 45 = 3 . Таким образом, по обратной теореме Пифагора треугольник HKS –
прямоугольный, следовательно, ∠H = 90 ∘ . Таким образом, по теореме о трех перпендикулярах, из
того, что N S ⊥ (ABC ),HS ⊥ KT ⇒ OH ⊥ KT .

Найдем основания трапеции KT и P R .

sin ∠KSH = 3-= sin ∠B = KT-- ⇒ KT = 15- 5 KB 2 .

3 △ PRB1 ∼ △KT B ⇒ P R = -- 2 .

Таким образом, ( ) 1- 15- 3- √ -- √ -- STRP K = 2 ⋅ 2 + 2 ⋅ 8 2 = 36 2

Ответ:

б) √ -- 36 2

Показать ответ и решение

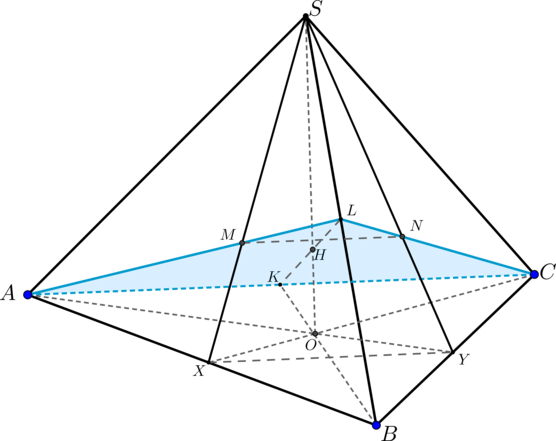
а) 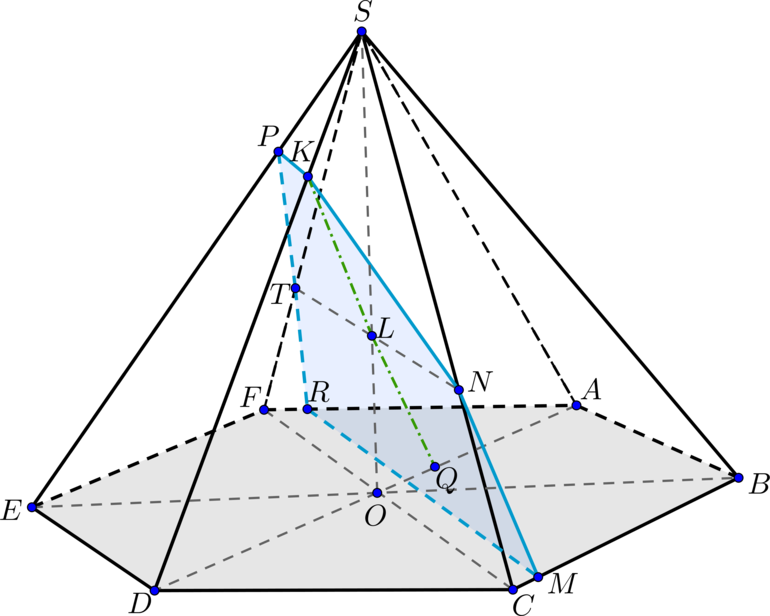PIC

Две плоскости параллельны, если две пересекающиеся прямые из одной плоскости будут
параллельны некоторых двум пересекающимся прямым из другой плоскости.Проведем через точку L
прямые, параллельные AB и AS .
Из свойства правильного шестиугольника следует, что F C ∥ AB . Проведем в плоскости F SC через
точку L : T N ∥ F C .

Тогда по теореме Фалеса SN ST SL 3 ----= ----= ----= -- N C TF LO 1

В плоскости ASD проведем через точку L : KQ ∥ SA .

Из теоремы Фалеса следует, что AQ SL 3 ----= ----= -- QO LO 1

Пусть AQ = 3x,QO = x . Из свойств правильного шестиугольника следует, что DO = OA = 4x .

Тогда по теореме Фалеса DQ--= DK-- = 5x-= 5- QA KS 3x 3

б) Достроим сечение пирамиды плоскостью α . Плоскость α пересечет плоскость основания по
прямой RM ∥ AB, Q ∈ RM . Значит, BM--- AR-- 3- M C = RF = 1

Найдем все их стороны.
Из подобия 3 3 △ ST N ∼ △SF C ⇒ TN = -F C = -a = 6 4 2
Из подобия △ CN M ∼ △CSB ⇒ N M = 1-b = 7- 4 4

Достроим трапецию F ABC до треугольника F W C – он правильный. 7 7 ⇒ RM = -F C = -a = 7 8 4
Из подобия 3 3 3 △ SP K ∼ △SED ⇒ P K = -ED = --a = -- 8 8 2

Найдем KN из грани SCD :
По теореме косинусов 2b2 − a2 cos∠S = -----2-- 2b .

В △ KSN : 3- 3- KN = 8b,SN = 4b ⇒ по теореме косинусов 2 -9- 2 2 27- KN = 64 ⋅ (b + 2a ) ⇒ KN = 8

Обозначим высоту трапеции M N T R за h1 . Тогда ∘ -------- 49- 1- 3-√ -- h1 = 16 − 4 = 4 5

Высота трапеции N KP T h = ∘ -272−--81-= 9√5-- 1 64 16 8

Тогда площадь сечения ( ) √-- √-- √ -- S = 1-⋅ 3-+ 6 ⋅ 9 5 + 1⋅ (6 + 7) ⋅ 3 5 = 291--5- 2 2 8 2 4 32

Ответ:

б) √-- 291--5- 32

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

1

2

3

4

5

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти силу тока протекающего через лампу
  • Как найти высоту треугольника зная его основание
  • Как найти добросовестного работодателя
  • Как найти на кого зарегистрирована симка
  • Маржинальный доход как его найти формула

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии