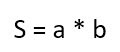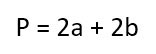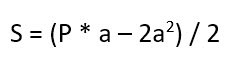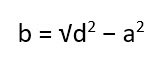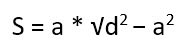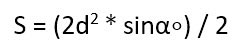- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
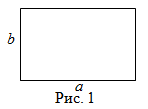
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней — 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
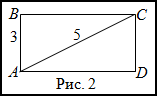
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ — 5 м.
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела «Как найти площадь»

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Выбирайте формулу, ориентируясь на известные величины.
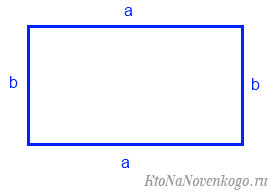
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Загрузить PDF
Загрузить PDF
Прямоугольник — четырехсторонняя фигура с четырьмя прямыми углами, противолежащие стороны которой равны. Все, что нужно сделать для вычисления его площади, — умножить длину на ширину. Хотите знать как это сделать? Читайте дальше.
-
1
Прямоугольник — четырехсторонняя фигура, противолежащие стороны которой равны. Если одна сторона равна 10 см, то и противолежащая будет равна 10 см.
- Любой квадрат также является прямоугольником. Площадь квадрата находится по той же формуле.
-
2
Выучите формулу нахождения площади прямоугольника: S = a * b, где S — площадь, a — длина, b — ширина, то есть, площадь равна произведению сторон.
Реклама
-
1
Найдите длину прямоугольника. Как правило, она указана в задаче, но если нет — найдите ее с помощью линейки.
- Двойные отметки на длинных сторонах означают, что их длины равны.
-
2
Так же найдите ширину прямоугольника.
- Отметки на узких сторонах означают, что их ширины равны.
-
3
Запишите длину и ширину. В нашем примере длина — 5 см, ширина — 4 см.
-
4
Умножьте длину на ширину. Длина — 5 см, ширина — 4 см, вставьте эти числа в формулу S = a * b и вы найдете площадь.
- S = 4 cm * 5 cм
- S = 20 cм^2
-
5
Запишите ответ в квадратных единицах. Ответ: 20 см^2, что означает «двадцать квадратных сантиметров».
- Ответ можно записать как 20 кв. см, так и 20 см^2.
Реклама
-
1
Научитесь использовать теорему Пифагора — она позволяет найти длину стороны прямоугольного треугольника, если известны длины двух других сторон. Можно использовать ее для нахождения гипотенузы, самой длинной из сторон треугольника, а также длины и ширины, образующих прямой угол.
- Прямоугольник имеет четыре прямых угла, и его диагональ образует два прямоугольных треугольника, так что мы можем использовать теорему Пифагора.
- Теорема Пифагора звучит так: квадрат гипотенузы равен сумме квадратов катетов, то есть a^2 + b^2 = c^2, где a и b — стороны (катеты) прямоугольного треугольника, а с — гипотенуза, самая длинная сторона.
-
2
Используйте теорему Пифагора для нахождения другой стороны треугольника. К примеру, прямоугольник имеет сторону длиной 6 см и диагональ длиной 10 см. Одна сторона — 6 см, другая — b, гипотенуза — 10 см. Вставьте значения в теорему и решите. Вот, как это делается:
- Пример: 6^2 + b^2 = 10^2
- 36 + b^2 = 100
- b^2 = 100 — 36
- b^2 = 64
- квадратный корень (b) = квадратный корень (64)
- b = 8
- Длина другой стороны треугольника, которая также является другой стороной прямоугольника, — 8 см.
-
3
Найдите площадь прямоугольника. Поскольку для нахождения длины и ширины мы использовали теорему Пифагора, все, что нам нужно, — это помножить длину на ширину:
- Пример: 6 cм * 8 cм = 48 cм^2
-
4
Запишите окончательный ответ в квадратных единицах: 48 cм^2 или 48 кв. см.
Реклама
Советы
- Все квадраты — прямоугольники, но не все прямоугольники — квадраты.
- При нахождении площади ответ всегда нужно записывать в квадратных единицах.
Реклама
Об этой статье
Эту страницу просматривали 279 895 раз.
Была ли эта статья полезной?
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Площадь прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем, как вычислять площадь прямоугольника.
Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.
Что такое площадь прямоугольника
Но для начала давайте все-таки дадим основные определения:
Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.
Прямоугольник является параллелограммом (что это такое?) и выглядит вот так:
А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.
Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.
В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.
Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».
Для площади геометрических фигур действуют определенные правила:
- Она не может быть отрицательной.
- У равных фигур всегда равные площади.
- Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
- Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.
Обычно фигуры, которые имеют равные площади, называют «равновеликими».
Как найти площадь прямоугольника
Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.
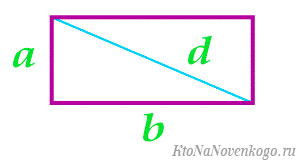
Возьмем, к примеру, такой прямоугольник:
Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:
Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.
Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.
Формула площади прямоугольника через периметр
Если известна длина только одной стороны, но известен еще и периметр прямоугольника.
В этом случае есть два варианта.
- Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:
И тогда обратные расчеты выглядят вот так:
Ну а после того, как станет известна длина второй стороны прямоугольника, можно прибегнуть к классической формуле.
- Ну и второй вариант – воспользоваться сразу готовой формулой:
Площадь прямоугольника через диагональ
-
Известна одна сторона и длина диагонали.
Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.
Второй вариант – опять же сразу прибегнуть к готовой формуле:
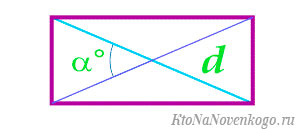
-
Если известны длина диагоналей и угол между ними.
В этом случае стоит воспользоваться вот такой формулой:
Вот и все, что нужно знать о вычислении площади прямоугольников.