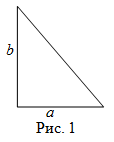Какие размеры известны:
Два катета
Катет и гиппотенуза
Укажите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.
Треугольники бывают прямоугольный, равнобедренный, равносторонний.
Катет — это прилежащая прямому углу сторона треугольника.
Гипотенуза — это сторона треугольника противолежащая прямому углу.
Формула площади прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника, необходимо знать размеры двух сторон треугольника.
Площадь прямоугольного треугольника расчитывается по формуле:
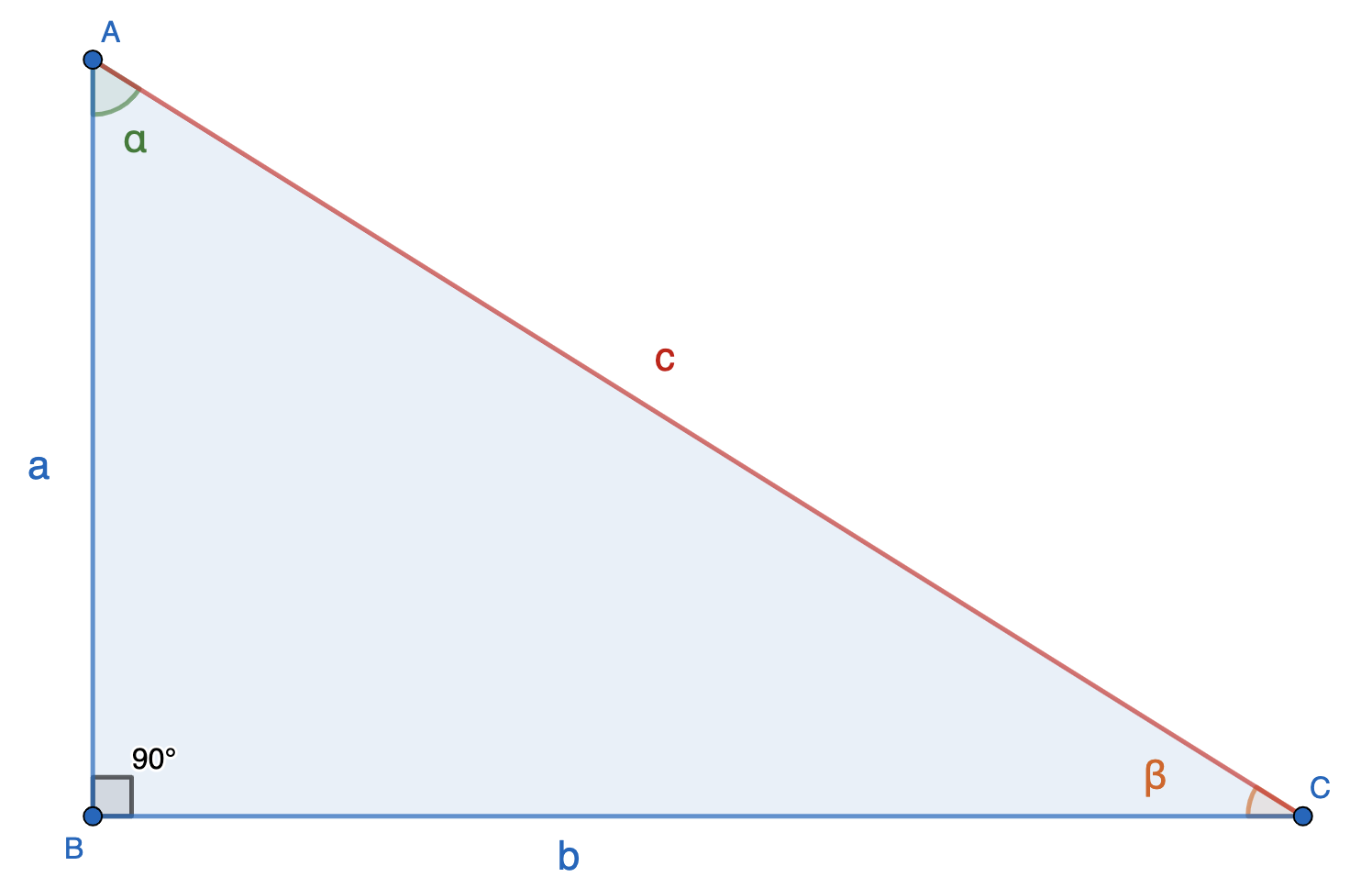
a
b
c
S = dfrac{a cdot b}{2}
- S — площадь треугольника
- a — катет
- b — катет
- c — гипотенуза
Если известены размеры только одного катета и гипотенузы, тогда площадь прямоугольного треугольника можно расчитать по формулам:
S = dfrac{a cdot sqrt{c^2 — a^2}}{2}
S = dfrac{b cdot sqrt{c^2 — b^2}}{2}
Похожие калькуляторы:
Войдите чтобы писать комментарии
Основные определения
Прямоугольный треугольник — это такой треугольник, в котором один из углов равен 90° (прямой угол).
Катеты — стороны, прилежащие к прямому углу 90°.
Гипотенуза — сторона, противолежащая прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно воспользоваться несколькими формулами.
Формула площади прямоугольного треугольника через катеты
(S = {{a*b} over 2})
a, b — катеты
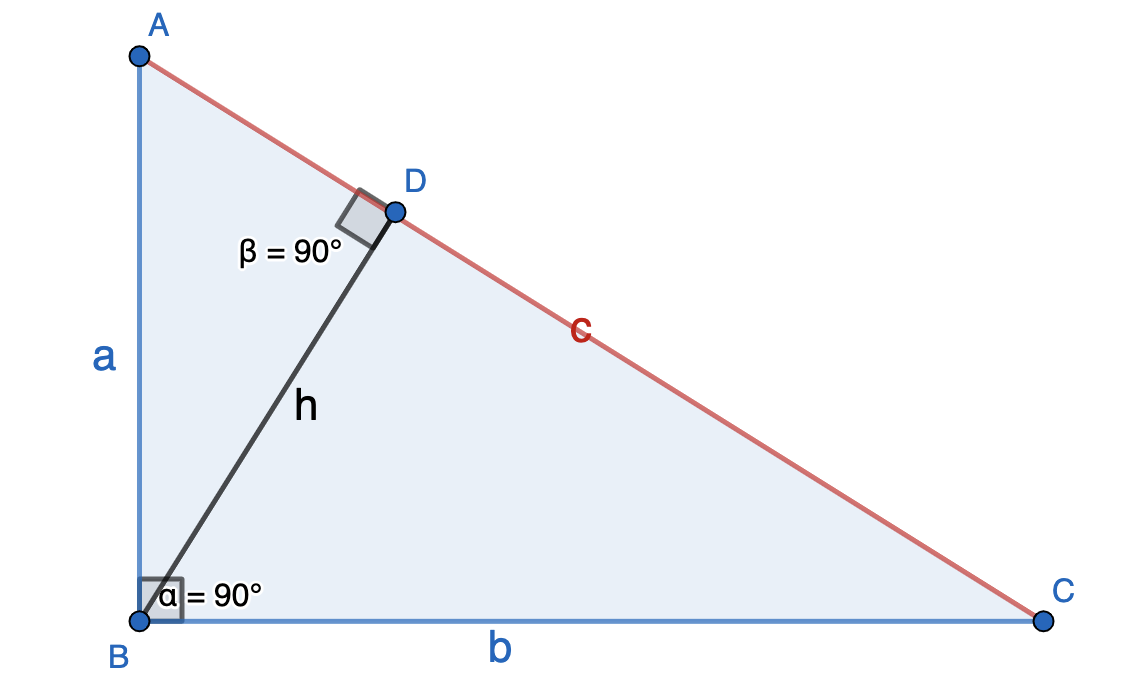
Формула площади прямоугольного треугольника через гипотенузу
(S =1/2(c*h))
(c) — длина гипотенузы,
(h) — высота.
В прямоугольном треугольнике высота находится по формуле:
(h = frac{a*b}{c})
(a) — длина одного катета,
(b) — длина второго катета.
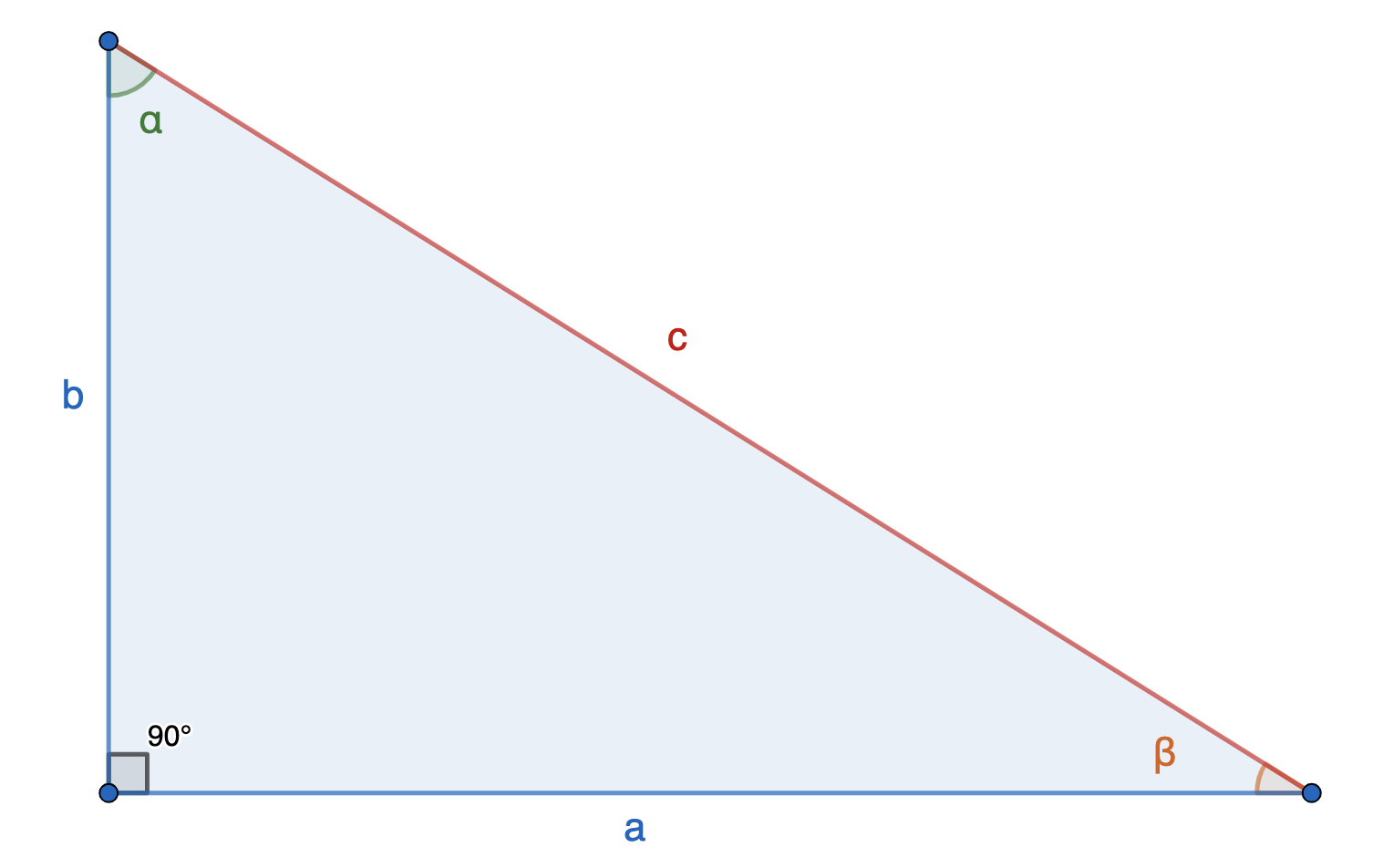
Формула площади прямоугольного треугольника через острый угол и гипотенузу
Если известны острый угол и гипотенуза, то посчитать площадь можно так:
(S = frac{c^2*sinalpha*cosalpha}{2}= frac{c^2*sin(2alpha)}{4})
(S = frac{c^2*sinbeta*cosbeta}{2}= frac{c^2*sin(2beta)}{4})
(c) — гипотенуза
(alpha) и (beta) — острые углы
Формула площади прямоугольного треугольника через катет и острый угол
Если известен один катет и острый угол, то рассчитываем площадь так:
(S = {{a^2*tgbeta} over 2})
(S = {{b^2*tgalpha} over 2})
(a), (b) — катеты
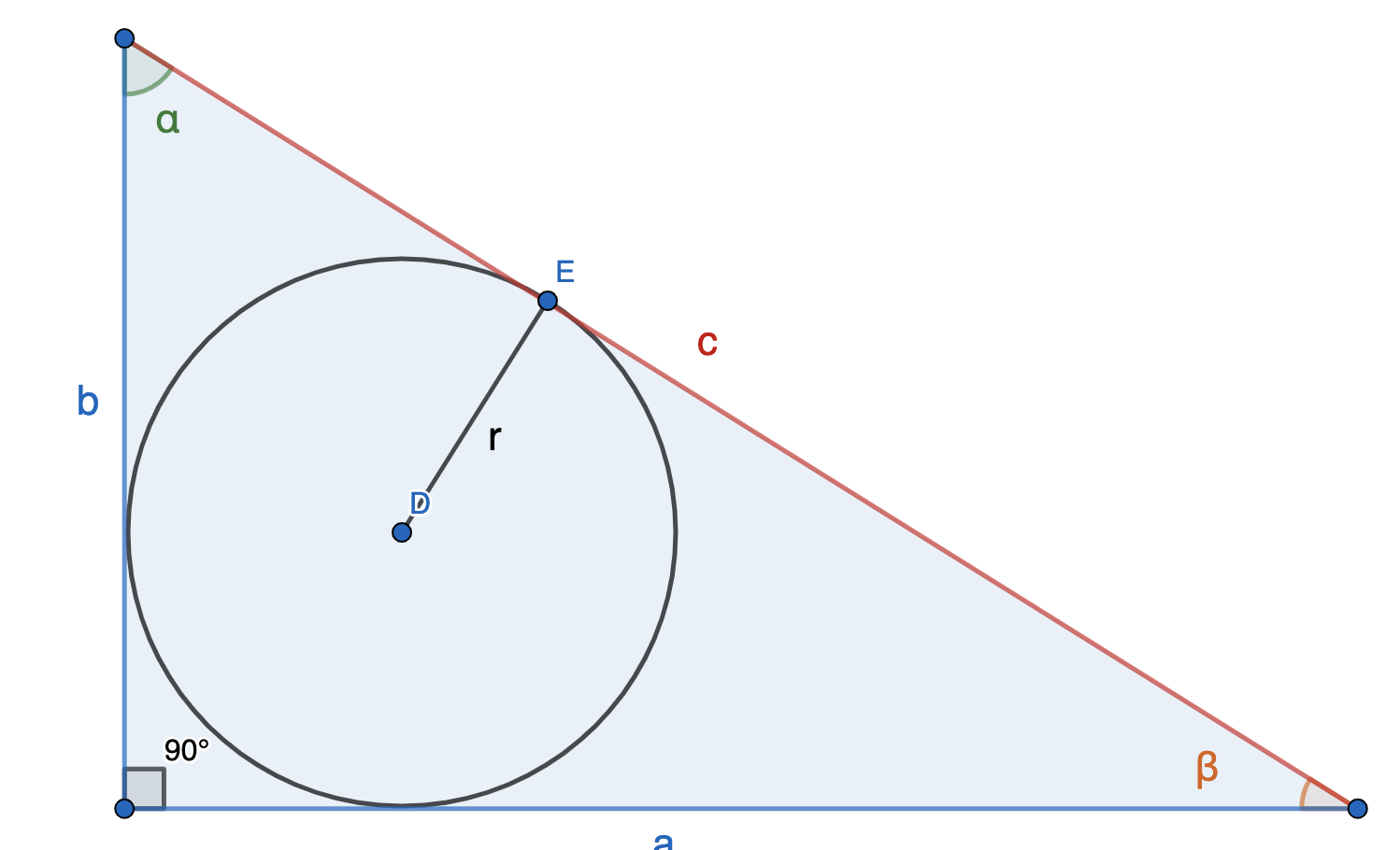
Формула площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
(S = r (r+c))
(r) — радиус вписанной окружности
(с) — гипотенуза
Содержание:
- Формула
- Примеры вычисления площади прямоугольного треугольника
Формула
Чтобы найти площадь прямоугольного треугольника $ABC$ (рис. 1),
надо найти произведение катетов
$a$ и
$b$ и поделить его на два. То есть
$$mathrm{S}_{Delta A B C}=frac{a b}{2}$$
Напомним, что катетами прямоугольного треугольника называются стороны, которые пересекаются под прямым углом.
Примеры вычисления площади прямоугольного треугольника
Пример
Задание. Найти площадь прямоугольного треугольника
$ABC$, если известно, что длины его катетов равны 3 см и 4 см.
Решение. Искомая площадь равна половине произведения катетов, то есть
$mathrm{S}_{Delta A B C}=frac{3 cdot 4}{2}=frac{12}{2}=6$ (см2)
Ответ. $mathrm{S}_{Delta A B C}=6$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить площадь прямоугольного треугольника, один из катетов которого равен 6 см, а гипотенуза 10 см.
Решение. Искомая площадь равна половине произведения катетов. Используя теорему Пифагора,
найдем второй катет заданного треугольника:
$b=sqrt{10^{2}-6^{2}}=sqrt{100-36}=sqrt{64}=8$ (см)
Тогда площадь
$S=frac{6 cdot 8}{2}=frac{48}{2}=24$ (см2)
Ответ. $S=24$ (см2)
Читать дальше: как найти площадь равнобедренного треугольника.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
— полупериметр треугольника; a,b,c — стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a — основание треугольника; h — высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b — стороны треугольника; α — угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a— сторона треугольника; α и β — прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b — катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b — стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a — основание равнобедренного треугольника; α — угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a — сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h — высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r — радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r — радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c — стороны треугольника; r — радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p — полупериметр треугольника;a, b, c — стороны треугольника; r — радиус вписанной окружности треугольника.
Найти площадь прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
0
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
0
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =
0
Введите длину одного из катетов и прилежащий к нему острый угол в градусах.
То есть к катету a прилежащий ∠β, а к катету b — ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
0
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b — ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
0
Введите длину гипотенузы и один из острых угол в градусах.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²