Как найти площадь правильного четырехугольника формула - Avtoru.top

Правильный многоугольник

формулы, признаки и свойства правильного многоугольника
формулы правильного n-угольника
правильный треугольник
правильный четырехугольник
правильный шестиугольник
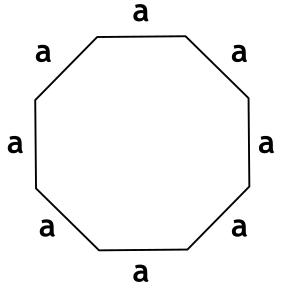
правильный восьмиугольник

Формулы, признаки и свойства правильного многоугольника

Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.

Многоугольники отличаются между собой количеством сторон и углов.

Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.

a1=a2=a3=…=an-1=an

α1=α2=α3=…=αn-1=αn

где a₁…a_n — длины сторон правильного многоугольника,
α₁…α_n — внутренние углы между стронами правильного многоугольника.

Основные свойства правильного многоугольника

Все стороны равны:
a1=a2=a3=…=an-1=an
Все углы равны:
α1=α2=α3=…=αn-1=αn
Центр вписанной окружности O_в совпадает с центром описанной окружности O_о, что и образуют центр многоугольника O.
Сумма всех углов n-угольника равна:180°·n-2
Сумма всех внешних углов n-угольника равна 360°: β1+β2+β3+…+βn-1+βn=360°
Количество диагоналей (D_n) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: Dn = n·n-32
В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π4·a2
Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O.

Формулы правильного n-угольника

Формулы длины стороны правильного n-угольника

Формула стороны правильного n-угольника через радиус вписанной окружности

a = 2·r·tg180°n

(через градусы),

a = 2·r·tgπn

(через радианы)

Формула стороны правильного n-угольника через радиус описанной окружности

a = 2·R·sin180°n

(через градусы),

a = 2·R·sinπn

(через радианы)

Формулы радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны

r = a:2·tg180°n

(через градусы),

r = a:2·tgπn

(через радианы)

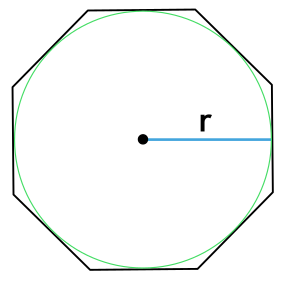
Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны

R = a:2·sin180°n

(через градусы),

R = a:2·sinπn

(через радианы)

Формулы площади правильного n-угольника

Формула площади n-угольника через длину стороны

S = n·a24·ctg180°n

Формула площади n-угольника через радиус вписанной окружности

S = n·r2·tg180°n

Формула площади n-угольника через радиус описанной окружности

S = n·R22·sin360°n

Формула периметра правильного многоугольника

Формула периметра правильного n-угольника

Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.

P = n·a

Формула определения угла между сторонами правильного многоугольника

Формула угла между сторонами правильного n-угольника

αn = n-2n·180°

Правильный треугольник

Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.

Формулы правильного треугольника

Формула стороны правильного треугольника через радиус вписанной окружности

Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.

a = 2·r·3

Формула стороны правильного треугольника через радиус описанной окружности

Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.

a = R·3

r = a·36

R = a·33

Формула площади правильного треугольника через длину стороны

S = a2·34

Формула площади правильного треугольника через радиус вписанной окружности

S = r2·3·3

Формула площади правильного треугольника через радиус описанной окружности

S = R2·3·34

Углы между сторонами правильного треугольника

α1=α2=α3=60°

Правильный четырехугольник

Правильный четырехугольник — это квадрат.

Формулы правильного четырехугольника

Формула стороны правильного четырехугольника через радиус вписанной окружности

Сторона правильного четырехугольника равна двум радиусам вписанной окружности.

a = 2·r

Формула стороны правильного четырехугольника через радиус описанной окружности

Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.

a = R·2

Формула радиуса вписанной окружности правильного четырехугольника через длину стороны

Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.

r = a2

Формула радиуса описанной окружности правильного четырехугольника через длину стороны

Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.

R = a·22

Формула площади правильного четырехугольника через длину стороны

Площадь правильного четырехугольника равна квадрату стороны четырехугольника.

S = a2

Формула площади правильного четырехугольника через радиус вписанной окружности

Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.

S = 4·r2

Формула площади правильного четырехугольника через радиус описанной окружности

Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.

S = 2·R2

Углы между сторонами правильного четырехугольника

α1=α2=α3=α4=90°

Правильный шестиугольник

Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.

Формулы правильного шестиугольник

Формула стороны правильного шестиугольника через радиус вписанной окружности

a = 2·r·33

Формула стороны правильного шестиугольника через радиус описанной окружности

Длина стороны правильного шестиугольника равна радиусу описанной окружности.

a = R

Формула радиуса вписанной окружности правильного шестиугольника через длину стороны

r = a·32

Формула радиуса описанной окружности правильного шестиугольника через длину стороны

R = a

Формула площади правильного шестиугольника через длину стороны

S = a2·3·32

Формула площади правильного шестиугольника через радиус вписанной окружности

S = r2·2·3

Формула площади правильного шестиугольника через радиус описанной окружности

S = R2·3·32

Углы между сторонами правильного шестиугольника

α1=α2=α3=α4=α5=α6=120°

Правильный восьмиугольник

Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.

Формулы правильного восьмиугольника

Формула стороны правильного восьмиугольника через радиус вписанной окружности

a = 2·r·2-1

Формула стороны правильного восьмиугольника через радиус описанной окружности

a = R·2-2

Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны

r = a·2+12

Формула радиуса описанной окружности правильного восьмиугольника через длину стороны

R = a·4+222

Формула площади правильного восьмиугольника через длину стороны

S = a2·2·2+1

Формула площади правильного восьмиугольника через радиус вписанной окружности

S = r2·8·2-1

Формула площади правильного восьмиугольника через радиус описанной окружности

S = R2·2·2

Углы между сторонами правильного восьмиугольника

α1=α2=α3=α4=α5=α6=α7=α8=135°

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

Источник

Площадь четырехугольника

Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

Площадь четырехугольника по диагоналям и углу между ними

Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Таблица с формулами площади четырехугольника

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	диагональ и угол между ними
2	стороны и углы между этими сторонами
3	стороны (по Формуле Брахмагупты)
4	стороны и радиус вписанной окружности
5	стороны и углы между ними

Площадь частных случаев четырехугольников

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Как рассчитать площадь четырехугольника

На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.

Через диагонали и угол между ними

Формула для нахождения площади четырехугольников через диагонали и угол между ними:

Через стороны и противолежащие углы

Формула для нахождения площади четырехугольников через стороны и противолежащие углы:

Площадь вписанного четырехугольника в окружность

Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:

Площадь описанного четырехугольника около окружности через радиус

Формула для нахождения площади описанного четырехугольника около окружности через радиус:

Калькулятор расчета площади четырехугольника

В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через диагонали и угол между ними

Формула расчета

2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

Формула расчета

p – полупериметр четырехугольника, равняется:

источники:

http://www.mozgan.ru/Geometry/ArearQuadrangle

Калькулятор расчета площади четырехугольника

Источник

Download Article

Quickly calculate the area of any 4-sided figure, including squares, rectangles, parallelograms, kites, and rhombuses

Download Article

Area of Trapezoid and Kite Cheat Sheets

Square

Rectangle

Parallelogram

Trapezoid

Rhombus

Kite

Any Quadrilateral Shape

Tips

If you’re stuck on your geometry homework trying to figure out the area of a quadrilateral, you’ve come to the right place! Remember—the «area» of a shape is just how much 2-dimensional space it takes up. For some quadrilaterals, there’s a handy formula you can use to calculate the area. But what if all the sides are different? Just divide it into triangles! Read on to follow along with some examples and see how this works.

Things You Should Know

Area of Square, Rectangle, and Rhombus Cheat Sheets

Area of Trapezoid and Kite Cheat Sheets

Use ${displaystyle A=s^{2}}$ to find the area of a square. In the formula, «s» is the length of one side. Since all sides are equal, you only need the length of one of them to quickly find the area of any square. Then, express the area in units squared.

Use the formula to find the area of a rectangle. Since a rectangle has sides of 2 different lengths, you multiply one value by the other to find out how much space the rectangle covers. Just get the length of one of the short sides and one of the long sides.

Find the area of a parallelogram with . A parallelogram has 2 parallel sides—those are the bases (b). The height (h) is the distance from one base to the other. Multiply those 2 values together and you’ve got the area of a parallelogram.^[1]

Use ${displaystyle A={frac {b_{1}+b_{2}}{2}}*h}$ to calculate a trapezoid’s area. Since the 2 bases (b) of a trapezoid aren’t the same length, the average is used for the area of this shape. Once you have the average length of the two bases, multiply that by the height (h)—the distance between the two bases—to easily find the area of a trapezoid.^[2]

Find the area of a kite with ${displaystyle A={frac {(d_{1}*d_{2})}{2}}}$ . A kite’s orientation can throw you off because your «diagonal» lines (d1 and d2) might not look diagonal at all—they might actually be vertical and horizontal. But as long as they’re connecting opposing corners, they’re still called diagonals. Multiply them together and then divide by to get your area.

1
Divide the quadrilateral into 2 triangles. If you draw a diagonal line from one corner to the other, you create 2 triangles within the quadrilateral. The 2 triangles might not be the same size, but they share a common base—the diagonal that divides the quadrilateral.^[4]
- If you’re working on a homework problem, the diagonal line might already be drawn for you. In fact, if you have a quadrilateral with a diagonal line, that’s a pretty big clue that you’ll use triangles to find the area.
2
Get the measurements for the base and heights of your triangles. To find the area of a triangle, you need to know the size of the base (b) and the height (h). Your diagonal line is serving as the base of your triangles, so they’ll both have the same measurement for the base. They might not be the same height, though, depending on the quadrilateral. The height isn’t the length of a side (unless you’re working with a right triangle). It’s the length from the base to the top point of the triangle.^[5]
- If you’re working a problem for homework and you’re not given any way to measure these values, you can’t use triangles to find the area of that quadrilateral.
3

Find the area of each triangle. Recall that the formula for the area of a triangle is $A={frac {1}{2}}bh$ . All you have to do is plug in the measurements you got for the base and the height, then simplify the equation to find the area of each triangle.^[6]
4

Add the areas of the 2 triangles together to get the area of the quadrilateral. Since you originally divided your quadrilateral into 2 triangles, all you have to do is add those 2 areas together and you’ll have the total area of the quadrilateral. You could also think of the area of one of the triangles as being half the area of the quadrilateral.^[7]

Add New Question

Question

Could I divide the quadrilateral into two triangles, find the area of each, and add them to find the area of the quadrilateral?

Yes. If you know the base and height of each triangle, you can just add the two areas together. It’s not always possible, however, to know the bases and heights.
Question

How do I calculate the area of a parallelogram?

Calculate as follows: Area = base multiplied by height.
Question

How would I know the angle for quadrilateral?

Assuming you’re not given the angle(s), you either have to use a protractor or analyze the quadrilateral and use trigonometry.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Since a square is also a rhombus, if you only know the measurement of a diagonal, you can also find the area of a square using the rhombus formula.

References

About This Article

Article SummaryX

Before you can find the area of a regular quadrilateral, start by identifying the type of quadrilateral in the problem, since different types of quadrilaterals require different equations. For rectangles or rhombuses, simply multiply the base by the height to find the area. For squares, multiply one side by itself to get the area. If you have a parallelogram, multiply the diagonals and divide by 2 to get the area. To find the area of a trapezoid, add the base and the height together, and divide that number by 2 times the height. If you want to find the area of an irregular quadrilateral, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,699,793 times.

Reader Success Stories

«Great, but I would be glad if you could find the angles for any quadrangular with given sides. But you put some…» more

Did this article help you?

Источник

На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

Формула площади правильного многоугольника через длину стороны и число сторон

S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a — длина стороны многоугольника

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус вписанной окружности

S = nr^2 tg dfrac{180°}{n}

r — радиус вписанной в многоугольник окружности

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R — радиус описанной в многоугольник окружности

n — число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r — радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

Правильный четырехугольник

Правильный четырехугольник — это такой четырехугольник у которого все четыре стороны равны и его четыре угла равны. Правильный четырехугольник это квадрат.

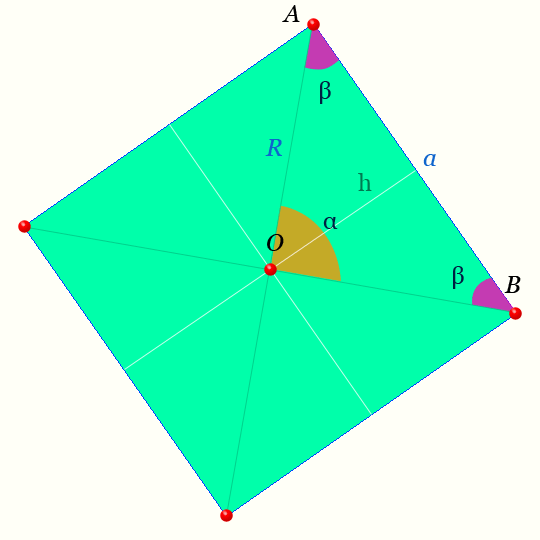
Правильный четырехугольник

Центр правильного четырехугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного четырехугольника.

Обозначения на рисунке для правильного четырехугольника

n=4	число сторон и вершин правильного четырехугольника,	шт
α	центральный угол правильного четырехугольника,	радианы, °
β	половина внутреннего угла правильного четырехугольника,	радианы, °
γ	внутренний угол правильного четырехугольника,	радианы, °
a	сторона правильного четырехугольника,	м
R	радиусы правильного четырехугольника,	м
p	полупериметр правильного четырехугольника,	м
L	периметр правильного четырехугольника,	м
h	апофемы правильного четырехугольника,	м

Основные формулы для правильного четырехугольника

Периметр правильного четырехугольника

[ L = 4a ]

Полупериметр правильного четырехугольника

[ p = 2a ]

Центральный угол правильного четырехугольника в радианах

[ α = frac{π}{2} ]

Центральный угол правильного четырехугольника в градусах

[ α = frac{360°}{4} = 90° ]

Половина внутреннего угла правильного четырехугольника в радианах

[ β = frac{π}{4} ]

Половина внутреннего угла правильного четырехугольника в градусах

[ β = frac{180°}{4} = 45° ]

Внутренний угол правильного четырехугольника в радианах

[ γ = 2β = frac{π}{2} ]

Внутренний угол правильного четырехугольника в градусах

[ γ = frac{180°}{2} = 90° ]

Площадь правильного четырехугольника

[ S = ph = 2ha ]

Или учитывая формулу Площади квадрата получим

[S=a^2]

Правильный четырехугольник	стр. 268

Источник