
Задачи с решениями
-
Найти площадь части сферы
заключенной внутри цилиндра
Решение Из уравнения сферы имеем
(для I октанта):
областью интегрирования D.
Поверхность расположена в четырех
октантах потому искомая площадь
Перейдем к полярным координатам, тогда
уравнение окружности примет вид
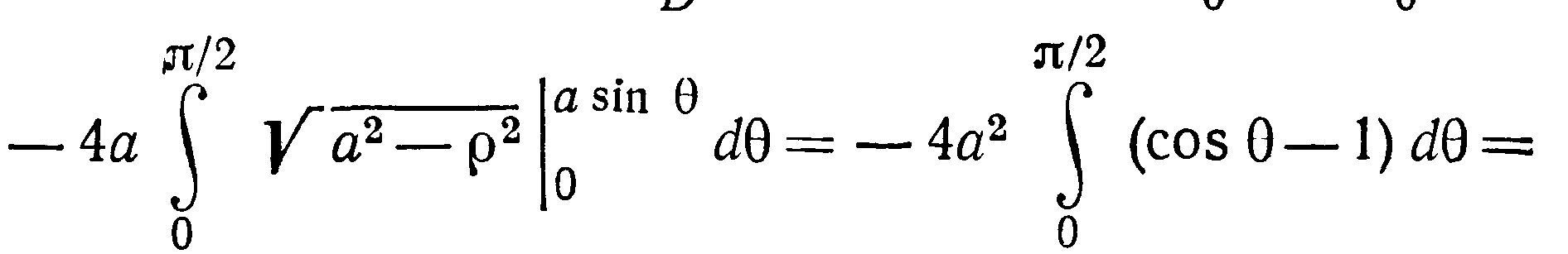
-
Найти площадь части конуса
внутри цилиндра
Решение Из уравнения конуса
имеем
Областью
интегрирования D является круг,
ограниченный окружностью
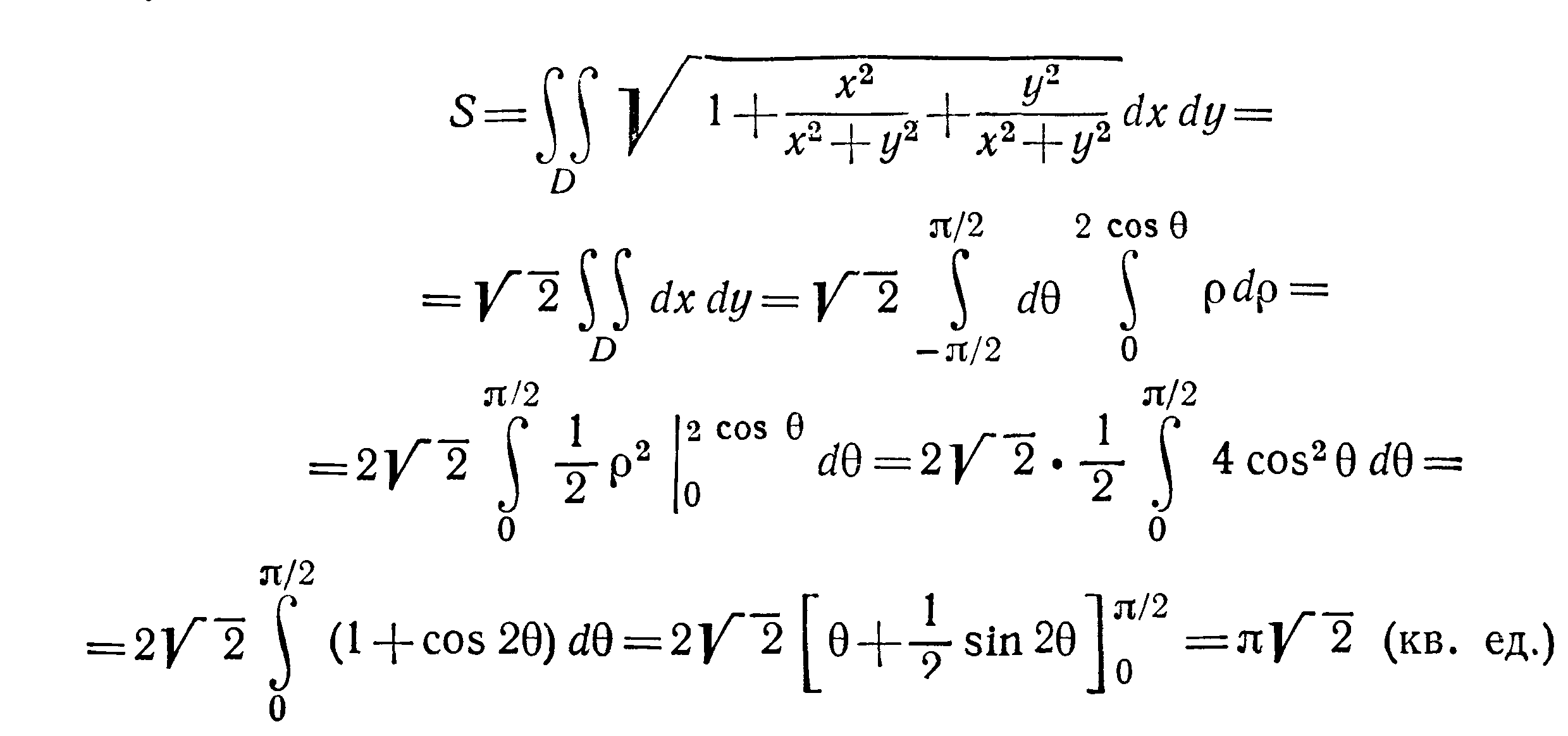
-
Вычислить площадь поверхности цилиндра
отсеченной плоскостями
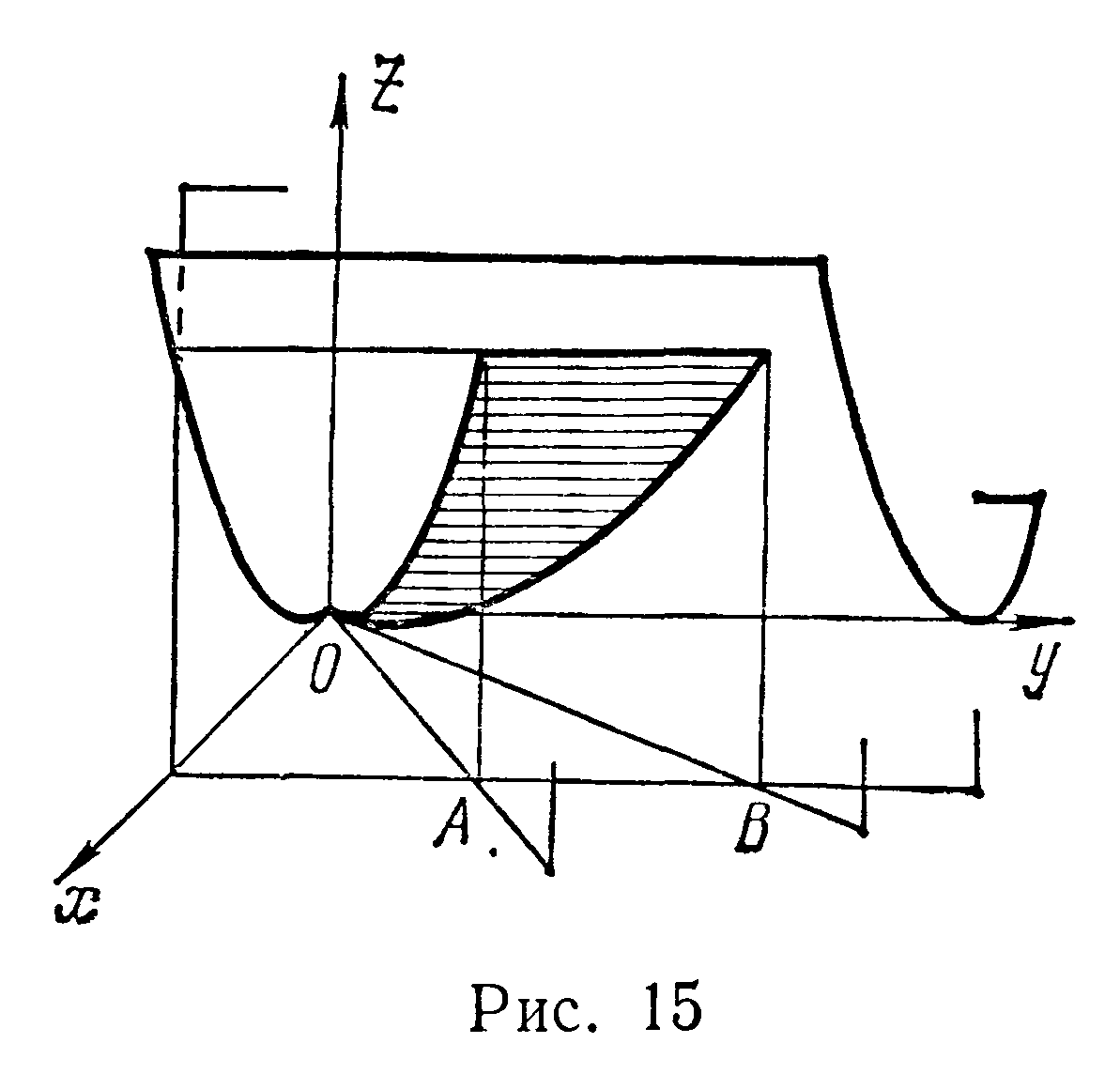
Решение Областью интегрирования
служит треугольник ОАВ. Из уравнения
цилиндра имеем
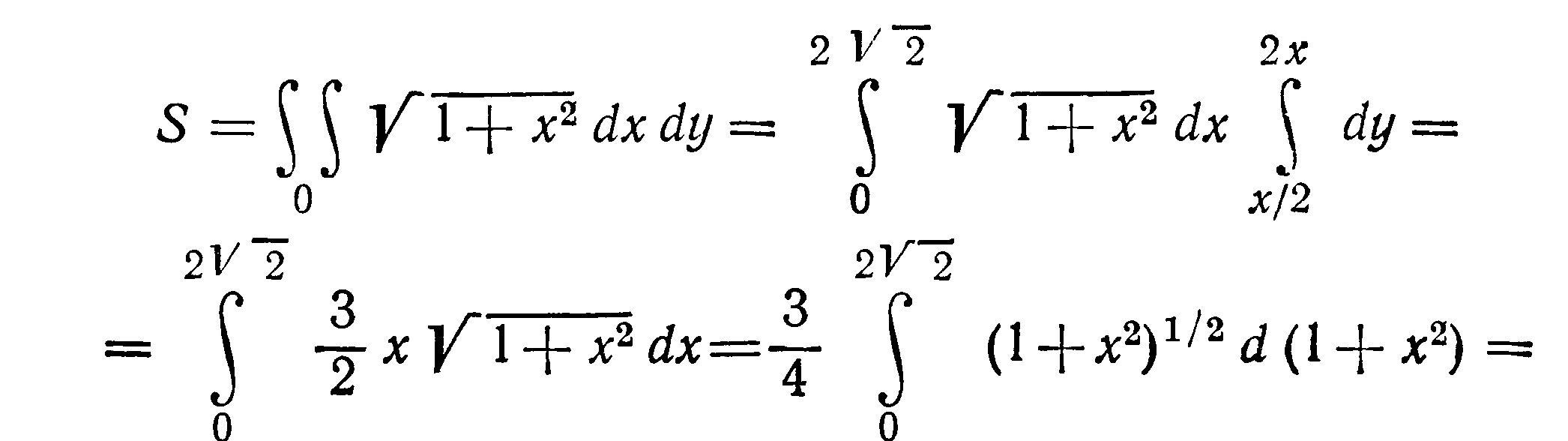
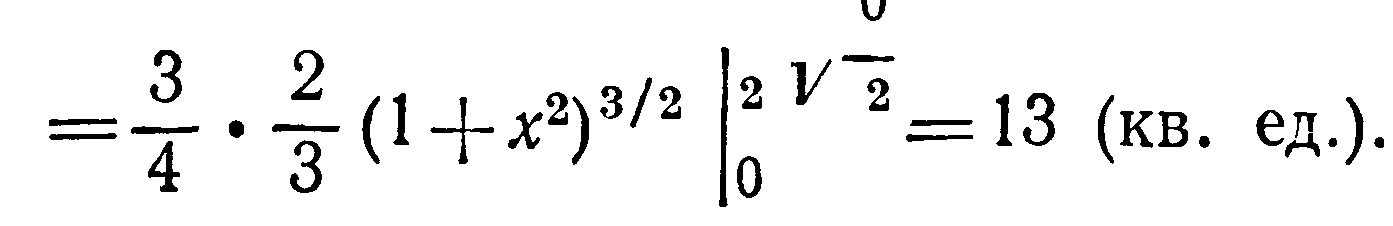
-
Вычислить площадь части поверхности
параболоида x
,
вырезанной цилиндром
Решение Область интегрирования
— окружность
(она расположена в плоскости yOz).
Из уравнения параболоида имеем
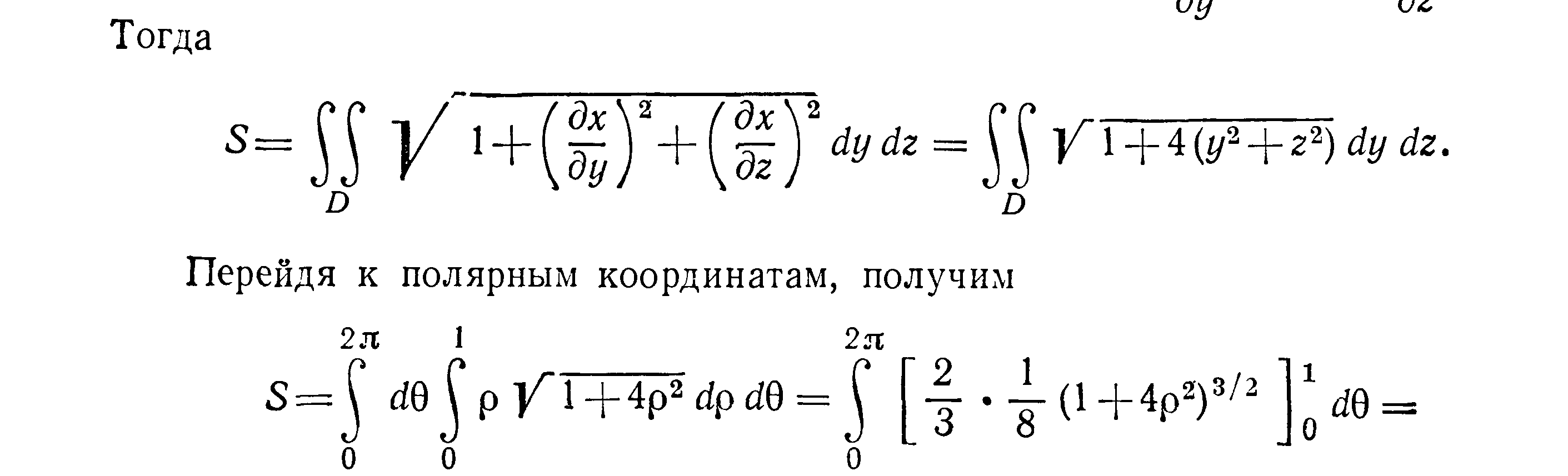
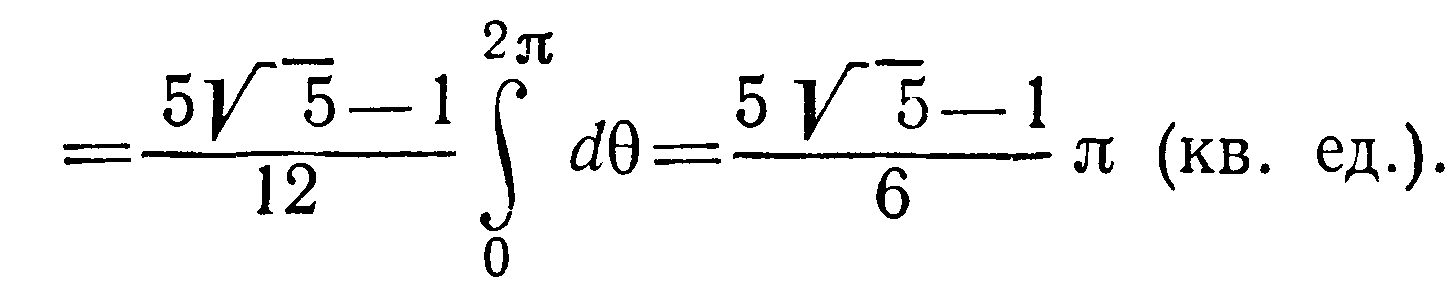
Задачи
36 . Найти площадь части поверхности
вырезанной цилиндром
37. Найти площадь части сферы
вырезанной цилиндром
38. Найти площадь той части плоскости z=
x:, которая заключена
внутри цилиндра
39. Найти площадь части поверхности
цилиндра z = x2,
вырезанной плоскостями
40. Вычислить площадь поверхности конуса
расположенной внутри цилиндра
41. Вычислить площадь поверхности цилиндра
расположенной внутри цилиндра
42. Найти площадь части поверхности
вырезанной плоскостями
Индивидуальные задания


Тройной интеграл
Пусть функция f (х, у, z)
определена в ограниченной замкнутой
пространственной области Т. Разобьем
область Т произвольным образом на п
элементарных областей T1
Т2, …, Тn с
диаметрами d1 d2,
…, dn и объемами ∆V1,
∆V2, ….,∆Vn.
В каждой элементарной области возьмем
произвольную точку Pk
(ξ1, ξ2, … , ξn
) и умножим значение функции в точке Рk
на объем этой области.
Интегральной суммой для функции f
(х, у, z) по области Т
называется сумма вида
Предел интегральной суммы при стремлении
к нулю наибольшего из диаметров всех
элементарных областей ∆Vk
называется тройным интегралом от функции
f (х, у, z) по
области Т и обозначается следующим
образом:
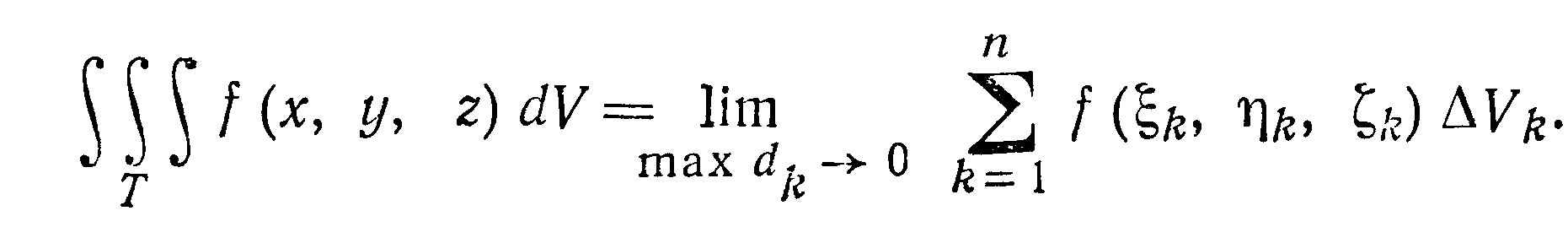
Конечный предел такого вида может
существовать только для ограниченной
функции.
Если f (х, у, z)
> 0 в области Т, то тройной интеграл
представляет собой массу тела, занимающего
область Т и имеющего переменную плотность
γ = f(x, у, z)
(физическое истолкование тройного
интеграла).
Основные свойства тройных интегралов
аналогичны свойствам двойных интегралов.
В декартовых координатах тройной
интеграл обычно записывают в виде
Пусть область интегрирования Т
определяется неравенствами x1≤
x≤ x2, y1≤
y ≤ y2,
z1≤ z
≤ z2, где y1(x),
y2(x),
z1(x,y),
z2 (x,y)
непрерывные функции. Тогда тройной
интеграл от функции f (х,
у, z), распространенный на область Т,
вычисляется по формуле
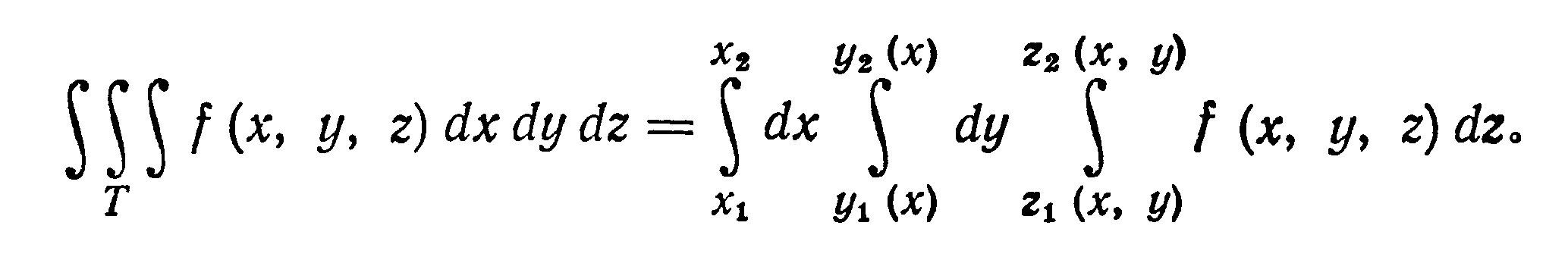
Если при вычислении тройного интеграла
требуется перейти от переменных х, у, z
к новым переменным и, v, w, связанным с х,
у, z соотношениями х = х(u,
v, w), y = y(u, v, w), z = z (u, v, w), где
функции х(и, v, w), y(u,v, w) z (u, v, w), непрерывные
вместе со своими частными производными
первого порядка, устанавливают взаимно
однозначное и в обе стороны непрерывное
соответствие между точками области Т
пространства Oxyz и точками некоторой
области Т’ пространства Ouvw и якобиан J
в области Т’ не обращается в нуль
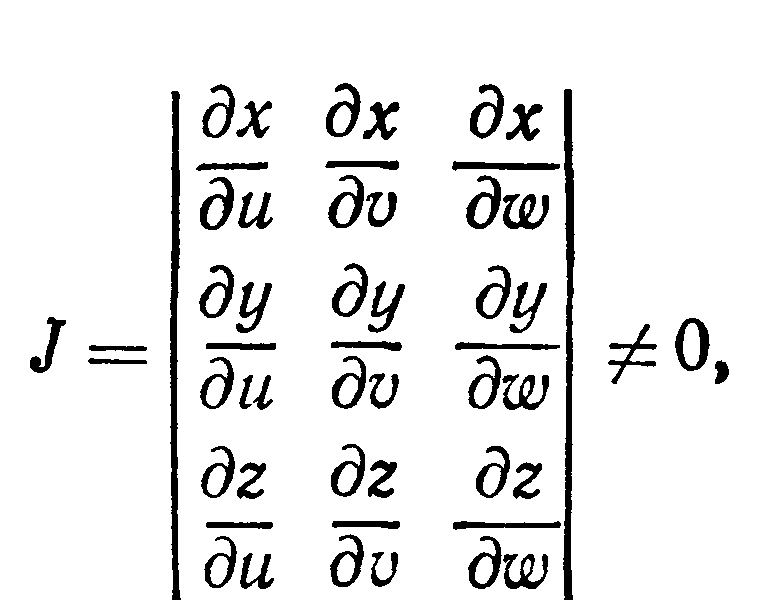
то пользуются формулой
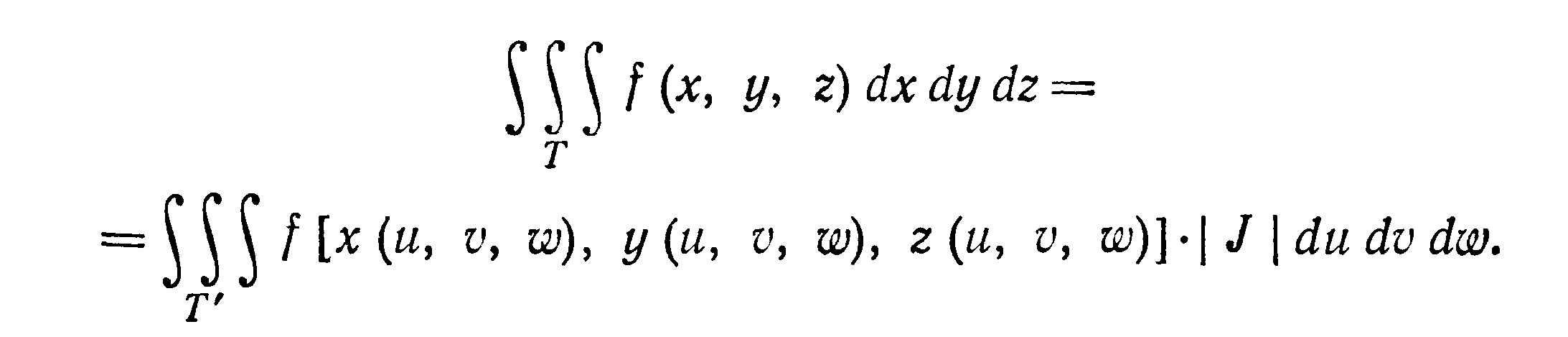
В частности, при переходе от декартовых
координат х, у, z к
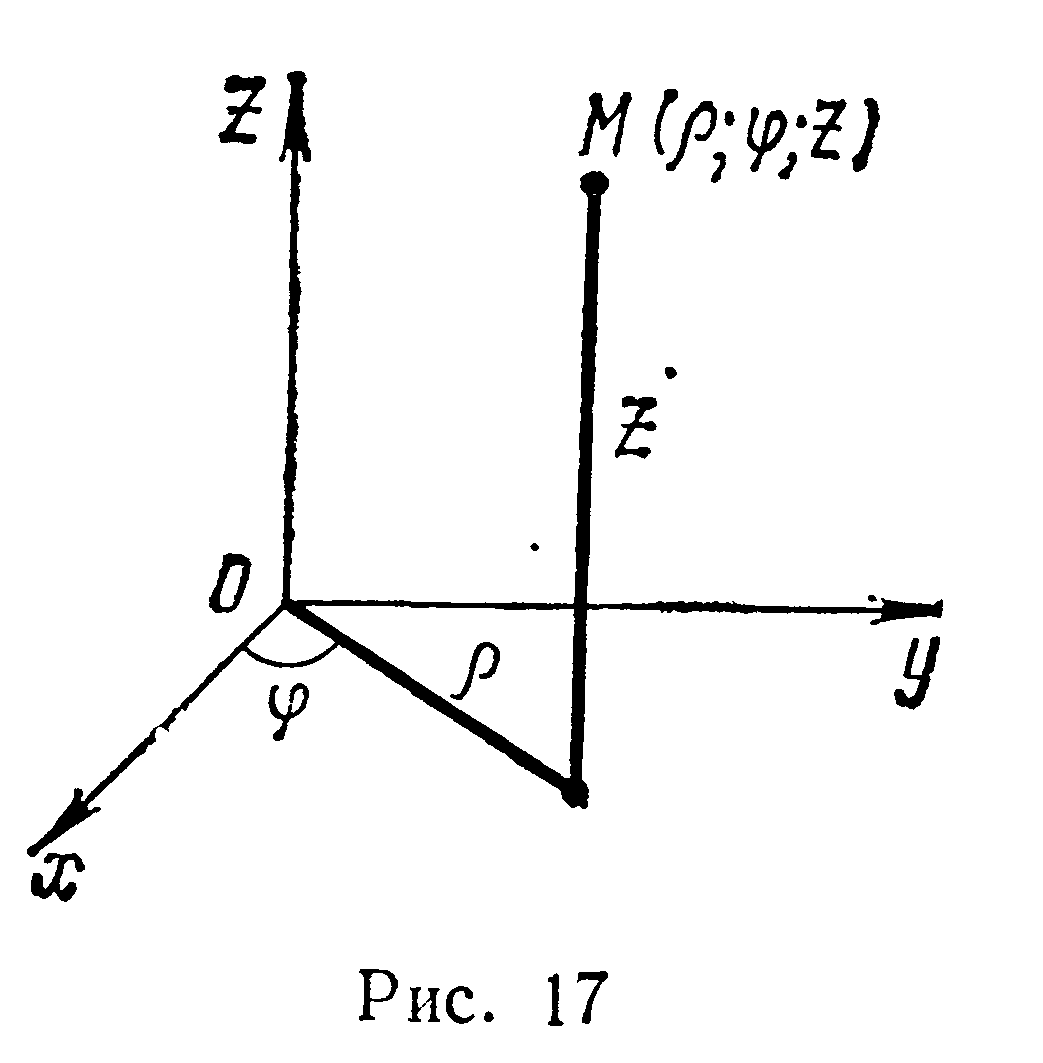
цилиндрическим координатам ρ,φ , z
(рис. 17), связанным с х, у, z
соотношениями
якобиан преобразования J = ρ
и формула преобразования тройного
интеграла
к цилиндрическим координатам имеет вид
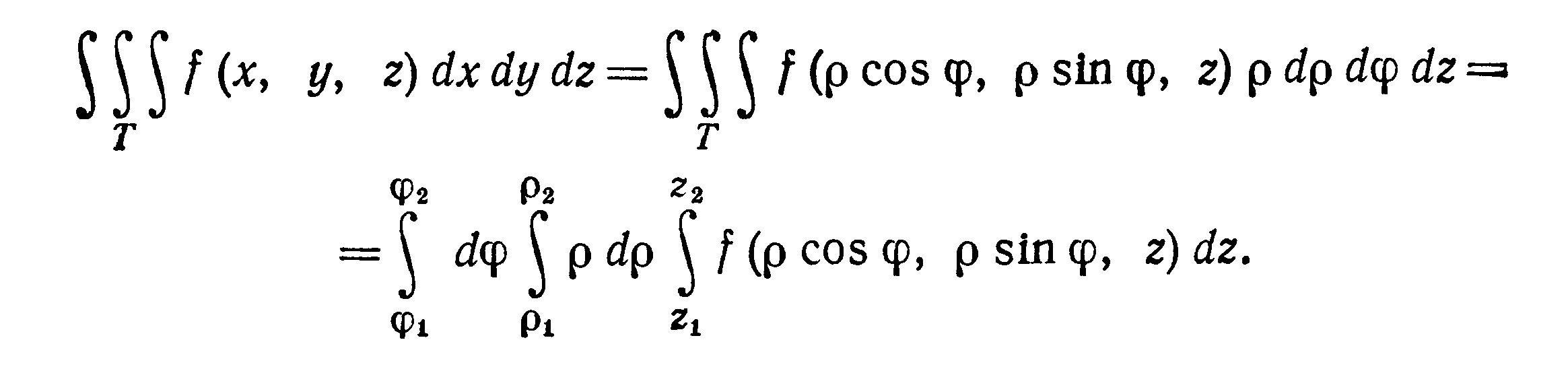
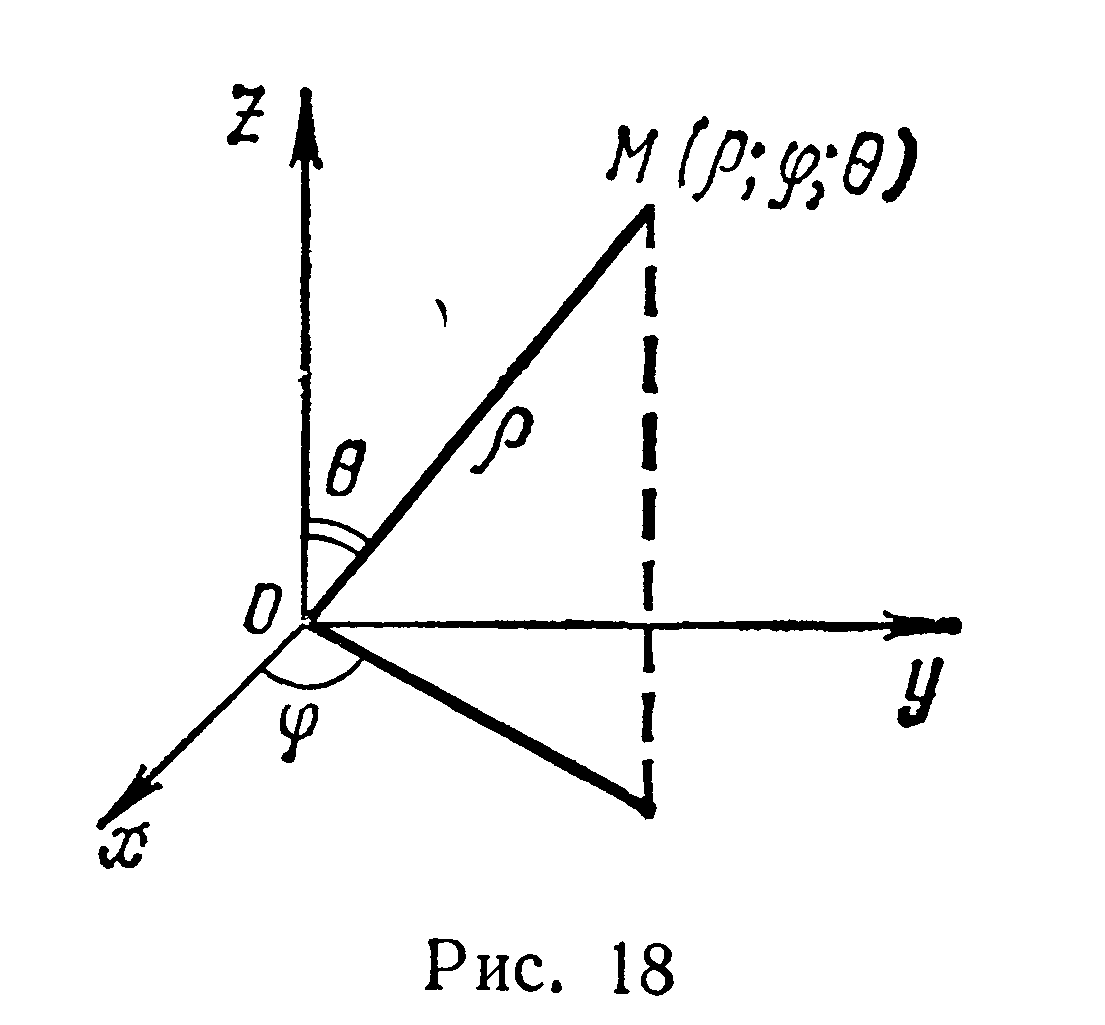
При переходе от декартовых координат
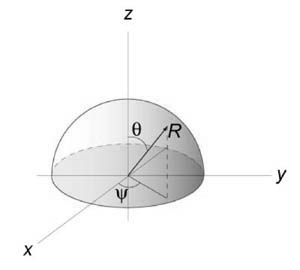
х, у, z к сферическим координатам ρ,φ,θ
(рис. 18), связанным с х, у, z соотношениями
якобиан преобразования J
= ρ2 sinθ, и формула
преобразования тройного интеграла к
сферическим координатам имеет вид
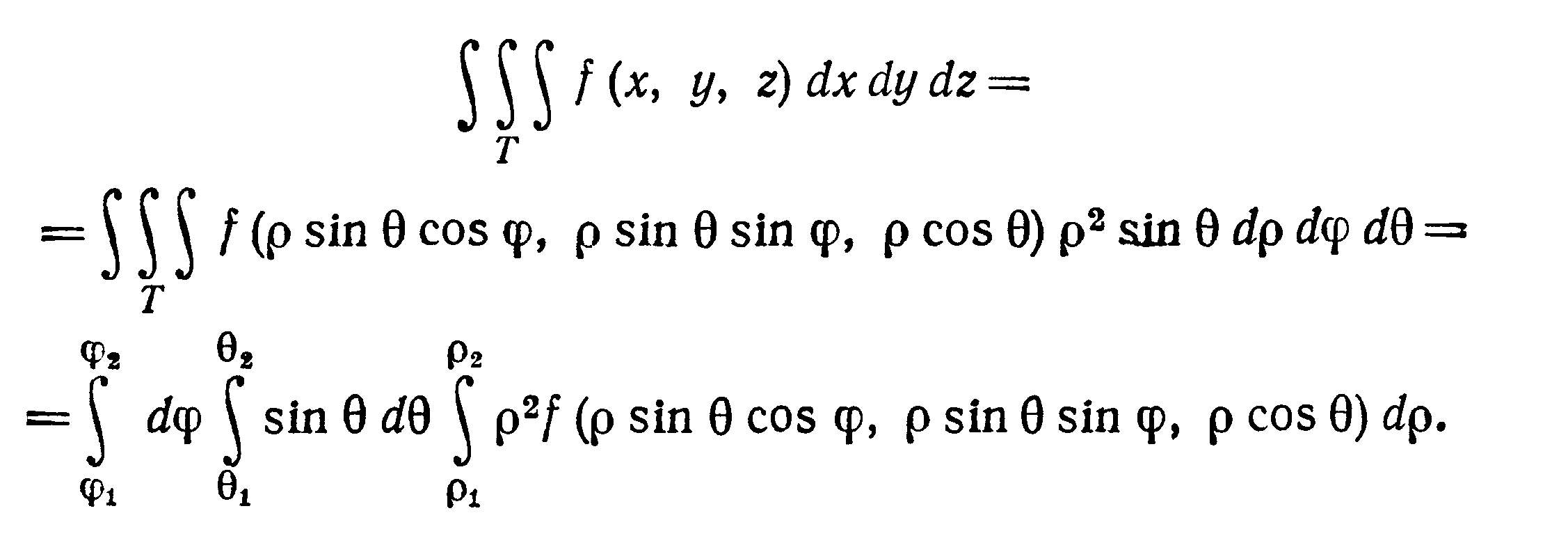
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Случай явного задания поверхности. Площадь


Где
Если поверхность имеет уравнение вида

Где
Если поверхность задана уравнением,

Где
Случай неявного задания поверхности. Площадь


Где
Случай параметрического задания поверхности. Если поверхность задана параметрическими уравнениями
Где
Функции х, у, z непрерывно дифференцируемы, то
(19.24)
Где

Пример 19.17. Найти площадь части поверхности цилиндра 

Ность «тела Вивиани», рис. 19.19).
Применим формулу (19.20). Поскольку плоскостью





Так как
Уравнение параболы, лежащей в плоскости 




Параболывместе с соответствующим отрезком оси
Пример 19.18. Вычислить площадь поверхности конуса 



Ишь

Так как для рассматриваемой части конуса
То по формуле (19.19)
Получаем
Где

Следовательно, вся искомая площадь
Пример 19.19. Найти площадь поверхности, вырезанной цилиндром 
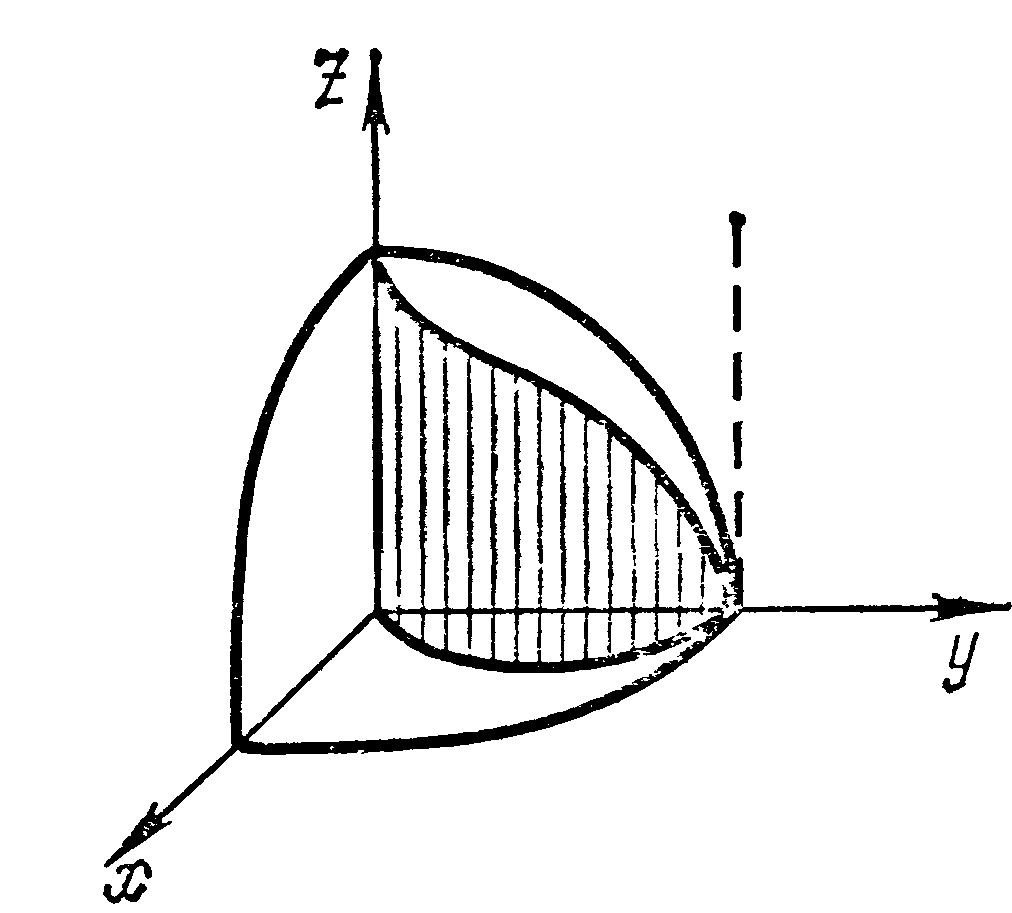
Цилиндр вырезает из сферы две части, верхняя из них изображена на рис. 19.21. Вычислим площадь
Следовательно,
Переходя к полярным координатам, находим 338
Итак,
Рис. 19.20
Пример 19.20. Вычислить площадь частей сферы

Уравнениями сферической поверхности:
Рис. 19.21
Здесь вдет речь о вычислении площади верхнего и нижнего оснований «тела Вивиани» (см. рис. 19.19). Воспользуемся формулой (19.24), для чего предварительно найдем коэффициенты

Находим
Ограничимся рассмотрением четверти изучаемой поверхности, лежащей в первом октанте. Для точек «кривой Вивиани», т. е. кривой пересечения сферы и цилиндра (в пределах первого октанта),







Установив на основании сказанного пределы изменения

| < Предыдущая | Следующая > |
|---|
Вычисление площади поверхности
Пример 1
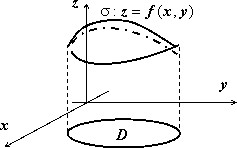
Пусть в пространстве задана кусочно-гладкая поверхность $sigma $, однозначно проектирующаяся в область $mathbf { textit { D } } $ на плоскости $mathbf { textit { Оху } } $. Пусть эта поверхность задаётся уравнением $sigma :;z=f(x,y),;(x,y)in D$. Тогда площадь этой поверхности выражается формулой
$ s(sigma )=iintlimits_D { sqrt { 1+left( { frac { partial f } { partial x } }right)^2+left( { frac { partial f } { partial y } }right)^2 } dxdy } . $
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } $ = 2$mathbf { textit { ax } } $ из сферы $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $ = 4$mathbf { textit { a } } ^ { 2 } $ .
Решение:
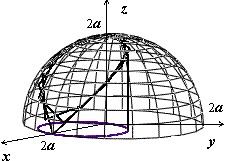
На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $frac { partial z } { partial x } =-frac { x } { sqrt { 4a^2-x^2-y^2 } } , quad frac { partial z } { partial y } =-frac { y } { sqrt { 4a^2-x^2-y^2 } } ,$ и $s(sigma )=iintlimits_D { sqrt { 1+frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2aiintlimits_D { frac { dxdy } { sqrt { 4a^2-x^2-y^2 } } } $.
Область $mathbf { textit { D } } $ — сдвинутый на $mathbf { textit { а } } $ единиц по оси $mathbf { textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $mathbf { textit { Оху } } $ и $mathbf { textit { Охz } } $:
$s(sigma )=4cdot 2aiintlimits_ { D_ { r,varphi } } { frac { rdrdvarphi } { sqrt { 4a^2-r^2 } } } =8aintlimits_0^ { pi /2 } { dvarphi intlimits_0^ { 2acos varphi } { left( { 4a^2-r^2 }right)^ { -1/2 } rdr } } =-8aintlimits_0^ { pi /2 } { dvarphi left. { left( { 4a^2-r^2 }right)^ { 1/2 } }right|_0^ { 2acos varphi } } = \ =8aintlimits_0^ { pi /2 } { left[ { 2a-2asqrt { 1-cos ^2varphi } }right]dvarphi } =16a^2left. { left( { varphi +cos varphi }right) }right|_0^ { pi /2 } =16a^2left( { pi /2-1 }right)$.
Пример 2
Вычислить площадь cферы радиуса (a.)
Решение:
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } ;; { text { или } ;;z = sqrt { { a^2 } — { x^2 } — { y^2 } } . } $
Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } .$
Найдем частные производные. $ { frac { { partial z } } { { partial x } } } = { frac { partial } { { partial x } } sqrt { { a^2 } — { x^2 } — { y^2 } } } = { frac { { — { 2 } x } } { { { 2 } sqrt { { a^2 } — { x^2 } — { y^2 } } } } } = { — frac { x } { z } , } $ $ { frac { { partial z } } { { partial y } } } = { frac { partial } { { partial y } } sqrt { { a^2 } — { x^2 } — { y^2 } } } = { frac { { — { 2 } y } } { { { 2 } sqrt { { a^2 } — { x^2 } — { y^2 } } } } } = { — frac { y } { z } . } $
Подставляя найденные производные, получаем $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } } = { iintlimits_R { sqrt { 1 + frac { { { x^2 } } } { { { z^2 } } } + frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { sqrt { frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { frac { a } { z } dxdy } . } $
Преобразуем двойной интеграл в полярные координаты. $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { frac { a } { z } dxdy } } = { intlimits_0^ { 2pi } { intlimits_0^a { frac { a } { { sqrt { { a^2 } — { r^2 } } } } rdrdtheta } } } = { aintlimits_0^ { 2pi } { dtheta } intlimits_0^a { frac { { rdr } } { { sqrt { { a^2 } — { r^2 } } } } } } = { — 2pi aintlimits_0^a { frac { { dleft( { { a^2 } — { r^2 } }right) } } { { 2sqrt { { a^2 } — { r^2 } } } } } } = { — 2pi aleft. { left( { sqrt { { a^2 } — { r^2 } } }right) }right|_ { r = 0 } ^a } = { — 2pi aleft( { 0 — a }right) = 2pi { a^2 } . } $
Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { largefrac { 1 } { 2 } normalsize } } = 4pi { a^2 } .$
|
1 / 1 / 1 Регистрация: 13.02.2011 Сообщений: 179 |
|
|
1 |
|
Найти площадь части поверхности, вырезанной поверхностями10.03.2012, 15:06. Показов 18947. Ответов 7
Найти площадь части поверхности Мне бы только рисунок и найти пределы интегрирования, а то пространственного представления совсем нет. И специальной программы для построения графиков также нет возможности установить. Возможно там следует перейти к какой-то другой системе координат, но точно не знаю.
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
10.03.2012, 15:41 |
2 |
|
1 |
|
1 / 1 / 1 Регистрация: 13.02.2011 Сообщений: 179 |
|
|
10.03.2012, 16:00 [ТС] |
3 |
|
vetvet, Спасибо конечно, я это знаю, я не знаю просто, как задать пределы интегрирования, там должно быть с тройным интегралом… похоже…
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
10.03.2012, 16:14 |
4 |
|
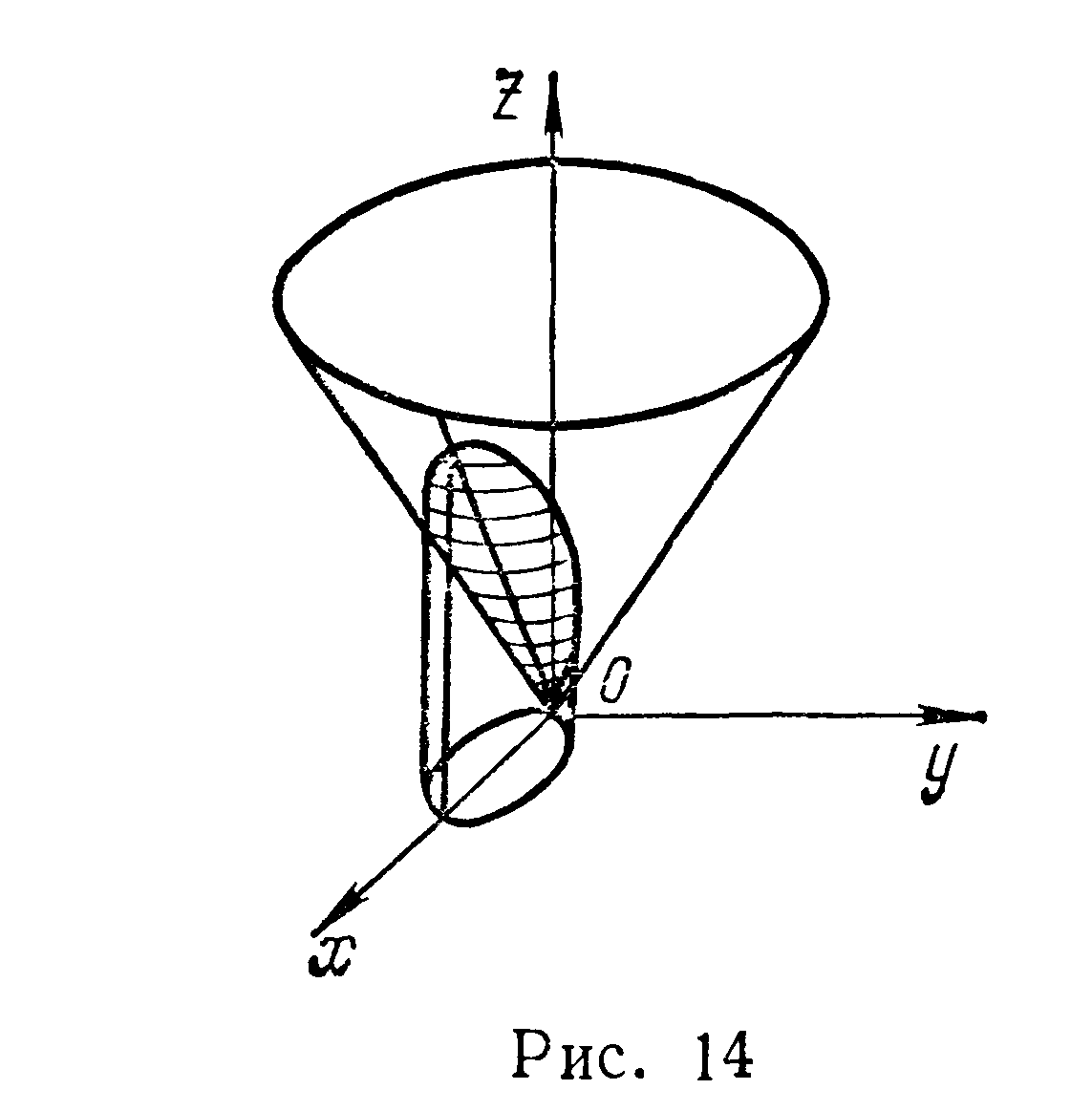
У вас получится вот такое в сечении плоскостями, параллельными плоскости Oxy:
А сверху и снизу оно будет ограничено конусом.
1 |
|
1 / 1 / 1 Регистрация: 13.02.2011 Сообщений: 179 |
|
|
10.03.2012, 16:21 [ТС] |
5 |
|
vetvet, Спасибо большое!!!!!!=)))
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
10.03.2012, 16:27 |
6 |
|
Невнимательно посмотрела. Написала нахождение объёма, а тут нужно площадь куска поверхности. Она вычисляется с помощью двойного интеграла по границам нарисованной области, а подынтегральная функция берётся:
1 |
|
1 / 1 / 1 Регистрация: 13.02.2011 Сообщений: 179 |
|
|
10.03.2012, 18:30 [ТС] |
7 |
|
vetvet, а причом здесь частные производные?? мы на занятиях их не использовали… Добавлено через 1 час 24 минуты
0 |
|
Змеюка одышечная 9863 / 4594 / 178 Регистрация: 04.01.2011 Сообщений: 8,556 |
|
|
10.03.2012, 18:37 |
8 |
|
Потому, что так находится площадь куска поверхности.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
10.03.2012, 18:37 |
|
8 |
Случай явного задания поверхности. ПлощадьГладкой поверхности Выражается формулой
(19.19)
Где- проекция данной поверхности на плоскость
Если поверхность имеет уравнение видаТо
(19.20)
Где— проекция поверхности на ось
Если поверхность задана уравнением,, то
(19.21)
Где— проекция поверхности на ось
Случай неявного задания поверхности. ПлощадьПоверхности, заданной уравнениемВыражается интегралом
(19.22)
Где- проекция поверхности на плоскость
Случай параметрического задания поверхности. Если поверхность задана параметрическими уравнениями
Где- ограниченная замкнутая квадрируемая область, в которой
Функции х, у, z непрерывно дифференцируемы, то
(19.24)
Где
(19.25)
Пример 19.17. Найти площадь части поверхности цилиндра Заключенной внутри сферы(боковая поверх
Ность «тела Вивиани», рис. 19.19).
Применим формулу (19.20). Поскольку плоскостьюЦилиндр разделяется на две равные части, то можно вычислить половину искомой площади поверхности.
Вычислим площадь той части поверхности, уравнение которой Для определения области интегрирования следует спроецировать на плоскость линию пересечения поверхностей, уравнение которой находится исключениемИз данных уравнений. Вычитая одно уравнение из другого, получаемЭто
Так как
Уравнение параболы, лежащей в плоскости С вершиной на осиНа расстоянии от начала координат и пересекающей ось в точкахДуга указанной
Параболывместе с соответствующим отрезком осиСоставляют границу области.
Пример 19.18. Вычислить площадь поверхности конуса , заключенной внутри цилиндра Цилиндр отсекает на поверхности конуса две части, симметричные относительно плоскостиНа рис. 19.20 изображена только верхняя частьВычислим пло
ИшьЭтой части, проекция которой на плоскостьЕсть круг
Так как для рассматриваемой части конуса
То по формуле (19.19)
Получаем
Где- окружность Переходя к полярным координатам, находим
Следовательно, вся искомая площадь
Пример 19.
Цилиндр вырезает из сферы две части, верхняя из них изображена на рис. 19.21. Вычислим площадьПоверхности этой сферы. Для верхней полусферы
Следовательно,- круг
Переходя к полярным координатам, находим 338
Итак,
Рис. 19.20
Пример 19.20. Вычислить площадь частей сферы вырезанных из нее цилиндромВоспользовавшись параметрическими
Уравнениями сферической поверхности:
Рис. 19.21
Здесь вдет речь о вычислении площади верхнего и нижнего оснований «тела Вивиани» (см. рис. 19.19). Воспользуемся формулой (19.24), для чего предварительно найдем коэффициентыТак как
То по формулам (19.25)
НаходимСледовательно,
Ограничимся рассмотрением четверти изучаемой поверхности, лежащей в первом октанте. Для точек «кривой Вивиани», т. е. кривой пересечения сферы и цилиндра (в пределах первого октанта),Действительно подставляя выраженияИЧерезИВ уравнение цилиндраПолучаем И поскольку для рассматриваемых точек, очевидно, , то отсюда следует, что
Установив на основании сказанного пределы измененияИПо формуле (19.
| < Предыдущая | Следующая > |
|---|
Решение некоторых типовых задач, рассматриваемых в аудитории
|
Заглавная страница КАТЕГОРИИ: Археология Информатика ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 5 из 5 12.3.1. Вычислить площадь той части поверхности , которая находится над прямоугольником, лежащим в плоскости и ограниченным прямыми , , , . Решение. Найдем элемент площади поверхности: . Теперь легко найдем искомую площадь: . 12.3.2. Вычислить площадь части параболоида , вырезанной цилиндром . Решение. Поверхность задана уравнением , отсюда . Двойной интеграл, выражающий площадь, равен . Для его вычисления перейдем к полярным координатам: . 12.3.3. Вычислить часть поверхности конуса , отсекаемую цилиндром . Решение. В этом примере надо найти часть поверхности конуса, лежащую над кругом радиуса . Площадь круга равна . Вычислим элемент поверхности конуса: , . 12.3.4. Вычислить площадь части земной поверхности, считая ее сферой радиуса км, заключенной между меридианами , и параллелями и . Решение. Используя приведенную в пункте 12.1 формулу элемента площади в сферических координатах для сферы с уравнением , получим . Следует учесть, однако, (ср. замечание в пункте 11.1), что географическая широта и угол связаны соотношением , поэтому в нашем примере и . Отсюда км2. 12.3.5. Вычислить интеграл , где – полная поверхность конуса при . Решение. И боковая поверхность конуса, и его основание имеют одну и ту же проекцию на плоскость , а именно: круг радиуса , заданный неравенством . Поэтому будем вычислять поверхностный интеграл отдельно для основания и для боковой поверхности. На основании , поэтому интеграл равен . Для боковой поверхности элемент площади равен (см. пример 12.3.3). Функция интегрирования на боковой поверхности равна , отсюда поверхностный интеграл равен . Интеграл по всей поверхности получим сложением: . 12.3.6. Вычислить интеграл , где – поверхность тетраэдра , , , . Решение. Поверхность тетраэдра состоит из четырех граней, интеграл по каждой из которых будем вычислять отдельно. Грань, лежащая в плоскости , проектируется на плоскость в треугольник, ограниченный осями , и прямой . Уравнение поверхности этой грани , откуда . Таким образом, поверхностный интеграл по этой грани равен . Оставшиеся три грани расположены в координатных плоскостях. Для грани, расположенной в плоскости , , поэтому . Интегралы и по плоскостям и равны. Найдем, например . Здесь мы учли, что на плоскости и что . Теперь найдем окончательный ответ: . 12.3.7. Вычислить , где — часть плоскости , отсеченная координатными плоскостями. Решение. Из уравнения плоскости удобнее выразить , тогда элемент площади поверхности равен . Проекция поверхности на координатную плоскость является треугольником , ограниченным прямой и осями координат. Запишем соответствующий двойной интеграл: . 12. Решение. Очевидно, в силу симметричности координаты , и центра масс восьмой части сферы в указанной системе координат совпадают, поэтому найдем значение аппликаты. Воспользуемся выражением элемента площади сферы, вычисленным в пункте 12.1: . Здесь было учтено, что проекция восьмой части сферы на плоскость является четвертью круга и имеет площадь . Итак, центр масс находится в точке . 12.4. Задачи для самостоятельного решения ЧАСТЬ В) ДИСТАНЦИОННОЕ ОБУЧЕНИЕ 12.4.1. Найти площадь: а) части поверхности , вырезанной цилиндром и плоскостью ; б) части гиперболического параболоида , вырезанной цилиндром ; в) части , вырезанной поверхностью . 12.4.2. Найти центр масс части однородного параболоида , отсеченной плоскостью . 12.4.3. Вычислить поверхностный интеграл , где – часть плоскости , лежащая в первом октанте. 12.4.4. Вычислить , где – часть плоскости , лежащая в первом октанте. 12.4.5. Вычислить , где – полусфера . 12.4.6. Вычислить , где – цилиндр , ограниченный плоскостями и , а – расстояние от точки цилиндра до начала координат. 12.4.7. Вычислить , где – часть поверхности , отсеченная цилиндром , а – расстояние от точки поверхности до оси . 12.4.8. Найти массу сферы, если поверхностная плотность в каждой точке равна квадрату расстояния от этой точки до некоторого фиксированного диаметра сферы. Ответы. 12.4.1. а) ; б) ; в) . 12.4.2. . 12.4.3. . 12.4.4. . 12.4.5. . 12.4.6. .
⇐ Предыдущая12345 Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
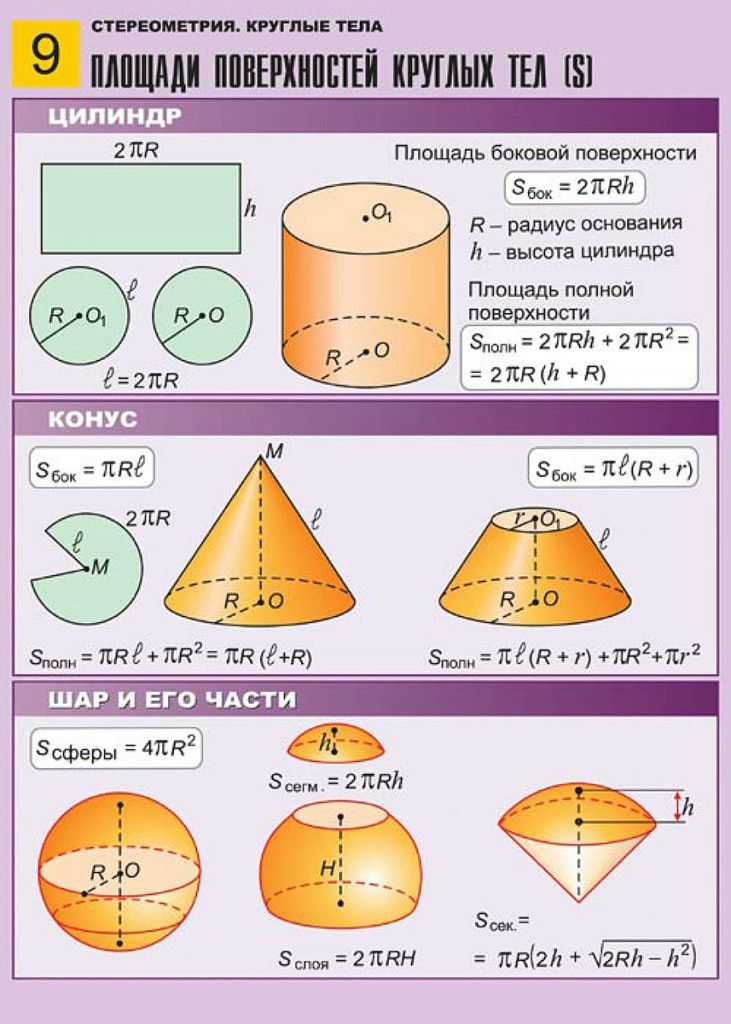
Площадь поверхности
Площадь поверхности
Определение площади поверхности
На первом курсе вычислений мы видели, как найти поверхность
площадь революции. Теперь, когда мы как
сила двойной интеграции, мы готовы взять на себя площадь поверхности для
более общие поверхности. Мы можем думать о гладкой поверхности как о одеяле.
хлопая на ветру. Он состоит из множества прямоугольников, залатанных
вместе. В более общем и более точном смысле пусть
z = f(x,y) — поверхность в R 3
определяется над областью R в плоскости xy. резать
плоскость xy на прямоугольники. Каждый прямоугольник будет проецироваться вертикально на
кусок поверхности, как показано на рисунке ниже.
прямоугольник в R равен
Площадь
= DyDx
Площадь соответствующего участка поверхности не будет DyDx
так как это не прямоугольник. Даже если мелко порежем, все равно не будем
создать прямоугольник, а скорее будет приблизительно производить
параллелограмм. Немного поэкспериментировав с геометрией, мы можем увидеть, что две соседние
стороны параллелограмма равны (в векторной форме)
и
= Dx i + f x (x,y)Dx
к
и
против
= f y (x,y)Dy i + Dy
к
Мы можем увидеть это, поняв, что частные производные — это наклоны в
каждое направление. Если мы запустим Dx
в направлении и , то мы будем
рост f x (x,y)Dx
в направлении k , так что
подъем/бег = f x (x,y)
Что согласуется с идеей наклона частной производной. Похожий
аргумент подтвердит уравнение для вектора v .
Теперь, когда мы знаем смежные векторы, вспомним, что площадь параллелограмма
является величиной векторного произведения двух соседних векторов. У нас есть
Это область одного из участков стеганого одеяла. Чтобы найти общее
площадь поверхности, складываем все площади и берем в качестве предела прямоугольник
размер приближается к нулю. Это приводит к двойной сумме Римана, т.
двойной интеграл. Приведем определение ниже.
Определение площади поверхности
Пусть г
= f(x,y) — дифференцируемая поверхность
определяется над областью R.
Тогда его площадь равна
Примеры
Пример
Найдите площадь поверхности части самолета
г
= 8x + 4y
, который находится внутри цилиндра
x 2
+ у 2 = 16
Раствор
Вычисляем частные производные
f x (x,y)
= 8 f y (x,y)
= 4
так что
1 + f x 2 (x,y)
+ ф у 2 (х, у) = 1 + 64 + 16 = 81
Извлекая квадратный корень и интегрируя, получаем
Мы
можно вычислить этот интеграл, но есть гораздо более простой способ.
константы — это просто константа, умноженная на площадь региона. Поскольку
регион это круг, получаем
Площадь поверхности = 9(16p)
= 144p
В
в действительности, поскольку в формуле есть квадратный корень, большая часть площади поверхности
расчеты требуют интенсивных навыков интеграции или использования машины.
Предыдущий пример и следующий пример не предназначены для обмана, а скорее для того, чтобы
показать, как сущность задач площади поверхности работает без интегрирования
затруднения, затуманивающие ваше понимание.
Пример
Найти
площадь поверхности части параболоида
г = 25 — х 2 — у 2
что
лежит выше плоскости xy.
Раствор
Вычисляем частные производные
f x (x,y)
= -2x f y (x,y)
= -2г
так что
1 + f x 2 (x,y)
+ f y 2 (x,y) = 1 + 4x 2 + 4y 2
В этот момент, если мы внимательно прислушаемся, мы услышим тихий умоляющий голос.
«Полярные координаты». Мы прислушиваемся к его зову и понимаем, что
регион это просто кружок
р
= 5
Теперь преобразуйте подынтегральную функцию в полярные координаты, чтобы получить
.
Сейчас
пусть
u = 1 + 4r 2
ду = 8rdr
и
заменить
Назад
на домашнюю страницу множественной интеграции
Назад
на домашнюю страницу векторного исчисления
Назад к математике
Домашняя страница отдела
электронная почта
Вопросы и предложения
многомерное исчисление — Площадь меньшей части поверхности
Задавать вопрос
спросил
6 лет, 3 месяца назад
Изменено
6 лет, 3 месяца назад
Просмотрено
169 раз
$begingroup$
9{2}}}drdtheta$$
(здесь $y_{x}$ обозначает производную от $y$ по $x$ и аналогично по $y_{z}$, и я использовал полярные координаты в плоскость $x,z$)
Этот интеграл кажется слишком сложным, что заставляет меня думать, что он либо неверен, либо есть более простой способ сделать это?
- многомерное исчисление
- поверхности
- поверхностные интегралы
$endgroup$
$begingroup$
Что-то у вас с интегралом.

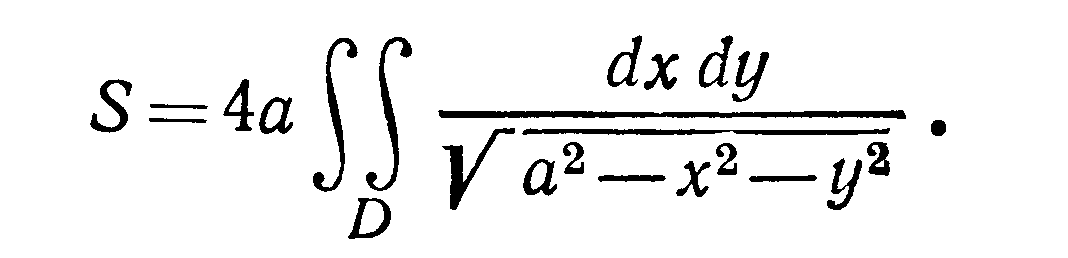
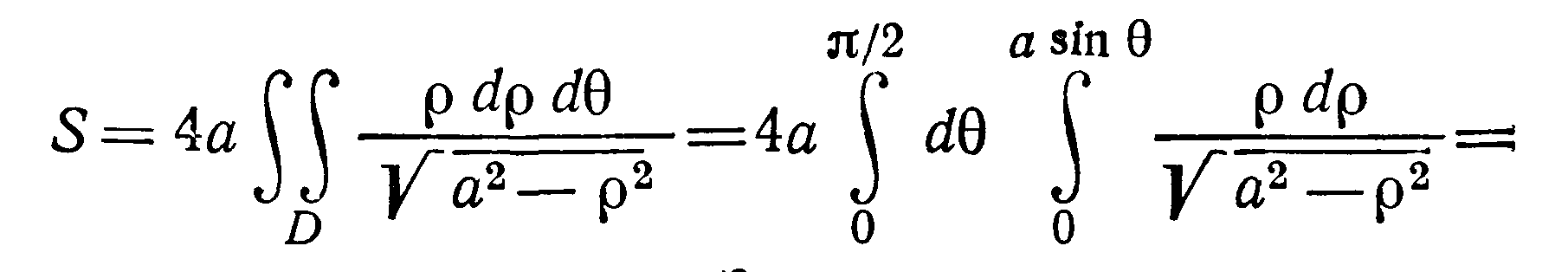


































 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
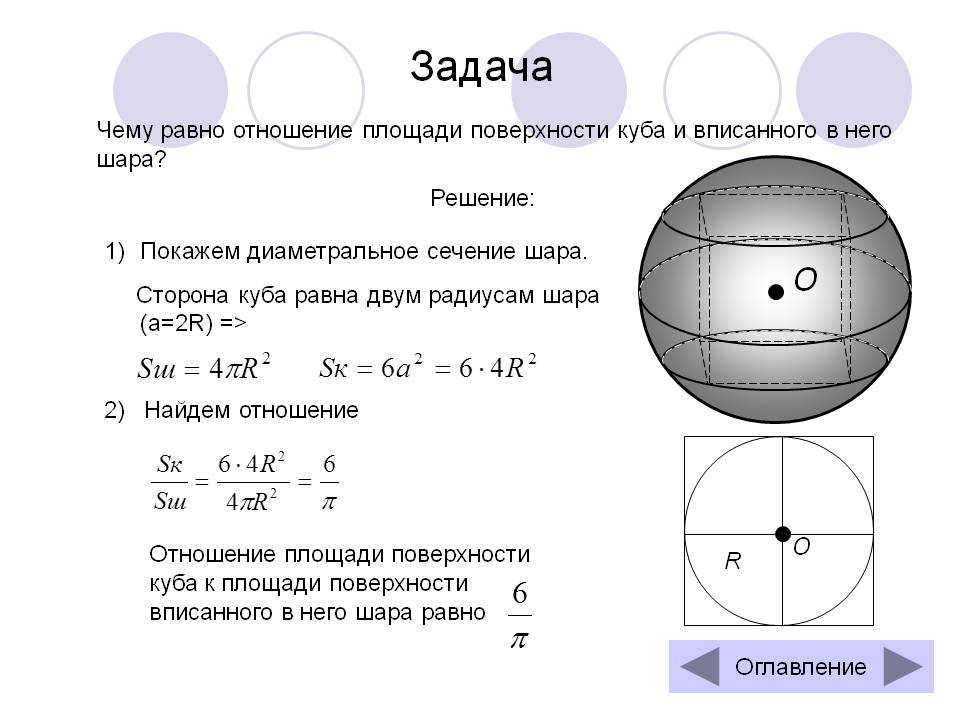
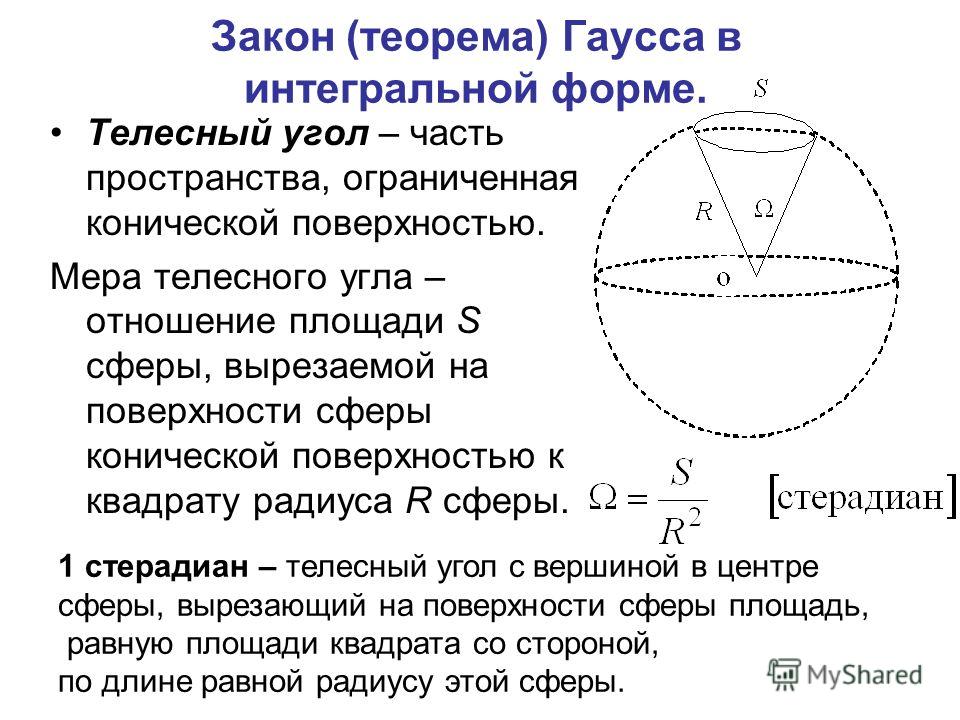
 3.8. Найти координаты центра масс восьмой части однородной сферы , , , .
3.8. Найти координаты центра масс восьмой части однородной сферы , , , .
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.012 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.012 с.) 

