Формулы объёма и площади поверхности. Многогранники.
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
 Куб |
|
|
 Параллелепипед |
|
|
 Прямоугольный параллелепипед |
|
|
 Призма |
|

|
 Пирамида |
|

|
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат),
(маленький прямоугольник),
Подставим все данные в формулу: 
Ответ: 424.
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник),
(маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно,
большая боковая грань призмы.
Поэтому или
откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда
(по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда
следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как
высота воды
должна быть в 81 раз меньше, чем
Она равна
(см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту
Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, 
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Загрузить PDF
Загрузить PDF
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру. Площадь поверхности является числовой характеристикой поверхности.[1]
Вычислить площадь поверхности объемной (трехмерной) фигуры довольно просто, если знать соответствующую формулу. Существует определенная формула для каждой фигуры, поэтому сначала нужно определить, какая фигура дана. Чтобы быстро вычислять площадь поверхности, запомните соответствующие формулы для разных фигур. В данной статье рассматриваются наиболее распространенные фигуры.
-
1
Запишите формулу для вычисления площади поверхности куба. У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a2, где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).[2]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте ребро куба. Ребра куба равны, поэтому можно измерить только одно (любое) ребро. Ребро измерьте с помощью линейки (или рулетки). Обратите внимание на используемые единицы измерения.
- Запишите значение, обозначив его через а.
- Например: а = 2 см
-
3
Значение а возведите в квадрат. То есть возведите в квадрат длину ребра куба. Для этого умножьте значение на себя. Если вы только приступили к изучению формул с квадратами, запишите формулу так: SA = 6*а*а.
- Сейчас вы вычислили значение площади одной из граней куба.
- Например: а = 2 см
- a2 = 2 х 2 = 4 см2
-
4
Вычисленное значение умножьте на шесть. Помните, что у куба шесть равных граней. Вычислив площадь одной из граней, умножьте полученное значение на 6, чтобы включить все грани куба.
- Это последний шаг в процессе вычисления площади поверхности куба.
- Например: а 2 = 4 см2
- SA = 6 х а2 = 6 х 4 = 24 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности прямоугольной призмы. У прямоугольной призмы шесть граней, причем равными являются только противоположные грани.[3]
Поэтому формула для вычисления площади поверхности прямоугольной призмы включает значения трех разных ребер: SA = 2ab + 2bc + 2ac.- Здесь а – ширина, b – высота, с – длина призмы.
- Если проанализировать формулу, можно понять, что она суммирует площади всех граней.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения высоты, ширины и длины призмы. Три ребра не являются равными, поэтому нужно выполнить три измерения. Измерьте соответствующие ребра с помощью линейки (или рулетки). Ребра измеряйте в одной единице измерения.
- Измерьте длину грани, которая лежит в основании призмы; длину обозначьте через с.
- Например: с = 5 см
- Измерьте ширину грани, которая лежит в основании призмы; ширину обозначьте через а.
- Например: а = 2 см
- Измерьте высоту призмы; высоту обозначьте через b.
- Например: b = 3 см
-
3
Вычислите площадь одной грани призмы, а затем полученное значение умножьте на два. Помните, что у прямоугольной призмы шесть граней, причем равными являются только противоположные грани. Умножьте длину на высоту (с на а), чтобы найти площадь одной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[4]
- Например: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 см2
-
4
Вычислите площадь другой грани призмы, а затем полученное значение умножьте на два. Умножьте ширину на высоту (а на b), чтобы найти площадь другой грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[5]
- Например: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 см2
-
5
Вычислите площадь фронтальной грани, а затем полученное значение умножьте на два. Умножьте длину на ширину (с на b), чтобы найти площадь фронтальной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[6]
- Например: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 см2
-
6
Сложите три значения. Так как площадь поверхности – это суммарная площадь всех граней фигуры, сложите найденные значения площадей отдельных граней. Вы получите площадь поверхности прямоугольной призмы.[7]
- Например: SA = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности треугольной призмы. Треугольная призма имеет две равные треугольные грани и три прямоугольные грани. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти площади всех граней и сложить их. Формула для вычисления площади поверхности треугольной призмы: SA = 2S + РH, где S – площадь треугольной грани, Р – периметр треугольной грани, H – высота призмы.[8]
- Здесь S – это площадь треугольника (треугольной грани), которая вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание).
- Р – периметр треугольника (треугольной грани), который равен сумме всех сторон треугольника.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Вычислите площадь треугольной грани и умножьте ее на два. Площадь треугольника вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание). Так как треугольная призма имеет две равные треугольные грани, эту формулу можно умножить на два. Поэтому, чтобы вычислить площади двух треугольных граней, просто перемножьте основание и высоту треугольника (b*h).[9]
- Основание треугольника b – это его нижняя сторона.
- Например: b = 4 см
- Высота треугольника h – это перпендикуляр, опущенный на основание из противоположной вершины.
- Например: h = 3 см
- Площадь двух треугольных граней равна: 2(1/2)b*h = b*h = 4*3 =12 см.
-
3
Измерьте каждую сторону треугольника и высоту призмы. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти значение каждой стороны треугольника и высоты призмы. Высота призмы – это расстояние между треугольными гранями.
- Например: Н = 5 см
- Стороны треугольника – это три ребра одной (любой) из треугольных граней.
- Например: а = 2 см, b = 4 см, с = 6 см
-
4
Вычислите периметр треугольника. Для этого сложите все стороны треугольника: Р = а + b + с.
- Например: P = а + b + с = 2 + 4 + 6 = 12 см
-
5
Перемножьте периметр треугольной грани и высоту призмы. Помните, что высота призмы – это расстояние между треугольными гранями. Таким образом, Р умножьте на Н.
- Например: Р х Н = 12 х 5 = 60 см2
-
6
Сложите полученные значения. Чтобы найти площадь поверхности треугольной призмы, сложите два значения, вычисленные ранее.[10]
- Например: 2S + PH = 12 + 60 = 72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности шара. Шар имеет изогнутую поверхность, поэтому формула включает математическую константу π (число Пи). Чтобы вычислить площадь поверхности шара, воспользуйтесь формулой SA = 4π*r2.[11]
- Здесь r – радиус шара, π ≈ 3,14.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус шара. Радиус шара равен половине его диаметра, то есть половине отрезка, который проходит через центр шара и соединяет две точки, лежащие на его поверхности.[12]
- Например: r = 3 см
-
3
Радиус шара возведите в квадрат. Для этого умножьте значение радиуса (r) на себя. Помните, что формулу можно записать так: SA = 4π*r*r.[13]
- Например: r2 = r x r = 3 x 3 = 9 см2
-
4
Перемножьте квадрат радиуса и приблизительное значение числа Пи. Число Пи является математической константой, которая равна отношению длины окружности к ее диаметру.[14]
Это иррациональное число со множеством цифр после десятичной запятой. Зачастую число Пи округляется до 3,14. Квадрат радиуса умножьте на π (на 3,14), чтобы вычислить площадь круглого сечения шара. [15]
- Например: π*r2 = 3,14 x 9 = 28,26 см2
-
5
Полученное значение умножьте на четыре. Чтобы найти значение площади поверхности сферы, площадь круглого сечения умножьте на 4.[16]
- Например: 4π*r2 = 4 x 28,26 = 113,04 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности цилиндра. Цилиндрическая поверхность этой фигуры ограничена двумя круглыми параллельными плоскостями, которые называются основаниями. Формула для вычисления площади поверхности цилиндра: SA = 2π*r2 + 2π*rh, где r – радиус основания, h – высота цилиндра, π ≈ 3,14.[17]
- 2π*г2 – это площадь двух оснований, а 2πrh – это площадь цилиндрической поверхности.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту цилиндра. Радиус окружности равен половине ее диаметра, то есть половине отрезка, который проходит через центр окружности и соединяет две точки, лежащие на ней.[18]
Высота цилиндра – это расстояние между его основаниями. Измерьте и запишите радиус основания и высоту цилиндра.- Например: r = 3 см
- Например: h = 5 см
-
3
Вычислите площадь основания и умножьте ее на два. Чтобы найти площадь основания, воспользуйтесь формулой для вычисления площади круга: S = π*г2. Сначала радиус возведите в квадрат, а затем полученное значение умножьте на число Пи. Результат умножьте на два, чтобы учесть второе равное основание.[19]
- Например: площадь основания = π*r2 = 3,14 х 3 х 3 = 28,26 см2
- Например: 2π*r2 = 2 x 28,26 = 56,52 см2
-
4
Вычислите площадь цилиндрической поверхности. Для этого воспользуйтесь формулой S = 2π*rh, по которой можно найти площадь поверхности трубы. Здесь труба – это поверхность между двумя основаниями цилиндра. Перемножьте двойку, число Пи, радиус и высоту.[20]
- Например: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 см2
-
5
Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.[21]
- Например: 2π*r2 + 2π*rh = 56,52 + 94,2 = 150,72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности квадратной пирамиды. Квадратная пирамида имеет одно квадратное основание и четыре треугольные грани. Помните, что площадь квадрата равна квадрату его стороны. Площадь треугольника равна 1/2sl (половина основания треугольника, умноженная на его высоту). Так как пирамида имеет четыре треугольные грани, нужно площадь треугольника умножить на 4. Таким образом, площадь поверхности квадратной пирамиды вычисляется по формуле: SA = s2 + 2sl.[22]
- В этой формуле s – ребро квадратной грани (сторона квадрата), l – апофема пирамиды.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения апофемы и ребра квадратной грани. Апофема (l) – это высота треугольной грани, то есть расстояние между основанием треугольника и его вершиной. Ребро квадратной грани (s) – это сторона квадрата. Помните, что у квадрата все стороны равны, поэтому измерьте любое ребро квадратной грани, а также измерьте апофему пирамиды.[23]
- Например: l = 3 см
- Например: s = 1 см
-
3
Найдите площадь квадратной грани. Для этого возведите в квадрат ребро этой грани (сторону квадрата), то есть умножьте значение s на себя.[24]
- Например: s2 = s х s = 1 х 1 = 1 см2
-
4
Вычислите общую площадь четырех треугольных граней. Вторая часть формулы включает суммарную площадь четырех треугольных граней. Согласно формуле 2ls, перемножьте 2, s и l. Так вы найдете суммарную площадь 4-х треугольных граней.[25]
- Например: 2 х s х l = 2 х 1 х 3 = 6 см2
-
5
Сложите полученные значения. Сложите площадь квадратной грани и общую площадь четырех треугольных граней, чтобы вычислить площадь поверхности пирамиды.[26]
- Например: s2 + 2sl = 1 + 6 = 7 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности конуса. Конус имеет круглое основание и закругленную боковую поверхность, которая сужается в вершине этой фигуры. Чтобы найти площадь поверхности конуса, нужно вычислить значения площади круглого основания и площади боковой поверхности, а затем сложить эти значения. Формула для вычисления площади поверхности конуса: SA = π*r2 + π*rl, где r – радиус круглого основания, l – образующая (расстояние между вершиной конуса и точкой, которая лежит на окружности круга), π ≈ 3,14.[27]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту конуса. Радиус – это отрезок, соединяющий центр круга и точку, которая лежит на его окружности. Высота – это расстояние между центром круга и высотой конуса.[28]
- Например: r = 2 см
- Например: h = 4 см
-
3
Найдите значение образующей конуса (l). Образующая конуса является гипотенузой треугольника, поэтому воспользуйтесь теоремой Пифагора, чтобы вычислить образующую: l = √(r2 + h2), где r – радиус круглого основания, h – высота конуса.[29]
- Например: l = √(r2 + h2) = √(2 х 2 + 4 х 4) = √(4 + 16) = √(20) = 4,47 см
-
4
Вычислите площадь круглого основания. Площадь круга вычисляется по формуле S = π*r2. Измерив радиус, возведите его в квадрат (умножьте r на себя), а затем квадрат радиуса умножьте на число Пи.[30]
- Например: π*r2 = 3,14 x 2 x 2 = 12,56 см2
-
5
Вычислите площадь боковой поверхности конуса. Сделайте это по формуле S = π*rl, где r – радиус круга, l – образующая, которая найдена ранее.[31]
- Например: π*rl = 3,14 x 2 x 4,47 = 28,07 см
-
6
Сложите полученные значения, чтобы найти площадь поверхности конуса. Площадь поверхности конуса равна сумме площади круглого основания и площади боковой поверхности конуса.[32]
- Например: π*r2 + π*rl = 12,56 + 28,07 = 40,63 см2
Реклама
Что вам понадобится
- Линейка
- Ручка или карандаш
- Бумага
Об этой статье
Эту страницу просматривали 70 137 раз.
Была ли эта статья полезной?
[{Large{text{Основные факты о площади}}}]
Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной (1) см, (1) мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см(^2), мм(^2) соответственно.
Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.
Свойства площади
1. Площадь любого многоугольника — величина положительная.
2. Равные многоугольники имеют равные площади.
3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
4. Площадь квадрата со стороной (a) равна (a^2).
[{Large{text{Площадь прямоугольника и параллелограмма}}}]
Теорема: площадь прямоугольника
Площадь прямоугольника со сторонами (a) и (b) равна (S=ab).
Доказательство
Достроим прямоугольник (ABCD) до квадрата со стороной (a+b), как показано на рисунке:
Данный квадрат состоит из прямоугольника (ABCD), еще одного равного ему прямоугольника и двух квадратов со сторонами (a) и (b). Таким образом,
(begin{multline*} S_{a+b}=2S_{text{пр-к}}+S_a+S_b Leftrightarrow
(a+b)^2=2S_{text{пр-к}}+a^2+b^2 Leftrightarrow\
a^2+2ab+b^2=2S_{text{пр-к}}+a^2+b^2 Rightarrow
S_{text{пр-к}}=ab end{multline*})
Определение
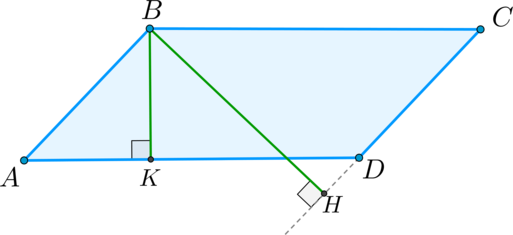
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота (BK) падает на сторону (AD), а высота (BH) — на продолжение стороны (CD):
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры (AB’) и (DC’), как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма (ABCD).
Тогда (AB’C’D) – прямоугольник, следовательно, (S_{AB’C’D}=AB’cdot
AD).
Заметим, что прямоугольные треугольники (ABB’) и (DCC’) равны. Таким образом,
(S_{ABCD}=S_{ABC’D}+S_{DCC’}=S_{ABC’D}+S_{ABB’}=S_{AB’C’D}=AB’cdot
AD.)
[{Large{text{Площадь треугольника}}}]
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
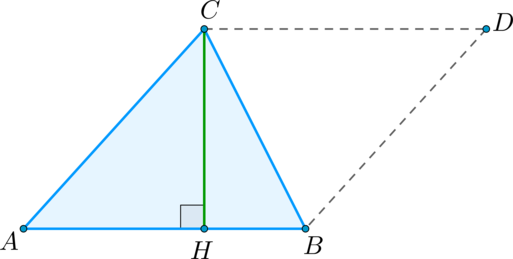
Пусть (S) – площадь треугольника (ABC). Примем сторону (AB) за основание треугольника и проведём высоту (CH). Докажем, что [S = dfrac{1}{2}ABcdot CH.] Достроим треугольник (ABC) до параллелограмма (ABDC) так, как показано на рисунке:
Треугольники (ABC) и (DCB) равны по трем сторонам ((BC) – их общая сторона, (AB = CD) и (AC = BD) как противоположные стороны параллелограмма (ABDC)), поэтому их площади равны. Следовательно, площадь (S) треугольника (ABC) равна половине площади параллелограмма (ABDC), то есть (S = dfrac{1}{2}ABcdot CH).
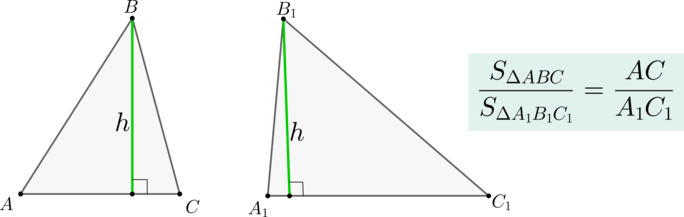
Теорема
Если два треугольника (triangle ABC) и (triangle A_1B_1C_1) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
Теорема
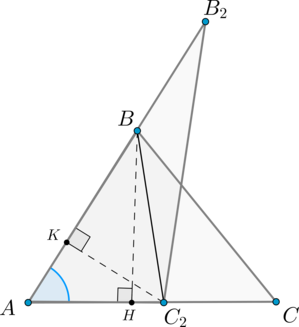
Если два треугольника (triangle ABC) и (triangle A_2B_2C_2) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть (angle A=angle A_2). Совместим эти углы так, как показано на рисунке (точка (A) совместилась с точкой (A_2)):
Проведем высоты (BH) и (C_2K).
Треугольники (AB_2C_2) и (ABC_2) имеют одинаковую высоту (C_2K), следовательно: [dfrac{S_{AB_2C_2}}{S_{ABC_2}}=dfrac{AB_2}{AB}]
Треугольники (ABC_2) и (ABC) имеют одинаковую высоту (BH), следовательно: [dfrac{S_{ABC_2}}{S_{ABC}}=dfrac{AC_2}{AC}]
Перемножая последние два равенства, получим: [dfrac{S_{AB_2C_2}}{S_{ABC}}=dfrac{AB_2cdot AC_2}{ABcdot AC} qquad text{ или
} qquad dfrac{S_{A_2B_2C_2}}{S_{ABC}}=dfrac{A_2B_2cdot
A_2C_2}{ABcdot AC}]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть (p) – полупериметр треугольника, (a), (b), (c) – длины его сторон, тогда его площадь равна [S_{triangle}=sqrt{p(p — a)(p —
b)(p — c)}]
[{Large{text{Площадь ромба и трапеции}}}]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
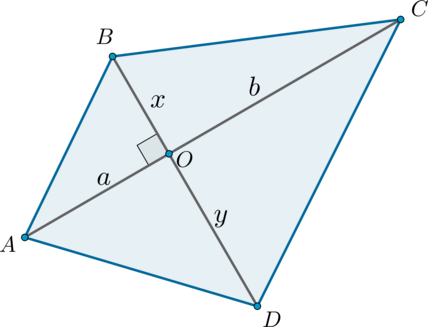
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник (ABCD). Обозначим (AO=a, CO=b, BO=x,
DO=y):
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
(begin{multline*}
S_{ABCD}=frac12ax+frac12xb+frac12by+frac12ay=frac12(ax+xb+by+ay)=\
frac12((a+b)x+(a+b)y)=frac12(a+b)(x+y)end{multline*})
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: [S_{text{ромб}}=dfrac12 d_1cdot d_2]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
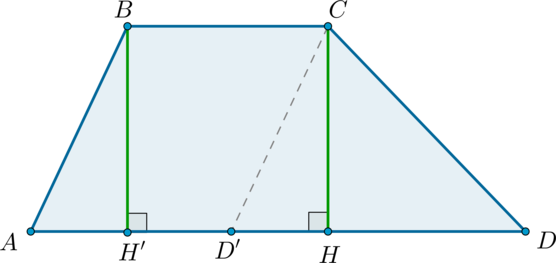
Доказательство
Рассмотрим трапецию (ABCD) с основаниями (BC) и (AD). Проведем (CD’parallel AB), как показано на рисунке:
Тогда (ABCD’) – параллелограмм.
Проведем также (BH’perp AD, CHperp AD) ((BH’=CH) – высоты трапеции).
Тогда (S_{ABCD’}=BH’cdot AD’=BH’cdot BC, quad S_{CDD’}=dfrac12CHcdot D’D)
Т.к. трапеция состоит из параллелограмма (ABCD’) и треугольника (CDD’), то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
[S_{ABCD}=S_{ABCD’}+S_{CDD’}=BH’cdot BC+dfrac12CHcdot
D’D=dfrac12CHleft(2BC+D’Dright)=] [=dfrac12
CHleft(BC+AD’+D’Dright)=dfrac12 CHleft(BC+ADright)]
Многоугольником считается фигура,имеющая количество сторон больше или равное 3.
1)Площадь треугольника со сторонами a,b,c, и высотами h1,h2,h3,
площадь S =a*h1/2=b*h2/2=c*h3/2,
или по формуле Герона :
S= V p*(p-a)*(p-b)*(p-c),
где p — полупериметр.
Площадь четырехугольника:
1)площадь квадрата :S = a^2,
2)площадь прямоугольника :S = a *b,
3)площадь параллелограмма : S =a * h1 = b *h2,
4)площадь ромба S = a *h =d1*d2,
где a,b -стороны четырёхугольника,h1,h2-высоты,d1,d2-диагонали ромба.
5)площадь произвольного четырёхугольника определяется путем разбивки его по диагонали и нахождения площади каждого треугольника отдельно.
Площадь правильного многоугольника равна произведению полупериметра =n*a,на апофему h
S=(n*a)*h/2
где а-сторона многоугольника,n-число сторон,h-апофема.
Download Article
Download Article
Calculating the area of a polygon can be as simple as finding the area of a regular triangle or as complicated as finding the area of an irregular eleven-sided shape. If you want to know how to find the area of a variety of polygons, just follow these steps.
Area Help
-
1
Write down the formula for finding the area of a regular polygon. To find the area of a regular polygon, all you have to do is follow this simple formula: area = 1/2 x perimeter x apothem.[1]
Here is what it means:-
Perimeter = the sum of the lengths of all the sides[2]
- Apothem = a segment that joins the polygon’s center to the midpoint of any side that is perpendicular to that side[3]
-
Perimeter = the sum of the lengths of all the sides[2]
-
2
Find the apothem of the polygon. If you’re using the apothem method, then the apothem will be provided for you. Let’s say you’re working with a hexagon that has an apothem with a length of 10√3.
Advertisement
-
3
Find the perimeter of the polygon. If the perimeter is provided for you, then you’re nearly done, but it’s likely that you have a bit more work to do. If the apothem is provided for you and you know that you’re working with a regular polygon, then you can use it to find the perimeter. Here’s how you do it:[4]
- Think of the apothem as being the «x√3» side of a 30-60-90 triangle. You can think of it this way because the hexagon is made up of six equilateral triangles. The apothem cuts one of them in half, creating a triangle with 30-60-90 degree angles.
- You know that the side across from the 60 degree angle has length = x√3, the side across from the 30 degree angle has length = x, and the side across from the 90 degree angle has length = 2x. If 10√3 represents «x√3,» then you can see that x = 10.
- You know that x = half the length of the bottom side of the triangle. Double it to get the full length. The bottom side of the triangle is 20 units long. There are six of these sides to the hexagon, so multiply 20 x 6 to get 120, the perimeter of the hexagon.
-
4
Plug the apothem and the perimeter into the formula. If you’re using the formula area = 1/2 x perimeter x apothem, then you can plug in 120 for the perimeter and 10√3 for the apothem. Here is what it will look like:[5]
- area = 1/2 x 120 x 10√3
- area = 60 x 10√3
- area = 600√3
-
5
Simplify your answer. You may need to state your answer in decimal instead of square root form. Just use your calculator to find the closest value for √3 and multiply it by 600. √3 x 600 = 1,039.2. This is your final answer.[6]
Advertisement
-
1
Find the area of a regular triangle. If you want to find the area of a regular triangle, all you have to do is follow this formula: area = 1/2 x base x height.
- If you have a triangle with a base of 10 and a height of 8, then the area = 1/2 x 8 x 10, or 40.
-
2
Find the area of a square. To find the area of a square, just square the length of one side. This is really the same thing as multiplying the base of the square by its height, because the base and height are the same.
- If the square has a side length of 6, then the area is 6 x 6, or 36.
-
3
Find the area of a rectangle. To find the area of a rectangle, simply multiply the base times the height.
- If the base of the rectangle is 4 and the height is 3, then the area of the rectangle is 4 x 3, or 12.
-
4
Find the area of a trapezoid. The find the area of a trapezoid, you just have to follow this formula: area = [(base 1 + base 2) x height]/2.
- Let’s say you have a trapezoid with bases that have a length of 6 and 8 and a height of 10. The area is simple [(6 +
x 10]/2, which can be simplified to (14 x 10)/2, or 140/2, which makes for an area of 70.
- Let’s say you have a trapezoid with bases that have a length of 6 and 8 and a height of 10. The area is simple [(6 +
Advertisement
-
1
Write down the coordinates of the vertices[7]
of the irregular polygon. Determining the area for an irregular polygon can be found when you know the coordinates of the vertices.[8]
-
2
Create an array. List the x and y coordinates of each vertex of the polygon in counterclockwise order. Repeat the coordinates of the first point at the bottom of the list.[9]
-
3
Multiply the x coordinate of each vertex by the y coordinate of the next vertex. Add the results. The added sum of these products is 82.
-
4
Multiply the y coordinate of each vertex by the x coordinate of the next vertex. Again, add these results. The added total of these products is -38.
-
5
Subtract the sum of the second products from the sum of the first products. Subtract -38 from 82 to get 82 — (-38) = 120.
-
6
Divide this difference by 2 to get the area of the polygon. Just divide 120 by 2 to get 60 and you’re all done.
Advertisement
Add New Question
-
Question
How can I calculate the area of an irregular polygon?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
Divide the polygon into several triangles. Then, calculate the area of each triangle by multiplying the base by half of the height. Add the different areas together to find the total area of the polygon.
-
Question
How do I calculate the area of an octagon?
Cut it into smaller shapes, such as triangles or other quadrilaterals using angles. Find the area of each smaller shape, then add the areas together to find the area of the whole shape.
-
Question
How do I find the area of a 4-sided shape?
Assuming it’s not a square or rectangle, you would have to subdivide the figure into smaller sections consisting of squares, rectangles, triangles, and other shapes whose areas can be easily calculated. Then add those areas together.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
If you list the points in a clockwise order instead of counterclockwise, you will get the negative of the area. Hence this can be used as a tool to identify the cyclic path or sequence of a given set of points forming a polygon.
-
This formula computes area with orientation. If you use it on a shape where two of the lines cross like a figure eight, you will get the area surrounded counterclockwise minus the area surrounded clockwise.
Advertisement
References
About This Article
Article SummaryX
A polygon is any kind of closed, 2-dimensional shape with at least 3 straight sides and no curves. If a polygon is regular—that is, all of its sides are the same length—you can easily find the area given the side length and the apothem. The apothem is the distance from the exact center of the polygon to the center of any of the sides. If you know the apothem and the side length, simply use the formula area = ½ x perimeter x apothem. You can find the perimeter by adding together the lengths of all the sides, or multiplying the length of a side by the number of sides. For example, say you have a hexagon with an apothem that has a length of 3 units, and each side has a length of 7 units. Multiply 7 by 6 (the number of sides in the hexagon) to find the perimeter of 42 units. Multiply 42 x 3 x ½ to get an area of 63 square units. Some types of polygons have their own special formulas that you can use to find the area. For instance, to calculate the area of a triangle, use the formula ½ x base x height. For a rectangle, all you need to do is multiply length times width. Since the length and width are the same for a square, simply square the length of one of the sides to calculate the area. If your shape is a trapezoid, add together the lengths of the two parallel sides, then multiply the sum by the height of the trapezoid. Divide the result by 2 to get the area. In other words, use the formula area = (base1 + base2) x h x ½. When you’re dealing with an irregular polygon, things get a little trickier. The easiest way to find the area of an irregular polygon is to plot it on a graph and find the coordinates of each of the vertices, or corners. Create a table with the x-coordinate of each vertex in one column, and the y-coordinate of each vertex in the next column. Multiply the x-coordinate of each vertex by the y-coordinate of the vertex below it in the table and add all the products together. Then go back the other way, and multiply each y-coordinate by the x-coordinate below it. Add together those products as well. Subtract the sum of the second set of products from the sum of the first set, then divide the difference by 2 to find the area of the polygon. If you need to calculate the area of an irregularly-shaped polygon, keep reading to learn how!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,468,327 times.
Reader Success Stories
-
Olexiy Korshunov
Aug 14, 2019
«The calculation of the area of an irregular polygons is very intelligibly written and is easily implemented for…» more
































































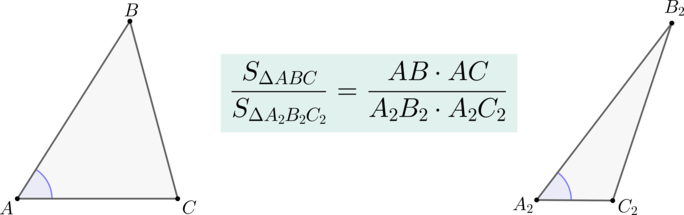










 x 10]/2, which can be simplified to (14 x 10)/2, or 140/2, which makes for an area of 70.
x 10]/2, which can be simplified to (14 x 10)/2, or 140/2, which makes for an area of 70.





