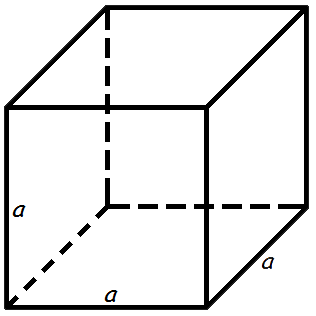
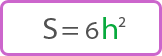Как найти площадь поверхности куба фигур - Avtoru.top

Определение куба

Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.

Онлайн-калькулятор площади поверхности куба

У куба есть двенадцать ребер, то есть, отрезков, которые являются сторонами квадратов.
Также он имеет восемь вершин и шесть граней.
У куба есть диагональ, соединяющая противоположные вершины.

Формула площади поверхности куба

Площадь поверхности куба – это сумма площадей всех его граней:

S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6

Площадь каждой грани одинакова, то есть:

S1=S2=S3=S4=S5=S6=S′S_1=S_2=S_3=S_4=S_5=S_6=S’

S′S’ — площадь любой грани куба.

Тогда полная площадь поверхности куба запишется как:

S=6⋅S′S=6cdot S’

Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.

Формула площади поверхности куба по длине ребра куба

Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:

S′=a⋅a=a2S’=acdot a=a^2

aa — сторона куба.

Отсюда, окончательно площадь поверхности куба:

S=6⋅a2S=6cdot a^2

aa — длина стороны куба.

Пример

Найти площадь поверхности куба, если длина его ребра равна 12 (см.).

Решение

a=12a=12

S=6⋅a2=6⋅122=6⋅144=864S=6cdot a^2=6cdot 12^2=6cdot 144=864 (см. кв.)

Ответ: 864 см. кв.

Формула площади поверхности куба по диагонали куба

По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:

d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
d=3⋅ad=sqrt{3}cdot a

Отсюда:

a=d3a=frac{d}{sqrt{3}}

Подставим в формулу для площади:

S=6⋅a2=6⋅(d3)2=2⋅d2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2

S=2⋅d2S=2cdot d^2

dd — диагональ куба.

Пример

Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.

Решение

14⋅d=2frac{1}{4}cdot d=2

Найдем диагональ:

d=4⋅2=8d=4cdot 2=8

Площадь:

S=2⋅d2=2⋅82=2⋅64=128S=2cdot d^2=2cdot 8^2=2cdot 64=128 (см. кв.)

Ответ: 128 см. кв.

Формула площади поверхности куба по длине диагонали квадрата (грани куба)

По теореме Пифагора, диагональ квадрата ll связанна с его стороной aa:

l2=a2+a2l^2=a^2+a^2
l2=2⋅a2l^2=2cdot a^2
l=2⋅al=sqrt{2}cdot a

Тогда сторона квадрата:

a=l2a=frac{l}{sqrt{2}}

Подставляем в формулу для площади и получаем:

S=6⋅a2=3⋅l2S=6cdot a^2=3cdot l^2

S=3⋅l2S=3cdot l^2

ll — диагональ квадрата (грани куба).

Пример

Одна четвертая часть диагонали квадрата равна 1 (см). Найти площадь поверхности куба, образованного данным четырехугольником.

Решение

14⋅l=1frac{1}{4}cdot l=1

Найдем диагональ квадрата:

l=4⋅1=4l=4cdot 1=4

Тогда площадь:

S=3⋅l2=3⋅42=48S=3cdot l^2=3cdot 4^2=48 (см. кв.)

Ответ: 48 см. кв.

Разберем более сложные примеры.

Формула площади поверхности куба по площади вписанного в куб шара

В куб вписан шар площади SшарS_{text{шар}}. Тогда радиус RR этого шара равен половине длины стороны куба aa:

R=a2R=frac{a}{2}

Площадь шара дается формулой:

Sшар=4⋅π⋅R2S_{text{шар}}=4cdotpicdot R^2

Отсюда найдем радиус шара:

R=Sшар4⋅πR=sqrt{frac{S_{text{шар}}}{4cdotpi}}

Сторона грани куба:

a=2⋅R=2⋅Sшар4⋅πa=2cdot R=2cdotsqrt{frac{S_{text{шар}}}{4cdotpi}}

Наконец площадь поверхности куба:

S=6⋅a2=6⋅SшарπS=6cdot a^2=frac{6cdot S_{text{шар}}}{pi}

S=6⋅SшарπS=frac{6cdot S_{text{шар}}}{pi}

SшарS_{text{шар}} — площадь шара, вписанного в куб.

Пример

В куб вписан шар, площадь которого равна 64 “пи” (см. кв.). Найти полную площадь поверхности куба.

Решение

Sшар=64πS_{text{шар}}=64pi

По формуле:

S=6⋅Sшарπ=6⋅64⋅ππ=384S=frac{6cdot S_{text{шар}}}{pi}=frac{6cdot 64cdotpi}{pi}=384 (см. кв.)

Ответ: 384 см. кв.

Не знаете, кто сможет решить контрольную работу на заказ для вас? Наши эксперты с удовольствием окажут вам помощь!

Тест по теме “Площадь поверхности куба”

Источник

В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.

Формула вычисления площади куба
- 1. Через длину ребра
- 2. Через длину диагонали грани
Примеры задач

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.

S = 6 ⋅ a²

Данная формула получена следующим образом:

Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
Площадь каждой грани считается так: S = a ⋅ a = a².
Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a².

2. Через длину диагонали грани

Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.

Это значит, что вычислить площадь поверхности фигуры можно так:

S = 6 ⋅ (d/√2)²

Примеры задач

Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.

Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)² = 864 см².

Задание 2
Площадь поверхности куба равняется 294 см². Вычислите длину его ребра.

Решение:
Примем ребро куба за a. Из формулы расчета площади следует:

Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.

Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)² = 75 см².

Источник

Формулы площади поверхности геометрических фигур

Площадь геометрической фигуры

— численная характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Площадь куба

Куб

Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.

Формула площади куба:

S = 6 a²

где S — площадь куба,

a — длина грани куба.

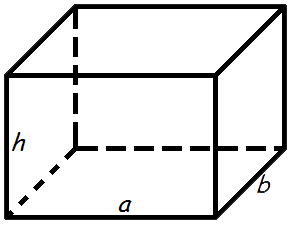
Площадь прямоугольного параллелепипеда

Формула площади поверхности прямоугольного параллелепипеда:

S = 2(a · b + a · h + b · h)

где S — площадь прямоугольного параллелепипеда,

a — длина,

b — ширина,

h — высота.

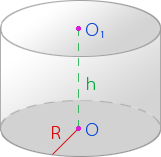
Площадь цилиндра

Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.

Формула для вычисления площади боковой поверхности цилиндра:

S = 2 π R h

Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.

Формула для вычисления площади полной поверхности цилиндра:

S = 2 π R h + 2 π R ² = 2 π R(R + h)

где S — площадь,

R — радиус цилиндра,

h — высота цилиндра,

π = 3.141592.

Площадь конуса

Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π.

Формула площади боковой поверхности конуса:

S = π R l

Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.

Формула площади полной поверхности конуса:

S = π R² + π R l = π R (R + l)

где S — площадь,

R — радиус основания конуса,

l — образующая конуса,

π = 3.141592.

Площадь шара

Формулы площади шара:

шар

Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число π.

S = 4 π R²
Площадь поверхности шара равна квадрату его диаметра умноженного на число π.

S = π D²

где S — площадь шара,

R — радиус шара,

D — диаметр шара,

π = 3.141592.

Источник

Перейти к содержанию

Площадь поверхности куба

На чтение 1 мин

Куб – это объемное тело ограниченное кубической поверхностью, которая состоит из шести равных и попарно параллельных квадратов.

h – ребро куба

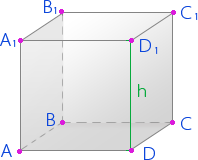
A,B,C,D,A₁,B₁,C₁,D₁ – вершины куба

Площадь поверхности куба – это суммарная площадь всех шести граней куба.

Площадь поверхности куба (S) определяется по формуле:

Вам также может понравиться

Цилиндр – это объемное тело, ограниченное цилиндрической

0156

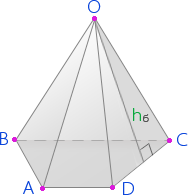
Пирамида – это объемное тело, ограниченное пирамидальной

0109

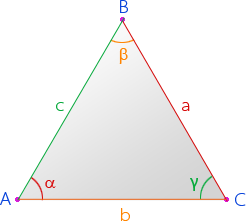
Рассмотрим прямоугольный треугольник АВС.

0116

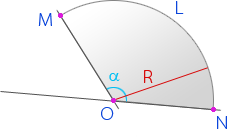
Дуга – это часть окружности, отсекаемая хордой.

0156

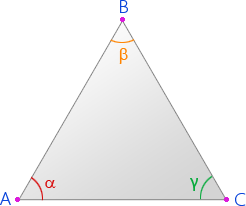
Рассмотрим произвольный треугольник АВС. α, β, γ –

01.5к.

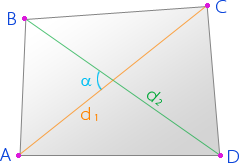
Четырехугольник – это многоугольник, имеющий четыре

094

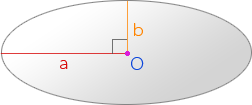
Эллипс – это множество точек плоскости, для которых

03.2к.

Прямоугольник – это параллелограмм, у которого все

062

Источник

Загрузить PDF

Площадь куба — это сумма площади всех его сторон. Все стороны куба равны, поэтому, чтобы найти площадь куба, надо найти площадь одной из его сторон и умножить на 6. Мы расскажем, как это делается.

1

Площадь куба — это сумма площади всех шести его сторон. Вот формула: 6 x s², где «s» — это сторона куба.^[1]
2

Найдите площадь одной из сторон куба, то есть «s», длину стороны куба, а затем нужно найти s². То есть, длина стороны куба в квадрате — это площадь, поскольку длина и ширина равны между собой. Если одна сторона куба, «s», равна 4 см, тогда площадь стороны куба равна (4 см)², то есть 16 см². Площадь всегда записывается в квадратных сантиметрах.^[2]
3

Умножьте площадь стороны куба на 6. 16 см² x 6 = 96 см². Площадь куба равна 96 см².^[3]

Реклама

1

Найдите объем куба. Например, объем куба 125 см³.^[4]
2

Найдите корень кубический объема куба. В нашем случае кубический корень числа 125 это 5, потому что 5 x 5 x 5 = 125. В нашем случае «s», то есть одна сторона куба равна 5.^[5]
3

Подставьте этот результат в формулу площади куба: 6 x s². Длина одной стороны куба 5 см, значит: 6 x (5 см)².
4

Решите пример. 6 x (5 см)² = 6 x 25 см² = 150 см ².

Реклама