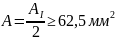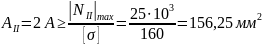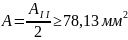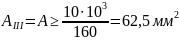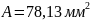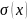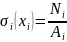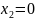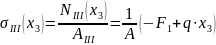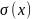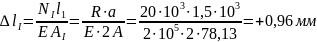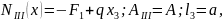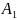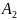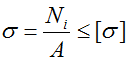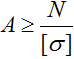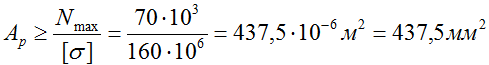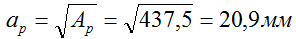Как найти площадь поперечного сечения стержня - Avtoru.top

Поскольку
площади поперечных сечений стержня на
разных его участках различны, найдем
минимально необходимое значение

из условия прочности каждого из участков.

1. На первом
участке

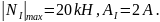
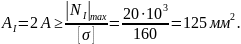
Отсюда получим

2. На втором участке

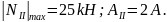
Отсюда следует,
что

.

3. На
третьем участке

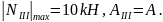
Из полученных
значений A
выбираем наибольшее, т.е. принимаем

В итоге получим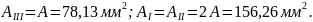

4. Построение эпюры нормальных напряжений

Построим эпюру
нормальных напряжений (т.е. график

),
которая позволит проверить правильность
подбора площадей поперечных сечений
стержня.

Нормальные
напряжения в сечении стержня определяем
по формуле (2.1).

Используя эту
формулу, установим закономерности
изменения напряжений на каждом из
участков

, (где i

номер участка).

I
участок
:

II
участок

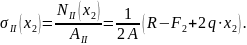
Отсюда следует:

при

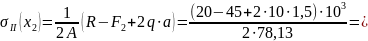
III
участок

Отсюда получим:

при

По полученным
данным строим эпюру

(см. рис. 6, в), порядок построения которой
аналогичен построению эпюры нормальных
сил N(x).

Анализ построенной
эпюры нормальных напряжений показывает,
что лишь в одном, наиболее нагруженном
сечении стержня напряжения достигают
допускаемой величины, а в других
поперечных сечениях напряжения меньше
допускаемых. Это свидетельствует о
правильности подбора площадей поперечных
сечений стержня.

5. Проверка выполнения условия жесткости

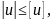
где

– осевое перемещение крайнего правого
сечения стержня.

Согласно (2.10)

Используя формулы
(2.8) или (2.9), определим абсолютные
удлинения (укорочения) участков стержня.

I
участок:

Поскольку

,
то используя формулу (2.9) получим

II
участок:

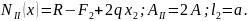
Согласно (2.8) находим

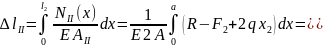
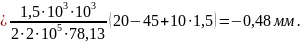
III
участок:

тогда

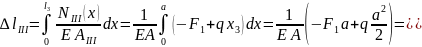
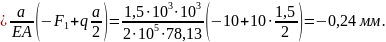
Перемещение
крайнего правого сечения стержня:

Проверяем выполнение
условия жесткости:

Требуемая
жесткость стержня обеспечена. Поэтому
в качестве окончательного принимаем
значение площади A,
установленное из условия прочности.

Примечание.
Если же условие жесткости не выполняется
и

превышает

более чем на 5 %, то значение площади A
определяют из условия жесткости. Для
этого записывают

в аналитическом виде и приравнивая к

,
находят необходимое значение площади
A.
Это значение будет больше того, что было
получено из условия прочности, и его
принимают в качестве окончательного.

2.6.2. Пример решения задачи №2.

Расчёт статически
неопределимой стержневой системы

Абсолютно жесткий
брус (рис. 7), нагруженный сосредоточенной
силой

,
опирается на шарнирно-неподвижную опору
и поддерживается стальными
шарнирно-закрепленными стержнями
круглого поперечного сечения.

Требуется:

Площади поперечных
сечений стержней

взять из расчета по допускаемым
напряжениям.

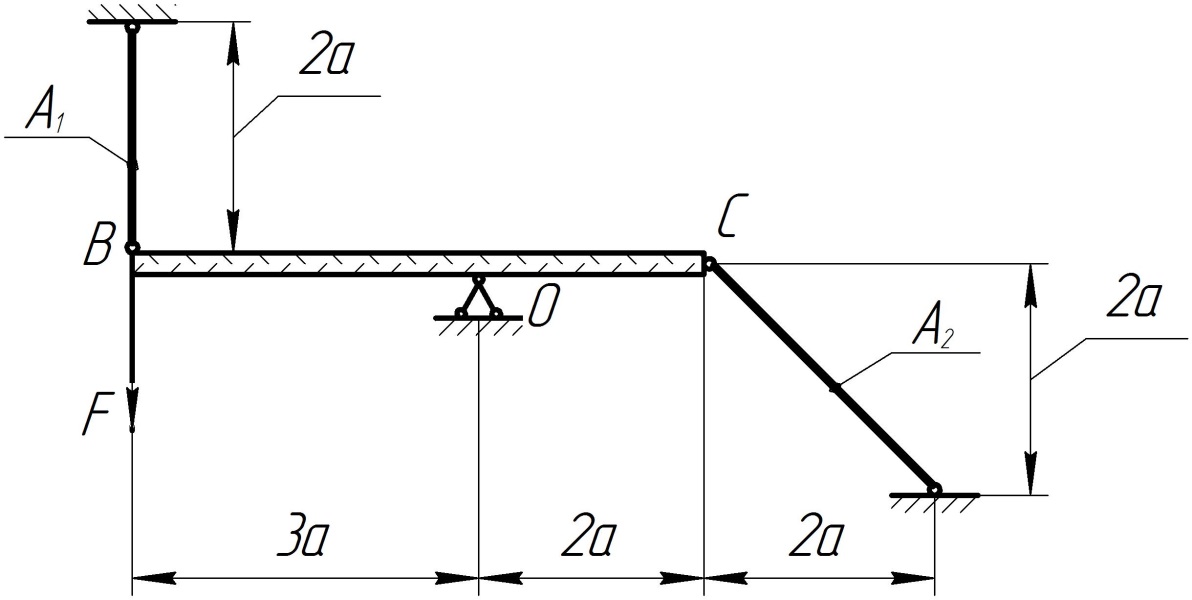
Рис. 7.
Статически неопределимая стержневая
система

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пример решения задачи по расчету размеров поперечного сечения прямого стального стержня по условию прочности на растяжение-сжатие.

Задача

Для прямого стержня постоянного сечения подобрать размер стороны a квадратного сечения по условию прочности. Материал стержня – сталь. Допустимые напряжения [σ]=160 МПа.

Полученные размеры принять согласно ГОСТ 6636.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Предыдущие пункты решения задачи

Определение опорных реакций.
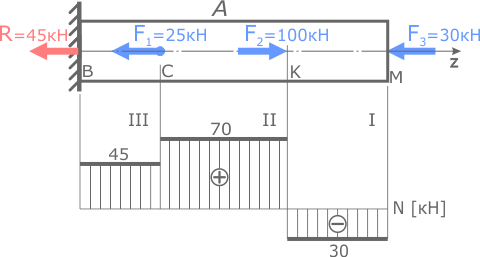
Построение эпюр внутренних продольных сил.

Рассматриваемый стержень нагружен исключительно продольными силами, поэтому для подбора размеров его поперечного сечения воспользуемся условием прочности при растяжении-сжатии.

где N – внутренние продольные силы (найдены ранее),
A — площадь поперечного сечения стержня.

Чтобы найти размеры поперечного сечения стержня рассчитаем площадь A. Для этого запишем условие прочности относительно площади:

Площадь сечения в данном случае постоянна по всей длине стержня и должна обеспечивать прочность на всех его силовых участках. Поэтому расчет будем вести по самому нагруженному из них, т.е. где внутренняя сила максимальна (N_max).

По построенной эпюре внутренних сил видно, что наиболее нагруженным является II участок, где N=N_max=70кН.

Тогда расчетная площадь сечения стержня:

Таким образом для обеспечения необходимой прочности стержня площадь его поперечного сечения должна быть не менее 437,5 мм².

Теперь, зная площадь квадрата, рассчитаем его сторону

Это соответственно минимальный размер поперечного сечения стержня, обеспечивающий его прочность.

В случаях, когда в задании не ставится дополнительных условий полученный размер можно округлить до целого миллиметра, но только в большую сторону.

По ГОСТ 6636 окончательно принимаем ближайший в сторону увеличения линейный размер а=22мм.

Все дальнейшие расчеты стержня будем вести по этому размеру.

Расчет и построение эпюры нормальных напряжений >
Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Чтобы узнать, как правильно рассчитать площадь поперечного сечения стержня колонны, необходимо знать специальные формулы, используемые при проектировании металлических объектов.

Чтобы узнать, как правильно рассчитать площадь поперечного сечения стержня колонны, необходимо знать специальные формулы, используемые при проектировании металлических объектов.

Для понимания вопроса, как правильно рассчитать площадь поперечного сечения стержня колонны, нужно иметь представление о нормативной устойчивости металлического объекта, для которого определяется площадь поперечного сечения стержня колонны.

Только зная эти значения, можно точно распределить площадь поперечного сечения стержня колонны между стенкой и полками и нужно основываться на передаче значительной части на долю полок.

В этом случае будет ясно, как правильно рассчитать площадь поперечного сечения стержня колонны, чтобы повысить заданную устойчивость металлического объекта, но при этом стенка металлического объекта не должна быть тоньше стандартных значений, чтобы не терять параметров ее местной устойчивости.

Как правило, толщину стенки металлического объекта назначают не менее восьми миллиметров, а отношение высоты стенки металлического объекта к толщине металлического объекта
при решении вопроса как правильно рассчитать площадь поперечного сечения стержня колонны принимают в пределах 60-120. Если увеличение местной устойчивости стенки металлического объекта увеличением ее толщины не рационально, то можно укрепить ее продольными ребрами.

Приведенные здесь примеры того, как правильно рассчитать площадь поперечного сечения стержня колонны приблизительны, поэтому не исключают возможных последующих корректировок с учетом требований норм.

Источник

Площадь поперечного сечения стержня с учетом энергии деформации, хранящейся в стержне Калькулятор

Search
Дом	физика ↺
физика	Дизайн машины ↺
Дизайн машины	Проектирование элементов машин ↺
Проектирование элементов машин	Теорема Кастильяно для прогиба в сложных конструкциях ↺

✖Осевая сила на балке определяется как сила сжатия или растяжения, действующая на балку, стержень или вал.ⓘ Осевая сила на балке [P]			+10% -10%
✖Длина стержня или вала определяется как общая длина стержня или вала в соответствии с теоремой Кастиглано.ⓘ Длина стержня или вала [L]			+10% -10%
✖Энергия деформации в стержне или валу определяется как энергия, накопленная в стержне или валу из-за деформации.ⓘ Энергия деформации в стержне или валу [U]			+10% -10%
✖Модуль упругости стержня или вала — это величина, которая измеряет сопротивление объекта или вещества упругой деформации при воздействии на него напряжения.ⓘ Модуль упругости стержня или вала [E]			+10% -10%

✖Площадь поперечного сечения стержня — это площадь двумерной формы, которая получается при разрезании трехмерного стержня перпендикулярно некоторой заданной оси в точке.ⓘ Площадь поперечного сечения стержня с учетом энергии деформации, хранящейся в стержне [A]

⎘ копия

Площадь поперечного сечения стержня с учетом энергии деформации, хранящейся в стержне Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Осевая сила на балке: 55000 Ньютон —> 55000 Ньютон Конверсия не требуется
Длина стержня или вала: 1330 Миллиметр —> 1.33 метр (Проверьте преобразование здесь)
Энергия деформации в стержне или валу: 40 Джоуль —> 40 Джоуль Конверсия не требуется
Модуль упругости стержня или вала: 98000 Ньютон на квадратный миллиметр —> 98000000000 Паскаль (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.000513169642857143 Квадратный метр —>513.169642857143 Площадь Миллиметр (Проверьте преобразование здесь)

14 Теорема Кастильяно для прогиба в сложных конструкциях Калькуляторы

Площадь поперечного сечения стержня с учетом энергии деформации, хранящейся в стержне формула

Площадь поперечного сечения стержня = Осевая сила на балке^2*Длина стержня или вала/(2*Энергия деформации в стержне или валу*Модуль упругости стержня или вала)

A = P^2*L/(2*U*E)

Определить энергию деформации?

Энергия деформации — это тип потенциальной энергии, которая запасается в элементе конструкции в результате упругой деформации. Внешняя работа, совершаемая над таким элементом при его деформировании из ненапряженного состояния, преобразуется и считается равной запасенной в нем энергии деформации.

Источник

ПОДБОР ПОПЕРЕЧНОГО
СЕЧЕНИЯ СТЕРЖНЯ

Последовательность
решения задачи

1. Определить реакции стержней, используя уравнения равновесия для плоской системы сходящихся
сил и проверить правильность найденных реакций.

2. Для
наиболее нагруженного стержня, используя уравнение прочности

определить площадь
поперечного сечения стержня, подобрать по сортаменту (ГОСТ 8509 — 93)
подходящий номер профиля и найти стандартное значение площади поперечного
сечения стержня.

3. Определить
процент недогрузки наиболее нагруженного стержня, используя условие прочности σ
£ [σ], при принятых стандартных размерах
площади поперечного сечения

Пример. Для данной
системы двух стержней одинакового поперечного сечения, нагруженных силой F = 170 кН ( рис.1), определить: а) площадь
поперечного сечения стержней, состоящих из двух равнобоких уголков, и подобрать
по ГОСТу соответствующий профиль уголка; б) определить процент недогрузки
наиболее нагруженного стержня, при принятых стандартных размерах сечения,
приняв [σ] = 140 МПа

Рис. 1 — Схема задачи

Решение:

1. Освобождаем
тело от связей и изображаем действующие на него силы и реакции отброшенных
связей (рис. 2). Выбираем систему координат

Рис. 2 — Реакции связей и выбор систем координат

2. Составляем уравнения равновесия для системы сил, действующих на тело:

å F_i_х= 0; N₂× cos
45° — N₁× cos
60° =
0 (1)

å F_i_у= 0; N₁× cos
30° + N₂× cos
45° — F = 0 (2)

3. Определяем реакции связей N₁ и N₂ решая уравнения.

Из уравнения ( 1 ) получаем

N₁ = N₂ × cos 45° / cos 60° = N₂ × 0,707 / 0,5 = 1,41 N₂ кН

Подставляя найденное значение N₁ в
уравнение ( 2 ), получаем

N₂ = F / 1,41
cos 30° + cos 45° =170 / 1,41× 0,866 — 0,707 = 88,3
кН

N₁ = 1,41 N₂ = 1,41× 88,3 = 124,5 кН

4. Проверим
правильность полученных результатов используя геометрический метод.

5. Строим
замкнутый силовой треугольник, соблюдая параллельность переноса сил и реакций и
расставляем углы (рис. 3).

Рис. 3 — Силовой
треугольник

6. Определяем реакции связей, исходя из теоремы синусов:

N₁ = F × sin 45°/ sin 105°
= 170 × 0,707 / 0,966 = 124,4 кН

N₂ = F × sin 30°/ sin 105°
= 170 × 0,5 / 0,966 = 88 кН

7. Определяем требуемую площадь
поперечного сечения для наиболее нагруженного стержня

N_max = N₁ = 124,5 кН

A₁ = N₁ / [σ] = 124,5 × 10³ / 140 × 10⁶ = 889 × 10^-6 м² = 8,89
см²

т.к. стержень состоит из двух уголков, то площадь уголка вычисляем
по формуле

A_уголка = А₁ / 2 = 8,89 / 2 = 4,445 см²

Подбираем
по сортаменту (ГОСТ 8509 — 93) подходящий номер профиля равнобокого уголка —
это профиль № 5 (50х50х5)
с площадью поперечного сечения [А] = 4,8 см²

Таким
образом, требуемая
площадь поперечного сечения для наиболее нагруженного стержня

А = 2 × [А] = 2 × 4,8 = 9,6 см²

8. Определяем рабочее напряжение в
поперечном сечении для наиболее нагруженного стержня и проверяем прочность
стержня

σ = N₁ / А = 124,5 × 10³ / 9,6 10^-4=
12,97× 10⁷Па = 129,7 МПа

σ
£ [σ]

129,7 МПа £ 140 МПа — условие прочности
соблюдено.

9. Определяем процент недогрузки наиболее нагруженного стержня

Недогруз
составляет 7,35 %

ГОСТ 8509-93

Уголки стальные горячекатаные равнополочные.

Сортамент (извлечение)

Обозначения:

b – ширина
полки;

t –
толщина полки;

R – радиус
внутреннего закругления;

F – площадь
поперечного сечения;

I – момент
инерции;

i – радиус
инерции;

x₀ – расстояние от центра тяжести до наружной грани полки

Задача 1. Задана система двух стержней, составленных из двух равнобоких уголков. При
заданном значении
силы F, определить: а)
площадь поперечного сечения стержней и подобрать по ГОСТ 8509 — 93
соответствующий профиль уголка; б) определить процент недогрузки наиболее
нагруженного стержня, при принятых стандартных размерах сечения, приняв [σ] = 160 МПа. Массой стержней пренебречь. Схему своего варианта смотри на
рисунке 4. Числовые данные своего варианта взять из таблицы 1.