Как найти площадь параллелограмма авсд 8 класс - Avtoru.top

Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.

Формула вычисления площади
- По длине стороны и высоте
- По двум сторонам и углу между ними
- По двум диагоналям и углу между ними
Примеры задач

Формула вычисления площади

По длине стороны и высоте

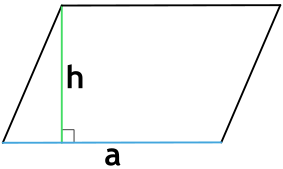
Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

По двум сторонам и углу между ними

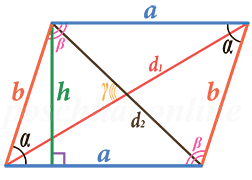
Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:

S = a ⋅ b ⋅ sin α

По двум диагоналям и углу между ними

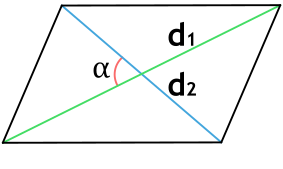
Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:

S = ¹/₂ ⋅ d₁ ⋅ d₂ ⋅ sin α

Примеры задач

Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.

Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см².

Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.

Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см².

Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.

Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см².

Источник

{S = a cdot h}

Найти площадь параллелограмма

На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные — основание, высоту, стороны, диагонали и углы между ними и получите ответ.

Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).

Содержание:

калькулятор площади параллелограмма
формула площади параллелограмма через сторону и высоту
формула площади параллелограмма через две стороны и угол между ними
формула площади параллелограмма через диагонали и угол между ними
примеры задач

Формула площади параллелограмма через сторону и высоту

{S = a cdot h}

a — сторона параллелограмма

h — высота параллелограмма

Формула площади параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}

a, b — стороны параллелограмма

α — угол между сторонами a и b

Формула площади параллелограмма через диагонали и угол между ними

{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}

d₁, d₂ — диагонали параллелограмма

α — угол между диагоналями

Примеры задач на нахождение площади параллелограмма

Задача 1

Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.

Решение

Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.

S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2

Ответ: 108 cdot 0.866 approx 93.53074 : см^2

Мы можем проверить ответ с помощью калькулятора .

Задача 2

Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.

Решение

Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.

S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2

Ответ: 48 см²

И снова проверить ответ нам поможет калькулятор .

Задача 3

Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.

Решение

В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.

S = a cdot h = 12 cdot 8 = 96 : см^2

Ответ: 96 см²

И снова проверить ответ нам поможет калькулятор .

Источник

Как найти площадь параллелограмма

Главная
/
Математика
/
Геометрия
/
Как найти площадь параллелограмма

Чтобы найти площадь параллелограмма воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.

Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):

длину стороны a и длину высоты h
длины сторон a и b, и угол α
длины сторон a и b, и угол β
длины сторон a и b, и длину любой из диагоналей (d₁ или d₂)
длины диагоналей d₁ и d₂, и угол между ними γ

Подставьте значения в соответствующие поля и получите результат.

Зная длину стороны a и длину высоты h

Чему равна площадь параллелограмма если сторона

a = ,

а высота

h = ?

Ответ: S =

Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?

Формула

S = a⋅h

Пример

Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:

S = 8 ⋅ 4 = 32 см²

Зная длины сторон a и b, и угол α

Чему равна площадь параллелограмма если сторона

a = ,

сторона

b = ,

а угол между ними

α = °

?
Ответ: S =

Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?

Формула

S = a⋅b⋅sinα

Пример

Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:

S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см²

Зная длины сторон a и b, и угол β

Чему равна площадь параллелограмма если сторона

a = ,

сторона

b = ,

а угол между ними

β = °

?
Ответ: S =

Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?

Формула

S = a⋅b⋅sin(180 — β)

Пример

Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:

S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см²

Зная длины сторон a и b, и длину диагонали (d₁ или d₂)

Чему равна площадь параллелограмма если сторона

a = ,

сторона

b = ,

а диагональ

d =

?
Ответ: S =

Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?

Формула

S = 2√p⋅(p-a)⋅(p-b)⋅(p-d), где p=(a+b+d)/2

Пример

Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:

p = (8 + 5 +11)/2 = 12

S = 2√12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅√12⋅4⋅7⋅1 = 2⋅√336 = 36.66 см²

Зная длины диагоналей d₁ и d₂, и угол между ними γ

Чему равна площадь параллелограмма если диагональ

d₁ = ,

диагональ

d₂ = ,

а угол между ними

γ = °

?
Ответ: S =

Чему равна площадь параллелограмма S если известны длины диагоналей d₁ и d₂, и угол между ними γ?

Формула

S = ½⋅d₁⋅d₂⋅sinγ

Пример

Если диагональ параллелограмма d₁ = 11 см, диагональ d₂ = 7 см, а ∠γ = 45° то:

S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см²

См. также

Источник

Определение параллелограмма

Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.

Онлайн-калькулятор площади параллелограмма

Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.

Рассмотрим несколько способов и формул с последующим решением простых примеров.

Формула площади параллелограмма по основанию и высоте

Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.

Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:

S=a⋅hS=acdot h

aa — основание;
hh — высота.

Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.

Пример

Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).

Решение

a=10a=10
h=5h=5

Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)

Ответ: 50 (см. кв)

Формула площади параллелограмма по двум сторонам и углу между ними

В этом случае искомая величина находится так:

S=a⋅b⋅sin⁡(α)S=acdot bcdotsin(alpha)

a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.

Теперь решим другой пример и воспользуемся вышеописанной формулой.

Пример

Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.

Решение

a=20a=20
p=100p=100
α=30∘alpha=30^{circ}

Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30

Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin⁡(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)

Ответ: 300 (см. кв.)

Формула площади параллелограмма по диагоналям и углу между ними

S=12⋅D⋅d⋅sin⁡(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)

DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.

Пример

Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.

Решение

D=10D=10
d=5d=5
α=30∘alpha=30^{circ}

S=12⋅10⋅5⋅sin⁡(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)

Ответ: 12.5 (см. кв.)

Решение контрольной работы по геометрии онлайн — от профильных экспертов Студворк!

Тест по теме «Площадь параллелограмма»

Источник

Тип урока: изучение нового материала.

Цели:

Повторить площадь прямоугольника.
Вывести формулу площади параллелограмма.
Применять формулу площади параллелограмма при решении задач.

Планируемые результаты:

Предметные:

Познакомиться с формулой площади параллелограмма и ее доказательством.
Научиться выводить формулу площади параллелограмма и находить площадь параллелограмма, используя формулу, решать задачи.

Метапредметные:

Коммуникативные: с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.
Регулятивные: выделять и осознавать то, что уже усвоено и что еще подлежит усвоению, осознавать качество и уровень усвоения.
Познавательные: сопоставлять характеристики объектов по одному или нескольким признакам; выявлять сходства и различия объектов.

Виды деятельности: формирование у учащихся умений построения и реализации новых знаний, выполнение практических заданий.

Оборудование: доска, мел, линейка, учебник, наглядность, проектор, мультимедийная презентация.

Учебник (УМК): Геометрия 7-9, Л.С.Атанасян, В.Ф.Бутузов, 2015.

1. Приветствие

2. Проверка домашнего задания

Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.

Дано:

АВСД — прямоугольник
Р= 60
АВ:ВС=4:11

Найти: S.

Решение:

Пусть 1 часть равна х, тогда АВ=4х, ВС=11х, составим и решим уравнение:

Р=2(АВ+ВС),
60=2(4х+11х),
60=30х,
х=2.
АВ=4·2=8
ВС=11 ·2=22
S=АВ · ВС=8 ·22=176.

Ответ:176

3. Мотивация на учебную деятельность

Устная работа.

Найти площади фигур:

Какой вывод можно сделать?

(- Все фигуры имеют одинаковую площадь.

— Фигуры № 1,2,3 равны, а у равных фигур равные площади.

— Фигуры №1,4 или 2,4 или 3,4 имеют равные площади, но сами они разные.)

Такие фигуры называются равновеликими. Фигуры № 3,4 называют равновеликими, так как их площади равны, но сами фигуры не равны.

4. Целеполагание. Постановка проблемы. Поиск путей решения проблемы

Решим задачу.

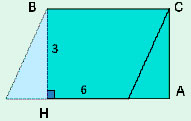
Дано:

АВСД — параллелограмм

АД – основание, АД=6

ВН — высота, ВН=3

Найти: S.

Надо 6 · 3?

То есть использовать формулу площади прямоугольника?

А как читается данная формула? (Площадь прямоугольника равна произведению его смежных сторон.)

А ВН и АД разве смежные?

Что можно сделать, чтобы мы получили прямоугольник? (Надо ∆АВН переместить вправо и получим прямоугольник.)

Тогда прямоугольник и параллелограмм будут какими фигурами? (Равновеликими).

Решение:

S=АД · ВН = 6 · 3 = 18.

Мы можем заменить параллелограмм на равновеликую фигуру прямоугольник => можно утверждать, что их площади равны.

Ответ: 18.

5. Тема урока: Площадь параллелограмма

Цели урока:

Вывести формулу площади параллелограмма.
Решить задачи на вычисление площади параллелограмма.

Решение проблемы

Выведем формулу площади параллелограмма.

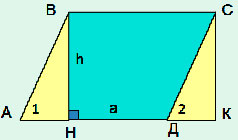
Теорема: площадь параллелограмма равна произведению его основания на высоту.

Дано:

АВСД — параллелограмм
S — площадь,
а — основание,
h – высота.

Доказать: S = аh.

Доказательство:

Дан параллелограмм АВСД:

1) достроим параллелограмм АВСД до трапеции АВСК;

2) рассмотрим ∆АВН и ∆ДСК:

а) АВ=СД (противоположные стороны параллелограмма),

б) 1= 2 (соответственные углы при АВ || СД и АД – секущей), значит ∆АВН = ∆ДСК (по гипотенузе и острому углу) => SАВН=SДСК.

3) SВНКС = аh (по теореме о площади прямоугольника);

4) SАВСД + SСДК = SАВН + SВНКС,

SАВСД = SВНКС (так как ∆АВН = ∆ДСК),

SАВСД = аh.

6. Первичное закрепление

Работа устно.

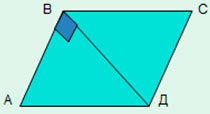
Дано:

АВСД — параллелограмм
АВ=10
ВД — высота, ВД=12

Найти: S.

Чему равняется площадь параллелограмма? (Произведение основания на высоту.)

А АВ основание? (Нет, но к ней проведена высота, значит можно утверждать, что АВ является основанием.)

Верно, то есть высота всегда проведена к основанию.

Решение:

S=ВД · ВА = 12 · 10 = 120.

Ответ: 120.

7. Письменная работа

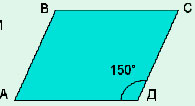
Дано:

АВСД — параллелограмм
АВ=14
ВС=18

Д = 150°

Найти: S.

Решение:

Что надо сделать?

1) Построить высоту ВН.

2) Рассмотрим ∆АВН:

А=180°-Д=180°-150°= 30° (соответственные углы при СВ || АД и АВ – секущей)

ВН =½АВ=½· 14=7 (катет, лежащий напротив угла в 30° равен половине гипотенузы)

3) SАВСД =АД · ВН = 18 · 7 = 126. (АД=ВС как противоположные стороны параллелограмма).

Ответ: 126.

8. Домашнее задание

Открываем дневники и записываем домашнее задание: Выучить формулировку и доказательство теоремы, № 459.

!!! Обратите внимание!!! Вы будете находить не только площадь параллелограмма, но и основание и высоту. Вы будете работать с данной формулой.

9. Рефлексия

Что сегодня я узнал (а)?
Я научился(ась) чему-то новому?
Я понял (а) материал или были затруднения?

10. Резерв

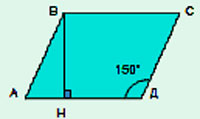
Дано:

АВСД — параллелограмм
АВ=ВС=10
В = 150°

Найти: S.

Решение:

1) Построить высоту ВН.

2) Рассмотрим ∆АВН:

А=180° – Д=180°-150°= 30° (соответственные углы при ВС || АД и АВ – секущей)

ВН=½АВ= ½· 10=5 (катет лежащий напротив угла в 30° равен половине гипотенузы)

3) SАВСД =АД · ВН = 10 · 5 = 50. (АД=ВС как противоположные стороны параллелограмма).

Ответ: 50.

Источник

Формула вычисления площади

По длине стороны и высоте

По двум сторонам и углу между ними

По двум диагоналям и углу между ними

Примеры задач

Содержание:

Формула площади параллелограмма через сторону и высоту

Формула площади параллелограмма через две стороны и угол между ними

Формула площади параллелограмма через диагонали и угол между ними

Примеры задач на нахождение площади параллелограмма

Как найти площадь параллелограмма

Онлайн калькулятор

Зная длину стороны a и длину высоты h

Формула

Пример

Зная длины сторон a и b, и угол α

Формула

Пример

Зная длины сторон a и b, и угол β

Формула

Пример

Зная длины сторон a и b, и длину диагонали (d1 или d2)

Формула

Пример

Зная длины диагоналей d1 и d2, и угол между ними γ

Формула

Пример

См. также

Онлайн-калькулятор площади параллелограмма

Формула площади параллелограмма по основанию и высоте

Формула площади параллелограмма по двум сторонам и углу между ними

Формула площади параллелограмма по диагоналям и углу между ними

Тест по теме «Площадь параллелограмма»

1. Приветствие

2. Проверка домашнего задания

3. Мотивация на учебную деятельность

4. Целеполагание. Постановка проблемы. Поиск путей решения проблемы

5. Тема урока: Площадь параллелограмма

Решение проблемы

6. Первичное закрепление

7. Письменная работа

8. Домашнее задание

9. Рефлексия

10. Резерв

Не пропустите также:

Зная длины сторон a и b, и длину диагонали (d₁ или d₂)

Зная длины диагоналей d₁ и d₂, и угол между ними γ