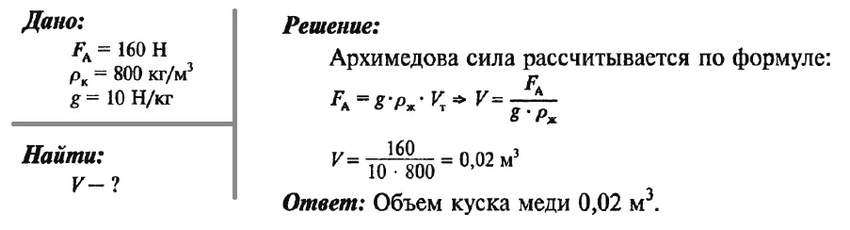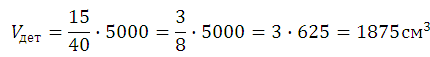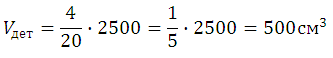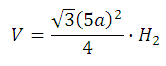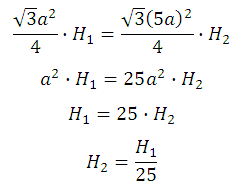Как найти площадь основания сосуда с водой

Площадь сечения сосуда

Сосуд — это емкость, предназначенная для ведения химических, тепловых и других технологических процессов, а также для хранения. Основными математическими характеристиками сосуда являются диаметр основания и высота.

Сечение сосуда — это изображение фигуры, образованной рассечением сосуда плоскостью в поперечном или продольном направлении.

Формула для расчета площади поперечного сечения сосуда:

S = π * d 2 / 4, где

d — диаметр сосуда.

Формула для расчета площади осевого сечения сосуда:

d — диаметр сосуда;
h — высота сосуда.

Формула для расчета площади параллельного оси сечения сосуда (бокового сечения сосуда):

a — хорда основания сосуда;
h — высота сосуда.

Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного или продольного сечения сосуда, если известны диаметр сосуда, длина хорды и высота сосуда. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения сосуда (площадь осевого сечения сосуда, площадь параллельного сечения сосуда, площадь бокового сечения сосуда и площади поперечного сосуда).

Источник

Статика. Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление).

Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то дав­ление, которое существует внутри них благодаря весу собственных частей.

Давление, оказываемое покоящейся жидкостью, называется гидроста­тическим.

Получим формулу для расчета гидростатического давления жидкости на произвольной глубине h (в окрестности точки A на рисунке).

Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:

1) как произведение давления p в основании этого столба на площадь его сечения S:

2) как вес того же столба жидкости, т. е. произведение массы m жидкости на ускорение сво­бодного падения:

Масса жидкости может быть выражена через ее плотность p и объем V:

а объем — через высоту столба и площадь его поперечного сечения:

Подставляя в формулу (1.28) значение массы из (1.29) и объема из (1.30), получим:

Приравнивая выражения (1.27) и (1.31) для силы давления, получим:

Разделив обе части последнего равенства на площадь S, найдем давление жидкости на глубине h:

Это и есть формула гидростатического давления.

Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободно­го падения и глубины, на которой определяется давление.

Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе, давление на стенки сосуда, а так­же давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.

Гидростатический парадокс .

Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.

В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.

Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужа­ющихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.

Это следует из того, что давление покоящейся жидкости зависит только от глубины под свободной поверхностью и от плотности жидкости: p = pgh (формула гидростатического давления жидкости). А так как площадь дна у всех сосудов одинакова, то и сила, с которой жидкость давит на дно этих сосу­дов, одна и та же. Она равна весу вертикального столба ABCD жидкости: P = oghS, здесь S — площадь дна (хотя масса, а следовательно, и вес в этих сосудах различны).

Гидростатический парадокс объясняется законом Паскаля — способ­ностью жидкости передавать давление одинаково во всех направлениях.

Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное дав­ление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давле­ние. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, подняв­шись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давле­ние в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Источник

Как найти площадь основания сосуда с водой

Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».

Название величины

Обозначение

Единица измерения

Формула

Объем тела

V_т = F_A / pg

Плотность жидкости

кг/м 3

p_ж = F_A / (Vg)

Сила Архимеда

F_A = p_ж V_т g

Постоянная

g ≈ 10 Н/кг

Физика 7 класс: все формулы и определения МЕЛКО на одной странице

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Тело объемом 2 м 3 погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2. Определить выталкивающую силу, действующую на деревянный плот объемом 12 м 3 , погруженный в воду на половину своего объема.

Задача № 3. Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4. Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5. Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6. Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

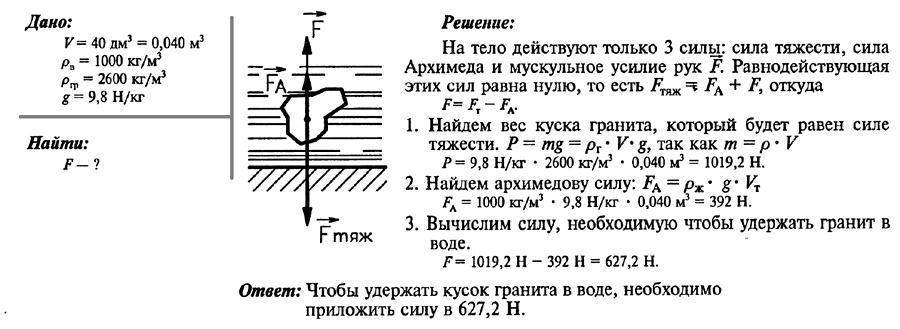
Задача № 7. Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм 3 ?

Задача № 8. Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.

Задача № 9 (повышенной сложности). Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности). Рассчитайте, какой груз сможет поднять шар объемом 1 м 3 , наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11. Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м 3 .

Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V₁ – объем цилиндра, погруженного в масло (V₁ = V – V₂ = Sh₁); h₁ – высота части цилиндра, погруженной в масло; V₂ – объем цилиндра, погруженного в воду после добавления масла; р_в – плотность воды (1000 кг/м 3 ); р_м – плотность масла (800 кг/м 3 )

Найти : (h – h₁) / h — ?

Решение . F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9p_вgV
F₁ – сила, выталкивающая цилиндр из масла F₁ = p_мgV₁
F₂ – сила, выталкивающая цилиндр из воды после добавления масла F₂ = p_вgV₂
Баланс сил: F – F₁ = F₂
0,9p_вgV – p_мgV₁ = p_вgV₂ V₁ = V – V₂ ⇒ 0,9p_вV – p_м(V – V₂) = p_вV₂

V(0,9p_в – p_м) = V₂(p_в – p_м) V = Sh; V₁ = Sh₁ ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).

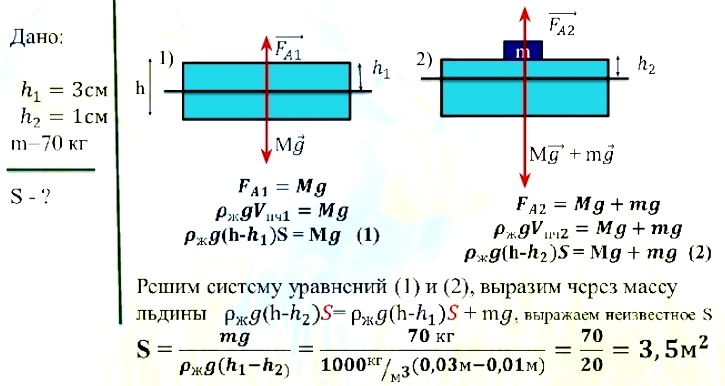
Задача № 12. Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.

Ответ: 3,5 м 3 .

Теория для решения задач.

Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = р_атм + p*g*h

Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».

Источник

Как уровень воды зависит от площади дна сосуда?

Блин! Тут вопрос не о давлении! А об объёме!

Если один и тот же объём наливать в сосуды с разным по площади дном, то высота столба воды/её уровень будет зависеть от размеров дна.

Если предположить, что сосуд имеет форму параллепипеда, то уровень объёма жидкости V будет связан с дном формулой:

V = Sд * h, где Sд — площать дна, а h — уровень. Отсюда h = V/Sд, где площадь дна рассчитыаем по формуле: Sд = a * b, где а — длина сосуда, b — ширина сосуда. h в данном случае — минимальная высота сосуда, что бы влезла вся жидкость объёма V.

Для цилиндра, формула та же: V = Sд * h. Только площадь дна считается по формуле:

Sд = Пи * D в квадрате. Пи — число Пи.

Это всё случаи если сосуд или цилиндр или параллелепипед. В случае сосуда в виде шара так не посчитать, так как в данном случае в точке соприкосновения шара и поверхности площадь дан равна нулю. Тогда чтобы вычислить высоту, которую в шаре занял объём жидкости, нужно уже будет прибегать к вычислению объёма через интеграл. Тем не менее, минимальный объём шара и, следовательно, его диаметр посчитать легко — формула объёма шара известна.

V = 4/3 Пи * R в кубе, где Пи — число Пи, R — радиус шара. Если выразить R через D — диаметр шара, получим:

V = 4/3 Пи * (D/2)в кубе = 4/3 Пи * D в кубе / 8 = Пи * D в кубе / 6

Диаметр шара, полученный из этой формулы, будет минимальным, чтобы вместился весь объём:

D = Корень кубический из (6 * V / Пи).

Этот диаметр и будет высотой h для данного объёма.

Для других случаев нужно будет уже выводить всё через интеграл от объёма.

Источник

Расчёт давления жидкости на дно и стенки сосуда

Тип урока: Урок открытия и первичного закрепления знаний.

Цель урока: получить выражение для расчёта давления жидкости на дно и стенки сосуда; проверка качества знаний учащихся при решении задач.

Задачи урока:

• Предметные: углубить и закрепить знания о давлении жидкости.
• Метапредметные: продолжить развивать внимание, память, логическое мышление, умение делать выводы.
• Личностные: способствовать формированию научного мировоззрения, активизировать учебно-познавательную деятельность учащихся, содействовать формированию самостоятельности, воспитанию интереса к предмету.

Оборудование к уроку: компьютер, видеопроектор, интерактивная доска, два стакана с водой, цилиндрические сосуды с основаниями различной площади, деревянный брусок, камень, два одинаковые пластмассовые груза, широкий сосуд, аквариум, удочка, каточки с заданиями, учебник по физике.

Ход урока

1.Организационный момент.

2. Актуализация имеющихся знаний.

Взаимопроверка в парах по вопросам. Слайд 1

1. Чем отличается процесс передачи давления в жидкости и газе от передачи давления твёрдыми телами? (давление твёрдыми телами передаётся в направлении действия силы, в жидкости и газе по всем направлениям одинаково)
2. Сформулируйте закон Паскаля. (давление, производимое на жидкость или газ, передаётся в любую точку без изменений во всех направлениях)
3. Мальчик выдувает мыльные пузыри. Почему они принимают форму шара? (они приобретают форму шара, так как давление в газе, согласно закону Паскаля передаётся одинаково по всем направлениям)
4. От чего зависит давление газа? (от объёма, массы и температуры газа)
5. Для космонавтов пищу изготавливают в полужидком виде и помещают в тюбики с эластичными стенками. Что помогает космонавтам выдавливать пищу из тюбиков? (Закон Паскаля)
6. Почему взрыв снаряда под водой губителен для живущих в воде организмов? (давление взрыва в жидкости, согласно закону Паскаля, передаётся одинаково по всем направлениям, и от этого животные могут погибнуть)
7. Почему пловец, нырнувший на большую глубину, испытывает боль в ушах? (с глубиной давление увеличивается; пловец испытывает боль в ушах, так как вода с большой силой давит на барабанные перепонки)

3. Открытие нового знания. Слайд 2

В три сосуда с одинаковой площадью дна, стоящие на столе, налили воды до одного уровня

1) В каком сосуде масса воды больше? Меньше?

2) Одинаковым ли будет давление воды на дно сосудов?

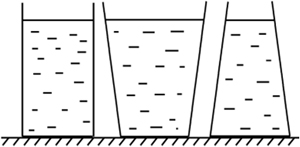
Вы уверены? Как рассчитать давление жидкости на дно сосуда? (Затруднение).

• Какая цель нашего урока? (Узнать, как рассчитать давление жидкости на дно сосуда)
• Какая тема урока? (Расчёт давления жидкости на дно и стенки сосуда) Слайд 3

Учащиеся записывают тему к себе в тетрадь.

Попытаемся вывести формулу для расчёта этого давления. Но какую же форму сосуда нам надо выбрать для расчёта нашей формулы? Я предлагаю взять форму прямоугольного параллелепипеда.

Для того чтобы упростить вывод формулы для расчета давления на дно и стенки сосуда, удобнее всего использовать сосуд в форме прямоугольного параллелепипеда (Рис. 2).

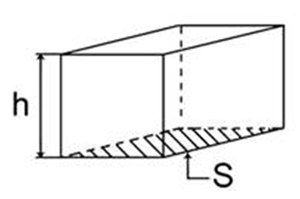
Рис. 2. Сосуд для расчета давления жидкости

Площадь дна этого сосуда – S, его высота – h. Предположим, что сосуд наполнен

жидкостью на всю высоту h. Чтобы определить давление на дно, нужно силу,

действующую на дно, разделить на площадь дна. В нашем случае сила – это вес жидкости P, находящейся в сосуде

Поскольку жидкость в сосуде неподвижна, ее вес равен силе тяжести, которую можно вычислить, если известна масса жидкости m.

Напомним, что символом g обозначено ускорение свободного падения.

Для того чтобы найти массу жидкости, необходимо знать ее плотность ρ и объем V

Объем жидкости в сосуде мы получим, умножив площадь дна на высоту сосуда

Эти величины изначально известны. Если их по очереди подставить в приведенные выше формулы, то для вычисления давления получим следующее выражение:

В этом выражении числитель и знаменатель содержат одну и ту же величину S – площадь дна сосуда. Если на нее сократить, получится искомая формула для расчета давления жидкости на дно сосуда:

p = ρgh

Итак, для нахождения давления необходимо умножить плотность жидкости на величину ускорения свободного падения и высоту столба жидкости.

Полученная выше формула называется формулой гидростатического давления. Согласно этой формуле гидростатическое давление не зависит от формы сосуда, в котором находится жидкость и от площади его сечения. Оно зависит от высоты столба жидкости и от плотности жидкости.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов? (одинаковым)

Данная формула позволяет найти давление на дно сосуда. А как рассчитать давление на боковые стенки сосуда? Чтобы ответить на этот вопрос, вспомним, что на прошлом уроке мы установили, что давление на одном и том же уровне одинаково во всех направлениях. Это значит, давление в любой точке жидкости на заданной глубине h может быть найдено по той же формуле.

Возвратимся к нашему вопросу: Одинаковым ли будет давление воды на дно сосудов?

4. Физминутка (под медленную, спокойную мелодию)

— Я предлагаю вам, ребята, выполнить дыхательную гимнастику:

1-е упр. Набрать воздух в лёгкие (вдыхаем медленно, но как можно больше воздуха),

2-е упр. Руки медленно поднимаем вверх и делаем (одновременно) глубокий вдох.

Руки опускаем – выдох.

3-е упр. Глубоко вдохнуть, садясь за парту, медленно выдыхаем (гимнастика проводится под спокойную музыку).

— Сейчас вы выполнили дыхательную гимнастику, которую врачи рекомендуют проводить 3-4 раза в день.

— А какой физический закон лежит в основе дыхательной гимнастики, как он называется? (в основе дыхательной гимнастики лежит закон Паскаля)

5. Закрепление материала.

а) Проведение игры «рыбалка»

1. Куда бы вы перелили сок из литровой банки, чтобы его давление на дно сосуда стало больше: в пятилитровую кастрюлю или в литровую бутылку? (в литровую бутылку)
2. Какие из жидкостей: вода или керосин оказывает меньшее давление на дно сосудов одной формы, если объёмы жидкостей одинаковы? (керосин)
3. Как изменится давление воды на дно доверху наполненного стакана, если в воду опустить камень? (не изменится)
4. В цилиндрический сосуд, частично наполненный водой, опустили деревянный брусок. Как изменится давление воды на дно сосуда? (увечится)
5. Два одинаковых предмета были опущены в цилиндрические сосуды с основаниями различной площади. В цилиндрических сосудах уровень воды до погружения предмета одинаков. В каком сосуде гидростатическое давление больше? (в сосуде меньшей площади)

Ответы на задачи подтверждаются опытами.

б) Расчётные задачи:

1. упр. 17(2)
2. Определите высоту столба керосина, который оказывает давление на дно сосуда равное 8 кПа. Слайд 4

Самостоятельная работа по решению задачи упр.17(1) по рядам?

6. Подведение итогов урока. Рефлексия.

Подведём итоги.

Давайте вспомним, что сегодня делали на уроке, что узнали?

Мне очень важно, с каким настроением вы уходите с урока. Поэтому я прошу вас заполнить лист самоанализа, который находится столах у каждого из вас.

Источник

Друзья! В заданиях ЕГЭ по математике встречаются задачи, в которых речь идёт о погружении детали в жидкость или о переливании жидкости из одного сосуда в другой. Вопросы в условии связаны с нахождением объёма погружаемого в жидкость тела или с нахождением какого-либо параметра сосуда. Форма сосуда может быть различной: цилиндр, призма.

Что необходимо понимать? Если жидкость залита в цилиндрический сосуд, то она принимает форму цилиндра. Если она залита в имеющий форму призмы, то соответственно принимает форму призмы. Это означает, что формулы для объёмов цилиндра и призмы работают и для объёмов жидкостей помещённых в такие сосуды.

Формула объёма цилиндра (и призмы):

Если жидкость переливается в аналогичный сосуд с меньшим основанием, уровень (высота) жидкости увеличивается; если в сосуд с большим основанием, то уровень жидкости уменьшается.

Рекомендации!

В задачах на погружение детали в жидкость следует найти объём полученный после её погружения, далее найти разность объёмов до и после (если данные в условии это позволяют). Можно такие задачи решать и другим способом, используя закон Архимеда. Примеры рассмотрены ниже.

В задачах, где идёт речь о переливании жидкости в другой сосуд (с уменьшенной или увеличенной площадью основания) помните о том, что сам объём жидкости остаётся неизменным. Вы можете выразить его через площадь основания и высоту (S₁ и H₁) одного сосуда и площадь основания и высоту (S₂ и H₂) другого сосуда, далее полученные выражения приравнять.

При дальнейших преобразованиях получите отношение соответствующих величин – либо площадей оснований, их рёбер, либо высот. Пример такой задачи рассмотрен ниже в статье.

В цилиндрический сосуд налили 5000 см³ воды. Уровень жидкости оказался равным 40 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 15 см. Чему равен объем детали? Ответ выразите в см³.

Мы знаем, что объём цилиндра равна произведению площади основания на высоту:

В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.

Высота это есть уровень жидкости.

Итак, из имеющихся данных можем найти площадь основания:

Основание цилиндра у нас величина неизменная, но изменилась высота жидкости (при погружении детали) на 15 сантиметров, то есть она стала  

40 +15 = 55 см.

Найдём полученный объём:

Теперь можем вычислить объём детали:  6875 – 5000 = 1875 см³

Можно решать подобные задачи более рациональным способом.

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 15/40  исходного объема:

Ответ: 1875

Решить самостоятельно:

Посмотреть решение

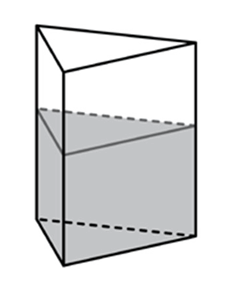
В сосуд, имеющий форму правильной треугольной призмы, налили 2500 см³ воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 20 см до отметки 24 см. Чему равен объем детали? Ответ выразите в см³.

Принцип решения тот же самый, что и в предыдущей задаче.

Мы знаем, что объём призмы равен произведению площади основания на высоту:

В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.

Из имеющихся данных можем найти площадь основания призмы:

Основание призмы  не изменилось, но изменилась высота жидкости (при погружении детали)  она стала 24см.

Найдём полученный объём:

Теперь можем вычислить объём детали:  3000 – 2500 = 500 см³

Второй способ:

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 4/20  исходного объема:

Ответ: 500

Решить самостоятельно:

Посмотреть решение

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 250 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 5 раз больше, чем у первого? Ответ выразите в см.

В подобных задачах с переливаниями жидкости следует помнить, что объём её остаётся прежним (он не изменен – куда бы её не перелили).

Объем жидкости в данном случае это объём правильной  треугольной призмы  (в её основании лежит правильный треугольник). Он равен произведению  площади основания призмы на высоту:

Суть дальнейших действий сводится к тому, что мы можем выразить объёмы жидкостей в двух призмах: первой и второй (основание которой в 4 раза больше), а затем приравнять полученные выражения, в итоге после преобразований получим отношение двух высот.

Естественно, что высота жидкости уменьшится, если увеличить площадь основания.

Обозначим исходную высоту жидкости Н₁, полученную после переливания Н₂.

Найдём площадь основания призмы, обозначив его сторону как а. Площадь правильного треугольника равна:

Таким образом, объём залитой жидкости  в первую призму равен:

Площадь основания второй призмы равна:

Объём залитой жидкости  во вторую призму равен:

Найдём отношение высот:

Таким образом, при том же объёме жидкости её высота уменьшится в 25 раз и будет равна 10.

Или можно сказать так:

При увеличении стороны основания а в 5 раз уровень воды уменьшится в 25 раз.

Ответ: 10

Решить самостоятельно:

Посмотреть решение

В цилиндрический сосуд, в котором находится 14 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему равен объем детали? Ответ выразите в литрах.

Объём цилиндра равна произведению площади его основания на высоту:

Жидкость в сосуде имеет цилиндрическую объёмную форму.

Уровень жидкости поднялся в 1,1 раза – означает, что высота цилиндра увеличилась в 1,1 раза. Исходя из формулы объёма цилиндра понятно, что при увеличении высоты в 1,1 раза влечёт за собой увеличение объёма также в 1,1 раза (так как зависимость величин  прямопропорциона).

Это означает, что после погружения детали объём будет равен 14∙1,1 = 15,4 литра.

Таким образом, объём детали будет равен: 15,4 – 14 = 1.4 литра.

Ответ: 1,4

Решить самостоятельно:

Посмотреть решение

Если ход решения сразу не увидели, ставьте вопрос – что можно найти исходя из условия?

Например, если дан начальный объём и высота жидкости (в сосуде формы призмы или цилиндра), то мы можем найти площадь основания. Затем, зная площадь основания и высоту жидкости после погружения детали мы можем найти объём.

Далее вычислить разницу между объёмами не составит труда  (это относится к первым двум задачам). В последней задаче для решения требуется немного логики.

В задачах по стереометрии на ЕГЭ есть много таких, где требуется найти изменение объёма или площади поверхности (шара, призмы, куба, пирамиды, конуса), при изменении одного из линейных размеров, имеются задачи и обратные им.

В данной рубрике мы рассмотрим такие задачи, не пропустите!

На десерт видео,  отдохнём от математики.

Успехов вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

В задаче требуется найти объём детали, которую погрузили в сосуд с водой.

По закону Архимеда объем детали равен объему вытесненной жидкости.

Вычислим объём вытесненой жидкости по формуле (displaystyle V=S_{осн} cdot triangle hsmall. )

(displaystyle S_{осн}=92 small. )

(displaystyle triangle h=2 small. )

Получаем

(displaystyle V=S_{осн} cdot triangle hsmall, )

(displaystyle V=92 cdot 2=184 small. )

Значит, объём детали равен (displaystyle 184) см³.

Ответ: (displaystyle 184{small .}) 

В цилиндрический сосуд налили

Дата: 2018-04-24

3507

Категория: Стерео Цилиндр Конус

Метка: ЕГЭ-№2

27045. В цилиндрический сосуд налили 2000 см³ воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см³.

Мы знаем, что объём цилиндра равна произведению площади основания на высоту:

В жидкость погружаем деталь. Её уровень поднимается. Для того, чтобы вычислить объём детали необходимо из полученного объёма (полученного после погружения детали) вычесть объём жидкости, который был изначально.

*Высота это есть уровень жидкости. Итак, из имеющихся данных можем найти площадь основания:

Основание цилиндра у нас величина неизменная, но изменилась высота жидкости (при погружении детали) на 9 сантиметров, то есть она стала равна  12 + 9 = 21 см.

Найдём полученный объём (после погружения):

Теперь можем вычислить объём детали: 3500 – 2000 = 1500 см³

Можно решать подобные задачи более рациональным способом.

По закону Архимеда объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 9/12  исходного объема:

Ответ: 1500

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Ok