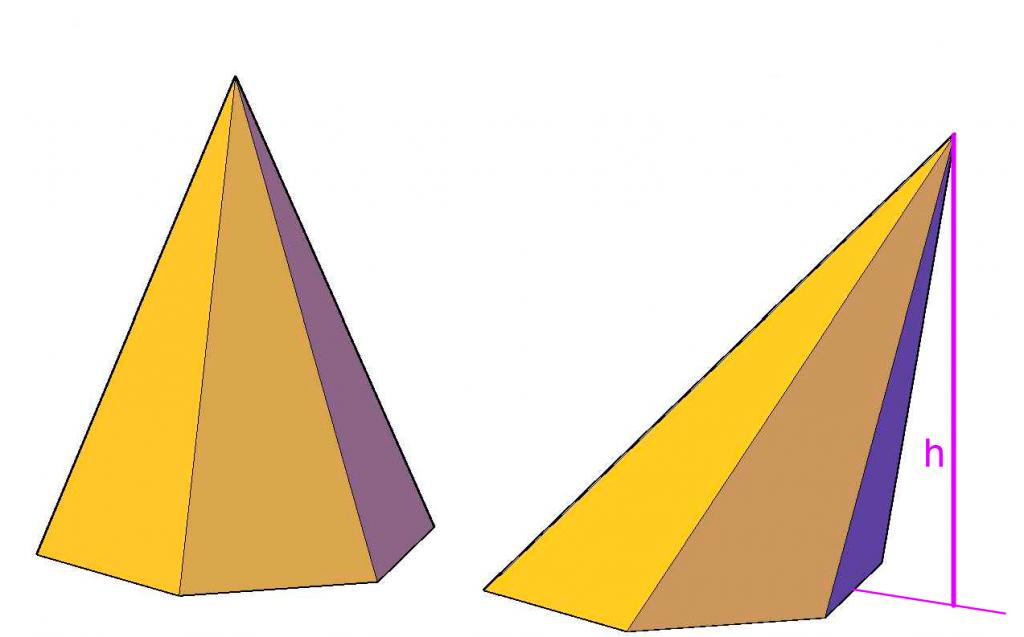
Основание правильной пирамиды является правильный многоугольник – равносторонний треугольник, квадрат. Основанием пирамиды называют ту фигуру, над которой расположена вершина пирамиды.То есть это та грань пирамиды, которая не включает в себя ее вершину. Площадь основания пирамиды – это площадь этой плоской фигуры.
Площадь основания правильной пирамиды
Правильная пирамида может быть трех видов:
- треугольная,
- четырехугольная,
- шестиугольная.
Соответственно у правильной треугольной пирамида основание – равносторонний треугольник. У правильной четырехугольной пирамиды основание – квадрат. В основании шестиугольной правильной пирамиды в основании лежит шестиугольник. Приведем формулы для нахождения площади основания пирамиды:
Площадь основания правильной треугольной пирамиды
В основании равносторонний треугольник – находим его площадь:
, где
– сторона треугольника.
Площадь основания правильной четырехугольной пирамиды
В основании правильной четырехугольной пирамиды лежит квадрат, площадь квадрата:
, где
– сторона квадрата.
Площадь основания правильной шестиугольной пирамиды
Это площадь правильного шестиугольника. Если известна сторона шестиугольника, то площадь правильного шестиугольника находится по формуле:
Площадь основания любой пирамиды
Площадь основания любой пирамиды – это площадь ее основания.
Если в основании пирамиды треугольник, то формулы для нахождения площади любого треугольника вы можете посмотреть в статье “Площадь треугольника”.
В основании пирамиды может лежать любой прямоугольник, любой многоугольник. Обычно в школьных задачах, в основании пирамиды часто лежит треугольник, редко прямоугольник. Задачи, в которых в основании пирамиды лежит пятиугольник, семиугольник или произвольных многоугольник, практически не встречаются. Хотя их можно увидеть в олимпиадных задачах.
Теперь давайте решим несколько задач для нахождения площади основания пирамиды
Примеры решения задач
Задача 1
Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.
Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона
, тогда
Ответ:
Задача 2
Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5 м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?
Решение:
Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны
. Получим:
м2.
Теперь подсчитаем, сколько нам понадобится досок: .
Ответ: 108 досок.
Задача 3
Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.
Решение: иными словами – нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой – высотой. Определяем площадь по формуле:
.
Ответ: 8
|
бонус за лучший ответ (выдан): 2 кредита Нужно найти длину одной стороны основания, а так как пирамида правильная — её грани это равнобедренные треугольники (эта информация может быть важна, так как мы не знаем точно какие длины катетов или величины углов в задачке) — а основание будет являться квадратом. Возводим длину известной стороны в квадрат (перемножаем саму на себя) и получаем площадь основания. автор вопроса выбрал этот ответ лучшим sergej1 10 лет назад Площадь квадрата S = a в квадрате, это через сторону S = 0.5 d в квадрате, это через диагональ, где a — сторона и d — диагональ Знаете ответ? |
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
1. Через длину основания (a) и высоту (h):
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник
Вычисление площадей фигур является одной из приоритетных задач геометрии на плоскости и в пространстве. В данной статье рассмотрим объемную фигуру пирамиду. И покажем, какие формулы площади основания пирамиды следует применять для вычисления этой величины.
Что представляет собой пирамида?
Ответ на этот вопрос не столь очевиден, как многим может показаться. Когда люди слышат слово «пирамида», то в их воображении всплывает великое каменное сооружение египетских фараонов. Однако это лишь частный случай фигур этого класса.

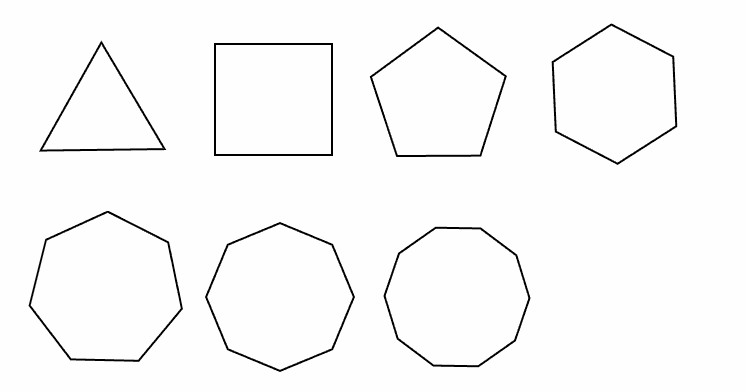
С точки зрения точной науки геометрии, пирамида является фигурой в пространстве, образованной n-угольником, каждая из вершин которого соединена с одной единственной точкой. Эта точка в плоскости n-угольника находиться не должна. Здесь n — целое число, равное количеству углов (сторон) плоского многоугольника. Для наглядного представления описанной фигуры приведем фотографию.

Здесь изображен набор самых разных пирамид. Верхняя левая называется треугольной, поскольку ее основание является треугольником. Нижняя правая пирамида называется двадцатиугольной.
Эта фотография позволяет сделать некоторые выводы, касающиеся пирамид. Во-первых, стороны, которые соединяют n-угольник с вершиной фигуры, представляют собой треугольники. Во-вторых, количество сторон любой пирамиды равно n+1 (один n-угольник и n треугольников), n-угольник называют основанием, а треугольники — боковыми гранями. В-третьих, можно заметить, что увеличение сторон основания приближает пирамиду по своей форме к конусу. Этот факт позволяет считать конус пирамидой с бесконечным числом боковых граней.
Правильные и неправильные фигуры
Мы выяснили, что такое основание фигуры. Тем не менее, до того как начать обсуждение формулы площади основания пирамиды, следует дать определение правильных и неправильных фигур этого класса.
Каждый школьник знает, что любой плоский многоугольник имеет геометрический центр. Если многоугольник изготовить из однородного материала, то геометрический центр совпадет с центром масс. Например, геометрический центр прямоугольника — это точка, где его диагонали пересекаются, для треугольника он находится в точке пересечения медиан. Концепция геометрического центра связана с понятиями правильной и неправильной пирамиды.
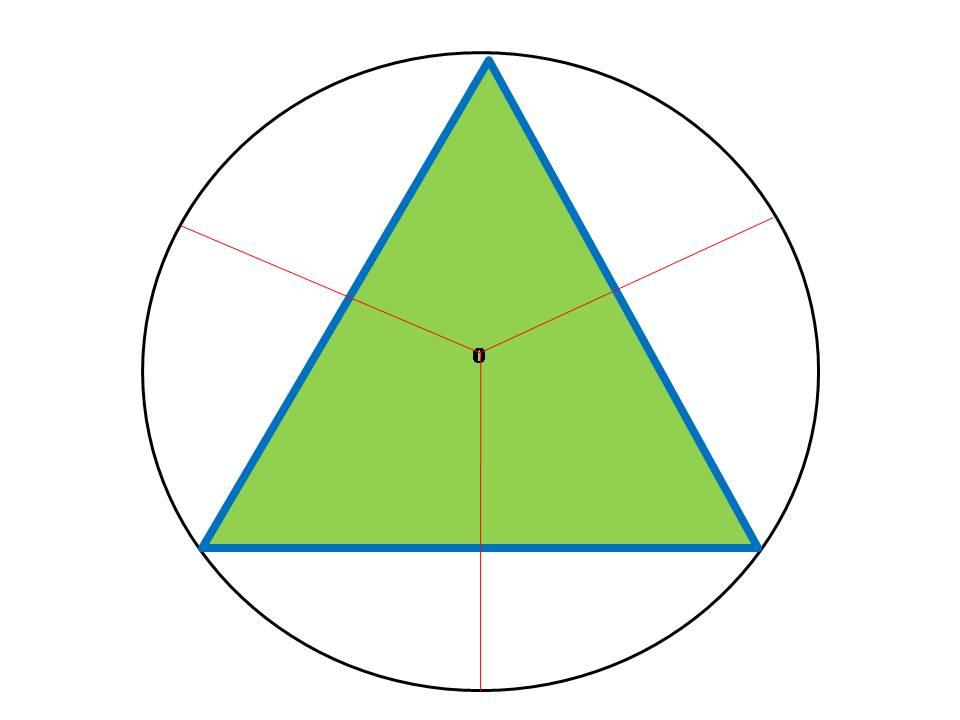
Выше было упомянуто о вершине пирамиды. Она соответствует точке, где пересекаются все треугольные боковые грани фигуры. Если из вершины опустить перпендикуляр к основанию, то длина полученного отрезка будет соответствовать расстоянию от вершины до основания. Этот отрезок называется высотой фигуры.
Если высота пересекает многоугольник в его геометрическом центре, то пирамида называется прямой. Если основанием прямой пирамиды будет многоугольник, имеющий стороны одинаковой длины и равные между собой углы, то пирамида называется правильной. Соответственно, если какое-либо из названных условий не выполняется, то говорят о неправильной пирамиде.

Согласно описанной классификации, пирамида Хеопса является правильной четырехугольной, имеющей в основании квадрат.
Площадь основания правильной пирамиды
Для вычисления площади основания пирамиды следует использовать соответствующие формулы для конкретного n-угольника. Например, в случае треугольника — это произведение высоты на основание, которое поделено пополам, в случае параллелограмма — это произведение стороны на опущенную на нее высоту.
Если n-угольник является правильным, то формула площади основания пирамиды будет универсальной. Запишем ее:
Sn = n/4*a2*ctg(pi/n)
Где параметр a — это длина стороны n-угольного основания. Эта формула справедлива независимо от того, рассматривается треугольная или стоугольная пирамида. Функцию котангенса следует вычислять с помощью калькулятора, однако для 3-, 4- и 6-угольника она имеет табличное значение.
Отметим, что данной формулой можно пользоваться, если основание пирамиды — это правильный многоугольник. Справедливость формулы не зависит от того, является пирамида прямой или наклонной.
Пирамида треугольная правильная
Равносторонний треугольник является основанием правильной пирамиды треугольной. Площадь основания ее можно определить, если применить записанную в пункте выше формулу для Sn. Учитывая, что n = 3, получаем:
S3 = n/4*a2*ctg(pi/n) = 3/4*a2*ctg(pi/3) = √3/4*a2
Зная длину основания a, можно рассчитать соответствующую площадь.
Любопытно отметить, что в треугольной пирамиде, которую часто называют тетраэдром, все четыре стороны являются треугольниками. В правильной фигуре в общем случае только одна из сторон представляет собой равносторонний треугольник (основание). Остальные грани являются треугольниками равнобедренными.
Четырехугольная пирамида правильная

Пожалуй, она является самой знаменитой среди класса пирамид. Формула для площади основания пирамиды четырехугольной правильной известна школьнику уже в начальных классах, поскольку речь идет о площади квадрата. Следуя общему подходу, воспользуемся выражением для Sn. Подставляя n = 4, получаем:
S4 = 4/4*a2*ctg(pi/4) = a2
Например, найдем площадь основания четырехугольной пирамиды Хеопса. Длина стороны ее основания составляет приблизительно 230 метров. Это означает, что соответствующая площадь равна 52,9 тыс. м2, что больше площади 10 футбольных полей.
Фигура пирамида с точки зрения геометрии состоит из различных элементов и описывается с помощью разных величин, например, длины ребер или высоты. Одной из важных характеристик этого класса фигур является площадь основания. В данной статье содержится ответ на вопрос, с помощью каких формул площадь основания пирамиды можно посчитать.
Пирамида как геометрическая фигура
Прежде чем говорить о конкретных формулах площади основания пирамиды, следует дать ясное определение этой фигуре и ее элементам. Пирамида — это геометрический объект в пространстве, который образован n+1 гранью, причем n граней — это треугольники, пересекающиеся в одной точке, и одна грань является n-угольным основанием.
Каркас из ребер пирамиды легко получить, если представить себе плоский многоугольник, вершины которого соединены отрезками с единственной пространственной точкой. Последняя не должна находиться в плоскости многоугольника. Эта точка является главной вершиной фигуры. Помимо нее, пирамида имеет еще n вершин, которые принадлежат основанию.
Основными линейными параметрами любой пирамиды являются длины ее ребер и высота. Сами ребра бывают двух типов: те, которые относятся к основанию, и те, что ограничивают боковые треугольные грани. Высотой пирамиды называется длина перпендикуляра, который опущен на основание с главной вершины. Если он пересекает основание в его центре, то говорят о прямой пирамиде. Если прямая пирамида имеет правильное основание, например, равносторонний треугольник, то ее называют правильной фигурой. С правильными пирамидами удобно работать при расчете геометрических свойств, например, площадей и объемов.
Как вычислить площадь основания?
Ввиду описанного выше многообразия пирамид, универсальной формулы площади основания фигуры не существует. Так, если в основании находится треугольник, то следует применять соответствующее выражение для расчета его площади, если это будет основание в виде параллелограмма, то формула уже будет иметь иной вид. Иными словами, для каждого n-угольника произвольной формы необходимо провести определенный геометрический анализ, чтобы определить его площадь.
Ситуация сильно упрощается, если основанием является равносторонний и равноугольный многоугольник. Отметим, что речь идет только о правильности самого основания, а не пирамиды в целом. Имея правильное основание, она может быть наклонной.
Для правильного основания существует выражение общего характера, которое позволяет вычислить его площадь. В случае n-угольника правильного формула площади основания пирамиды имеет следующий вид:
Sn = n/4*a2*ctg(pi/n).
Где a — длина ребра основания, n — количество сторон основания. Подставляя в эту формулу любое значение n и длину a стороны, мы можем получить площадь многоугольника, а значит, площадь основания пирамиды.
Основание треугольной правильной пирамиды
Правильная треугольная пирамида также называется тетраэдром. Состоит она из четырех треугольников, один из которых обязательно должен быть равносторонним. Он является основанием фигуры. Чтобы записать формулу площади основания пирамиды треугольной, можно поступить двумя способами. Опишем оба.
Как известно, высота в равностороннем треугольнике является его биссектрисой и делит угол в 60o пополам. Этот факт позволяет использовать тригонометрическую функцию, например, косинус, чтобы вычислить высоту треугольника. Обозначим ее ha, тогда ее длина определится так:
ha = a*cos(30o) = √3/2*a.
Тогда площадь основания треугольника равностороннего запишется как произведение ha на длину его стороны, деленное пополам:
S3 = 1/2*√3/2*a*a = √3/4*a2.
Второй способ, который также приводит к этой формуле, заключается в простой подстановке значение n=3 в приведенную выше формулу для Sn. В таком случае получаем:
S3 = 3/4*a2*ctg(pi/3) = 3/4*a2*1/√3 = √3/4*a2.
Основание четырехугольной правильной пирамиды
Типичным примером этой пирамиды являются древние каменные сооружения в Гизе, Египет. Основанием этих пирамид является квадрат. Каждый школьник знает, как рассчитать площадь квадрата, если длина его стороны известна. Соответствующая формула площади основания четырехугольной пирамиды имеет простой вид:
S4 = a2.
К этому выражению можно прийти, если подставить n=4 в равенство для Sn.
Для многих правильных оснований с n>4 нельзя точно записать формулу в том виде, в котором она записана для S3 и S4. Связано это с тем, что функция котангенса приводит к иррациональным числам, которые не могут быть записаны в виде конкретного корня.