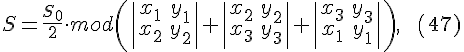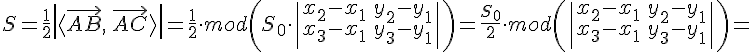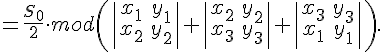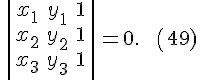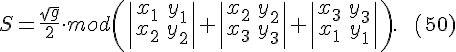В школьном курсе геометрии доказывается, что площадь ортогональной проекции многоугольника равна площади исходного многоугольника на косинус угла между плоскостями этих многоугольников… то есть
$%
S_{pr} = Scdotcosvarphi
$%
Вектор $%bar{n} = bar{a}times bar{b}$% имеет длину, равную площади параллелограмма, построенного на векторах $%bar{a}$% и $%bar{b}$%… Кроме того, вектор $%bar{n}$% перпендикулярен плоскости параллелограмма… а как известно, угол между нормалями равен углу между плоскостями, либо смежный с ним…
Итого,
$$
S_{pr} = |bar{n}|cdotfrac{|bar{n}cdotbar{c}|}{|bar{n}|cdot|bar{c}|} = frac{|(bar{a}times bar{b})cdotbar{c}|}{|bar{c}|}
$$
19
Фев 2014
Категория: Справочные материалы
Площадь ортогональной проекции многоугольника
2014-02-19
2014-02-19
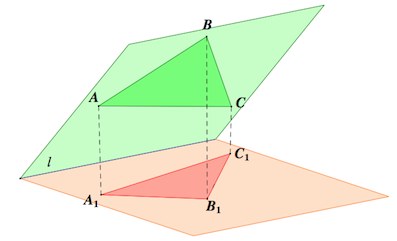
Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.
Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.
Доказательство:
Пусть треугольник – проекция треугольника
на проецируемую плоскость.
Докажем, что
,
где – угол между плоскостями
Для этого разобьем треугольник на два треугольника c общей стороной
, параллельной прямой
пересечения плоскостей
. (Частный случай, когда одна из сторон треугольника
параллельна линии пересечения плоскостей
, можно рассмотреть отдельно (самостоятельно)).
Проекция треугольника – треугольник
. Причем
.
Пусть – перпендикуляр к
. Тогда по т. о трех перпендикулярах и
– перпендикуляр к
. Стало быть,
– угол между плоскостями треугольников (проецируемого и проекции).
Пусть – точка пересечения
и
,
– проекция т.
на плоскость
. Очевидно,
– высота треугольника
(
– высота треугольника
).
Из треугольника
Но и
Тогда
Имеем:
Аналогичные рассуждения – для пары треугольников и
:
(где – высота треугольника
,
– ее проекция)
Итак, суммируя площади треугольников и
соответственно, получаем
или
Что и требовалось доказать.
Пример.
Ребро куба равно 2 см. Через диагональ основания под углом к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.
Решение:
Пусть плоскость сечения проведена через диагональ и пересекает боковое ребро (
) в точке
.
По вышеуказанной теореме
где треугольник – проекция треугольника
на плоскость основания,
– угол между плоскостями
Ответ:
Применение теоремы можно также посмотреть, например, в этой задаче.
Автор: egeMax |
Нет комментариев
Печать страницы
Определение
25.1. Пусть и
два
вектора, параллельные некоторой
ориентированной плоскости
(ориентация
определяется некоторым
базисом ).
Площадью
ориентированного параллелограмма ,
построенного на векторах и
называется
число ,
определяемое следующим образом:
1. ,
если базис положительно
ориентирован;
2. ,
если базис отрицательно
ориентирован;
3. ,
если векторы и
коллинеарны.
Очевидно,
что .
Пусть будет
единичный вектор, перпендикулярный
нашей плоскости и направленный в ту
сторону, с которой мы смотрим на нее;
тогда .
Если тройка векторов правая,
то и
параллелограмм ориентирован
положительно, т.е .
Если тройка векторов левая,
то и
параллелограмм ориентирован
отрицательно, т.е .
В том и другом случае
Из
этого легко усмотреть следующие свойства
ориентированной площади
1. .
2. .
3. .
4. .
Зададим
теперь векторы и
их
координатами относительно базиса :
Тогда
В
силу свойств ориентированной площади
получаем
Учитывая,
что и
,
получим
Обозначим
через ,
т.е. площадь параллелограмма, построенного
на базисных векторах. Тогда получаем,
что
Пусть
теперь на плоскости задана аффинная
система координат .
ТЕОРЕМА
25.1. Площадь треугольника
,
заданного своими вершинами относительно
аффинной системы координат на
плоскости вычисляется по формуле
( — знак
модуля или абсолютной величины)
Доказательство. Из
предыдущих рассуждений следует, что .
Поскольку (см.
формулу ),
то с учетом получаем
ТЕОРЕМА
25.2. Для
того чтобы три точки относительно
аффинной системы координат ,
принадлежали одной прямой, необходимо
и достаточно, чтобы выполнялось равенство
или
Замечание
25.1. Если
заданы метрические коэффициенты базиса
,
входящего в систему координат ,
то площадь ,
как легко видеть, вычисляется по
формуле ,
где .
Поэтому формулу можно
записать в виде
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
30.03.201527.55 Mб32Административное право России Конин Н.М..pdf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Описание презентации по отдельным слайдам:
-
1 слайд
Проекции
геометрических фигур
на плоскость
Маланичева Марина Владиславовна
Финансово-экономическая школа
Г. Москва -
2 слайд
Проекция
точки на плоскость
α
А
О
Основание перпендикуляра
Точка не лежит
в плоскости
АО – перпендикуляр, опущенный из точки А на плоскость α
Точка О – проекция точки А
на плоскость α
2) Точка лежит
в плоскости
α
А
Проекция точки А на плоскость α совпадает с точкой А
Проекция точки А
на плоскость α, полученная с помощью перпендикуляра, опущенного из точки А на эту плоскость называется ОРТОГОНАЛЬНОЙ проекцией -
3 слайд
Проекции
геометрических фигур
на плоскость
Ортогональные проекции каждой точки отрезка АВ на данную плоскость,
образует отрезок, который является
ОРТОГОНОАЛЬНОЙ ПРОЕКЦИЕЙ отрезка АВ на эту плоскость.
А
В
α
А1
В1
С
С1
Точка А1 –ортогональная проекция точки А на плоскость α
Точка В1 –ортогональная проекция точки В на плоскость α
Точка С1 –ортогональная проекция
произвольной точки С на плоскость α
Отрезок А1В1 –ортогональная проекция
Отрезка АВ на плоскость α -
4 слайд
Геометрическая фигура,
полученная с помощью ортогональной проекции
каждой её точки
на данную плоскость,
является
ОРТОГОНОАЛЬНОЙ ПРОЕКЦИЕЙ данной геометрической фигуры на эту плоскость. -
5 слайд
Точка А не лежит в плоскости α
Постройте ортогональную проекцию данной геометрической фигуры на плоскость
1.
α
А
В
С
А1
Построим её ортогональную проекцию на плоскость α – точку А1
Точки В и С лежат в плоскости α
Они проектируются сами в себя
Построим проекцию отрезка АВ на плоскость α – отрезок А1В
Проекцией отрезка АС на плоскость α будет отрезок А1С
Проекция отрезка ВС на плоскость α будет совпадать с отрезком ВС
Проекцией треугольника АВС на плоскость α будет треугольник А1ВС
Практическая работа -
6 слайд
2. Постройте ортогональную проекцию параллелограмма АВСD на плоскость α
А
В
С
D
α -
7 слайд
С
B
А
α
β
3. Постройте ортогональную проекцию треугольника АВС на плоскость α -
8 слайд
α
β
А
В
С
4. Постройте ортогональную проекцию треугольника АВС на плоскость α, если он лежит в плоскости β, параллельной плоскости α -
9 слайд
3. Постройте ортогональную проекцию треугольника АВС на плоскость α, если треугольник лежит в плоскости, перпендикулярной к плоскости α
α
β
А
В
С -
10 слайд
Понаблюдаем и сделаем выводы
1. Всегда ли ортогональная проекция геометрической фигуры является геометрической фигурой такого же вида?
2. Всегда ли ортогональная проекция геометрической фигуры является геометрической фигурой, равной исходной?
3. Когда ортогональная проекция геометрической фигуры является
геометрической фигурой, равной исходной?
Может ли ортогональной проекцией многоугольника быть отрезок?
5. Когда ортогональной проекцией многоугольника будет являться отрезок?
6. Может ли ортогональной проекцией многоугольника быть одна точка? -
11 слайд
Площадь ортогональной проекции данной геометрической фигуры на плоскость
α
А
В
С
А1
Треугольник А1ВС – ортогональная проекция
треугольника АВС на плоскость α
Найдём площадь треугольника А1ВС
1. Построим высоту А1Н треугольника А1ВС
Н
3. Проведём наклонную АН
Тогда по теореме о трёх перпендикулярах
наклонная АН перпендикулярна ВС
2. 𝑺= А1Н∙ВС 𝟐
4. Угол АНА1 – линейный угол двугранного угла между плоскостью треугольника АВС и плоскостью α
5. Рассмотрим треугольник АА1Н – прямоугольный.
А1Н =АНсоsАНА1
𝑺= 𝑨𝑯∙𝒄𝒐𝒔𝑨𝑯𝑨1∙𝑩𝑪 𝟐
𝑺= 𝑨𝑯∙𝑩𝑪∙𝒄𝒐𝒔𝑨𝑯𝑨1 𝟐
S = SABC · cosАНА1 -
12 слайд
Теорема:
Площадь ортогональной проекции фигуры на плоскость
равна произведению площади данной фигуры и косинуса угла между плоскостью исходной фигуры и плоскости её проекции
Sпроекции = Sф · cosψ
α
А
В
С
А1
ψ -
13 слайд
Применение теоремы о площади ортогональной проекции геометрической фигуры
Задание:Используя чертежи из практической работы,
найдите площадь ортогональной проекции
данных геометрических фигур при следующих дополнительных условиях:
Треугольник АВС-равнобедренный; АВ=ВС=10см, АС=12см; двугранный угол ((АВС);α) =60ᵒ.2. АВСD- ромб со стороной 5см, АС =8см; расстояния от точек В и D до плоскости α равно 3см, а от точки С до плоскости α — 6см.
Четырехугольник и вектор на плоскости
Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:
- ее противоположные стороны и углы равны друг другу;
- сумма всех четырех углов составляет 360 градусов;
- если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
- любая диагональ делит фигуру на две равные части (треугольники);
- пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
- любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.
Специальные типы
Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:
- Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
- Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
- Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).
Направленные отрезки и операция умножения
Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:
P (x1, y1); Q (x2, y2).
Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:
PQ- = Q — P = (x2-x1, y2-y1).
Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.
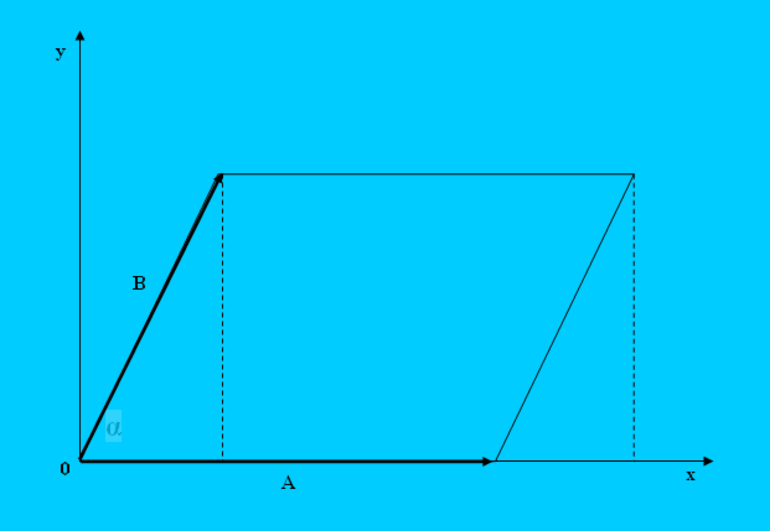
Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:
c- = [a-*b-] = |a-|*|b-|*sin (alfa).
Здесь alfa — угол между a- и b-, а |a-| и |b-| — длины соответствующих направленных отрезков.
Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.
Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:
c- = (0, 0, (a1*b2-b1*a2)).
Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.
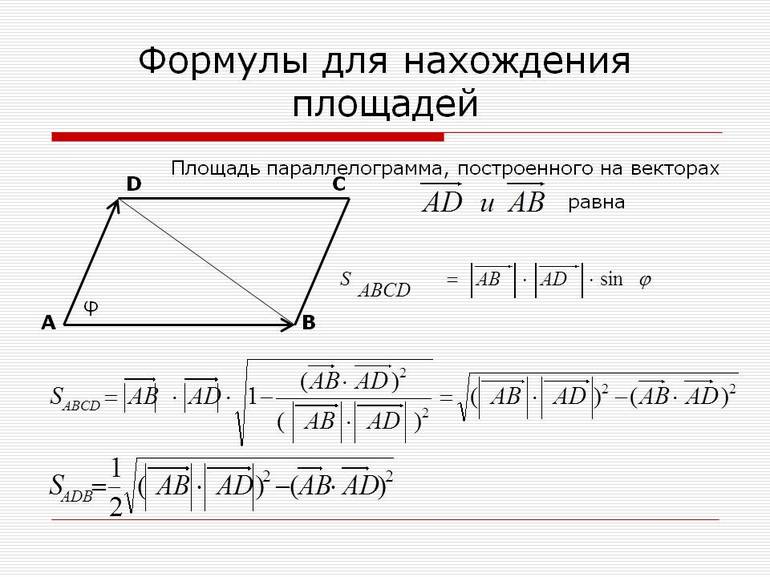
Формула площади из геометрии
Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:
S3 = ½*h*a.
Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:
S4 = 2*S3 = h*a.
Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:
sin (alfa) = h/b => h = b*sin (alfa).
Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:
S4 = a*b*sin (alfa).
Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.
Построение параллелограмма
Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.
Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:
S4 = a*b*sin (alfa) = |[a-*b-]|.
Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:
S4 = |(a1*b2-b1*a2)|.
Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.
Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.
Задача с тремя точками
Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:
- A (1,-1);
- B (2, 0);
- C (-4, 3).
На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.
Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:
AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).
Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:
S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.
Результат получен в единицах квадратных соответствующей двумерной системы координат.
Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.
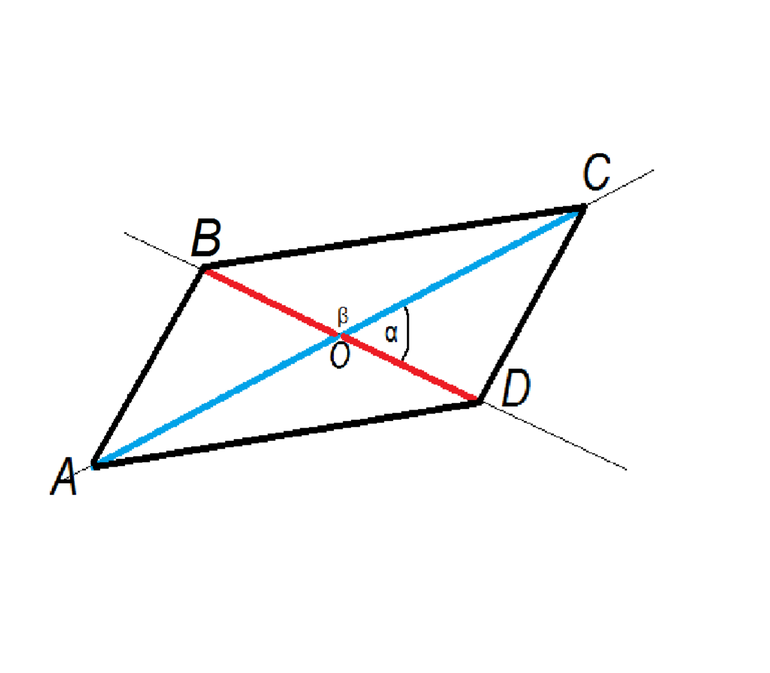
Диагонали фигуры
Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.
Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:
S4 = [a-*f-] = |a-|*|f-|*sin (beta).
Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:
S4 = ½*|[e-*f-]| = ½*|e-|*|f-|*sin (teta).
Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.
Пример решения
Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:
e- = (2, -1); f- = (1, -4).
Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:
S4 = ½*|[e-*f-]| = ½*|-8+1| = 3,5.
В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.
Трехмерное пространство
В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.
Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.