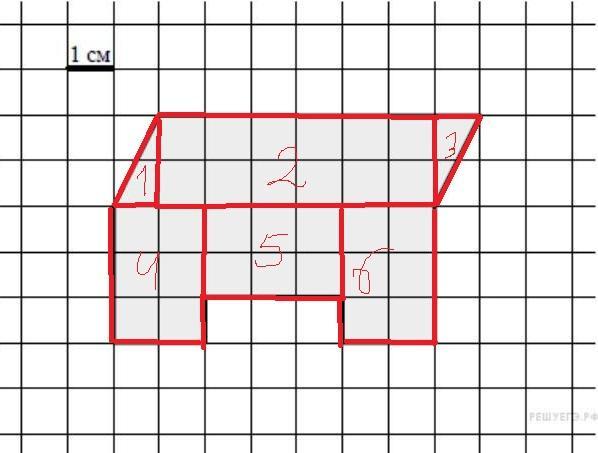
Способ 1. разбиваем фигуру на геометрические фигуры и складываем площади
S=S1+S2+S3+S4+S5+S6= 1*2*0,5+6*2+1*2*0,5+3*2+2*3+2*3=32см
Способ 2. ищем общую площадь и вычитаем из нее площади оставшихся кусков
S= Sобщ-S1-S2-S3-S4= 5*8-1*2*0,5-1*2*0,5-1*3-1*3= 32см
Довольно точно можно вычислить площадь прямоугольной фигуры, но для фигуры неправильной формы можно найти её приближённую площадь. Для этого удобно использовать палетку.
Палетка — это прозрачная плёнка (или калька), расчерченная на равные квадраты со стороной (1) см.
Самостоятельно сделай палетку.
С её помощью ты сможешь быстро находить приближённую площадь разных фигур.
Для нахождения приближённой площади фигуры нужно:
1) наложить палетку на фигуру;
2) посчитать число (a) целых клеток внутри фигуры;
3) посчитать количество (b) клеток, частично входящих в фигуру;
4) вычислить приближённую площадь
S≈a+b:2
.
Поясним также, зачем нужно делить (b) на два.
(b) — число клеток, частично входящих в фигуру. У одних большая часть входит в фигуру, у других — меньшая. Из них можно составить приближённо (b:2) полных клеток (если (b) нечётно, то можно сначала увеличить (b) на (1), а потом уже разделить на (2)).
Обрати внимание!
Для записи приближённого равенства используется знак
≈
.
Найдём с помощью палетки приближённую площадь фигуры (B) неправильной формы.
1. Наложим палетку на фигуру (B).
2. Посчитаем количество (a) клеток, целиком находящихся внутри фигуры (закрашены зелёным цветом):
3. Посчитаем количество (b) клеток, частично входящих в фигуру (B) (закрашены синим). Таких клеток (17) — это нечётное число, поэтому увеличим это число на (1) и поделим на (2):
17+1=18,18:2≈9.
4. Сложим числа, полученные в пунктах (2) и (3), и запишем приближённую площадь фигуры (B):
S≈16+9=25см2.
Обрати внимание!
Нужно понимать разницу между оценкой площади и нахождением её приближённого значения!
Оценка площади записывается неравенством
a<S<b
.
Приближённое значение площади — это число, которое можно найти по формуле
S≈a+b:2
.
Источники:
Изображение: палетка. © ЯКласс.
Изображения: фигура. © ЯКласс.
Как найти площадь неправильной фигуры
В школьном курсе геометрии ученики в основном считают площади правильных многоугольников. Между тем, для решения множества практических задач нередко приходится иметь дело с неправильными геометрическими фигурами. С этой проблемой человек сталкивается и при определении размеров дачного участка или придомовой территории, и при расчете количества ткани для шитья, и еще во многих случаях. Высчитать площадь неправильной фигуры можно несколькими способами.

Вам понадобится
- — неправильная геометрическая фигура;
- — измерительные инструменты;
- — прозрачный пластик;
- — линейка;
- — угольник;
- — шариковая ручка.
Инструкция
Рассмотрите геометрическую фигуру и определите, какие ее параметры вам известны. Это могут быть длины сторон или углы. В зависимости от заданных параметров и выберите способ определения площади. Например, разделите ее на несколько фигур, формулы вычисления площади которых вы знаете. Один из самых распространенных методов — провести диагонали из одного угла ко всем остальным вершинам. В этом случае вам нужно знать формулу вычисления площади произвольного треугольника. Но никто не запрещает разделить заданную фигуру и на другие многоугольники. Например, при расчете площади пола в комнате с нишей удобнее разделить неправильную фигуру на два прямоугольника или квадрата.
Для определения площади не слишком большой детали можно воспользуйтесь палеткой. Ее можно сделать самому. Отрежьте прямоугольный кусок любого прозрачного пластика. Разделите его на квадраты, площадь которых вам известна — например, 1х1 или 0,5х0,5 см. Линейка и угольник должны быть точными. Наложите палетку на деталь. Сосчитайте полные квадратики, затем — неполные. Количество неполных квадратов разделите на 2 и приплюсуйте результат к числу целых. Чем мельче деления на палетке — тем точнее будет результат. Аналогично можно посчитать и площадь участка. Роль палетки будет выполнять сетка из квадратов со стороной 1х1 м, начерченная на земле или отмеченная колышками с протянутыми между ними шнурами. Можно ограничиться и разметкой территории на полосы. .
С крупными площадями можно поступить и иначе. Возьмите максимально точный план участка или придомовой территории. Определите масштаб. Воспользуйтесь одним из предложенных способов. Затем полученное количество квадратных сантиметров переведите в нужный масштаб.
Полезный совет
При изготовлении плоских деталей из металла можно вычислить их площадь по эталону с помощью взвешивания. Вырежьте саму деталь и эталон — квадратик, площадь которого удобно рассчитать. Делать их необходимо из одного и того же материала, причем толщина листа должна быть одинаковой и при этом незначительной. Вычислите соотношение масс, а по ней — неизвестную площадь. Однако это не очень точный способ и применять его можно только в крайних случаях.
Любую неправильную фигуру можно представить в виде графика. Каждая точка имеет свои координаты. Представьте каждый отрезок как график функции. Площадь участка от абсциссы до него являет собой определенный интеграл. Высчитайте все интегралы. Площадь фигуры определите с помощью разности интегралов с большим и меньшим значением. Это довольно трудоемкий метод, но он дает наибольшую точность.
Источники:
- http://matemonline.com/rubrika/%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB/
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
In this platform, you have to learn about how to find the Perimeter and Area of irregular figures. An irregular shape will be of any size and length. We will see irregular shapes all around us, for example, a diamond shape, a kite, a leaf, a flower, etc. The Area of irregular shapes will be the space occupied by the shape which is measured in square units. The Perimeter of irregular shapes is by adding all the lengths of their sides. Any shape whose sides and angles are not of equal length is named an irregular shape.
On this page, you will learn about the definition of the area and the perimeter of irregular figures, how to find the area and perimeter of irregular figures, some solved example problems, and so on.
Read More:
- Area and Perimeter of Combined Figures
- Area of a Circular Ring
- Worksheet on Area of the Path
Irregular Figures – Definition
The Irregular Figures are defined as a figure that is not a standard geometric shape. An irregular shape is simply a shape where every single side is not the same length. But some irregular figures are made up of two or further standard geometric shapes. If the shape is irregular then it has some angles that are not all the same size. Based on the number of sides or corners we can decide that irregular figure.
How to find Perimeter and Area of Irregular Figures?
The following are the ways for finding the area and perimeter of irregular figures:
How to find Area of Irregular Shapes or Figures?
- Step 1: First, divide the compound shape into a basic regular shape.
- Step 2: Next, find each basic shape area separately.
- Step 3: Now Add all the areas of basic shapes together.
- Step 4: Now, write the final answer in square units.
How to find the Perimeter of Irregular Figures?
To find the perimeter of the irregular figure, we can simply add up each of its outer sides length of a shape. To find the perimeter of any shape like rectangle, square, and so on you have to add all the lengths of four sides. Consider ‘A’ is in this case the length of the rectangle and ‘B’ is the width of the rectangle.
See More:
- Plane Figures
- Solid Figures
- Rectilinear Figures
Perimeter and Area of Irregular Shapes Examples
Example 1:
The Irregular Figure is given below. Find the area of that figure?
Solution:
As given in the question, the irregular figure is given.
Now, we can break the given irregular figure. After separating the figure we have two rectangle blocks.
Next, we will find the area of those two rectangles. The area of the irregular figure is the sum of the areas of two rectangles.
The width of one block is 12 and the length of the block is 4.
Next, the width of the other rectangle is 2, but its length is not given. By using the upper rectangle length we can find the length of the lower rectangle. So the right side of the figure is the length of the upper rectangle block plus the length of the lower rectangle block.
Since the total length is 10 units, the right side of the upper rectangle is 4 units long. So the length of the lower rectangle will be 6 units.
So the area of the figure is,
The Area of the figure is the Area of the upper rectangle + Area of the lower rectangle
We know that the Area of the rectangle is, length x width (or) breadth.
So, the area of a figure is , lw + lw = 12(4) + 2(6).
Area of the figure is = 48 + 12 = 60sq.units.
Thus, the total area of the figure is 60 square units.
Example 2:
Find the area of the below-given irregular figure?
Solution:
As given in the question, the given figure is an irregular figure.
Now, we can break the given irregular figure. After separating the figure, we have two blocks one is a triangle block and another one is a rectangle.
Next, we will find the area of the irregular figure. The area of the irregular figure is the sum of the areas of two rectangles.
The rectangle has a length of 8 units and a width of 4 units. We need to find the base and height of the triangle.
On both sides of the rectangle 4units, the perpendicular side of the triangle is 3 units, which is 7- 4 = 3units.
Next, the length of the rectangle is 8units, so the base of the triangle is 3units, which is 8-5= 4units.
Now, we can add the areas then we get the area of the irregular figure.
So, the Area of the figure is the Area of the rectangle + the Area of the triangle.
We know the formulas, the area of the rectangle is, length x width (or) breadth.
The area of the triangle is 1/2bh.
So, the area of a figure is , lw + 1/2bh = 8(4) + 1/2(3)(3).
Area of the figure is = 32 + 4.5 = 36.5sq.units.
Hence, the total area of the given irregular figure is 36.5square units.
Example 3:
The figure is given below. Find the perimeter of the given Pentagon figure?
Solution:
As given in the question, the irregular shape figure is given.
This shape is a pentagon because it has five sides. Even though two of its sides are both 13m, it is an irregular pentagon because not all of its sides are the same length.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up the five side lengths.
We make the calculation easier by starting with the largest sides and also looking for number bonds to ten.
The two largest sides are 13m and 13m. These add together to make 26m.
The remaining three sides are 2m, 8m, and 9m. Now the value is 2m + 8m+ 9m = 19m.
Now, adding those two values are, 26m + 19m = 45m.
Thus, the perimeter of this given irregular pentagon is 45m.
Example 4:
Find the perimeter of the below-given figure?
Solution:
As given in the question, the figure is an irregular figure.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up all side lengths.
We make the mathematics easier by starting with the largest sides and also looking for number bonds to ten.
The largest sides is 10 cm. The remaining sides are 2cm, 2cm, 8cm, 8cm and 4 cm. Then the value is 2 cm + 2cm + 8 cm+ 8 cm + 4cm= 24cm.
Now, adding those two values are, 10 cm + 24 cm = 34 cm.
Thus, the perimeter of this given irregular figure is 34 cm.
FAQ’s on Perimeter and Area of Irregular Figures
1. What is meant by Irregular Figures?
An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or further standard geometric shapes.
2. Define Area of Irregular Figures?
The area of irregular shapes is defined as the quantity of space that is covered by an irregular shape. Irregular shapes are those shapes that do not have equal sides or equal angles. The unit for the area of an irregular shape is expressed in terms of square units, for representative, m2, cm2, in2, or feet2.
3. How to find the perimeter of Irregular Figures?
In order to calculate the perimeter of an irregular polygon we use the following two steps:
- Step 1: Note the length of each side of the given polygon.
- Step 2: Once the length of all the sides is acquired, then the perimeter is adding all the sides length.
Совет 1: Как обнаружить площадь неправильной фигуры
В школьном курсе геометрии ученики в основном считают площади положительных многоугольников. Между тем, для решения множества фактических задач неоднократно доводится иметь дело с неправильными геометрическими фигурами. С этой задачей человек сталкивается и при определении размеров дачного участка либо придомовой территории, и при расчете числа ткани для шитья, и еще во многих случаях. Высчитать площадь неправильной фигуры дозволено несколькими методами.
Вам понадобится
- – неправильная геометрическая фигура;
- – измерительные инструменты;
- – прозрачный пластик;
- – линейка;
- – угольник;
- – шариковая ручка.
Инструкция
1. Разглядите геометрическую фигуру и определите, какие ее параметры вам вестимы. Это могут быть длины сторон либо углы. В зависимости от заданных параметров и выберите метод определения площади. Скажем, поделите ее на несколько фигур, формулы вычисления площади которых вы знаете. Один из самых распространенных способов — провести диагонали из одного угла ко каждым остальным вершинам. В этом случае вам необходимо знать формулу вычисления площади произвольного треугольника. Но никто не воспрещает поделить заданную фигуру и на другие многоугольники. Скажем, при расчете площади пола в комнате с нишей комфортнее поделить неправильную фигуру на два прямоугольника либо квадрата.
2. Для определения площади не слишком огромный детали дозволено воспользуйтесь палеткой. Ее дозволено сделать самому. Отрежьте прямоугольный кусок всякого прозрачного пластика. Поделите его на квадраты, площадь которых вам вестима — скажем, 1х1 либо 0,5х0,5 см. Линейка и угольник обязаны быть точными. Наложите палетку на деталь. Сосчитайте полные квадратики, после этого — неполные. Число неполных квадратов поделите на 2 и приплюсуйте итог к числу целых. Чем мельче деления на палетке — тем вернее будет итог. Подобно дозволено посчитать и площадь участка. Роль палетки будет исполнять сетка из квадратов со стороной 1х1 м, начерченная на земле либо подмеченная колышками с протянутыми между ними шнурами. Дозволено ограничиться и разметкой территории на полосы. .
3. С большими площадями дозволено поступить и напротив. Возьмите максимально точный план участка либо придомовой территории. Определите масштаб. Воспользуйтесь одним из предложенных методов. После этого полученное число квадратных сантиметров переведите в надобный масштаб.
Совет 2: Как обнаружить площадь пола
Перед тем как начинать ремонт пола в доме, нужно узнать всеобщую площадь , дабы верно рассчитать число материала. Несложная, казалось бы, задача на деле может вызвать много сложностей. Дабы положительно обнаружить площадь пола , вам нужно знать некоторые нюансы измерительной науки.
Вам понадобится
- – рулетка;
- – электронный дальномер;
- – лист бумаги и карандаш;
- – калькулятор.
Инструкция
1. Если вам необходима всеобщая площадь квартиры либо отдельной комнаты, легко прочтите технический паспорт на квартиру либо дом, там указан метраж всякого помещения и всеобщий метраж квартиры.
2. Для измерения площади прямоугольной либо квадратной комнаты возьмите рулетку либо электронный дальномер и измерьте длину стен. При измерении расстояний дальномером непременно следите за перпендикулярностью направления луча, напротив итоги замеров могут быть искажены.
3. После этого полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадь ю пола , она измеряется в квадратных метрах.
4. Если требуется посчитать площадь пола больше трудной конструкции, скажем, пятиугольной комнаты либо комнаты с круглой аркой, схематично начертите эскиз на листе бумаги. После этого поделите трудную форму на несколько примитивных, скажем, на квадрат и треугольник либо прямоугольник и полукруг. Измерьте при помощи рулетки либо дальномера величину всех сторон получившихся фигур (для круга нужно узнать диаметр) и внесите итоги на ваш чертеж.
5. Сейчас посчитайте площадь всякой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр поделите попола м и возведите в квадрат (умножьте его на самого себя), после этого умножьте полученное значение на 3,14. Если вам надобна только половина круга, поделите полученную площадь попола м. Дабы рассчитать площадь треугольника, обнаружьте Р, для этого сумму всех сторон поделите на 2. После этого высчитайте число Р(Р-а)(Р-b)(Р-с) и извлеките из него квадратный корень. Полученное значение и будет площадь ю треугольника. Сложите площади всех примитивных фигур, из которых состоит ваша комната.
6. Если в полу есть отверстия, люки, углубления, бассейны, выступы и колонны, то их размер вычтите из площади пола . Для этого измерьте отдельно площадь всякого элемента, подметьте на вашей схеме и вычтите из всеобщего значения.
Полезный совет
Обратите внимание, что для подсчета числа материалов изредка неудовлетворительно примитивно узнать площадь пола. Для соблюдения симметричности рисунка покрытия, при специальной форме пола нужен больше трудный расчет, в итоге которого у вас останется много отходов.
Полезный совет
При изготовлении плоских деталей из металла дозволено вычислить их площадь по стандарту с подмогой взвешивания. Вырежьте саму деталь и стандарт — квадратик, площадь которого комфортно рассчитать. Делать их нужно из одного и того же материала, причем толщина листа должна быть идентичной и при этом незначительной. Вычислите соотношение масс, а по ней — незнакомую площадь. Впрочем это не дюже точный метод и использовать его дозволено только в крайних случаях. Всякую неправильную фигуру дозволено представить в виде графика. Всякая точка имеет свои координаты. Представьте весь отрезок как график функции. Площадь участка от абсциссы до него являет собой определенный интеграл. Высчитайте все интегралы. Площадь фигуры определите с подмогой разности интегралов с огромным и меньшим значением. Это достаточно трудоемкий способ, но он дает крупнейшую точность.