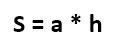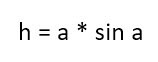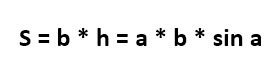Как рассчитать площадь параллелограмма
На данной странице калькулятор поможет рассчитать площадь параллелограмма онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Через основание и высоту
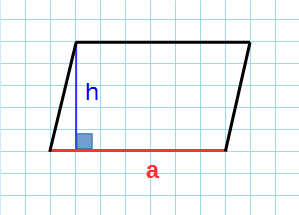
Формула для нахождения площади параллелограмма через основание и высоту:
a — длина основания; h — высота.
Через основания и угол между ними
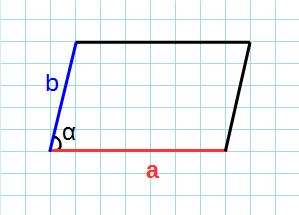
Формула для нахождения площади параллелограмма через основания и угол между ними:
a, b — длина основания; α — угол между основаниями.
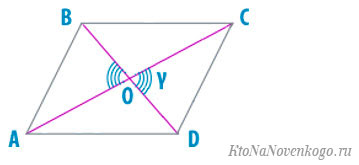
Через диагонали и угол между ними
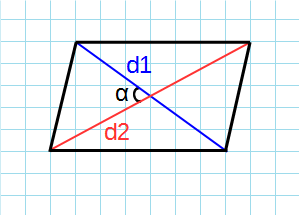
Формула для нахождения площади параллелограмма через диаганали и угол между ними:
d1, d2 — диагонали; α — угол между диагоналями.
Многоугольником считается фигура,имеющая количество сторон больше или равное 3.
1)Площадь треугольника со сторонами a,b,c, и высотами h1,h2,h3,
площадь S =a*h1/2=b*h2/2=c*h3/2,
или по формуле Герона :
S= V p*(p-a)*(p-b)*(p-c),
где p — полупериметр.
Площадь четырехугольника:
1)площадь квадрата :S = a^2,
2)площадь прямоугольника :S = a *b,
3)площадь параллелограмма : S =a * h1 = b *h2,
4)площадь ромба S = a *h =d1*d2,
где a,b -стороны четырёхугольника,h1,h2-высоты,d1,d2-диагонали ромба.
5)площадь произвольного четырёхугольника определяется путем разбивки его по диагонали и нахождения площади каждого треугольника отдельно.
Площадь правильного многоугольника равна произведению полупериметра =n*a,на апофему h
S=(n*a)*h/2
где а-сторона многоугольника,n-число сторон,h-апофема.
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.
Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит вот так:
Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.
И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
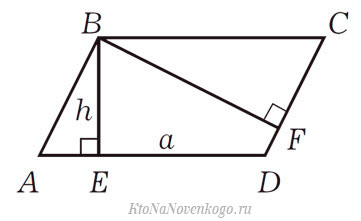
Как найти площадь параллелограмма, если известны сторона и высота
Возьмем для примера такой параллелограмм:
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
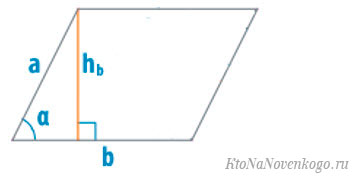
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
Соответственно, чтобы посчитать значение высоты надо:
И наша конечная формула для расчета площади будет выглядеть следующим образом:
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.
Каким способом считать:
Через сторону и высоту
Через стороны и угол
Через диагонали и угол между ними
Укажите размеры:
Результат:
Решение:
Ссылка на страницу с результатом:
# Теория
Параллелограмм — это четырёхугольник у которого противоположные стороны параллельны.
У параллелограмма противоположные стороны и противоположные углы равны.
Высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону.
Высотой параллелограмма также называют длину этого перпендикуляра. Расстояние между противоположными сторонами параллелограмма равно высоте параллелограмма.
Формулы площади параллелограмма
Площадь параллелограмма через сторону и высоту
a
h
a
S = a cdot h_a
- S — площадь параллелограмма
- a — сторона
- h — высота опущенная на сторону a
b
h
b
S = b cdot h_b
- S — площадь параллелограмма
- a — сторона
- h — высота опущенная на сторону b
Площадь параллелограмма через стороны и углы
a
b
α
β
S = a cdot b cdot sin alpha
S = a cdot b cdot sin beta
- S — площадь параллелограмма
- a, b — противоположные стороны параллелограмма
- α, β — углы между диагоналями (в градусах)
Площадь параллелограмма через диагонали и угол между ними
d
D
α
β
S = dfrac{1}{2} cdot D cdot d cdot sin alpha
S = dfrac{1}{2} cdot D cdot d cdot sin beta
- S — площадь параллелограмма
- D — большая диагональ параллелограмма
- d — меньшая диагональ параллелограмма
- α, β — углы между диагоналями (в градусах)
Войдите чтобы писать комментарии
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α, β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, (S):
Калькулятор — вычислить, найти площадь параллелограмма:
a(сторона)=
b(сторона)=
α или β (угол в градусах)= ( sin α=sin β )
S=
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d —меньшая диагональ
α, β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
Калькулятор — вычислить, найти площадь параллелограмма:
D (большая диагональ)=
d (меньшая диагональ )=
α или β (угол в градусах)= ( sin α=sin β )
S=
Формулы для параллелограмма:
Как найти стороны параллелограмма
Как найти диагонали параллелограмма
Острый угол и тупой угол параллелограмма
Углы между диагоналями параллелограмма
Формула суммы квадратов диагоналей параллелограмма
Высота параллелограмма и угол пересечения высот
Свойства и длина биссектрисы параллелограмма
Периметр параллелограмма
Все формулы по геометрии