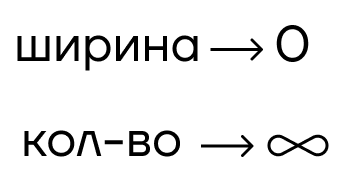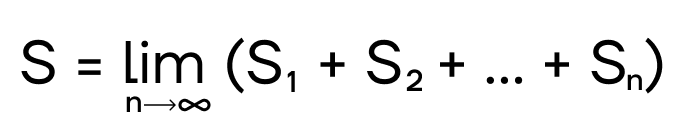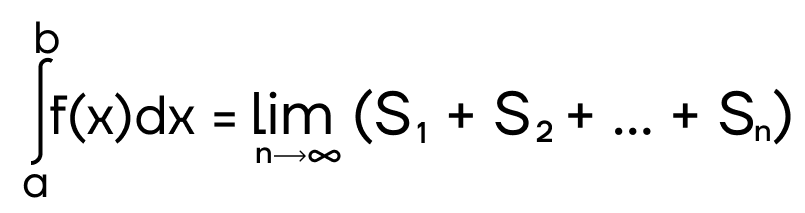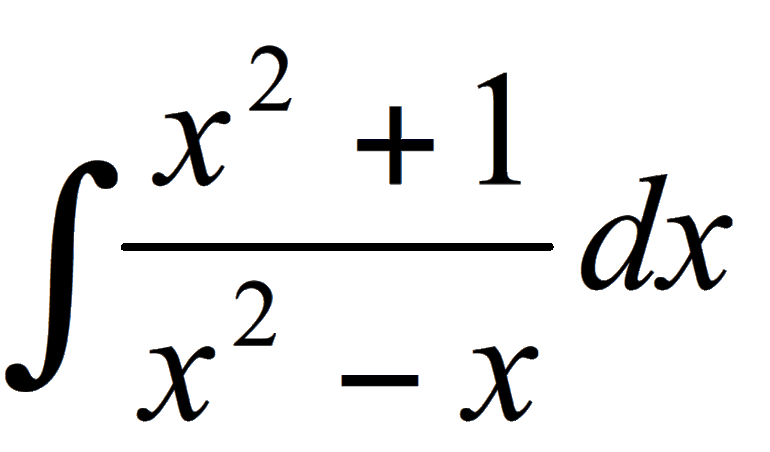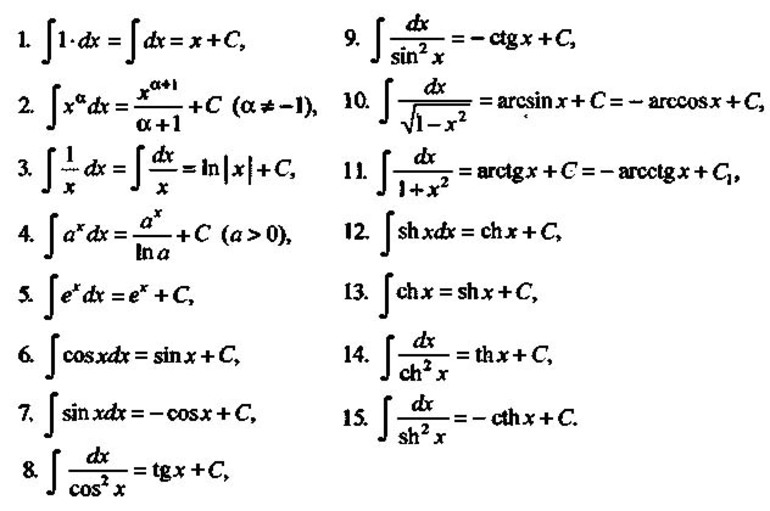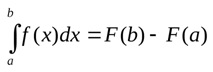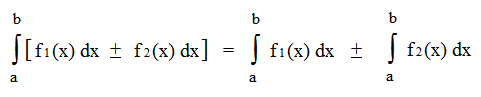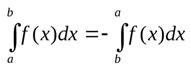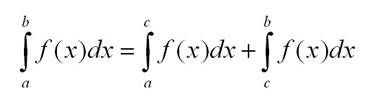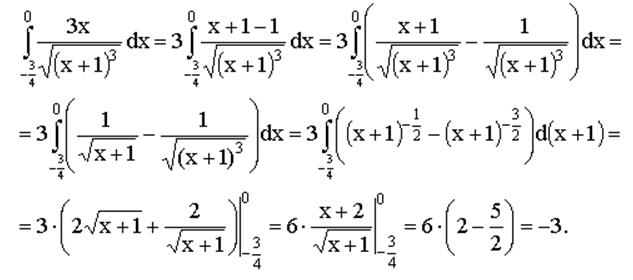На этой странице вы узнаете:
- Как связаны Ньютон и Лейбниц?
- Почему площадь криволинейной трапеции считается через интеграл?
Интеграл
В топ-5 страшилок по математике неизменно входит интеграл. Так ли он ужасен на самом деле?
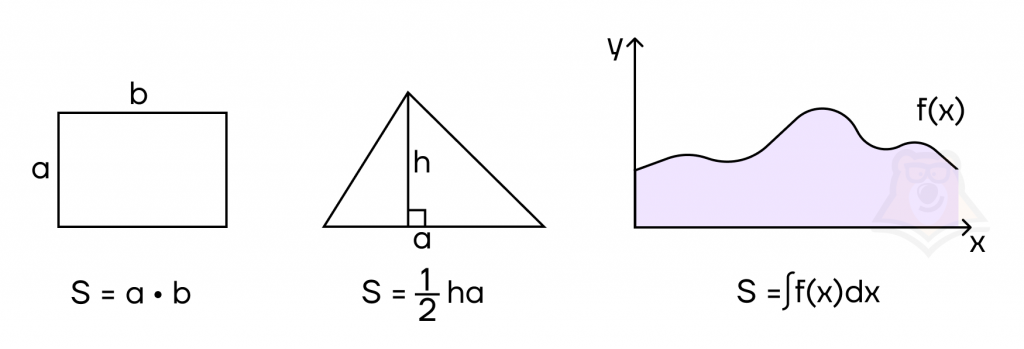
Если объяснять простыми словами, интеграл — это площадь фигуры под графиком функции. Например, в геометрии есть формулы, чтобы посчитать площадь прямоугольника или треугольника, а если нужно посчитать площадь фигуры с кривой стороной, заданной функцией, поможет интеграл.
Если у функции y = f(x) есть первообразная y = F(x), тогда множество значений первообразных у = F(x) + С называют неопределенным интегралом функции y = f(x)
Записывается это следующим образом:
(int f(x)dx = F(x) + C)
Какие бывают интегралы?
Интегралы бывают неопределенные и определенные.
Рассмотрим определенный интеграл. У такого интеграла в отличие от неопределенного есть предел интегрирования, то есть определённый отрезок.
Определенный интеграл функции на отрезке [a; b] – это приращение первообразных
Записывается это следующим образом:
(intlimits_a^b f(x)dx = F(b) — F(a))
Для данного интеграла пределом является отрезок от a до b
И Ньютон, и Лейбниц, бесспорно, являются великими учеными. Как и у обычных людей, у них бывают споры. Именно такой спор и послужил названию одной из формул в математике в честь этих двух замечательных ученых. Формула Ньютона-Лейбница используется для вычисления определенного интеграла. Она была выведена Ньютоном и Лейбницем независимо друг от друга. Есть мнение, что Ньютон свою версию создал раньше Лейбница, но опубликовал позже, из-за этого и случился спор, который завершился только после смерти обоих ученых.
Формула Ньютона-Лейбница
Если функция f(x) непрерывна на промежутке [a; b], то
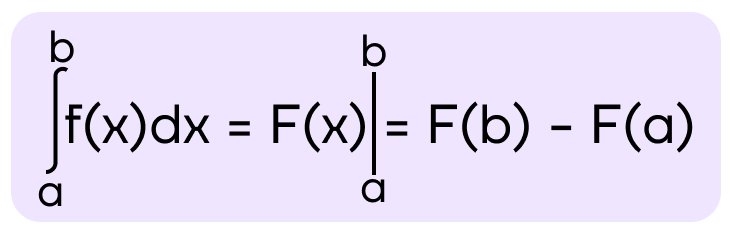
где F(x) – первообразная для функции f(x),
a – нижний предел интегрирования,
b – верхний предел интегрирования
Данная формула применяется для вычисления определенного интеграла
Пример вычисления определенного интеграла по формуле Ньютона – Лейбница:
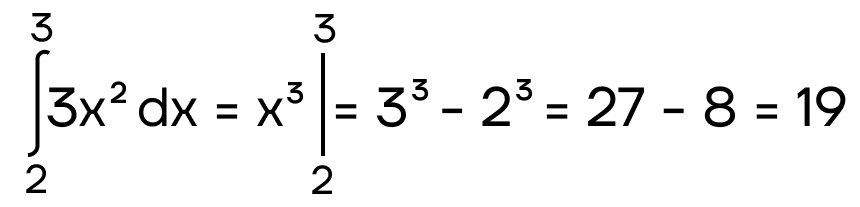
Интеграл для нахождения площади фигуры
Представим, что нам нужно посчитать расстояние, пройденное автомобилем с непостоянной скоростью в промежуток времени [a; b].
Нарисуем график.
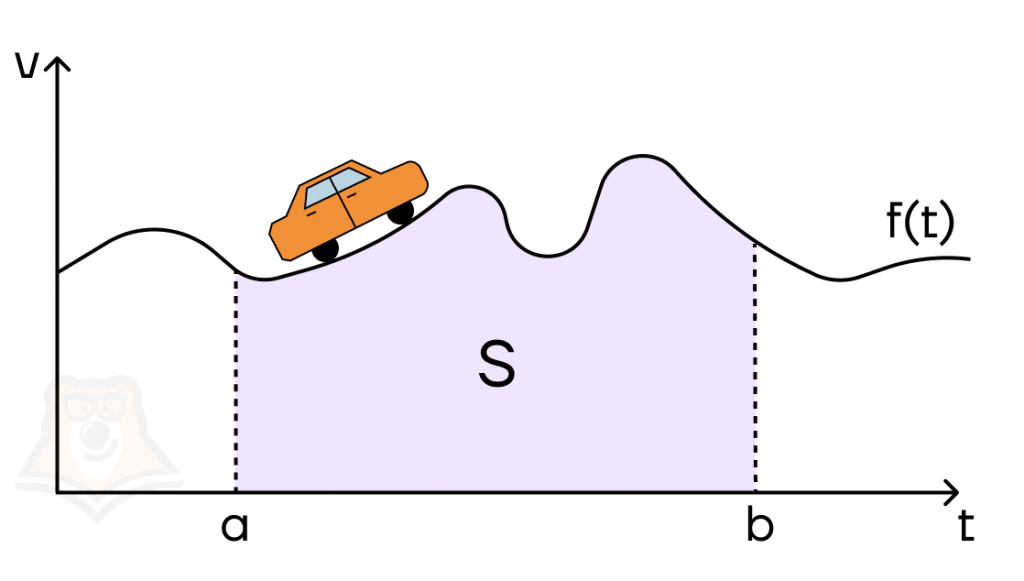
Скорость автомобиля V изменяется с течением времени, как f(t). Тогда, чтобы её найти, нам нужно посчитать площадь фигуры, ограниченной графиком функции f(t) на отрезке [a; b]. Такой фигурой будет являться криволинейная трапеция, а посчитать площадь можно с помощью интеграла. Далее мы подробно разберем, как это сделать.
Криволинейная трапеция – это фигура на плоскости, ограниченная графиком непрерывной функции на определенном отрезке, прямыми линиями и осью абсцисс.
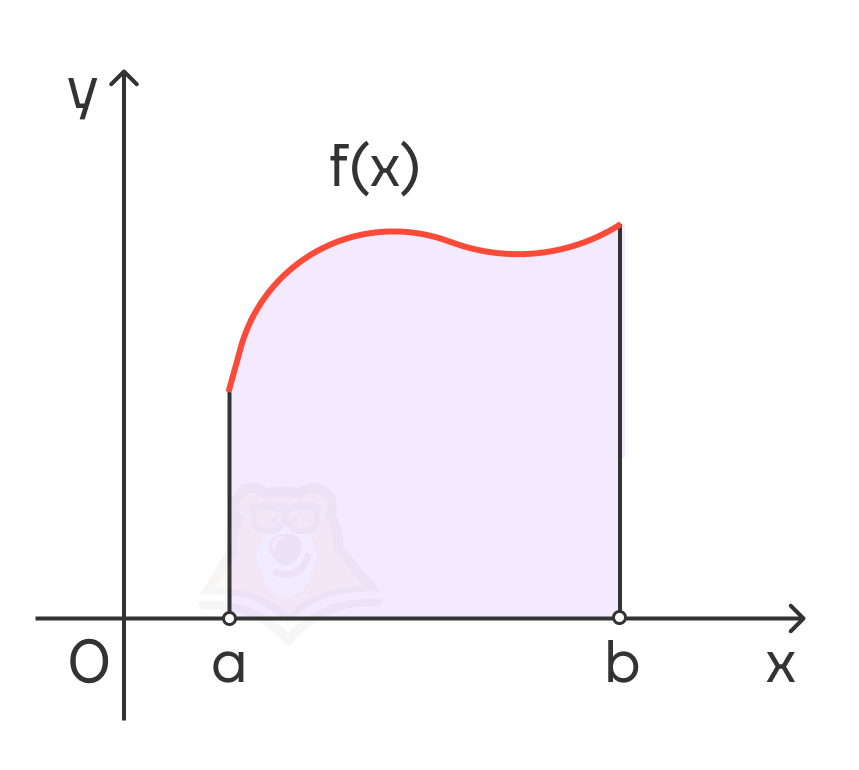
На данном рисунке фигура ограничена y = f(x), x = a, x = b, y = 0
Как найти площадь фигуры, используя интеграл?
Площадь такой фигуры, расположенной над осью абсцисс, можно посчитать, вычислив определённый интеграл по уже известной формуле Ньютона-Лейбница.
(S = intlimits_a^b f(x)dx)
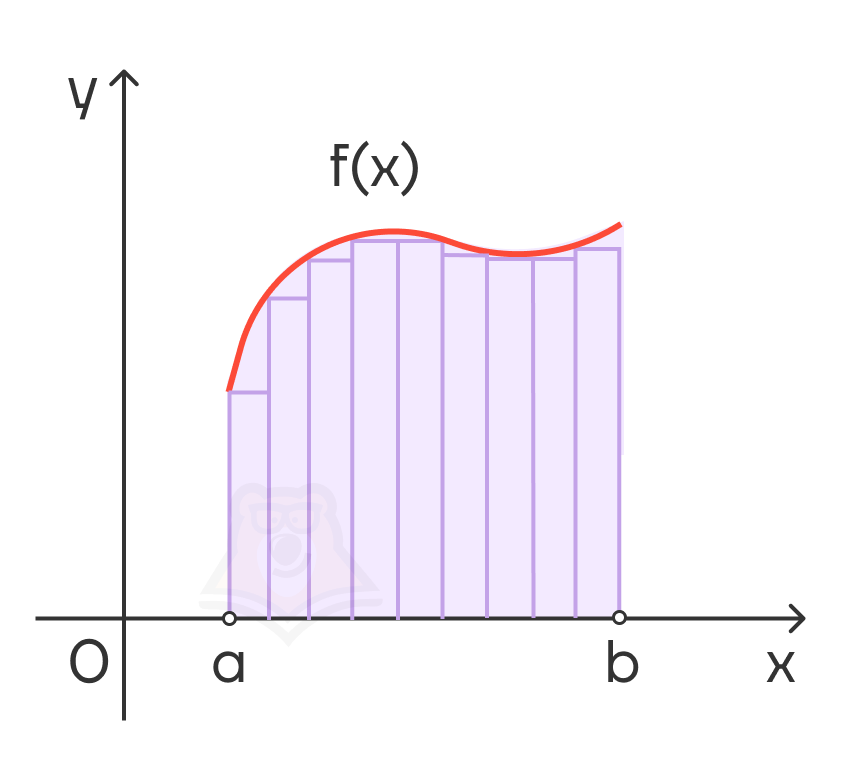
Чтобы понять это, разобьем фигуру на конечное число узких прямоугольных столбцов.
Найдем общую площадь, умножив высоту каждого столбика на его ширину и сложив все полученные значения, такая площадь будет приблизительной.
Если разделить данную фигуру на большее количество столбиков, только уже меньших по ширине, получим более точное значение. Повторять такое действие можно до бесконечности, следовательно, ширина будет стремиться к нулю, а количество прямоугольников — к бесконечности.
Сумму такого количества прямоугольников запишем в виде предела при количестве прямоугольников, стремящемся к бесконечности.
При таких условиях рассматриваемая сумма площадей сходится к пределу, описываемому следующим образом
, и равна какому-то числу.
А если фигура расположена под осью абсцисс, для вычисления площади фигуры нужно добавить минус к изначальной формуле.
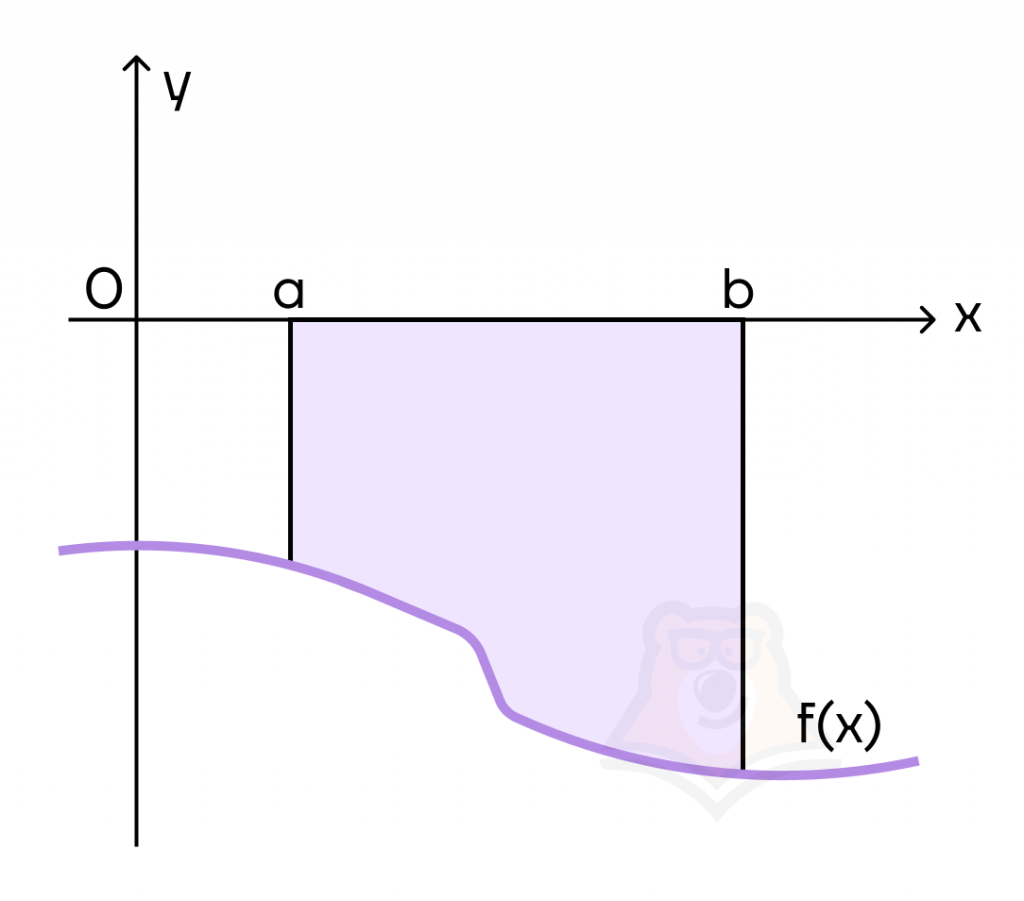
(S = -intlimits_a^b f(x)dx)
Если нужно найти площадь фигуры, ограниченной двумя функциями f(x) и g(x), то сначала данные функции приравниваются, так находится предел, а далее определяется функция, которая находится выше, и записывается формула
(S = intlimits_a^b (f(x) — g(x))dx)
где f(x) – функция находящаяся выше
g(x) – функция находящаяся ниже
a и b – границы предела
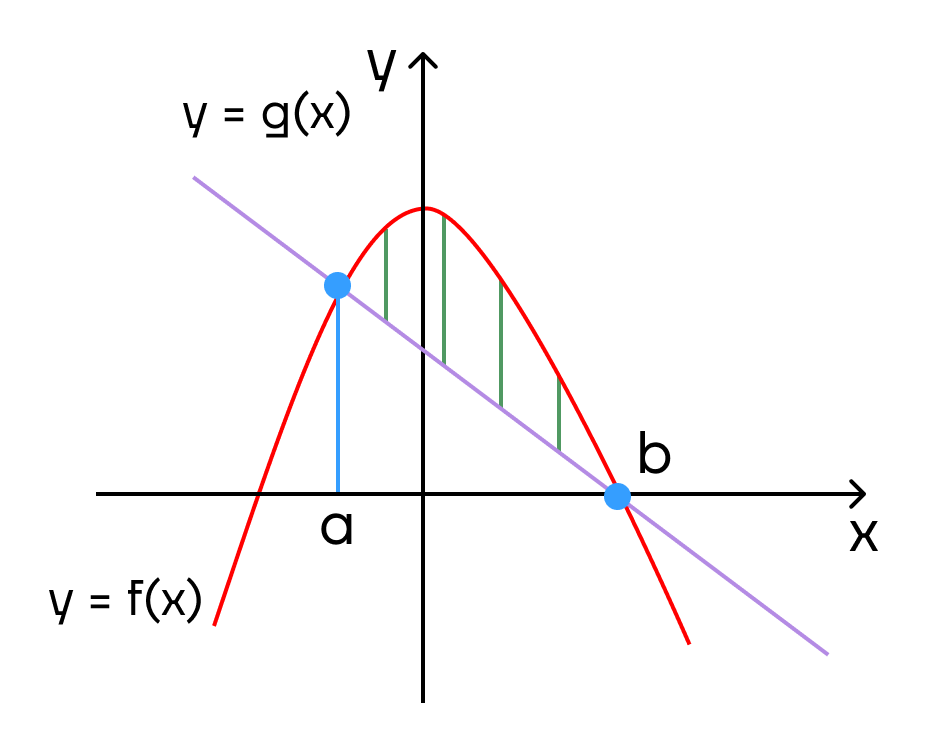
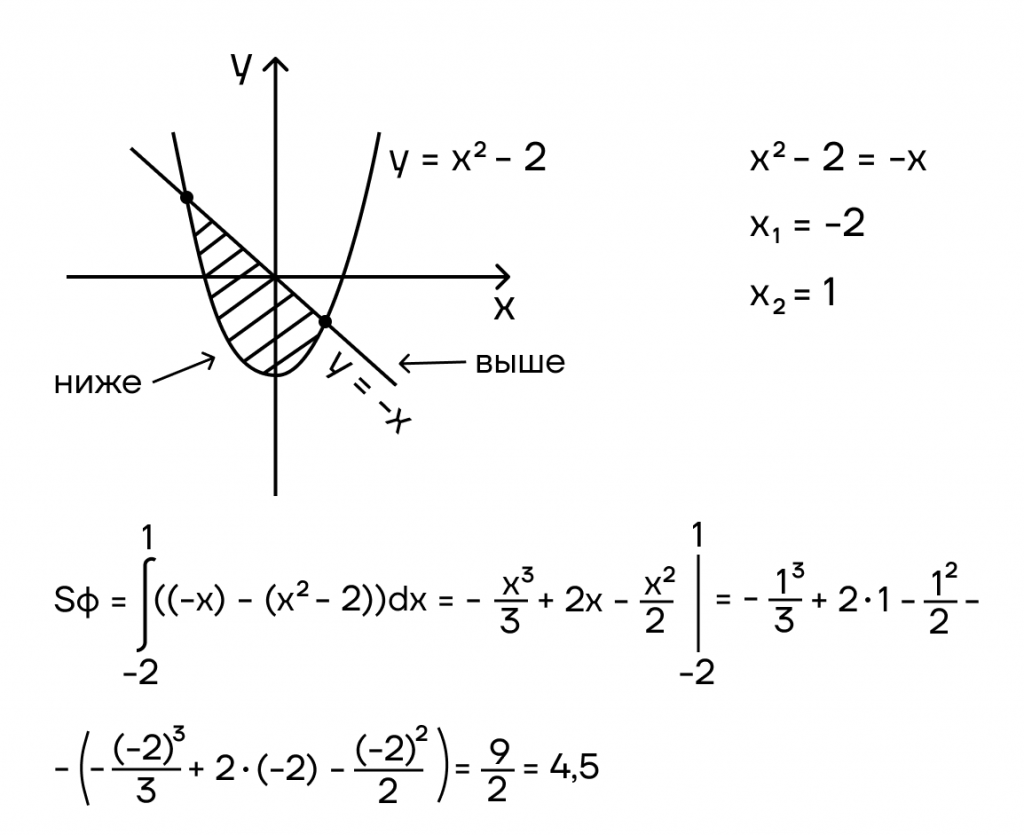
Пример:
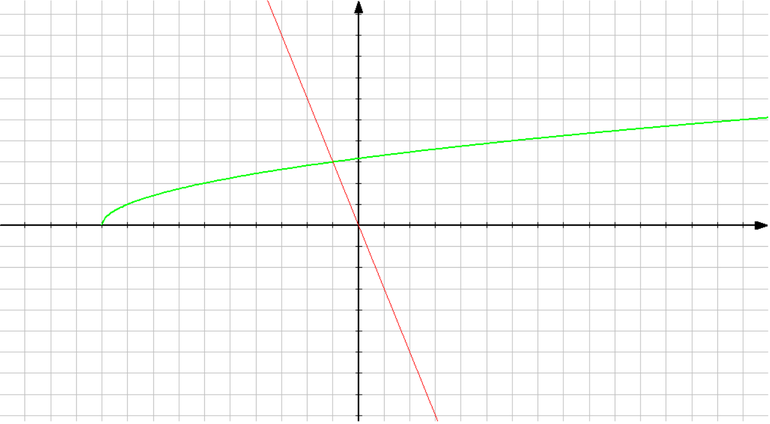
Найти площадь фигуры ограниченной функциями y=x2 — 2 и y = -x
Фактчек
- Интеграл — это площадь фигуры, находящейся под графиком функции.
- Неопределённый интеграл функции fx : (int f(x)dx = F(x) + C)
- Определенный интеграл функции fx на отрезке [a; b] : (intlimits_a^b f(x)dx = F(b) — F(a))
- Формула Ньютона-Лейбница (intlimits_a^b f(x)dx = F(x) |_a^b = F(b) — F(a))
- Формула для нахождения криволинейной трапеции над осью х
(S = intlimits_a^b f(x)dx) - Формула для нахождения криволинейной трапеции под осью х
(S = -intlimits_a^b f(x)dx) - Формула для нахождения площади фигуры, ограниченной двумя функциями
(S = intlimits_a^b (f(x) — g(x))dx), где
f(x) – функция находящаяся выше
g(x) – функция находящаяся ниже
Проверь себя
Задание 1.
Найдите значение интеграла (intlimits_1^5 3dx)
- 3
- 5
- 12
- 14
Задание 2.
Вычислите площадь фигуры ограниченной (y = sin x, x = 0, x = frac{pi}{2})
- 1
- 0
- 1,5
- 2
Задание 3.
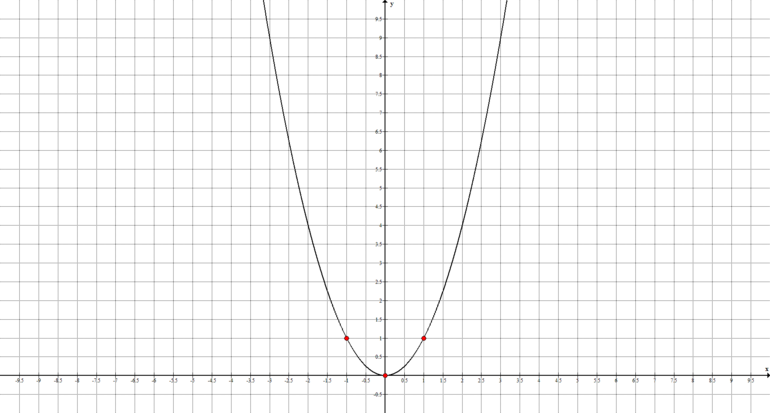
Вычислите площадь фигуры ограниченной y = 2x2 — 5, x = -1, x = 1
- 9
- (8frac{2}{3})
- (frac{20}{3})
- 8
Задание 4.
Вычислите площадь фигуры ограниченной y = x2 — 3 и y = -2x2 + 9
- 32
- 18
- 24
- 2
Ответы: 1. – 3; 2. – 1; 3. – 2; 4. – 1
Заканчивая главу о
первообразной, покажем, как понятие
первообразной (неопределенного интеграла)
теснейшим образом связано с определением
площади плоской фигуры. Причем
воспользуемся здесь интуитивным
представлением о площади плоской фигуры,
отложив точную постановку этого вопроса.
Пусть имеем непрерывную
на отрезке [a,b] функциюf(x),
принимающую лишь положительные
(неотрицательные) значения.
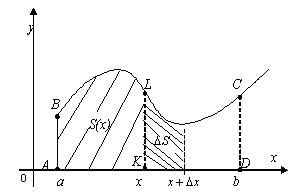
Рассмотрим фигуру
ABCD(рис. 24), ограниченную кривойy
=f(x), прямымиx = a,x =bи отрезком оси0X; такую фигуру
называют криволинейной трапецией.
Изучим вопрос о площади криволинейной
трапеции. Для этого возьмем некоторую
переменную точкуx, лежащую на
интервале [a,b], и рассмотрим
площадь фигурыABLK. При измененииxэта последняя площадь будет, очевидно,
соответственно изменяться, причем
каждому значению переменнойxотвечает вполне определенное значение
площади криволинейной трапеции. Поэтому
площадь криволинейной трапецииABLKявляется некоторой функцией отx;
обозначим эту функциюS(x). Найдем
(если это возможно) производную функцииS(x) при измененииx. Для этого
дадимxприращение (например,
положительное);
тогда площадьS(x) получит
приращение.
ОбозначимmиMсоответственно
наименьшее и наибольшее значенияf(x)
на промежуткеи сравним площадь
с площадями прямоугольников
и
.
Очевидно,или
.
Рис.
24
Если теперь
,
то,
вследствие непрерывностиf(x)
значения,
;
существует предел.
Таким образом, мы получили замечательный
результат.
Теорема.Производная от переменной площади по
переменной абсциссеxравна значению
функции в этой переменной точкеf(x).
Иными словами,
переменная площадь S(x) представляет
собой одну из первообразных – для данной
функцииy =f(x):.
Так как все
первообразные отличаются друг от друга
на постоянную величину c, то еслиF(x) какая-либо первообразная дляf(x), тогдаS(x) =F(x)
+c.
Положив здесь x=aи считая (очевидно)S(a)=0,
получим 0 =F(a) +c,c= –F(a).
Окончательно,
S(x)=F(x)–F(a), гдеx– любая точка из интервала [a,b].
В частности, для получения площади всей
криволинейной трапецииABCDследует
взятьx=b:
.
Этот важный результат
называют теоремой Ньютона-Лейбница. Мы
еще встретимся с этой теоремой в
дальнейшем: площадь криволинейной
трапеции Sравна разности значений
(произвольной) первообразнойF(x)
в концах интервала [a,b].
3.4. Определенный интеграл
Вернемся вновь к
задаче определения площади криволинейной
трапеции, ограниченной непрерывной
кривой y=f(x),,
прямымиx=a,x=bи отрезком
осиOX.
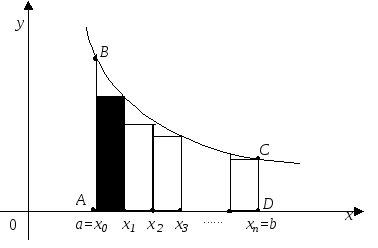
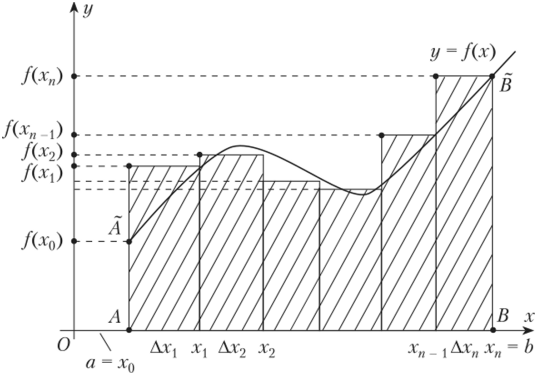
Разобьем отрезок
[a,b] точкаминаnравных частей (рис. 25). Получимn“малых” отрезков
;
длина каждого отрезкаобозначается
,
k=1, 2, …,n; в нашем случае длины всех
отрезков одинаковы:.
Рис.
25
Проведя через точки
деления прямые, параллельные оси 0Y,
мы разобьем криволинейную трапециюABCDнаnмалых криволинейных
трапеций – полосок с площадью(k=1, 2,…,n). Очевидно, площадь всей
криволинейной трапецииABCD
.
Эту последнюю сумму
записывают так:
,
где греческая буква ∑ – это знак суммы,
а символозначает, что суммируютсяnслагаемых
при изменении индексаkот 1 доn.
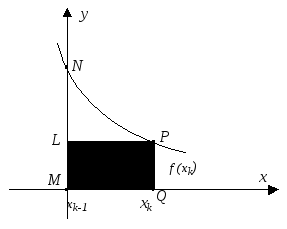
Заменим теперь
площадь
малой криволинейной фигурыMLPQ(рис.
26) площадью прямоугольникаMLPQ, равной.
Искомая площадьSкриволинейной
трапеции приближенно равна площади
ступенчатой фигуры:
.
Рис.
26
Очевидно, чем меньше
длина промежутков
,тем
точнее ступенчатая фигура приближает
нашу криволинейную трапецию.
Будем теперь
увеличивать вдвое число n точек деления,
уменьшая вдвое длину интервалов
разбиения.
Получим последовательность
сумм
, (*)
где
– площадь ступенчатой фигуры изnпрямоугольников. Естественно за точное
значение площадиSкриволинейной
трапеции принять предел последовательностиплощадей ступенчатых фигур, когда
(при этом все длины
стремятся к нулю,
).
Сумма вида (*)называется интегральной суммой, а
предел, к которому стремится
последовательность интегральных суммпри
,
если такой предел существует, называется
определенным интегралом функцииf(x)
на отрезке [a,b] и обозначается
символом(читается – интеграл отaдоbфункцииf(x)).
Итак,
.
Замечание.Мы
рассмотрели здесь только частный случай
последовательности интегральных сумм:
разбиение отрезка [a,b] сделано
так, что все(k=1, 2,…,n) равны между собой,
, точки
являются правыми концами промежутка
,
а функцияf(x) – непрерывна и
неотрицательна. Вообще говоря,
рассматриваются интегральные суммы
более общего вида, а именно:
1) точки деления
выбираются произвольно, не обязательно
на равном расстоянии друг от друга;
2) на каждом отрезке
длины
выбирается произвольная точка
;
3)
сумму
называют интегральной суммой (Римана)
для функцииf(x)
на отрезке [a,
b];
4) определенным
интеграломназывается такое числоI, которое удовлетворяет условию:
для любого (сколь угодно малого)
положительного числанайдется такое положительное числоδ,
что прии любом выборе точек
выполняется неравенство
.
Фактически определенный
интеграл Iявляется пределом
интегральных сумм при стремлении к нулю
всех отрезков разбиения, если этот
предел существует и не зависит от выбора
точек деленияи выбора точек
.
Функции f(x),
для которых определенный интегралсуществует, называются интегрируемыми
(по Риману) на отрезке [a,b]. К
таким функциям относятся любые непрерывные
на [a,b] функции, а также
кусочно-непрерывные, т.е. имеющие на
отрезке интегрирования лишь конечное
число точек разрыва первого рода.
Очевидно, что интегрируемые на отрезке
функции ограничены на этом отрезке.
Возвращаясь к задаче
о площади, с которой мы начали, видим,
что площадь криволинейной трапеции,
ограниченной непрерывной кривой y=f(x), гдена [a,b], численно равна определенному
интегралу.
Этот факт выражает
геометрический смысл определенного
интеграла.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
Общие сведения
Вычислить площадь фигуры на плоскости считается довольно простой операцией. Для ее выполнения необходимо знать только формулу. Существенно усложняет задачу фигура, ограниченная прямыми.
Одной из них считается криволинейная трапеция. Ее площадь можно определить только при нахождении значений определенного интеграла.
Операция интегрирования считается довольно сложной, поскольку необходимо знать основные правила. Перед нахождением площади криволинейной трапеции специалисты рекомендуют внимательно изучить и освоить правила интегрирования основных функций.
Разбирается неопределенный интеграл, а затем осуществляется переход к более сложным операциям.
Информация об интегралах
С понятием интеграла связано много направлений научных отраслей. Обозначается он символом «∫». С помощью интеграла открываются большие возможности по быстрому и эффективному нахождению значений следующих величин: площади криволинейной трапеции, объема тела вращения, поверхности, пути при неравномерном движении, массы неоднородного физического тела и так далее.
Упрощенный вариант представления и определения интеграла — сумма бесконечно малых слагаемых. Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:
- Неопределенный.
- Определенный.
Операция нахождения первого типа значительно проще второго. Это объясняется тем, что во втором случае следует не только найти первообразную, но и выполнить правильную подстановку значений.
Неопределенным интегралом функции вида f(х) называется такая первообразная функция F(х), производная которой равна подинтегральному выражению. Записывается это таким образом: ∫(f(x)) = F(х) + С.
Последняя величина является константой, поскольку при выполнении операции нахождения производной константа равна 0.
Для нахождения первообразной используется специальная таблица интегралов:
Рисунок 1. Таблица интегралов и их первообразные.
В таблице приведены простые функции. Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).
Криволинейные фигуры
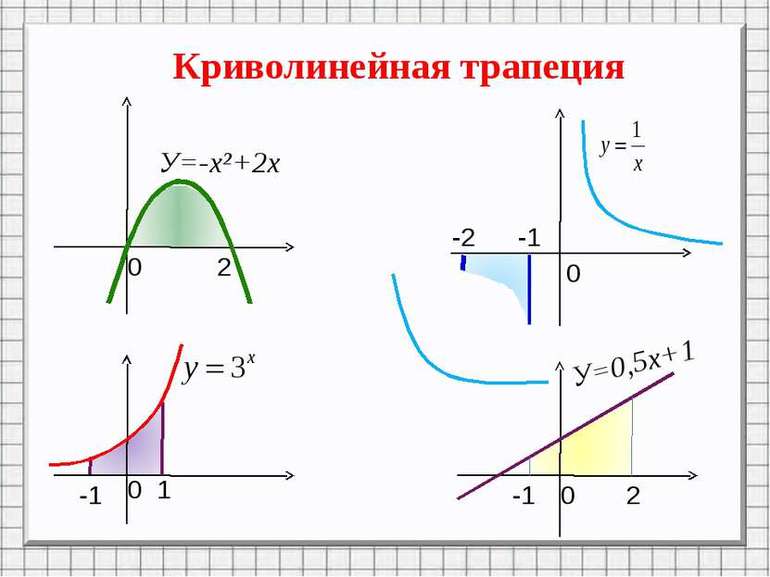
Криволинейная фигура (трапеция) — класс плоских фигур, которые ограничены графиком неотрицательной и непрерывной функции, а также осью ОУ и прямыми (х = а, х = b). Она изображена на рисунке 2. Для нахождения ее площади следует использовать определенный интеграл.
Рисунок 2. Фигуры с криволинейными сторонами.
Интегрирование разбивает фигуру на прямоугольные части. Длина каждой из них равна ординате y = f(х) через промежутки, которые очень малы, по оси декартовой системы координат (есть еще и полярная) ОХ на отрезке [a;b]. Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.
Криволинейная трапеция — геометрическая фигура с неровными сторонами, которые образовались в результате пересечения графика непрерывной функции с осями абсцисс и ординат.
Применение обыкновенных методов нахождения площади этой фигуры невозможно, поскольку она обладает одной или несколькими неровными сторонами (кривыми линиями).
Способы вычисления и рекомендации
Для расчетов площади криволинейной трапеции используется несколько методов. Их условно можно разделить на следующие: автоматизированные и ручные. Первый из них выполняется при помощи специализированного программного обеспечения (ПО). Примером является онлайн-калькулятор, который не только находит площадь заданной фигуры, но и изображает ее в декартовой системе координат.
Существует и другое ПО, которое является более «мощным». К нему можно отнести наиболее популярные среды: Maple и Matlab. Однако существует множество программ, написанных на языке программирования Python. Программы нужны также при освоении темы интегрирования. Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.
Новичку для автоматизированных вычислений рекомендуется применять различные онлайн-калькуляторы. Однако следует выделить неплохую программу, которая обладает довольно неплохими функциональными возможностями.
Она называется Integral calculator и представляет собой очень удобное приложение для Android-устройств. Кроме того, можно скачать подобное ПО для Linux, Mac и Windows.
Программа — это калькулятор, который используется для нахождения интегралов и производных, а также его можно применять для решения уравнений интегрального и дифференциального типов. Integral calculator обладает такими функциональными возможностями:
- Вычисление производных.
- Нахождения первообразных для определенных и неопределенных интегралов.
- Решение систем уравнений.
- Выполнения операций над матрицами и определителями.
- Построение графиков заданных функций в 2D и 3D.
- Расчет точек перегиба.
- Вычисление рядов Фурье.
- Решение дифференциальных уравнений линейного типа первого и второго порядков.
Однако специалисты не рекомендуют использовать приложения такого типа, поскольку нужно уметь решать подобные задачи самостоятельно. Любые математические операции развивают мышление, а злоупотребление ПО приводит к значительной деградации. Решать какие-либо задачи рекомендуется также людям, которые не имеют отношения к математической сфере.
Основной алгоритм
При нахождении площади криволинейной трапеции рекомендуется следовать определенному алгоритму. Он поможет избежать ошибок, поскольку задача разбивается на несколько простых подзадач, решение которых довольно просто контролировать. Алгоритм имеет следующий вид:
- Нужно прочитать и понять условие задачи.
- Начертить декартовую систему координат.
- Построить график заданной функции.
- Изобразить линии, ограничивающие фигуру.
- После определения границ нужно аккуратно заштриховать фигуру.
- Вычислить неопределенный интеграл функции, которая дана в условии.
- Посчитать площадь, подставив значения ограничивающих прямых в первообразную.
- Проверить решение задачи при помощи программы.
Первый пункт — внимательное чтение условия задачи. Этап считается очень важным, поскольку формирует дальнейший алгоритм. Необходимо выписать все известные данные, а затем подумать над дальнейшим решением задачи. Следует обратить особое внимание на график функции, который при возможности нужно упростить. Далее следует выписать линии, которые будут ограничивать фигуру.
Следующий пункт считается наиболее простым, поскольку нужно начертить обыкновенную систему координат. В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.
Третий пункт алгоритма — правильное построение графика функции. В этом случае нет необходимости составлять таблицу зависимости значения функции от аргумента. График должен быть схематичным. Например, если это парабола, то нужно ее изобразить. В этом случае необходимо ознакомиться с основными базовыми функциями и их графиками.
Следующим шагом является правильное изображение прямых. Если ее уравнение имеет следующий вид «x = 5» или что-то подобное, то она будет проходить параллельно оси ОУ. Например, при y = 10 прямая проходит параллельно оси ОХ. В других случаях нужно составить таблицу зависимостей значений уравнения прямой от переменной. Следует брать всего два значения аргумента, поскольку их достаточно для проведения прямой.
После всех операций образуется фигура, которая ограничена линиями. Ее необходимо заштриховать. После этого вычисляется неопределенный интеграл заданной функции. Необходимо воспользоваться табличными значениями первообразных на рисунке 2. Однако здесь есть небольшой нюанс: константу записывать нет необходимости. Она «уничтожается» при подстановке в формулу Ньютона-Лейбница.
В полученное значение следует подставить значения границ. Кроме того, необходимо обратить особое внимание на знак формулы. При отрицательном значении границы формула принимает следующий вид: F(x)|(-a;b) = F(b) — F(-a) = F(b) + F(a). Проверка правильности решения выполняется с помощью ПО.
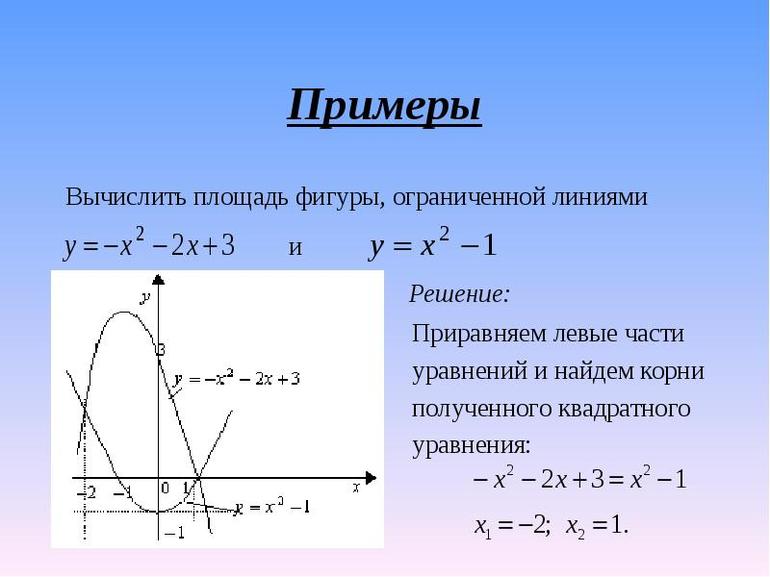
Примеры решения
Для закрепления теоретического материала специалисты рекомендуют решить несколько задач. В качестве примера можно взять криволинейные трапеции, изображенные на рисунке 2.
Разновидность параболы
В первом примере функция вида y = -x^2 + 2x и ось ОХ образуют фигуру. Необходимо найти ее площадь. Из функции видно, что ветви параболы направлены вниз (отрицательный знак перед квадратом). Точки пересечения находятся следующим образом:
- Тело функции приравнивается к 0: -х^2 + 2x = 0.
- Выносится общий множитель: -x(x-2) = 0.
- Решаются обе части уравнения.
- Первый корень: -х1 = 0 или х1 = 0.
- Для нахождения второго нужно решить другую часть уравнения: х2-2 = 0. Отсюда, х2 = 2.
Ветви параболы проходят через координаты по ОХ: 0 и 2 соответственно. Координата «х» вершины точки параболы находится с помощью подстановки в формулу: x = -b/(2*a) = -2 / -2 = 1. В этом случае координата «у» вычисляется следующим образом: y = -(1^2) + 2 * 1 = -1 + 2 = 1. Точка с координатами (1;1) является вершиной параболы. Границы интегрирования — координаты по ОХ, через которые проходят ветви параболы.
После всех операций следует вычислить неопределенный интеграл функции, воспользовавшись таблицей на рисунке 1: ∫ (-х^2 + 2x) dx = — (x^3 / 3 + x^2) + C = x^2 — x^3 / 3 + C. После этого следует подставить начальное и конечное значения (константа убирается): S = x^2 — x^3 / 3 = (2^2 — 2^3 / 3) — (0^2 — 0^3 / 3) = 4 — 8/3 = 4 / 3 (кв. ед.). Последняя запись является единицей измерения площади. Она обозначается в условных единицах, так как в условии задачи размерность сторон фигуры не указана.
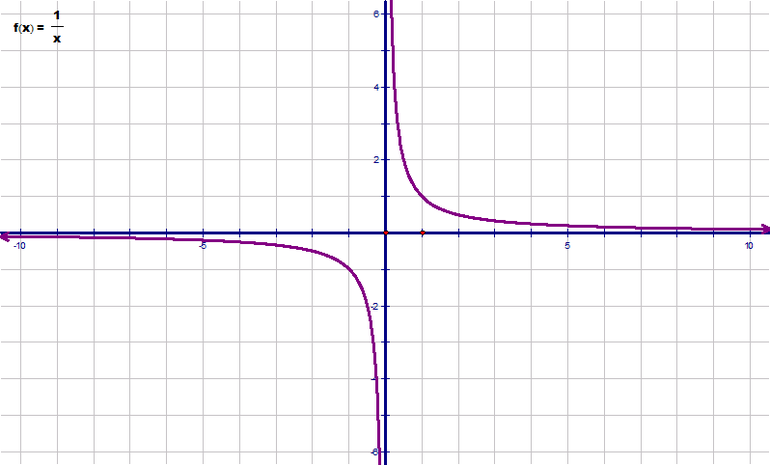
Гипербола, степенная и прямая
На следующем рисунке изображен график функции гиперболы (у = 1 / х). Прямые, которые ограничивают график, описываются следующими законами: у1 = -2 и у2 = -1. Для вычисления площади заданной фигуры следует взять интеграл: ∫(1/х) dx = ln (|x|) + С. Для окончательного решения необходимо подставить значения в натуральный логарифм: S = ln (2) — ln (1) = 0,6931 — 0 = 0,6931 (кв. ед.).
Фигура, которая ограничена прямыми y1 = -1 и y2 = 1, и представлена функцией вида y = 3^x. Площадь находится следующим образом: S = ∫ (3^x) dx = 3^x / (ln(|3|)) = [3^1 / (ln(3))] — [3^(-1) / (ln(3))] = (3 / 1,0986) — ((1/3) / 1,0986) = 2,7307 — 0,3034 = 2,4273 (кв. ед.).
Последняя фигура представлена графиком прямой y = 0,5х + 1, которую ограничивают прямые х1 = -1 и х2 = 2. Значение площади можно найти таким способом: S = ∫ (0,5х + 1) dx = (0,5 * х^2) / 2 + x = [((0,5 * 2^2) / 2) + 2] — [((0,5 * (-1)^2) / 2) + (-1)] = 3 — 0,75 = 2,25 (кв. ед.).
Для определения значения площади криволинейной фигуры (трапеции) необходимо использовать определенные интегралы. При решении нужно внимательно следить за знаками и первообразными из таблицы на рисунке 1.
За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов
Почему вы не знаете, как решать интегралы
А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.
Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:
- вычисление площади фигуры.
- вычисление массы тела с неравномерной плотностью.
- определение пройденного пути при движении с непостоянной скоростью.
- и др.
Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.
Главная причина незнания – отсутствие понимания практической значимости интегралов.
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Интеграл – что это?
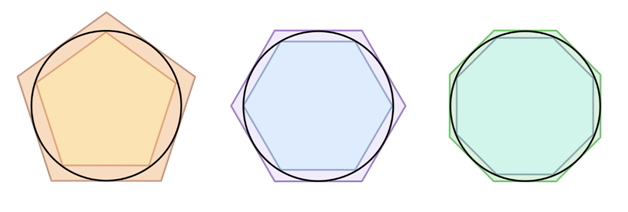
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.
Метод исчерпывания для определения площади круга
В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Объясняем понятие «Интеграл»
Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.
Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.
Интеграл записывается так:
Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).
Неопределённый интеграл
Неопределенный интеграл не имеет границ интегрирования.
Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».
Пример решения неопределенного интеграла.
Определённый интеграл
В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.
Точки A и B на оси X – есть ограничение зоны определения интеграла
Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:
Пример решения определенного интеграла
Таблица интегралов для студентов (основные формулы)
Скачайте формулы интегралов, они вам еще пригодятся
Как вычислять интеграл правильно
Существует несколько простейших операций для преобразования интегралов. Вот основные из них:
Вынесение константы из-под знака интеграла
Разложение интеграла суммы на сумму интегралов
Если поменять местами a и b, знак изменится
Можно разбить интеграл на промежутки следующим образом
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.
Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.
Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Приращение – количественное изменение функции при некотором изменении аргумента.
Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.
Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.
Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.
Заключение
Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие «интеграл»
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
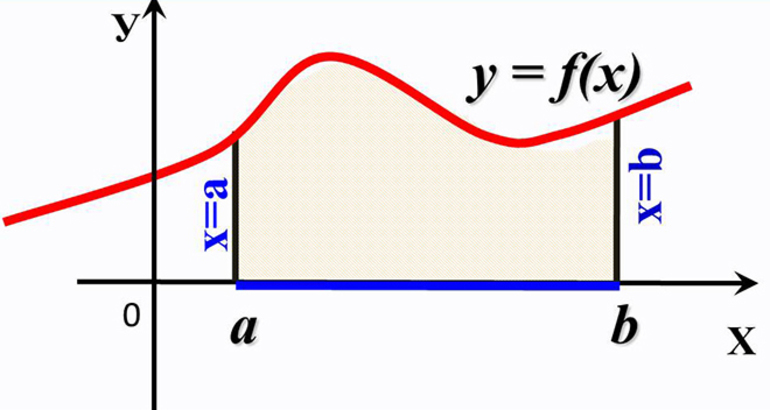
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
«Интеграл»
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
- Константу можно выносить из-под знака интеграла:
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Линейность:
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых точках a, b и с:
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.