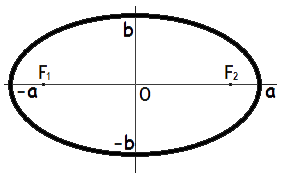Как найти площадь математических фигур - Avtoru.top

Формулы площади геометрических фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p — a)(p — b)(p — c)
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,

p = a + b + c — полупериметр треугольника.

2

Формулы площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

S = a²
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d₁, d₂ — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.

Формулы площади ромба

Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

S = a² · sin α
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d₁, d₂ — длины диагоналей.

Формулы площади трапеции

Формула Герона для трапеции

S = a + b √(p-a)(p-b)(p-a-c)(p-a-d)

|a — b|
Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,

p = a + b + c + d — полупериметр трапеции.

2

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними

Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника,
d₁, d₂ — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)

Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

S = p · r
Формула площади четырехугольника по длине сторон и значению противоположных углов

S = √(p — a)(p — b)(p — c)(p — d) — abcd cos²θ

где S — площадь четырехугольника,

a, b, c, d — длины сторон четырехугольника,

p = a + b + c + d2 — полупериметр четырехугольника,

θ = α + β2 — полусумма двух противоположных углов четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность

S = √(p — a)(p — b)(p — c)(p — d)

Формулы площади круга

Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.

S = π r²
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.

Формулы площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = π · a · b

где S — Площадь эллипса,

a — длина большей полуоси эллипса,

b — длина меньшей полуоси эллипса.

Источник

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Запомните!

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S = a · a

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Запомните!

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S = a · b

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Запомните!

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Запомните!

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Запомните!

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см²

S_ABC =
S_ACD = 10 см²

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

3 декабря 2015 в 22:54

Ирина Петренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ирина Петренко
Профиль
Благодарили: 0

Сообщений: 1

как написать правильно площадь треугольника?

0
Спасибо thanks
Ответить

9 декабря 2015 в 19:41
Ответ для Ирина Петренко

Тима Клюев
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Тима Клюев
Профиль
Благодарили: 0

Сообщений: 8

S(рисуешь мини треугольник) = ,,,,,

0
Спасибо thanks
Ответить

Источник

Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.

Некоторые свойства площади фигур

Если многоугольники равны, то они имеют равные площади.
Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Рис. (1). Нахождение площади многоугольника

Рассмотрим, как найти площадь у разных фигур.

Площадь квадрата

Площадь квадрата равна квадрату его стороны.

S=a2

, где

— длина стороны квадрата.

Площадь прямоугольника

Площадь прямоугольника равна произведению его длины на ширину (смежные стороны).

S=a⋅b

, где

— длина и ширина.

Площадь параллелограмма равна произведению основания на высоту.

Рис. (2). Параллелограмм

S=a⋅h

(

) — основание,

(

) — высота.

Площадь ромба равна половине произведения его диагоналей.

Рис. (3). Ромб

Рис. (4). Треугольник

Площадь треугольника равна половине произведения основания на высоту.

S=a⋅h2

, где

(

) — основание,

(

) — высота треугольника.

Площадь прямоугольного треугольника равна половине произведения его катетов.

Рис. (5). Трапеция

Площадь трапеции равна половине суммы оснований, умноженной на высоту.

S=a+b2⋅h

, где

(

) и

(

) — основания,

(

) — высота.

Площадь круга и кругового сектора

Рис. (6). Круг

S=π⋅R2360°⋅α

— площадь кругового сектора.

Более подробно ознакомиться с примерами можно здесь.

Источник

Площадь — это величина пространства, которое ограниченное замкнутым контуром (периметром фигуры).

Площадь прямоугольника находится по формуле: длину умножить на ширину фигуры (S = a*b)

Плошадь квадрата можно найти по двум формулам:

через известное значение одной из сторон: одну из сторон квадрата поднести к квадрату или умножить саму на себя (S = a*a)
через диагональ квадрата: диагональ квадрата поднести к квадрату и умножить на одну/вторую (или получившееся значение разделить на два) (S = 1/2* c*c) (S = c*c : 2)

Площадь треугольника можно найти через основание и высоту фигуры: основание треугольника умножить на высоту и разделить на два (умножить на одну/вторую) (S = a*h :2) (S = a*h *1/2)

Площадь круга можно найти, зная радиус или диаметр фигуры:

число «пи» умножить на радиус круга, поднесенный к квадрату (S = π * r*r)
число «пи», разделенное на четыре, умножить на диаметр, поднесенный к квадрату: (S = π/4 * D*D)

система выбрала этот ответ лучшим

Hamster1337
[28.6K]

2 года назад

Площадь — это величина поверхности какой либо фигуры (квадрата, треугольника и т.д). Например, квадрат 2 на 2 (см) имеет площадь 4 см (по формуле a^2). Более подробно узнать о формулах вычисления площадей простейших фигур, вписанных и описанных в круг фигур и т. д. можно здесь.

Михаил 33
[36.4K]

5 лет назад

Нам постоянно приходится слышать о площади геометрических фигур, и можно полноценно сказать, что это одна из наиважнейших составляющих всей геометрии, как научной дисциплины.

Немаловажным фактором является то, что необходимость определить величину площади чего-либо возникает в нашей жизни очень часто.

Для примера возьмём обычный ремонт квартиры или дома.

Сколько раз приходится вычислить площадь комнаты, потолка, стен, пола и т.д.

И любые ошибки при данных вычислениях приводят лишь к одному, к нашим избыточным денежным затратам, так как закупка стройматериалов полностью зависит от площади, для которой предназначаются те или иные стройматериалы.

Примеров того, что понятие площади необходимо знать всем, сотни, но речь не об этом.

И так, что такое площадь?

Площадью называется часть плоскости, заключённой внутри какой либо геометрической фигуры. Соответственно и нахождение её будет зависеть именно от того, в какой именно фигуре заключена данная часть плоскости.

Как находится площадь отдельных геометрических фигур:

AlexSEO
[85.9K]

3 года назад

Площадь (ранее принятое название — квадратура), и это следует сразу же отметить, относится к фигуре (геометрической) плоской (возможно — искривленной), где есть два измерения (при вводе третьего измерения получается объем), например — длина/ширина. По сути — это не что иное, как размер той или иной фигуры или совокупность (сложение) всех точек, входящих в нее.

Если фигуры стандартные (круг/квадрат/прямоугольник/трапеция/треугольник), то найти их площадь просто — есть соответствующие формулы, нужно лишь знать размеры, например, зная сторону такой фигуры, как квадрат, легко найти площадь, просто умножив ее (или возведя в квадрат) на саму себя. Другие формулы:

Если фигура сложная, то тут применяют интегралы (для теоретических вычислений) или же специальные приспособления, например, планиметр или палетку (для практических измерений).

Alex2837
[113K]

более года назад

Понятие площади фигуры изучается на уроках математики в средних классах. Очень часто ученики путают эту меру с периметром геометрической фигуры.

Если не обращаться к научной литературе, то понятие площади простыми словами можно обозначить, как часть плоскости, которая ограничивается сторонами фигуры.

Например, площадь треугольника ограничивается его тремя сторонами, площадь прямоугольника или квадрата ограничивается четырьмя сторонами.

Для вычисления площади используются специальные формулы. Для каждой геометрической фигуры имеется своя отдельная формула. Например, для определения площади прямоугольника, достаточно просто умножить его длину на ширину.

Мудрый Датч
[75.5K]

2 года назад

Площадь является мерой того, сколько на плоской поверхности имеется пространства.

В математике вычисляются разными путями площади фигур. Если мы возьмём, к примеру, прямоугольник, то его площадь следует определять как произведение его высоты и ширины, а площадь квадрата, где сторона обозначается буквой «а», будет равняться

=а*а («а» в квадрате). Но и будет несправедиво не упомянуть площадь такой фигуры как треугольник, а равна площадь треугольника произведению половины его основания на высоту. Ниже привожу небольшую подсказку в определении площади фигур.

Domino-12
[201]

более месяца назад

В математике площадью называют величину, характеризующую протяженность двумерной геометрической фигуры (прямоугольника, треугольника и т.д.) или области на плоскости.

Площадь обозначается буквой S.

Для каждой геометрической фигуры существуют формулы площади, выбор формулы зависит от того, что дано в условии задачи.

Вот, например, несколько формул для нахождения площади треугольника:

Если известны все 3 стороны, то можно воспользоваться 2 формулой (она называется формулой Герона) — в ней a, b, c являются сторонами, а p — полупериметром (нужно сложить числовые значения всех сторон и разделить на 2).

А если мы знаем, чему равна высота и основание треугольника, то площадь можно посчитать по 1 формуле — половина произведения основания на высоту.

Отдельный случай — это нахождение площади произвольного многоугольника.

Здесь тоже имеются формулы, но в некоторых случаях можно сделать и так: разбить многоугольник на несколько стандартных фигур и найти их площадь, площадь многоугольника будет равна сумме площадей этих фигур.

То есть:

S = S1 + S2 + S3 = …

А в некоторых случаях проще достроить многоугольник до прямоугольника или квадрата, найти площадь полученной фигуры, а затем вычесть из неё площади лишних областей.

ЕкатеринаКрест
[34]

5 лет назад

Площадь-часть плоскости, заключённая внутри замкнутой геометрической фигуры. Как всем известно,фигуры есть самые разнообразные,но самое элементарное-нахождение площади(S) прямоугольника,треугольника. Чтобы найти S прямоугольника,нужно умножить ее ширину на длину,то есть а*в. Квадрат-тот же самый прямоугольник,но с равными сторонами,следовательно S квадрата=а*а или «а» в квадрате. И,чтобы найти S треугольника нужно умножить половину его основания(а) на высоту(h)(S=12a*h)

Виталий Чер
[5.8K]

5 лет назад

Площадь это поверхность какого либо предмета, к примеру площадь прямоугольника находится по следующей формуле: a*b-где a,b -стороны (длина и ширина), квадрата a^2, круга ПR^2-где П-3,14 а R-радиус, конуса ПR(l+R)-где l-длина конуса и т.д.

СТЭЛС
[309K]

более года назад

Площадь это характеристика плоскости, выраженная в числовом виде. Вторично выражает размеры этой фигуры.

Площадь прямоугольника, находится путем умножения его ширины на его длину, выраженные в единых мерах.

Знаете ответ?

Источник

Загрузить PDF

Существует множество различных геометрических фигур и множество причин для того, чтобы найти их площадь. Прочитайте эту статью, если вы делаете домашнее задание по геометрии или просто хотите выяснить количество краски для ремонта комнаты.

1
Измерьте длину и ширину фигуры. Другими словами, найдите значения двух смежных сторон фигуры.^[1]
- В параллелограмме измерьте высоту и сторону, на которую опущена высота.
- В геометрической задаче значения сторон, как правило, даны. В повседневной жизни стороны необходимо замерить.
2
Перемножьте значения сторон, и вы найдете площадь. Например, чтобы найти площадь прямоугольника со сторонами 16 см и 42 см, нужно умножить 16 на 42.^[2]
- В параллелограмме перемножьте высоту и сторону, на которую опущена высота.
- Для вычисления площади квадрата вы можете возвести одну из его сторон в квадрат. Для этого можно воспользоваться калькулятором: для этого сначала нажмите нужное число, а затем клавишу, отвечающую за возведение числа в квадрат (на многих калькуляторах это x²).
3
Запишите ответ с единицами измерения. Площадь измеряется в квадратных сантиметрах (метрах, километрах и так далее.). Таким образом, площадь прямоугольника равна 672 квадратных сантиметра.
- Нередко в задачах квадрат числа приводится так: x².
Реклама

1
Найдите значения верхнего и нижнего оснований трапеции, а также ее высоты. Основания — две параллельные стороны трапеции; высота — отрезок, расположенный перпендикулярно к основаниям трапеции.^[3]
- В геометрической задаче значения сторон, как правило, даны. В повседневной жизни стороны необходимо замерить.
2

Сложите верхнее и нижнее основания. Например, дана трапеция с основаниями 5 см и 7 см и высотой 6 см. Сумма оснований равна 12 см.
3

Умножьте результат на 1/2. В нашем примере вы получите 6.
4

Умножьте результат на высоту. В нашем примере вы получите 36 — это и есть площадь трапеции.^[4]
5

Запишите ответ. Площадь трапеции равна 36 кв. см.

Реклама

1
Найдите радиус окружности. Это отрезок, соединяющий центр окружности и любую точку на окружности. Вы также можете найти радиус, разделив диаметр круга пополам.^[5]
- В геометрической задаче значение радиуса или диаметра, как правило, даны. В повседневной жизни их необходимо замерить.
2

Возведите радиус в квадрат (умножьте самого на себя). Например, радиус равен 8 см. Тогда квадрат радиуса равен 64.
3

Умножьте результат на Пи. Пи (π) – это постоянная величина, равная 3,14159. В нашем примере получим 201,06176 — это и есть площадь круга.^[6]
4

Запишите ответ. Площадь круга равна 201,06176 кв. см.

Реклама

1
Используйте данные задачи. Сектор — это часть круга, ограниченная двумя радиусами и дугой. Для вычисления его площади необходимо знать радиус окружности и центральный угол. Например: радиус равен 14 см, а угол 60°.^[7]
- В геометрической задаче начальные данные, как правило, даны. В повседневной жизни их необходимо замерить.
2

Возведите радиус в квадрат (умножьте самого на себя). В нашем примере квадрат радиуса равен 196 (14×14).
3

Умножьте результат на Пи. Пи (π) — это постоянная величина, равная 3,14159. В нашем примере получим 615,75164.^[8]
4

Разделите центральный угол на 360. В нашем примере центральный угол равен 60 градусам, в итоге получим 0,166.
5

Умножьте этот результат (деление угла на 360 ) на результат, полученный ранее (произведение пи на квадрат радиуса). В нашем примере вы получите 102,214 — это и есть площадь сектора.
6

Запишите ответ. Площадь сектора равна 102,214 кв. см.

Реклама

1
Используйте начальные данные. Для вычисления площади эллипса нужно знать большую полуось и малую полуось эллипса (то есть половины осей эллипса). Полуоси — это отрезки, проведённые из центра эллипса к его вершинам на большой и малой осях. Полуоси образуют прямой угол.^[9]
- В геометрической задаче начальные данные, как правило, даны. В повседневной жизни их необходимо замерить.
2

Перемножьте полуоси. Например, оси эллипса равны 6 см и 4 см. Таким образом, полуоси эллипса равны 3 см и 2 см. Перемножьте полуоси и получите 6.
3

Умножьте результат на пи. Пи (π) — это постоянная величина, равная 3,14159. В нашем примере получим 18,84954 — это и есть площадь эллипса.
4

Запишите ответ. Площадь эллипса равна 18,84954 кв. см.

Реклама

1
Найдите значения высоты треугольника и стороны, на которую опущена эта высота. Например, высота треугольника равна 1 м, а сторона, на которую опущена высота, равна 3 м.^[10]
- В геометрической задаче начальные данные, как правило, даны. В повседневной жизни их необходимо замерить.
2

Перемножьте высоту и сторону. В нашем примере вы получите 3.^[11]
3

Умножьте результат на 1/2. В нашем примере вы получите 1,5 — это и есть площадь треугольника.
4

Запишите ответ. Площадь треугольника равна 1,5 кв. м.

Реклама

1
Для вычисления площади фигуры сложной формы разбейте ее на несколько стандартных фигур, вычислите площадь каждой из них и сложите результаты. В геометрической задаче это легко сделать, но в повседневной жизни вам, скорее всего, придется разбить фигуру сложной формы на множество стандартных фигур.^[12]
- Начните с поиска прямых углов и параллельных линий. Они послужат в качестве основ для стандартных фигур.
2

Вычислить площадь каждой стандартной фигуры, применив вышеописанные методы.
3

Сложите найденные площади. Так вы вычислите площадь фигуры сложной формы.
4

Используйте альтернативные методы. Например, к фигуре сложной формы пририсуйте «воображаемую» фигуру, которая превратит фигуру сложной формы в стандартную фигуру. Найдите площадь такой стандартной фигуры, а затем вычтите из нее площадь «воображаемой» фигуры. Вы найдете площадь фигуры сложной формы.

Реклама

Советы

Воспользуйтесь этим калькулятором площадей, если вам нужна помощь или вы хотите посмотреть на процесс вычислений.
Если вам нужна помощь, попросите ее у человека, разбирающегося в геометрии.

Предупреждения

Убедитесь, что в вычислениях принимают участие величины, измеренные в одних единицах (например, только в сантиметрах, или только в метрах и так далее).
Всегда проверяйте ответ!

Об этой статье

Эту страницу просматривали 106 845 раз.

Была ли эта статья полезной?

Источник

p =	a + b + c	— полупериметр треугольника.
2

p =	a + b + c + d	— полупериметр трапеции.
2

S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
\|a — b\|

Формулы площади геометрических фигур

Формулы площади треугольника

Формула Герона

Формулы площади квадрата

Формула площади прямоугольника

Формулы площади параллелограмма

Формулы площади ромба

Формулы площади трапеции

Формулы площади выпуклого четырехугольника

Формулы площади круга

Формулы площади эллипса

Площадь квадрата

Площадь прямоугольника

Площадь сложных фигур

Ваши комментарии

Советы

Предупреждения

Об этой статье

Была ли эта статья полезной?

Не пропустите также: