{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат — четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
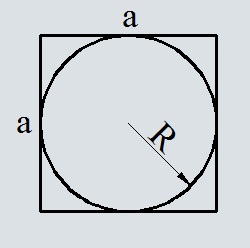
Формула площади квадрата через сторону
S = a ^2
a — сторона квадрата
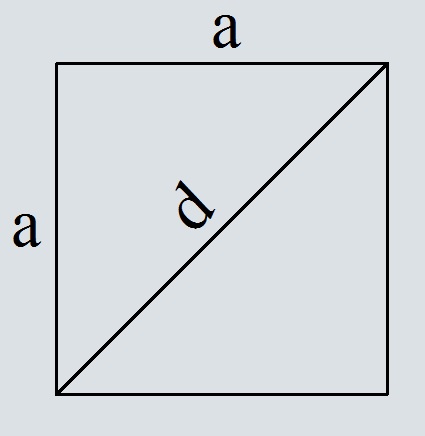
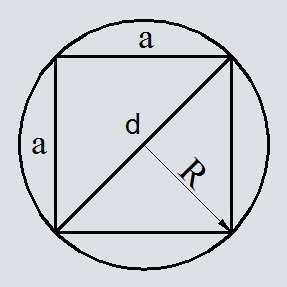
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d — диагональ квадрата
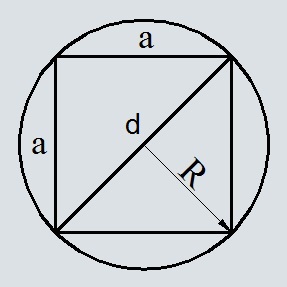
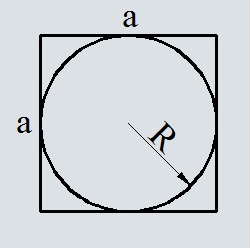
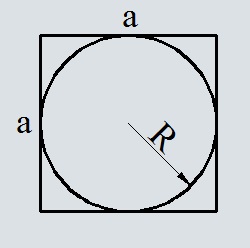
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r — радиус вписанной окружности
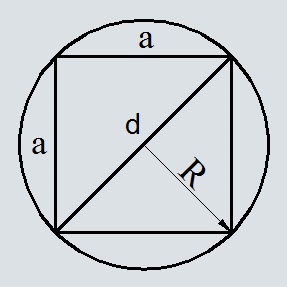
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R — радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P — периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
Квадрат – это геометрическая фигура; правильный четырехугольник, т.е. четырехугольник, имеющий равные стороны и углы (90°).
- Формула вычисления площади
- Примеры задач
Формула вычисления площади
1. По длине стороны:
Площадь квадрата (S) равняется квадрату длины его стороны:
S = a2
Данная формула следует из того, что квадрат является частным случаем прямоугольника, площадь которого находится путем умножения его смежных сторон:
S = a*b
А т.к. все стороны квадрата равны, то вместо стороны b мы снова подставляем в формулу сторону a, т.е. S = a*a = a2.
2. По по длине диагонали
Площадь квадрата равняется половине квадрата длины его диагонали:
S = d2/2
Соотношение стороны и диагонали квадрата: d=a√2.
Примеры задач
Задание 1
Найдите площадь квадрата, сторона которого равна 7 см.
Решение:
Используем формулу по длине стороны, т.е. S = 72 = 49 см2.
Задание 2
Найдите площадь квадрата, диагональ которого равняется 4 см.
Решение 1:
Воспользуемся второй формулой (по длине диагонали): S = 42/2 = 8 см2.
Решение 2:
Мы можем выразить длину стороны через диагональ: a = 4/√2. И тогда, используя первую формулу, S = (4/√2)2 = 8 см2.
- Площадь квадрата по стороне
- Площадь квадрата по диагонали
- Площадь квадрата по периметру
- Площадь квадрата по радиусу описанной окружности
- Площадь квадрата по радиусу вписанной окружности
- Площадь квадрата вписанного в окружность, по известной длине окружности
- Площадь квадрата вписанного в окружность, по известной площади окружности
- Площадь квадрата через длину окружности, вписанной в этот квадрат
- Площадь квадрата через площадь окружности, вписанной в этот квадрат
Площадь квадрата по стороне
Формула площади квадрата по стороне
Где S — площадь квадрата,
a — сторона квадрата
Площадь квадрата по диагонали
Формула площади квадрата по диагонали
Где S — площадь квадрата,
d — диагональ квадрата
Площадь квадрата по периметру
Формула площади квадрата по периметру
Где S — площадь квадрата,
P — периметр квадрата
Площадь квадрата по радиусу описанной окружности
Формула площади квадрата по радиусу описанной окружности
Где S — площадь квадрата,
R — радиус описанной окружности
Площадь квадрата по радиусу вписанной окружности
Формула площади квадрата по радиусу вписанной окружности
Где S — площадь квадрата,
R — радиус вписанной окружности
Площадь квадрата вписанного в окружность по известной длине этой окружности
Введите длину окружности l
Формула площади квадрата вписанного в окружность по известной длине этой окружности
Где S — площадь квадрата,
l — длина окружности
Площадь квадрата вписанного в окружность по известной площади этой окружности
Введите площадь окружности Sокр
Формула площади квадрата вписанного в окружность по известной площади этой окружности
Где S — площадь квадрата,
Sокр — площадь окружности
Площадь квадрата через длину окружности вписанной в этот квадрат
Введите длину окружности l
Формула площади квадрата через длину окружности вписанной в этот квадрат
Где S — площадь квадрата,
l — длина окружности
Площадь квадрата через площадь окружности вписанной в этот квадрат
Введите площадь окружности Sокр
Формула площади квадрата через площадь окружности вписанной в этот квадрат
Где S — площадь квадрата,
Sокр — площадь окружности
Площадь квадрата можно найти с помощью двух основных формул:
1) Через сторону.
2) Через диагональ.
Как найти площадь квадрата, если известна его сторона.
Как известно, квадрат — это частный случай прямоугольника, у которого все стороны равны.
Площадь прямоугольника равна произведению 2 его сторон:
Sпр = a * b, a и b — стороны прямоугольника.
В случае с квадратом a = b.
Таким образом, площадь квадрата будет находиться по формуле:
Sкв = a².
Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².
Как найти площадь квадрата, если известна его диагональ.
Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата — катетами.
Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:
a*a + b*b = c*c.
a и b — катеты, c — гипотенуза.
В нашем случае a = b, а гипотенуза — это диагональ d.
Перепишем формулу в виде:
2a² = d².
a² = d² / 2.
Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.
Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².
- Главная
- Справочник
- Как найти площадь квадрата
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь квадрата
Поможем сделать домашку Online
Первое занятие бесплатно
Перейти
Решение задачи по геометрии
Выполнение 1-3 дня
от 150 ₽
Заказать
Подробнее
Контрольные по геометрии
Выполнение 1–4 дня
от 310 ₽
Заказать
Подробнее
Контрольные по математике
Выполнение 1–4 дня
от 260 ₽
Заказать
Подробнее
Содержание:
- Формула
- Примеры вычисления площади квадрата
Формула
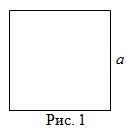
Чтобы найти площадь квадрата (рис. 1), надо длину его стороны возвести в квадрат, то есть
$$S=a^2$$
Напомним, что квадратом называется правильный четырехугольник, у которого все стороны и все углы равны.
Примеры вычисления площади квадрата
Пример
Задание. Найти площадь квадрата со стороной 3 см.
Решение. Площадь квадрата равна квадрату его стороны, то есть
$S=3^2=9$(см2)
Ответ. $S=3^2=9$ (см2)
Все формулы площади
Калькулятор площади квадрата

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Узнать стоимость
Пример
Задание. Найти площадь квадрата, диагональ которого равна 2 м.
Решение. Известно, что сторона
$a$ квадрата связана с его диагональю $d$ соотношением:
$$d=a sqrt{2}$$
тогда отсюда находим, что
$a=frac{d}{sqrt{2}}=frac{2}{sqrt{2}}=sqrt{2}$(м)
А тогда искомая площадь
$S=(sqrt{2})^{2}=2$ (м2)
Ответ. $S=2$ (м2)
Читать дальше: как найти площадь прямоугольника.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела «Как найти площадь»

Поможем выполнить
любую работу
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Контрольные, курсовые, дипломные
Узнать подробнее
Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Краткая теория
- Формулы
- Теоремы
- Свойства
- Таблицы
Теоретический материал
- Формулы и свойства логарифмов
- Таблица интегралов
- Тригонометрические формулы
- Таблица степеней
- Формулы и свойства степеней
- Формулы площади
- Таблица Лапласа
- Формулы объема
Все еще сложно?
Наши эксперты помогут разобраться
Все услуги
Дипломные работы
Выполнение 2-3 недели
от 7000 ₽
Курсовые работы
Выполнение 5-7 дней
от 1500 ₽
Контрольные работы
Выполнение 1–4 дня
от 260 ₽
Написание рефератов
Выполнение 2-5 дней
от 650 ₽
Решение задач
Выполнение 1–3 дня
от 90 ₽
Написание диссертаций
Выполнение 2-3 месяца
от 19 000 ₽
Как найти площадь треугольника
Как найти площадь
Как найти площадь ромба
Как найти площадь прямоугольного треугольника
Не получается написать работу самому?
Доверь это кандидату наук!
Я даю согласие на обработку своих персональных данных в соответствии с Политикой
конфиденциальности и принимаю условия Договора публичной оферты
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
Прикрепить файл
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные