Добавил:
Вуз:
Предмет:
Файл:
Скачиваний:
455
Добавлен:
24.07.2017
Размер:
2.77 Mб
Скачать
Кроме геометрических параметров самолета
для определения аэродинамических
характеристик необходимо рассчитать
ряд относительных геометрических
характеристик частей самолета.
Так, для фюзеляжа необходимо рассчитать
следующие относительные геометрические
параметры:
-
удлинение фюзеляжа
;
-
удлинение носовой части
;
-
удлинение цилиндрической части
;
-
удлинение кормовой части
;
-
сужение носовой части
-
сужение кормовой части
Для несущей поверхности необходимо
рассчитать следующие относительные
геометрические параметры:
-
удлинение несущей поверхности (крыло,
ГО)
;
-
удлинение консоли несущей поверхности
(крыло, ГО)
;
-
удлинение ВО
-
удлинение консоли ВО
-
Р
ис.
4.4. Определение САХ трапециевидного
крыла и координаты ее носкасужение несущей поверхности
;
-
среднюю аэродинамическую хорду несущей
поверхности
.
формы в плане
Для крыла простой формы в плане САХ и
координаты ее носка (рис. 4.4.) можно
рассчитать по формулам:
В итоге получим следующие параметры
самолета:
-
Крыло
Площадь базового крыла
Размах базового крыла
Удлинение базового крыла
Центральная хорда крыла
САХ крыла
Координата начала САХ
Сужение крыла
Изолированные консоли крыла
Площадь консолей крыла
Размах консолей крыла
Бортовая хорда крыла
Концевая хорда крыла
САХ консолей крыла
Координата начала САХ консоли крыла
Удлинение консоли крыла
Сужение консоли крыла
Угол стреловидности передней кромки
крылаУгол стреловидности задней кромки
крылаУгол стреловидности по линии 1/2 хорд
крылаОтносительная
толщина профиля крылаSкр=
13502966 мм2lкр= 8216
ммλкр= 5
b0= 2422 мм
bA= 1766 мм
xA= 807 мм
ηкр= 2,8
Sккр=
10879692 мм2lккр= 7083
ммb0ккр=
2207 ммbккр= 865
ммbAккр= 1634 мм
xAккр= 705 мм
λккр= 4,61
ηккр= 2,55
χпккр= 25°
χзккр= 5°
χ0,5 кр= 15°
Горизонтальное оперение
Площадь ГО с подфюзеляжной частью
Размах ГО с подфюзеляжной частью
Удлинение ГО
Сужение ГО
Центральная хорда ГО
САХ ГО
Координата начала САХ ГО
Изолированные консоли ГО
Площадь консолей ГО
Размах консолей ГО
Бортовая хорда ГО
Концевая хорда ГО
САХ консолей ГО
Координата начала САХ консоли ГО
Удлинение консоли ГО
Сужение консоли ГО
Угол стреловидности передней кромки
ГОУгол стреловидности задней кромки
ГОУгол стреловидности по линии 1/2 хорд
ГООтносительная
толщина профиля ГОSГО=
3812000 мм2lГО= 4000
ммλГО= 4,20
ηГО= 2,48
b0ГО= 1358
ммbAГО= 1012 мм
xAГО= 455 мм
SкГО=
2688333 мм2LкГО= 3114
ммb0кГО=
1179 ммbкГО= 548
ммbAкГО= 902 мм
xAкГО= 364 мм
λкГО= 3,61
ηкГО= 2,15
χпкГО= 28°
χзкГО= 7°
χ0,5 ГО= 18°
Вертикальное оперение
Площадь ВО с фюзеляжной частью
Высота ВО с фюзеляжной частью
Удлинение ВО
Сужение ВО
Центральная хорда ВО
САХ ВО
Координата начала
САХ ВОSВО=
3672449 мм2lВО= 2453
ммλВО= 3,28
ηВО= 2,84
b0ВО= 2215
ммbAВО= 1612 мм
xAВО= 927 мм
Изолированные консоли ВО
Площадь консоли ВО
Высота консоли ВО
Бортовая хорда ВО
Концевая хорда ВО
САХ консоли ВО
Координата начала САХ консоли ВО
Удлинение консоли ВО
Сужение консоли ВО
Угол стреловидности передней кромки
ВОУгол стреловидности задней кромки
ВОУгол стреловидности по линии 1/2 хорд
ВООтносительная
толщина профиля ВОSкВО=
2513438 мм2lкВО= 1887
ммb0кВО=
1884 ммbкВО= 780
ммbAкВО= 1408 мм
xAкВО= 732 мм
λкВО= 2,83
ηкВО= 2,42
χпкВО= 42°
χзкВО= 18°
χ0,5 ВО= 31°
Фюзеляж
Длина
Максимальный
диаметр фюзеляжаПлощадь
миделевого сеченияДлина
носовой частиДлина
цилиндрической частиДлина
кормовой частиДиаметр
носовой частиДиаметр
кормовой частиУдлинение
фюзеляжаУдлинение
носовой частиУдлинение
цилиндрической частиУдлинение
кормовой частиСужение
носовой частиСужение кормовой
частиLф= 10300 мм
dф= 1390 мм
Sф= 1517468
мм2Lнос= 3355
ммLцил= 4637
ммLкорм=
2308 ммdнос= 0 мм
dкорм=
760 ммλф= 7,41
λнос= 2,41
λцил= 3,34
λкорм= 1,66
ηнос= 0
ηкорм= 0,55
Соседние файлы в папке Текст
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
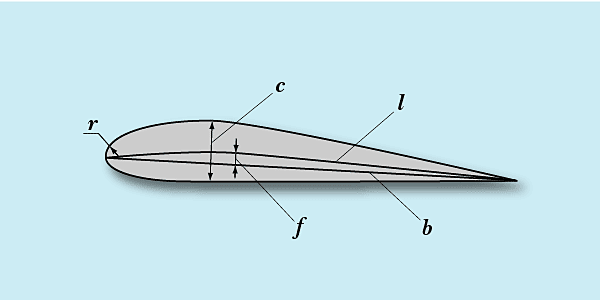
Enter the wingspan and the chord into the calculator to determine the total wing area. If calculating a tapered wing, the root chord and tip chord will be required.
- Lift Force Calculator
- Wind Pressure & Force Calculator
- Glide Ratio Calculator
- Drag Equation Calculator (Drag Force Calculator)
- Wing Volume Calculator
- Top Chord Length Calculator
Wing Area Formulas
The following two formulas are used to calculate the wing areas of a triangle and tapered (trapezoidal) wings.
- Where WA is the wing area of a triangle wing
- WS is the wing span
- RC is the roots chord
Or, for trapezoidal wings:
- Where RC is the root chord
- TC is the tip chord
- WS is the wingspan
Wing Area Definition
What is wing area?
A wing area, also known as wing surface area, is defined as the total 2-dimensional space taken up by a wing shape. These shapes are most commonly triangle or trapezoidal shapes, but can also be by rectangular, or irregular shapes.
Example Problem
How to calculate wing area?
The following example outlines the steps to calculate a wing area of a trapezoidal wing.
First, determine the root chord. This should be the longer of the two chords and in this case is 3 feet.
Next, determine the tip chord. The smaller of the two chords in this case is 2 feet.
Next, determine the wing span. The length of the wing is measured to be 6 feet.
Finally, calculate the wing area using the formula above:
WA = (RC + TC) / 2 * WS
WA = (3+ 2) / 2 * 6
WA = 15 ft^2
Приветствую коллег!
Возник вопрос о вычислении площади крыла.
Что такое площадь вообще, я знаю из школьного учебника математики (геометрия).
Как вычислять площадь сложных фигур я тоже в курсе — разбиваем сложную фигуру на более простые, вычисляем площадь каждой и суммируем.
А как же вычеслять площадь крыла, ведь оно объемно?
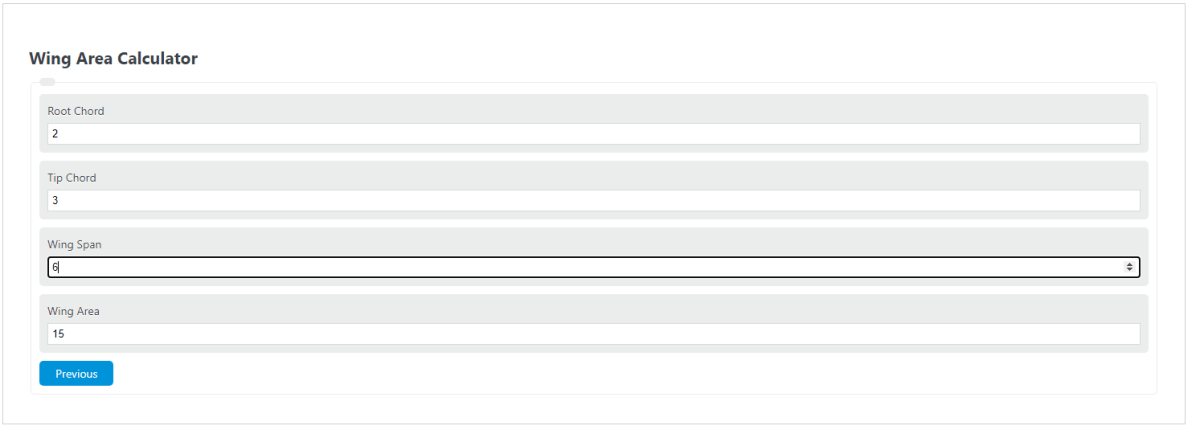
Я могу вычислить площадь нижней поверхности, могу вычислить площадь и верхней поверхности, могу вычислить и площадь по хорде “b” (Рисунок ниже).
Какую из них подставлять в формулу расчета подъемной силы крыла:
Y= Cy* p*V 2*S/2
По-моему было бы ошибкой подставлять в чистом виде любое из трех вычислений,т.к. все три значения могут быть не связаны между собой.
Или все же по средней линии профиля “l”, равноудаленной от верхней и нижней образующих профиля?
Если да, то почему об этом не пишут?
Спасибо.
Если да, то почему об этом не пишут?
Потому, что берётся площадь крыла в плане. (вид сверху)
Потому, что берётся площадь крыла в плане. (вид сверху)
А площадь в плане с учетом угла атаки или нет?
:)Шутка:) А если крыло V образное?
Потому, что берётся площадь крыла в плане. (вид сверху)
Но ведь тогда получается ерунда.
“В плане” — вид сверху, площадь может оставаться неизменной, а реально профиль будет изменен.
Вот например как на рисунках ниже.
Здесь мы видим, что на рис.2 верхняя огибающая крыла длиннее, чем на рис.1 (нижняя часть крыла осталась без изменений, как и хорда).
Т.е. “в плане”, глядя сверху, изменений нет, из чего следует, что и значения в формуле не поменялись, а значит и подъемная сила крыла.
Но профиль-то изменился и поток воздуха над верхней кромкой рис.2 движется быстрее, чем над верхней кромкой рис.1, т.к. потоку надо пройти бОльшее расстояние за тот же период времени.
А раз поток движется быстрее, то значит и подъемная сила выше.
Именно этот ньюанс и не отражен в формуле. Значит должен быть еще и другой расчет, учитывающий этот момент.
А если крыло V образное?
Высчитывайте площадь, а дальше по формуле, если она конечно полностью отражает расчет, в чем я сомневаюсь.
Про другие части формулы не забываем?
У каждого профиля свой Сy — поэтому площадь — “в плане”
а про Су почему забыли?
который, кстати, является функцией от угла атаки…
ПыСы… сомневаетесь — пользуйтесь “панельными методами” … 😃))
Про другие части формулы не забываем?
У каждого профиля свой Сy — поэтому площадь — “в плане”
А как это Су вычислять?
А как это Су вычислять?
Никак, это есть величина, полученная в результате продува профиля… зависящая от угла атаки…
ну почему-же… 😃
опять-же вспомним про панельные методы… 😃
но для ПРАКТИЧЕСКОГО применения существуют справочники и атласы профилей…
где их характеристики и указаны…
Неужели все так безнадежно.
Меня собственно интересует как определять подъемную силу в зависимости от разности площади верхней и нижней площади крыла.
Например на рисунках выше, нижняя площадь крыла 50 кв.см. (У обоих крыльев.!!!)
На рис.1 верхняя площадь 60 кв.см.
В итоге имеем, что верхняя площадь больше нижней на 10кв.см или на 20%
На рис.2 верхняя площадь 75 кв.см.
В итоге имеем, что верхняя площадь больше нижней на 25кв.см или на 50%
Если сравнивать верхние площади обоих крыльев, то у крыла на рис.2 она больше чем у крыла на рис.1 на 15кв.см или если в процентах, то на 25% (15 является четвертью значения 60).
Хочется выяснить на сколько или во сколько раз увеличится подъемная сила крыла при увеличении верхней площади например на 25% или 50%.
Как бы это посчитать?
Пока не будем говорить о том, что будет работать такое крыло или нет.
Задача стоит в методе расчета.
Меня собственно интересует как определять подъемную силу в зависимости от разности площади верхней и нижней площади крыла.
Бред
ТАК не посчитаете…
хотя-бы потому, что:
1- при одинаковой разнице площадей профили могут иметь разный Су по альфа…
2- набегающий поток НЕ приходит в точку (0,0) на носике профиля… даже на нулевом угле атаки (кроме симметричных при альфе=0). как разницу считать будете?
ещё раз повторюсь… ищите в Атласе Ваш профиль и будет Вам…
Бред
Спасибо за коммплимент.
ТАК не посчитаете…
хотя-бы потому, что:
1- при одинаковой разнице площадей профили могут иметь разный Су по альфа…
2- набегающий поток НЕ приходит в точку (0,0) на носике профиля… даже на нулевом угле атаки (кроме симметричных при альфе=0). как разницу считать будете?..
Именно нулевой угол атаки и имеется ввиду.
ТАК
ещё раз повторюсь… ищите в Атласе Ваш профиль и будет Вам…
А где можно на этот атлас взглянуть?
Именно нулевой угол атаки и имеется ввиду.
А где можно на этот атлас взглянуть?
А это ничего не меняет… точка, где потоки разделяются на верхний и нижний, всё-равно будет смещена на нижнюю поверхность крыла
Атлас где искать? 😂
ну я нашёл секунд за 10…
Так… Теперь моя очередь… На настоящих самолётах число Рейнольдса в десятки тысяч раз больше, чем на их моделях-копиях. Попытки скопировать профиль крыла, как правило ни к какому положительному результату не приводят, самолёт получается очень чувствительный к центровке (особенно, если сужение крыла превышает 2), т.к. пока корневые части крыла уже в состоянии удерживать самолёт в воздухе, то концы крыла, как наиболее узкие части, ещё не создают надлежащей подъёмной силы и по сути выполняют роль аэродинамических законцовок Уиткомба (как на всех современных пассажирских самолётах, только там они установлены почти под 90град.) и на этой скорости поток на них не лежит, на этих участках крыла происходит срыв потока до тех пор, пока модель не наберёт минимально возможную, для такой ширины крыла и при такой нагрузке, скорость.
Если сравнивать разные типы моделей-копий, то можно сделать следующий вывод: Число Рейнольдса для копии пилотажки, будет больше чем для копии пассажирского самолёта такого же размера — т.е. пилотажка летит “быстрее”.
Далее, профиль крыла современного гражданского самолёта сверхкритический, с небольшой вогнутостью на нижней части профиля у хвостика. Неужели там такая дикая нагрузка на крыло? Или это сделано для снижения посадочной скорости? Применение сверхкритического профиля на модели ничего не даёт, кроме большей максимальной скорости. Пробовал. В плане борьбы с ранним концевым срывом, наиболее эффективна аэродинамическая (с помощью разных профилей в корне и на конце крыла) и геометрическая крутка крыла. Последняя позволяет уменьшить посадочную скорость в 1,5…2 раза в зависимости от нагрузки на крыло. Вопрос: если не далать из копии “летающий кирпич”, может стоит применять профиль крыла от планера? Он чем-то похож на профиль настоящего крыла.
Сильно не пинайте, я в профилях ни бум-бум, строить профиль по понятиям, тоже не хочу — ни разу не помогло. Ещё вопрос: если на модели сделать отклоняемые предкрылки, улучшатся ли взлётно-посадочные свойства крыла? Если да, то насколько.
На всех моделях гражданских самолётов, построенных мной за последнее время нагрузка на крыло прим. 100гр/ кв дм, размах 1900…2000мм.
Может кто-нибудь посоветует что-нибудь толковое?
Применение сверхкритического профиля на модели ничего не даёт, кроме большей максимальной скорости.
Будете смеяться, но именно для этого сверхкритические профиля и сделаны…
чтобы сдвинуть критическое число М максимально дальше…
там ведь не только поджатие в конце нижней поверхности, но и более плоская верхняя часть, может и максимальная толщина профиля сдвинута дальше от носка (давно дело было). Если глянуть распределение давления по хорде такого профиля, то на верхней поверхности, где собсно и садится локальный скачок уплотнения, увидим “полочку”…
про планерные профили ничего не посоветую, увы… с прошлого тысячелетия не занимался этим делом… шклероз, знаете-ли 😦
ПыСы… но, думаю, попробовать стоит… тока не брать чисто ламинарный…
ПыПыСы… предкрылок и щелевой закрылок вещь тонкая, как Восток…
Требует расчёта и, естессно, точного исполнения.
ПыПыСы… предкрылок и щелевой закрылок вещь тонкая, как Восток…
Требует расчёта и, естессно, точного исполнения.
Уже на 3-й по счёту модели применяю вот такие закрылки:
Работает как положено. Если сравнивать с флаперонами, то флапероны вызывают преждевременный срыв потока и самолёт валится. Бывает насмерть.
-Щель,образующаяся при выпуске закрылков,на всем ее протяжении должна быть СУЖАЮЩЕЙСЯ — это ключевой момент при проектировании щелевого закрылка.
копи-паст отсюда… delta.wtr.ru/archive/9113.html
про необходимость отделения мух(элеронов) от котлет(закрылков) согласен полностью
На всех моделях гражданских самолётов, построенных мной за последнее время нагрузка на крыло прим. 100гр/ кв дм, размах 1900…2000мм.
Может кто-нибудь посоветует что-нибудь толковое?
Думаю, все проще. Если сделаете нагрузку поменьше, то все проблемы пропадут, так как потребные улы атаки уменьшатся. А доведете нагрузку до 25 г/кв дм, так и петли делать сможете.
Вы уже добились таких данных?
Вы уже добились таких данных?
Это была моя первая ошибка, я сделал все очень старательно и красиво, а о весе не подумал.
Самолет взлетел, но полетом бы я это не назвал.
После этого понял, что самолет должен быть как можно легче, тогда он будет летать на малых углах атаки и многие проблемы этим будут сняты (чувствительность к профилю крыла, потеря подъемной силы на концах сужающегося крыла).
Как и на чем снизить вес я Вам не посоветую, это надо конкретно работать над предполагаемой конструкцией и иметь некоторый опыт или статистику по подобным конструкциям.
Увидите хорошо летающий самолет, расмотрите как он сделан, расспросите о деталях конструкции, перенимайте опыт, добавляйте свои идеи.
Хорошо бы познакомиться с расчетами на прочность, это поможет определить минимальные размеры деталей, а также создавать более эффективные в весовом отношении конструкции.
Да, уж… Всё это хорошо, только боюсь не увижу при жизни модель грузовика с размахом 2м и нагрузкой 55гр/ кв дм.
Мои модели с выше указанной нагрузкой на крыло летают красиво, неспеша — скорость полёта около 65…70 км/ч.
Вес… Из современных доступных материалов, без применения сложных технологий, не в ущерб красоте, вряд ли получится сделать легче. Какой бы лёгкий самолёт ни был, ему требуется профиль крыла, приспособленный под его нормальную полётную скорость. Расчитать прочность отдельных элементов самолёта не сложно. Достаточно простейших знаний по теории сопротивления материалов.
Зададимся задачей: модель Ан 72rcopen.com/forum/f7/topic137456; Плошадь всех обшивок 127кв дм. Давайте посчитаем вес ТОЛЬКО обшивок.
Плошадь всех обшивок 127кв дм. Давайте посчитаем вес ТОЛЬКО обшивок.
В свое время, я проводил такие исследования: делал образцы типовых элементов и определял их вес. Конкретно, делал различные образцы обшивок площадью около 0.5 кв дм и анализировал их вес в зависимости от материала обшивки и покрытия.
Вес покрытия очень важен и он не маленький.
К сожалению, за давностью лет это все не сохранилось, да и материалы (лакокрасочные) уже совсем другие.
Вы могли бы таким образом поэкспериментировать и подобрать материалы и технологию, дающие наименьший вес.
Я хотел сказать, что мои эксперименты закончены. Современные материалы, такие как бальза толщ. 1мм, депроновая потолочка толщ. 4мм, Пенопласт, плотностью 25кг/куб. м, дают по итогу одну и ту же массу конструкции… Вы бы не могли привести хоть одну цифру по материалам для обшивки? Ваши советы я говорил себе сам, ещё 4 года назад…
Министерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального образования
«Южно-Уральский государственный университет»
Национальный исследовательский институт
Аэрокосмический факультет
Кафедра «Летательные аппараты и автоматические установки»
Курсовая работа
по тему:
«Расчет аэродинамических характеристик летательного аппарата»
Руководитель:
Сидельников Р.В.
_______________
Автор работы:
Малов Е. В.
группа АК-310
_______________
Аннотация
В работе приведен расчет аэродинамических характеристик ракеты заданной геометрией. Окончательные характеристики заданной ракеты приведены в таблице и в виде графиков в зависимости от числа Маха, угла атаки и высоты полета.
Оглавление
Введение. 7
Параметры торможения. 10
Коэффициент давления полного торможения. 10
Давление в точке полного торможения. 11
Температура в точке полного торможения. 11
Расчет аэродинамических характеристик фрагментов летательного аппарата 12
Притупленный конус. 12
Площадь боковой поверхности: 12
Коэффициент продольной силы от давления: 13
Коэффициент нормальной силы.. 13
Производная от коэффициента нормальной силы по углу атаки α. 13
Координата центра давления относительно теоретической вершины ЛА: 13
Цилиндр. 14
Площадь боковой поверхности: 14
Коэффициент продольной силы от давления: 14
Коэффициент нормальной силы.. 14
Производная от коэффициента нормальной силы по углу атаки α. 14
Координата центра давления: 15
Оперение ЛА.. 16
Площадь лопасти оперения в плане. 16
Производная от коэффициента нормальной силы по углу атаки изолированной лопасти оперения: 16
Производная от коэффициента нормальной силы по углу атаки оперения: 16
Коэффициент нормальной силы.. 17
Коэффициент силы продольного сопротивления от давления. 17
Координата центра давления. 17
Крылья. 17
Площадь лопасти крыла в плане. 17
Производная от коэффициента нормальной силы по α изолированной лопасти крыла 18
Производная от коэффициента нормальной силы по углу атаки крыла. 18
Коэффициент нормальной силы.. 19
Коэффициент силы продольного сопротивления от давления. 19
Координата центра давления: 19
Корпус летательного аппарата (усеченный конус + цилиндрическая часть) 20
Коэффициент нормальной силы ЛА.. 20
Производная коэффициента нормальной силы по α. 20
Коэффициент силы трения. 20
Коэффициент силы донного сопротивления. 20
Коэффициент силы продольного сопротивления. 21
Коэффициент центра давления относительно теоретической вершины корпуса 21
Коэффициент аэродинамического давления. Ошибка! Закладка не определена.
Коэффициент лобового сопротивления корпуса. 21
Коэффициент подъёмной силы корпуса. 21
Аэродинамическое качество корпуса. 22
Моментные характеристики корпуса. 22
Координата центра давления корпуса. 22
Коэффициент аэродинамического давления корпуса. 22
Коэффициент запаса статической устойчивости. 22
Коэффициент аэродинамического момента относительно центра тяжести. 22
Производная коэффициента аэродинамического момента по углу атаки α. 22
Производная коэффициента аэродинамического момента относительно центра тяжести по углу атаки α. 23
Расчёт аэродинамических коэффициентов ЛА (конус + цилиндр + оперение) 24
Коэффициент и абсолютное значение нормальной силы ЛА.. 24
Производная коэффициента нормальной силы ЛА по углы атаки. 24
Коэффициент и абсолютное значение продольной силы ЛА.. 24
Коэффициент и абсолютное значение лобового сопротивления ЛА.. 24
Коэффициент и абсолютное значение подъёмной силы ЛА.. 24
Аэродинамическое качество ЛА.. 25
Моментные характеристики ЛА: 25
Координата центра давления ЛА.. 25
Коэффициент центра давления. 25
Коэффициент аэродинамического момента. 25
Коэффициент запаса статической устойчивости. 25
Производная коэффициента аэродинамического момента относительно центра тяжести. 25
Производная коэффициента аэродинамического момента по углу атаки α. 26
Производная коэффициента аэродинамического момента относительно центра тяжести по углу атаки α. 26
Расчёт аэродинамических коэффициентов ЛА (конус + цилиндр + оперение + крыло) 27
Коэффициент и абсолютное значение нормальной силы ЛА.. 27
Производная коэффициента нормальной силы ЛА по углы атаки. 27
Коэффициент и абсолютное значение продольной силы ЛА.. 27
Коэффициент и абсолютное значение лобового сопротивления ЛА.. 27
Коэффициент и абсолютное значение подъёмной силы ЛА.. 27
Аэродинамическое качество ЛА.. 28
Моментные характеристики ЛА: 28
Координата центра давления ЛА.. 28
Коэффициент центра давления. 28
Коэффициент аэродинамического момента. 28
Коэффициент запаса статической устойчивости. 28
Коэффициент аэродинамического момента относительно центра тяжести. 28
Производная коэффициента аэродинамического момента по углу атаки α. 29
Производная коэффициента аэродинамического момента относительно центра тяжести по углу атаки α. 29
Введение
Расчет аэродинамических характеристик помогает решить многие задачи при проектировании и отработке летательного аппарата (далее по тексту ЛА), а именно:
- при выборе оптимальной аэродинамической схемы;
- при проведении баллистических расчетов, определении сил и моментов относительно центра масс при движении по траектории в плотных слоях атмосферы с изменяющейся высотой (плотностью среды), скоростью и углами атаки;
- при проведении расчетов органов управления для обеспечения требуемых управляющих усилий и моментов;
- при проведении расчетов прочности корпуса ракеты на активном участке полета при действии переменной аэродинамической нагрузки;
- при проведении расчетов прочности и разогрева ЛА, на участке спуска в плотных слоях атмосферы;
- при решении других задач, возникающих во время проектирования ЛА.
Задача определения аэродинамических характеристик ЛА является достаточно сложной, т. к. геометрические формы (внешняя геометрия) современных аппаратов далеки от элементарных (сфера, конус, цилиндр). В связи с этим возникает задача представления геометрии ЛА в более простом виде, применимом для проведения расчетов. При проведении данного расчета полагалось, что ЛА можно представить в виде набора простейших тел вращения (полусферический сегмент, цилиндр, конус усеченный) с присоединенными к ним элементами стабилизации (стабилизаторы и крылья). Такой набор составных элементов позволяет с достаточной точностью аппроксимировать внешнюю геометрию большинства современных ракет.
Целью данной работы является овладение методом приближенного аэродинамического расчета и исследование зависимости основных аэродинамических характеристик от параметров обтекающего потока, таких как угол атаки, число Маха и высота полета.
Задание для расчета
|
Вариант |
Параметры |
||||||||||
|
Корпус |
ГЧ |
Оперение |
Струя |
Крылья |
|||||||
|
26 |
1.5 |
0.746 |
9.38 |
0.836 |
2 |
0.6 |
0 |
0.8 |
4 |
0.8 |
0 |
Относительные размеры представлены в таблице 1.
Таблица 1
Таким образом, получаем абсолютные размеры в метрах указанные в таблице 2.
|
Таблица 2 |
|||||||||||
|
Вариант |
Параметры |
||||||||||
|
Корпус |
ГЧ |
Оперение |
Струя |
Крылья |
|||||||
|
26 |
1,5 |
14.07 |
10,5 |
3,135 |
3 |
0,9 |
0 |
1,2 |
6 |
1,2 |
0 |
r= 0,225 – радиус затупления конуса;
= 3,023 – длина притупленного конуса;
– угол полураствора конуса (рассчитан с помощью встроенной функции приложения «КОМПАС-3D V13» — измерить угол).
Дополнительные данные: ; H=10 км; М=0,3
Координата центра тяжести ЛА вычислена как координата центра объема ЛА (при ) пренебрегая объемами крыльев и оперения и равна =7.38 м.
;
;
(м3);
(м3);
(м);
(м);
(м);
Для воздуха k=1,4.
По соответствующим таблицам находим параметры атмосфера на высоте H=10 км [1]:
— плотность на высоте 10 км;
К – температура на высоте 10 км;
Па – давление на высоте 10 км;
– кинематическая вязкость потока на высоте 10 км;
м/сек – скорость звука на высоте 10 км;
Число Рейнольдса:
для 0,3:
Параметры торможения
Коэффициент давления полного торможения
Для дозвуковых скоростей полета:
при 0,3:
Давление в точке полного торможения
Скорость набегающего потока:
;
Скоростной напор:
;
Давление в точке полного торможения:
;
при 0,3:
м/c;
;
Па;
Температура в точке полного торможения
Температура в точке полного торможения находится по формуле:
.
при 0,3:
К.
Расчет аэродинамических характеристик фрагментов летательного аппарата
За характерную площадь примем площадь крыльев в плане, включая подфюзеляжную часть.
( )
Рисунок 2 – Аэродинамическая схема притупленного конуса ЛА
Притупленный конус
Имеем, что .
Площадь боковой поверхности:
где м
;
Коэффициент продольной силы от давления:
при =0,3
;
где
Коэффициент нормальной силы
при =0,3:
;
Производная от коэффициента нормальной силы по углу атаки α
при =0,3:
;
Координата центра давления относительно теоретической вершины ЛА:
=2.929 м,
где
м
м;
А – расстояние от начала притупленного конуса до теоретической вершины ЛА.
Имеем, что А= .
Рисунок 3 – Аэродинамическая схема цилиндрической части ЛА
Цилиндр
Площадь боковой поверхности:
Коэффициент продольной силы от давления:
;
Коэффициент нормальной силы
при =0,3:
;
Производная от коэффициента нормальной силы по углу атаки α
при =0,3:
;
Координата центра давления:
здесь – расстояние от начала цилиндра до теоретической вершины ЛА.
Имеем, что =3.135 (м);
м.
Оперение ЛА
Площадь лопасти оперения в плане
(м2);
где М – размах одной лопасти;
м – удлинение оперения;
– относительная площадь оперения;
Производная от коэффициента нормальной силы по углу атаки изолированной лопасти оперения:
для =0,3:
=0.146;
Производная от коэффициента нормальной силы по углу атаки оперения:
для =0,3:
;
Где k=3 – количество лопастей оперения
θi – угол отклонения от вертикали;
Коэффициент нормальной силы
при =0,3:
;
Коэффициент силы продольного сопротивления от давления
при =0,3:
;
где
;
Координата центра давления
м;
Где — расстояние от задней кромки лопастей оперения до теоретической вершины ЛА. Для нашего случая м.
Крылья
Площадь лопасти крыла в плане
=2.7;
где
м – размах одной лопасти;
м – удлинение лопасти крыла;
м2 – относительная площадь крыла;
Производная от коэффициента нормальной силы по α изолированной лопасти крыла
при =0,3:
=0.997;
Производная от коэффициента нормальной силы по углу атаки крыла
=0,3:
Где k=2 – количество лопастей крыла,
θ – угол отклонения от вертикали.
=1.993;
Коэффициент нормальной силы
при =0,3:
;
Коэффициент силы продольного сопротивления от давления
при =0,3:
=0.012;
где
;
Координата центра давления:
м;
где м;
Корпус летательного аппарата (усеченный конус + цилиндрическая часть)
Коэффициент нормальной силы ЛА
при =0,3:
;
Н;
Производная коэффициента нормальной силы по α
при =0,3:
;
где ;
Коэффициент силы трения
при =0,3:
;
Коэффициент силы донного сопротивления
для =0,3:
;
Где
Коэффициент силы продольного сопротивления
при =0,3:
;
где
;
— коэффициент, учитывающий форму ЛА;
— фиктивное удлинение корпуса;
— удлинение корпуса;
Коэффициент центра давления относительно теоретической вершины корпуса
при =0,3:
;
Коэффициент лобового сопротивления корпуса
при =0,3:
;
Коэффициент подъёмной силы корпуса
при =0,3:
;
Аэродинамическое качество корпуса
при =0,3:
Моментные характеристики корпуса
Координата центра давления корпуса
при =0,3:
м;
Коэффициент аэродинамического давления корпуса
при =0,3:
;
Коэффициент запаса статической устойчивости
при =0,3:
;
Коэффициент аэродинамического момента относительно центра тяжести
при =0,3:
;
Производная коэффициента аэродинамического момента по углу атаки α
при =0,3:
;
Производная коэффициента аэродинамического момента относительно центра тяжести по углу атаки α
при =0,3:
;
Таблица 3
|
Число Маха |
||||||
|
=0,3 |
0.016 |
0.289 |
0.034 |
0.035 |
0.014 |
0.409 |
|
Число Маха |
||||||
|
=0,3 |
0.256 |
-0.0041 |
-0.267 |
0.00427 |
-0.075 |
0.077 |
Расчёт аэродинамических коэффициентов ЛА (конус + цилиндр + оперение)
Коэффициент и абсолютное значение нормальной силы ЛА
при =0,3:
;
H;
Производная коэффициента нормальной силы ЛА по углы атаки
=0,3:
;
Коэффициент и абсолютное значение продольной силы ЛА
при =0,3:
;
Н;
Коэффициент и абсолютное значение лобового сопротивления ЛА
при =0,3:
;
H;
Коэффициент и абсолютное значение подъёмной силы ЛА
при =0,3:
;
H;
Аэродинамическое качество ЛА
при =0,3:
;
Моментные характеристики ЛА:
Координата центра давления ЛА
при =0,3:
м;
Коэффициент центра давления
при =0,3:
;
Коэффициент аэродинамического момента
при =0,3:
;
Коэффициент запаса статической устойчивости
при =0,3:
;
Производная коэффициента аэродинамического момента относительно центра тяжести
при =0,3:
;
Производная коэффициента аэродинамического момента по углу атаки α
при =0,3:
;
Производная коэффициента аэродинамического момента относительно центра тяжести по углу атаки α
при =0,3:
;
Таблица 4
|
Число Маха |
||||||
|
=0,3: |
0.031 |
0.582 |
0.038 |
0.039 |
0.029 |
0.743 |
|
Число Маха |
||||||
|
=0,3: |
0.613 |
-0.019 |
0.089 |
-0.00277 |
-0.357 |
-0.052 |
Расчёт аэродинамических коэффициентов ЛА (конус + цилиндр + оперение + крыло)
Коэффициент и абсолютное значение нормальной силы ЛА
при =0,3:
;
H;
Производная коэффициента нормальной силы ЛА по углы атаки
=0,3:
;
Коэффициент и абсолютное значение продольной силы ЛА
при =0,3:
;
Н;
Коэффициент и абсолютное значение лобового сопротивления ЛА
при =0,3:
;
H;
Коэффициент и абсолютное значение подъёмной силы ЛА
при =0,3:
;
H;
Аэродинамическое качество ЛА
при =0,3:
;
Моментные характеристики ЛА:
Координата центра давления ЛА
при =0,3:
м;
Коэффициент центра давления
при =0,3:
;
Коэффициент аэродинамического момента
при =0,3:
;
Коэффициент запаса статической устойчивости
при =0,3:
;
Коэффициент аэродинамического момента относительно центра тяжести
при =0,3:
;
Производная коэффициента аэродинамического момента по углу атаки α
при =0,3:
;
Производная коэффициента аэродинамического момента относительно центра тяжести по углу атаки α
при =0,3:
;
Таблица 5
|
Число Маха |
||||||
|
=0,3: |
0.135 |
2.575 |
0.05 |
0.057 |
0.132 |
2.312 |
|
Число Маха |
||||||
|
=0,3: |
0.565 |
-0.076 |
0.04 |
-0.00545 |
-1.455 |
-0.104 |
Схемы расположения точек приложения нормальной силы на ЛА.
Скачать: kursovaya_rabota-1.docx


 ис.
ис.