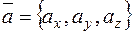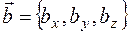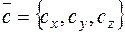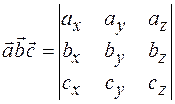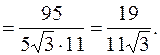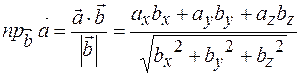Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Вычисление площади треугольника построенного на векторах.
Этот калькулятор онлайн вычисляет площадь треугольника построенного на векторах. Треугольник может быть задан координатами двух векторов или координатами трех вершин треугольника.
Онлайн калькулятор для вычисления площади треугольника построенного на векторах не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac<2> <3>)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac<5> <7>)
http://ru.onlinemschool.com/math/assistance/vector/triangle_area/
http://www.math-solution.ru/math-task/vect-area-triangle
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Онлайн калькулятор. Площадь треугольника построенного на векторах.Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденый материал. Калькулятор для вычисления площади треугольника построенного на векторахВыберите каким образом задается треугольник: Введите значения векторов: Введите координаты точек: Инструкция использования калькулятора для вычисления площади треугольника построенного на векторахВвод данных в калькулятор для вычисления площади треугольника построенного на векторахВ онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах
Теория. Площадь треугольника построенного на векторахОпределение Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов: Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Решение задач по математике онлайн |
Геометрия 10-11 класс
50 баллов
Даны координаты вершин пирамиды ABCD :
A(5;−1;− 4), B(9;3;− 6), C(7;10;−14), D(5;1;− 3).
Необходимо:
1. Записать векторы_____
AB,
_____
AC ,
_____
AD в ортонормальной системе {i j k} , ,
и найти модули этих векторов.
2. Найти угол между векторами AB и AC .
3. Найти проекцию вектора AD на вектор AB.
4. Вычислить площадь грани ABC .
5. Найти объем пирамиды ABCD .
Ирина Каминкова
18.11.2020 16:44:34
Ответ эксперта
Ирина Каминкова
18.11.2020 16:45:04
Ответ эксперта
Все предметы
Рейтинг пользователей
Добрый день люди добрые! 
Даны координаты: A (4, 2, 5), B (0, 7, 2), C (0, 2, 7)
Площадь ABC = длине векторов AB * AC
По моим подсчетам:
вектор AB имеет координаты= (-4, 5, -3)
вектор AC имеет координаты = (-4, 0, 2)
Теперь вычисляем 3 координату, умножив AB на AC, у меня получилось 3 координата = (10, -7, 9)
Теперь найдем длину векторного произведения и вычислим площадь.
Вот у меня в конечном итоге получился ответ корень из 230, но площадь же не может быть корнем.
Помогите мне пожалуйста, перерешайте, если не правильно…
|
|
 |
|
||||
| Теги: векторы в пространстве, метод координат, сумма векторов, скалярное произведение векторов |
Все ответы
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
Векторная алгебра.
1. Демонстрационный пример решения контрольной работы.
Даны координаты вершины пирамиды АВСD:
А(5; -3;1), В(0;2;6), С(-1; 4;7), D( 3;-6;5).
Требуется:
1) записать векторы в системе орт и найти модули этих векторов;
2) найти угол между векторами и ;
3) найти проекцию вектора на вектор ;
4) найти площадь грани ABC;
5) найти объем пирамиды ABCD.
Решение:
1) Запись вектора в системе орт имеет вид 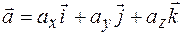
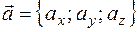
Длина или модуль вектора находится по формуле 
Найдем координаты вектора 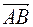
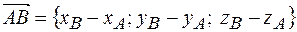
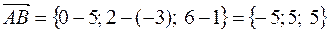
или в системе орт 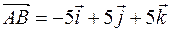
Модуль вектора 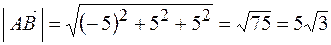
Аналогично, координаты вектора 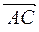
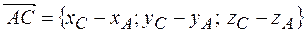
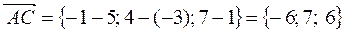
или в системе орт 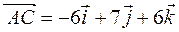
Модуль вектора 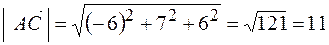
Найдем координаты вектора 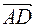

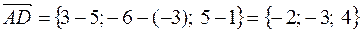
или в системе орт 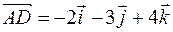
Модуль вектора 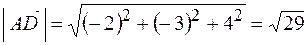
2)Определение. Скалярным произведением 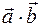
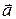
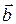
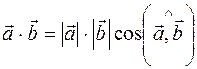
Теорема.Скалярное произведение векторов 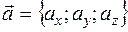
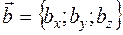
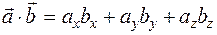
Скалярное произведение позволяет находить угол между векторами, координаты которых известны. Из определения скалярного произведения имеем:
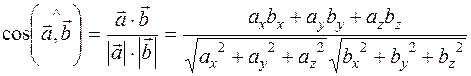
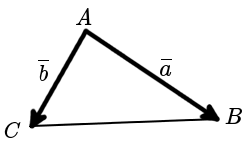
Найдем угол между векторами 
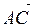


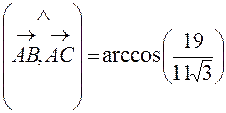
3) Скалярное произведение позволяет находить проекцию вектора на вектор
Найдем проекцию вектора 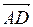


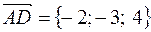
4) Определение. Векторным произведением 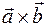
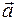
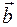
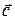
1) 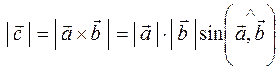
2) 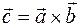
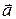
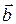
3) 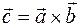
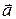
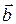
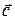
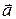
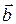
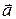
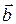
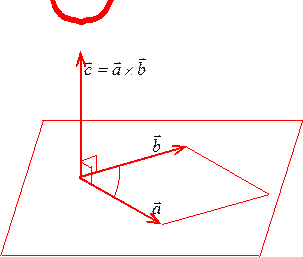
Геометрический смысл векторного произведения. Модуль векторного произведения 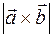
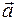
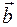
Теорема. Векторное произведение векторов 
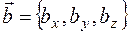
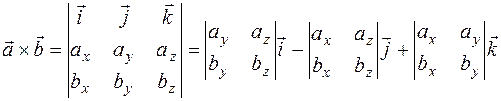
Найдем площадь грани ABC, как треугольника, построенного на векторах

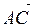
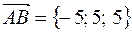
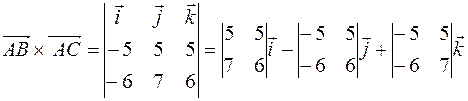
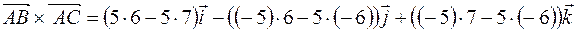
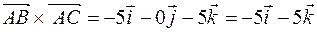
Модуль 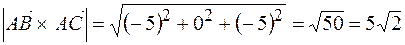
Площадь треугольника ABC равна 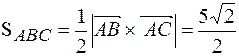
5) Смешанное произведение 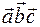
Теорема. Пусть