Как найти площадь боковой поверхности конуса получившегося - Avtoru.top

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.

Формула вычисления площади конуса
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
Примеры задач

Формула вычисления площади конуса

1. Боковая поверхность

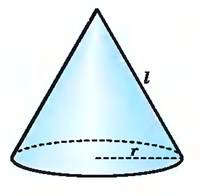
Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.

S_бок. = πRl

Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности.

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

Основанием конуса является круг, площадь которого вычисляется так:

S_осн. = πR²

Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:

S_осн. = π(d/2)²

3. Полная площадь

Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:

S_полн. = πRl + πR² = πR(l + R)

Примеры задач

Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.

Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см².

Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l² = (4 см)² + (3 см)² = 25 см².
l = 5 см.

Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см².

Источник

Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R. Соединим произвольную точку A этого круга с точкой S отрезком AS. Если точка А будет описывать круг с радиусом R, то отрезки AS будут заполнять некоторое тело. Это тело называют круговым конусом.

Границей конуса является круг радиуса R и боковая поверхность конуса.
Боковую поверхность описывает отрезок AS , когда точка A описывает круг.
Точка S является вершиной конуса. Множество отрезков AS, соединяющих вершину с окружностью основания являются направляющими конуса.Если перпендикуляр, опущенный из точки S, совпадает с центром основания, то конус называется прямым.Очень часто говорят, что прямой конус образуется в результате вращения прямоугольного треугольника вокруг оси, содержащий его катет.
На данном рисунке прямой конус получился в результате вращения прямоугольного треугольника AOS вокруг катета SO. Тогда говорят, что

Катет SO –это высота конуса;
Гипотенуза AS –образующая конуса;
Катет AO – радиус конуса.

Площадь боковой поверхности конуса через его радиус и направляющую

Пусть дан конус с радиусом R и образующей L
AS=L, AO=R

Разрежем конус по образующей L и развернем его боковую поверхность.
В результате получим криволинейный треугольник ASA` , где AS=L, A`S=L.
Дуга AA` -это вытянутая окружность основания конуса с радиусом R. Следовательно, длина дуги AA` будет равна 2πR
Площадь боковой поверхности будет равна площади сектора круга с радиусом R.
Если угол α – радиальная мера угла, то: $S=L^2 {{alpha}/2}={AS}{{alpha}/2}$
где α=∠{ASA`}
Чтобы найти угол ∠{ASA`} воспользуемся формулой длины дуги, которая стягивает данный угол:
Но с другой стороны:
Приравняем правые части равенств. Имеем:
Выразим α:
Подставим полученное выражение в формулу площади сектора: $S=L^2*{{alpha}/2}=L^2*{{2{pi}R}/{2L}}={pi}RL$
Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.
Формула боковой поверхности конуса будет иметь следующий вид:

Пример расчета площади боковой поверхности конуса, если известны его радиус и направляющая
Найти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 см
По условию задачи L = 5см, R=3см
Формула боковой поверхности конуса:

Подставив в формулу значения из условия задачи, имеем:

Площадь боковой поверхности конуса через его радиус и высоту

Очень часто в задачах на вычисление площади боковой поверхности конуса известна высота конуса вместо его направляющей.
Так как конус прямой, то треугольник AOS – прямоугольный, где AO и OS – катеты, а AS –гипотенуза. Воспользовавшись теоремой Пифагора, получаем: ${AS}^2={AO}^2+{OS}^2$
Отсюда: $AS=sqrt{{AO}^2+{OS}^2}$
Но
Тогда: $L=sqrt{R^2+H^2}$
Подставим данное выражение в формулу площади боковой поверхности конуса: $S={pi}R sqrt{R^2+H^2}$
Боковая поверхность конуса равна произведению числа на радиус конуса и корень квадратный из суммы квадратов радиуса и высоты конуса

Пример расчета площади боковой поверхности конуса, если известны его радиус и высота.
Найти площадь боковой поверхности конуса с радиусом равным 1 см и высотой, равной 5 см
По условию задачи Н = 5см, R=1см
Формула боковой поверхности конуса:
$S={pi}R sqrt{R^2+H^2}$
Подставив в формулу значения из условия задачи, имеем:
$S={pi}*1*sqrt{1^2+5^2}={pi} sqrt{25}=5{pi}$

Полная поверхность конуса

Полная поверхность конуса – это сумма площади его боковой поверхности и площади основания конуса:

Основанием конуса является круг с радиусом R. Его площадь равна произведению числа π на квадрат его радиуса: $S_osn={pi}R^2$
Площадь боковой поверхности вычисляется по формуле: $S_bok={pi}RL$ или $S_bok={pi}R sqrt{R^2+H^2}$
Тогда площадь полной поверхности конуса равна: $S_poln={pi}RL+{pi}R^2={pi}R(L+R)$
или $S_poln={pi}Rsqrt{R^2+H^2}+{pi} R^2={pi}R(sqrt{R^2+H^2}+R)$
Таким образом, площадь полной поверхности конуса равна произведению числа {pi} на радиус конуса и сумму направляющей и радиуса.
Формула имеет следующий вид: $S_poln={pi}R(L+R)$
Площадь полной поверхности конуса равна произведению числа π на радиус конуса и сумму корня квадратного из суммы квадратов радиуса и высоты конуса и радиуса конуса.
Формула имеет следующий вид: $S_poln={pi}R(sqrt{R^2+H^2}+R)$

Источник

Как рассчитать площадь поверхности конуса

На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.

Конус — геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

Образующая конуса — это отрезок, соединяющий вершину и границу основания.

Боковая поверхность через радиус и образующую

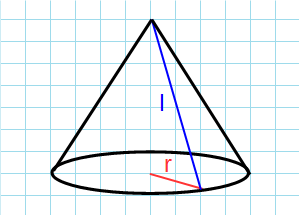
Формула боковой поверхности конуса через радиус и образующую:

π — константа равная (3.14); l — образующая конуса; r — радиус основания конуса.

Боковая поверхность через радиус и высоту

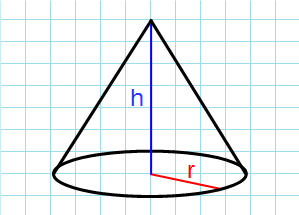
Формула боковой поверхности конуса через радиус и высоту:

π — константа равная (3.14); h — высота конуса; r — радиус основания конуса.

Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:

π — константа равная (3.14); l — образующая конуса; r — радиус основания конуса.

Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:

π — константа равная (3.14); h — высота конуса; r — радиус основания конуса.

Источник

На этом уроке мы выведем и научимся применять
формулы для вычисления площади боковой поверхности конуса и площади полной
поверхности конуса.

Для начала давайте вспомним, что же это за
геометрическое тело – конус.

Итак, тело, ограниченное
конической поверхностью и кругом с границей , называется конусом.

Напомним, что боковой поверхностью конуса
называется фигура, образованная всеми образующими конуса.

На экране изображён конус, у которого радиус
равен , а
образующая равна . Боковую
поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на
плоскость, разрезав её по одной из образующих.

Давайте представим, что боковую поверхность
конуса разрезали по образующей и развернули
таким образом, что получился круговой сектор .

Стороны и которого
являются двумя краями разреза боковой поверхности конуса.

Развёрткой боковой поверхности
конуса является круговой сектор. Обратите внимание, радиус сектора равен
образующей конуса, т.е. .
А длина дуги сектора равна длине окружности основания конуса, т.е. равна .

За площадь боковой поверхности конуса
принимается площадь её развёртки. Выразим площадь боковой поверхности конуса
через его образующую и радиус
основания .

Площадь кругового сектора – развёртки боковой
поверхности конуса – равна , где – градусная
мера дуги .

Выразим через длину
дуги и радиус окружности. Длина дуги окружности с градусной мерой и радиусом равна . С другой
стороны, длина этой дуги равна два пи эр, т.е. пи эль альфа деленное на сто
восемьдесят равно . Отсюда, . Подставим
это выражение в формулу площади боковой поверхности конуса. Тогда площадь
боковой поверхности конуса равна . Т.е.
площадь боковой поверхности конуса с образующей и радиусом
основания выражается следующей
формулой: .

Таким образом, площадь боковой поверхности
конуса равна произведению половины длины окружности основания на образующую.

Теперь выведем формулу для вычисления площади
полной поверхности конуса.

Вообще, площадью полной поверхности
конуса называется сумма площадей боковой поверхности и основания. Формулу
для вычисления площади боковой поверхности конуса мы с вами выразили выше, а площадь круга равна . Подставим
все данные в формулу.

Упростим. Отсюда, получаем, что площадь полной
поверхности конуса равна .

А сейчас давайте решим несколько задач на
применение выведенных формул.

Задача: образующая конуса равна
см, а его
высота – см.
Вычислите площадь боковой поверхности конуса.

Решение: запишем формулу для
вычисления площади боковой поверхности конуса.

Теперь внимательно рассмотрим рисунок.

Напомним, что высота конуса перпендикулярна
его основанию. А, значит, она перпендикулярна любой прямой, лежащей в плоскости
основания конуса. Следовательно, высота конуса .

Рассмотрим . Он
прямоугольный. Применяя теорему Пифагора, найдём длину стороны , которая и
является радиусом основания конуса. Получаем, что ОА равно .

Подставим длину образующей конуса и его радиус
в формулу для вычисления площади боковой поверхности конуса. Посчитаем.
Получим, что площадь боковой поверхности конуса равна .

Запишем ответ.

Задача: радиус основания конуса
равен дм, а
площадь его осевого сечения – дм².
Вычислите площадь боковой поверхности конуса.

Решение: запишем формулу для
вычисления площади боковой поверхности конуса.

Теперь рассмотрим рисунок.

Напомним, что осевым сечением конуса называется сечение
конуса плоскостью, проходящей через его ось, и представляет собой равнобедренный треугольник, основание которого –
диаметр основания конуса, а боковые стороны – образующие конуса. Значит, – равнобедренный.

Так как по
условию задачи радиус основания конуса равен 9 дм, то основание осевого сечения
равно .

Напомним, что
площадь треугольника равна половине произведения длины основания на высоту . Выразим из формулы высоту . Получаем, что высота треугольника, а она является и
высотой конуса, равна .

Рассмотрим . Он прямоугольный, так как . Применяя теорему Пифагора, найдём длину . Получаем, что . Обратите внимание, гипотенуза есть образующая нашего конуса.

Подставим
найденную длину образующей конуса и его радиус в формулу для вычисления площади
боковой поверхности конуса. Посчитаем. Получим, что площадь боковой поверхности
конуса равна .

Не забудем
записать ответ.

Задача: прямоугольный треугольник, длины катетов которого
равны см и см, вращается вокруг меньшего катета. Вычислите
площадь полной поверхности конуса, образованного при этом вращении.

Решение: запишем формулу для вычисления площади полной
поверхности конуса.

Рассмотрим . Он прямоугольный по условию.

Воспользуемся теоремой
Пифагора и найдём длину гипотенузы , которая и является образующей конуса. Имеем, .

Так как по
условию задачи треугольник вращается вокруг меньшего катета, то радиус
основания конуса, образованного при этом вращении, равен .

Подставим длину
образующей конуса и его радиус в формулу для вычисления площади полной
поверхности конуса. Посчитаем. Получим, что площадь полной поверхности нашего
конуса равна .

Запишем ответ.

Итоги:

На этом уроке
мы вывели формулы для вычисления площади боковой поверхности конуса и
площади полной поверхности конуса. А также научились их применять при решении
задач.

Источник

Теорема: Площадь боковой поверхности конуса равна произведению полуокружности его основания и образующей.

Доказательство.

Пусть имеется конус, радиус основания которого равен r, а образующая I (рисунок).

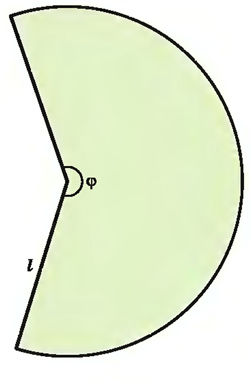
Развернем боковую поверхность конуса на плоскость, в результате получится сектор, радиус которого равен образующей I (рисунок ниже).

Найдем центральный угол ϕ этого сектора, приняв во внимание, что ему соответствует дуга окружности, равная длине окружности основания конуса, т. е. равна 2πr. Поскольку длина всей окружности, связанной с сектором, равна 2πl и этой длине соответствует полный угол, равный 360°, то

Теперь найдем площадь S сектора с радиусом I и углом ср:

Поскольку выражение πr представляет длину полуокружности основания конуса, можем утверждать, что площадь боковой поверхности конуса равна произведению полуокружности его основания и образующей.

Источник

Формула вычисления площади конуса

1. Боковая поверхность

2. Основание

3. Полная площадь

Примеры задач

Площадь боковой поверхности конуса через его радиус и направляющую

Площадь боковой поверхности конуса через его радиус и высоту

Полная поверхность конуса

Как рассчитать площадь поверхности конуса

Боковая поверхность через радиус и образующую

Боковая поверхность через радиус и высоту

Полная площадь через радиус и образующую

Полная площадь через радиус и высоту

Не пропустите также: