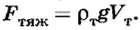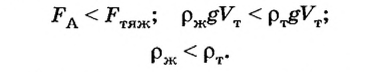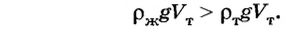§ 1 Расчет архимедовой силы, условие плавания тел: формулы и определения
Рассмотрим решение задач на расчет архимедовой силы, условие плавания тел в жидкостях и газах.
Для решения задач нам нужно вспомнить следующие формулы и определения:
Архимедова силаравна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.
Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе: P выт.жидкости = P тела.
Морские и речные суда могут перевозить грузы. Вес груза зависит от водоизмещения судна. Водоизмещение — это вес воды, вытесненной судном, равный его весу в воздухе.
Подъемная сила аэростатовравна разности между архимедовой силы и весом оболочки, гондолы и газа, которым наполнен аэростат.
При решении задач важно верно выразить величины в системе СИ.
Архимедова сила зависит от объема тела, поэтому вспомним размерности объема:
1 дм3 = 0,001 м3;
1 см3 = 0, 000 001 м3.
§ 2 Решение задач
Задача 1:Вычислите архимедову силу, действующую на брусок размером 2х10х4 см, если он наполовину погружен в спирт.
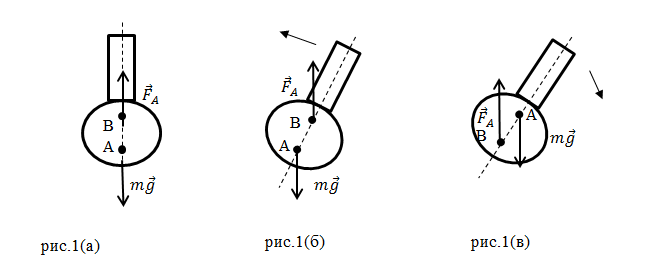
Решение:Запишем условие задачи. Нам известны размеры бруска: длина а = 10 см, ширина b=2 см, высота c=4 см. Плотность спирта ρж = 800 кг/м3. Выразим длину, ширину и высоту в системе СИ: 0,1 м, 0,02 м, 0,04 м.
Для решения запишем формулу вычисления архимедовой силы: Fa = gρжVпогр.части тела.
Объем всего бруска прямоугольной формы равен произведению длины на ширину и на высоту: V=abc = 0,1 м*0,02*0,04 м = 0,00 008 м3.
Объем погруженной части равен половине объема: Vпогр.части тела=0,00 004 м3.
Подставим числовые значения плотности спирта, коэффициента силы тяжести, объема погруженной части тела в формулу архимедовой силы и получим: Fa = 0,32 Н.
Ответ: на брусок в спирте действует архимедова сила 0,32 Н.
Задача 2:Какую силу нужно приложить к плите массой 4 т при ее подъеме со дна водоема, если объем плиты — 2 м3?
Решение:запишем условие задачи. Масса плиты m = 4 т, выразим в СИ: 4000 кг, объем плиты V = 2 м3, плотность воды ρж = 1000 кг/м3.
На тело, погруженное в жидкость или газ, действуют две силы: сила тяжести и архимедова сила, направленные противоположно. Поэтому вес плиты в воде уменьшается: Pв воде = Pв воздухе – Fа .
Вес тела в воздухе найдем по формуле P=mg, архимедову силу определим по формуле Fa = gρжVпогр. тела.
Тогда формула веса плиты в воде запишется так: Pв воде = mg — gρжVпогр. тела.
Подставим числовые значения величин, произведем вычисления и получим ответ: вес плиты в воде равен 20 000 Н, следовательно, для поднятия плиты в воде нужно приложить силу 20 кН.
Ответ: для поднятия плиты в воде нужно приложить силу 20 кН.
Задача 3: Какой по весу груз может удержать на поверхности воды пробковый пояс объемом 6,25 дм3 и массой 2 кг, если пояс будет погружен в воду полностью?
Решение: Запишем условие задачи. Нам известны объем пояса V = 6,25 дм3, его масса m = 2 кг, плотность воды ρж = 1000 кг/м3. Выразим объем в СИ, для этого 6, 25 поделим на 1000, равно 0,00 625 м3. Найти вес груза Pгр.
Известно, что вес груза, перевозимого судами, равен разности между водоизмещением судна и его весом. Водоизмещение — это вес воды, вытесненной судном с грузом. Тогда Pгруза = Pвытесненной воды — Pсудна.
Пробковый пояс при полном погружении вытесняет воду в объеме, равном объему пояса. Вычитая из веса вытесненной воды собственный вес пояса, можем найти вес груза:
Pгруза = Pвыт.воды – Pпояса.
Определим вес вытесненной воды. Для этого массу вытесненной воды умножим на коэффициент силы тяжести, а масса воды равна произведению плотности воды на ее объем. Объем вытесненной воды равен объему спасательного пояса. Тогда вес вытесненной воды равен произведению плотности воды на объем пояса и коэффициент тяжести:
Pвыт.воды = ρводы *Vводы *g
Определим вес пояса по формуле Pпояса =mпояса·g.
Подставим числовые значения величин и вычислим вес вытесненной поясом воды и вес пояса. Тогда вес груза равен их разности.
Ответ: пробковый пояс может удерживать в воде груз весом 42,5 Н.
Задача 4:Аэростат объемом 2000 м3 наполнен водородом. Вес оболочки и гондолы 16 000 Н. Определите подъемную силу аэростата.
Решение: Запишем условие задачи. Известны объем аэростата V = 2000 м3, вес оболочки и гондолы вместе Pоб =16 000 Н, плотность водорода, которым наполнен аэростат, ρгаза = 0,09 кг/м3, плотность воздуха при нормальном атмосферном давлении ρвозд. = 1,29 кг/м3. Все данные приведены в системе СИ. Требуется найти подъемную силу Fподъемн.
На аэростат действуют сила тяжести и архимедова сила, которая поднимает его вверх. Сила тяжести действует на оболочку, гондолу и газ, которым он наполнен. Вес оболочки и гондолы известен, нужно найти вес водорода, для этого массу водорода умножим на коэффициент тяжести. Массу водорода найдем по формуле плотности. Тогда вес газа равен произведению плотности газа на объем аэростата и коэффициент тяжести: Pгаза = ρгаза *Vаэростата *g.
Архимедову силу определим по формуле Fa = gρжVаэростата.
Подставим записанные формулы в формулу подъемной силы, вынесем одинаковые множители за скобки, вычислим.
Ответ: подъемная сила аэростата равна 8000 Н = 8 кН.
§ 3 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
При решении задач нужно помнить основные формулы и определения.
Архимедова сила равна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.
Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе.
Водоизмещение — это вес воды, вытесненной судном с грузом, равный весу судна вместе с грузом. Вес груза, перевозимого судами или выдерживаемого спасательным поясом, плотом, льдиной, равен разности между весом вытесненной жидкости и весом самого судна, пояса, плота, льдины.
Подъемная сила аэростатов равна разности между архимедовой силы и весом аэростата (т.е. весом оболочки, гондолы и газа, которым наполнен аэростат).
Плавание тел в физике, теория и онлайн калькуляторы
Плавание тел
Сила Архимеда
Если тело находится в жидкости или газе, но на него действует выталкивающая сила, называемая силой Архимеда. Она возникает как результат того, что давление в жидкости (газе) увеличивается с погружением в глубину вещества. При этом сила гидростатического давления на тело в жидкости (газе) сверху вниз меньше, силы давления, направленной снизу вверх.
Определение
Сила Архимеда ($F_A)$ равна весу жидкости (газа) в объеме тела, находящегося в ней:
[F_A=rho Vg left(1right),]
где $rho $ — плотность жидкости (газа); $V$ — объем тела, находящийся в веществе; $g$ — ускорение свободного падения.
Сила Архимеда появляется только тогда, когда на жидкость (газ) действует сила тяжести. Так, в невесомости гидростатическое давление равно нулю соответственно, нет силы Архимеда.
И так, если тело погружено в жидкость, при этом оно находится в состоянии механического равновесия, то со стороны окружающей жидкости на тело действует выталкивающая сила (сила Архимеда). Данная сила направлена вверх. Она проходит через центр масс жидкости, вытесненной телом (обозначим эту точку буквой А). Точку А называют центром плавучести тела. Положением точки плавучести определяют равновесие и устойчивость плавающего тела.
Условия плавания тел
Закон Архимеда дает разъяснение всех вопросов, связанных с плаванием тел. Допустим, что тело находится в жидкости и оно предоставлено самому себе. Если вес тела больше, чем вес жидкости, которую оно вытесняет, то тело тонет. Если вес тела равен весу вытесненной им жидкости, то тело находится в равновесии внутри этой жидкости в любой ее точке. Если вес тела меньше, чем вес вытесненной им жидкости, то тело всплывает, двигаясь к поверхности жидкости. Достигнув поверхности, тело плавает так, что его часть выступает над поверхностью жидкости. Плавающие тела, обладающие разными плотностями, имеют над поверхностью жидкости разные доли своего объема.
Если тело, находящееся в жидкости, однородно ( то есть его плотность ($rho =const$) постоянна), то условия плавания тел в жидкости (${rho }_g-$плотность жидкости) формулируют так$:$
- При $rho >{rho }_g$, тело тонет;
- При $rho <{rho }_g$ тело всплывает;
- При $rho ={rho }_g$ тело плавает (находится в равновесии) в жидкости.
Если тело неоднородно, то формулируя условия плавания тела сравнивают его среднюю плотность и плотность жидкости.
В том случае, если тело плавает на границе нескольких жидкостей с разными плотностями, то сила Архимеда равна:
[F_A=left({rho }_1V_1+{rho }_2V_2+dots {rho }_NV_Nright)gleft(2right),]
${rho }_1$ — плотность первой жидкости; ${rho }_2$ — плотность второй жидкости; $V_1$ — объем части тела, находящийся в первой жидкости; $V_2$ — объем этого же тела, находящийся во второй жидкости …
Равновесие тел в жидкости
Закон Архимеда позволяет решать вопрос, связанный с равновесием тел в жидкости. Для равновесия необходимо, чтобы вес тела равнялся весу вытесненной им жидкости, при этом центр плавучести А должен находиться на одной вертикали с центром масс самого тела. При определении устойчивости равновесия выделяют два случая.
- Плавающее тело полностью находится в жидкости. В этом случае при всяких поворотах и смещениях центр масс тела и центр плавучести сохраняют свое положение по отношению к телу. Равновесие будет устойчивым, если центр масс тела находится ниже центра плавучести.
- Плавающее тело погружено в жидкость частично. Его часть выступает над свободной поверхностью жидкости.
При смещении тела из положения равновесия в этом случае изменяется форма вытесняемого телом объема жидкости. Положение
центра плавучести относительно тела изменяется. В этом случае вводится понятие метацентра плавающего тела.
Это точка, назовем ее М, которая получается при пересечении вертикальной оси симметрии тела и линии действия
выталкивающей силы. Если метацентр ниже центра масс тела, то положение равновесия не устойчиво.
Примеры задач на плавание тел
Пример 1
Задание: Тело плавает на поверхности вещества, плотность которого равна ${rho }_1$, при этом объем погруженной части тела составляет $n $- ую часть от всего объема тела. Какая часть объема тела при его плавании будет
погружена в жидкость, плотность которой составит ${rho }_2?$ Тело считать однородным.
Решение: Для того чтобы тело плавало в жидкости вес этого тела должен быть равен весу жидкости объем которой равен объему тела, находящейся в ней, поэтому для первой жидкости запишем, что:
[mg={rho }_1nVg left(1.1right),]
где $m=rho Vg$- масса плавающего тела; $rho $ — плотность тела.textit{}
Выразим плотность тела, используя выражение (1.1):
[rho =n{rho }_1left(1.2right).]
Условием плавания тела того же тела во второй жидкости станет:
[n{rho }_1Vg={rho }_2V_xg left(1.3right),]
где $V_x$ — объем тела погруженный во вторую жидкость. Найдем отношение $frac{V_x}{V}$ из формулы (1.3):
[frac{V_x}{V}=frac{n{rho }_1}{{rho }_2}.]
Ответ: Погруженная часть составит $frac{V_x}{V}=frac{n{rho }_1}{{rho }_2}$
Пример 2
Задание: Тело полностью погружено в жидкость и плавает в ней. Объясните, почему равновесие будет устойчивым, если центр масс тела находится ниже центра его плавучести.
Решение: При нормальном положении центр тяжести и центр плавучести находятся на одной вертикальной прямой (рис.1 (а)). Центр плавучести (А) выше центра тяжести (B). Тело находится в равновесии. Тело наклоняется (рис.1(б)), при этом сила тяжести и сила Архимеда образуют пару сил, которая возвращает тело в исходное положение. Если центр плавучести будет находиться ниже центра тяжести, при отклонении от вертикального положения сила тяжести и сила выталкивания образуют пару сил, которая поворачивает тело дальше от положения равновесия (рис.1(в)).
Если центр тяжести совпадает с центром плавучести, то равновесие называют безразличным. В этом случае центр плавучести играет роль точки повеса.
Читать дальше: плоская волна.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание:
Условия плавания тел:
Вы уже знаете, что на погружённое в жидкость тело действуют две силы: сила тяжести
Под действием этих сил тело будет двигаться в сторону большей силы. При этом возможные следующие случаи:
- Если сила тяжести меньше архимедовой силы
то тело будет всплывать (рис. 144, а). На поверхности оно будет плавать, частично погрузившись на глубину, которой достаточно для возникновения архимедовой силы, уравновешивающей вес тела.
- Если сила тяжести равна архимедовой силе
, то тело будет находится в равновесии в любом месте жидкости (рис. 144 ,б).
- Если сила тяжести больше архимедовой силы
то тело утонет (рис. 144, в).
Рассмотренные условия плавания тел в каждом случае определяются соотношением между плотностями жидкости и погружённого тела.
- Если плотность тела меньше плотности жидкости
, то тело будет плавать на поверхности, частично погрузившись в воду.
- Если плотность тела равна плотности жидкости , то будет наблюдаться состояние безразличного (индифферентного) равновесия, когда тело может зависнуть на любой глубине (в водоёмах это представляет опасность для судоходства из-за возможного столкновения).
- Если плотность тела больше, чем плотность жидкости
, то тело будет тонуть.
Подводная лодка, опустившись на илистое дно, иногда с трудом может оторваться от него. Такое присасывание лодки ко дну возникает в том случае, когда лодка прижимается к грунту так, что между нею и грунтом нет воды. Значит, вода не давит на его нижнюю часть, т. е. не возникает выталкивающей силы.
Для выполнения подводных работ используют водолазные костюмы (рис. 145).
Они имеют массу до и более 50 кг, так как подошвы в них делают свинцовыми, чтобы увеличить вес водолаза и придать ему большую устойчивость во время — работы в воде. Как же может водолаз передвигаться в таком тяжёлом костюме? Благодаря значительному объёму костюма выталкивающая сила воды уравновешивает почти ведь его вес, поэтому водолаз может свободно передвигаться в воде.
Пользуясь аквалангом, изобретённым известным исследователем морских глубин французским учёным Жаком-Ивом Кусто, человек может долго находиться в воде и свободно плавать (рис. 146).
Для исследования морей и океанов на больших глубинах используют батисферы и батискафы. Батисфера (от греческих слов батис — глубокий и сфера) — это очень прочный стальной шар с иллюминаторами (окнами) из толстого стекла. Внутри шара находятся исследователи, поддерживающие связь с кораблём. Батисферу опускают на стальном тросе.
Батискаф (от греческих слов батис — глубокий; скафос — судно) отличается от батисферы тем, что он не удерживается на тросе, а имеет собственный двигатель и может свободно перемещаться на больших глубинах (до 11 км) в любых направлениях (рис. 147).
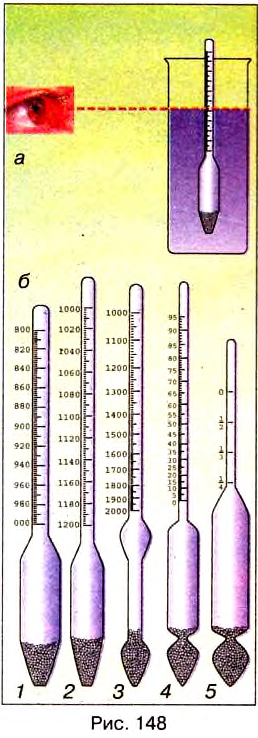
Тело, имеющее меньшую плотность, чем некоторые жидкости, по-разному погружается в них. Это явление используют в ареометрах (от греческих слов араиос — жидкий и метрео — измеряю) — приборах для измерения плотности жидкости по глубине их погружения. Любой ареометр — это стеклянный поплавок в виде трубки с делениями и грузом внизу (рис. 148, а). Он погружается в жидкость тем глубже, чем меньше плотность жидкости. В нижней части ареометра может быть термометр для измерения температуры исследуемой жидкости.
Ареометры имеют ещё и другое название; их називають денсиметрами (от латинских слов денсус — густой и метрео). Денсиметрами можно измерять плотности жидкостей от 0,7 до 2,0 На рисунке 148, б изображены денсиметры разных видов:
Плавающее тело своей подводной частью вытесняет воду. Вес этой воды равней силе тяжести, действующей на это тело. Это справедливо и для любого судна. Вес воды, которую вытесняет подводная часть судна, равен силе тяжести, действующей на судно с грузом.
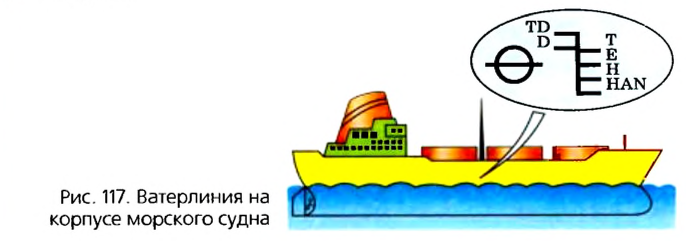
Все суда погружаются в воду на определённую глубину, называемую осадкой. Максимально допустимую осадку обозначают на корпусе судна красной линией, называемую ватерлинией (от голландского слова ватер — вода). Кроме ватерлинии на судах делают и другие пометки, обозначающие уровни погружения судна в разных морях и океанах в зависимости от времени года (рис. 149).
Это связано с тем, что плотность воды в различных местах Мирового океана разная, кроме того, она ещё зависит и от температуры воды (летом плотность меньше, чем зимой).
Каждое судно имеет свое водоизмещение. Водоизмещение судна — это вес вытесненной судном воды, равный силе тяжести, действующей на судно с грузом при его погружении в воду.
Наибольшие суда используют для перевозки нефти, их называют танкерами. Водоизмещение таких судов достигает 5 ООО ООО ООО Н.
Свыше 200 лет отделяют нас от первых воздушных полётов человека. 5 мая 1783 г. — первая публичная демонстрация полёта оболочки, наполненной горячим воздухом. 21 ноября того же года французские изобретатели братья Жозеф и Этьенн Монгольфье осуществили первый полёт воздухоплавателей (рис. 150).
А через 10 дней французский физик Жак Шарль отправился в путешествие по воздушному океану на аэростате собственной конструкции, оболочка которого была наполнена водородом. Этот аэростат стал прообразом дирижаблей.
Для исследования верхних слоёв атмосферы на метеорологических станциях запускают небольшие, диаметром 1—2 м, воздушные шары-зонды (рис. 151). Они поднимаются на высоту до 35—40 км. К ним подвешивают приборы, посылающие по радио сигналы о высоте полёта, давлении, температуре воздуха. По направлению и скорости полёта шара можно определить направление и силу ветра на разных высотах. Сведения, получаемые с таких зондов, очень важны для прогнозирования погоды.
На рисунке 152 изображён управляемый летательный аппарат, который легче воздуха — дирижабль.
Этот аппарат приводят в движение винты, которые вращаются двигателями. Существенный недостаток аппаратов такого типа заключается в том, что их оболочка наполняется огнеопасным газом водородом. Воздушные шары, стратостаты, дирижабли, зонды поднимаются вверх за счёт того, что они наполнены газами, которые легче воздуха, и на них действует выталкивающая сила.
Кстати:
В июне 1893 г. канадский пароход «Порция» совершал рейс из порта Сент-Джон (Ньюфаундленд) в Нью-Брансвик. Мимо судна проплывали огромные ледяные горы — айсберги. Пассажиры захотели получше рассмотреть айсберг и уговорили капитана приблизиться к одному из них. «Порция» застопорила машины в 70 м от айсберга. Длина плавучей горы составляла почти 250 м, а высота — 60 м. Неожиданно ледяная глыба, искрящаяся на солнце, быстро отошла от парохода, и тотчас корпус судна содрогнулся от резкого толчка. Удивлённые матросы и пассажиры увидели, что пароход лежит на огромной льдине и с каждой секундой поднимается все выше и выше над поверхностью воды. Произошел невероятный случай! Известно, что время от времени айсберги переворачиваются. Пароход был подхвачен щелью в подводной части айсберга и оставался на вершине ледяной горы в течение нескольких минут. Потом айсберг пошатнулся и снова занял предыдущее положение, а судно благополучно оказалось в воде. Впрочем, не совсем благополучно: в его обшивке образовалась трещина, и «Порция» едва добралась до ближайшего порта.
- Заказать решение задач по физике
Условия плавания тел
Согласно закону Архимеда, на все тела, погруженные в жидкость, действуют выталкивающие силы, значение которых зависит от объемов этих тел и плотности жидкости. Таким образом, если тела имеют равные объемы, то и выталкивающие силы, действующие на них в данной жидкости, будут равными. Почему же тогда одни тела тонут в воде, а другие плавают?
Почему тела плавают или тонут
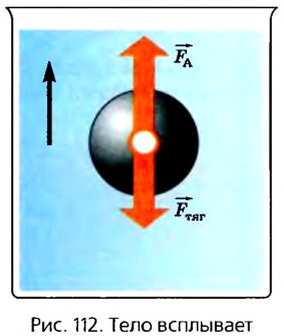
Для примера возьмем два шарика одинакового объема, но один металлический, а другой деревянный. Взвешивание их покажет, что вес деревянного шарика меньше веса металлического. Всплытие деревянного шарика, погруженного в жидкость, показывает, что равнодействующая силы тяжести и силы Архимеда направлена вверх, в направлении действия силы Архимеда. Таким образом, в этом случае сила Архимеда больше силы тяжести (рис. 112).
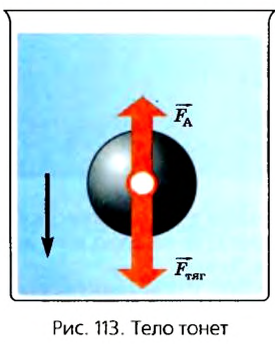
В случае с металлическим шариком равнодействующая направлена вниз, поскольку сила тяжести больше силы Архимеда (рис. 113).
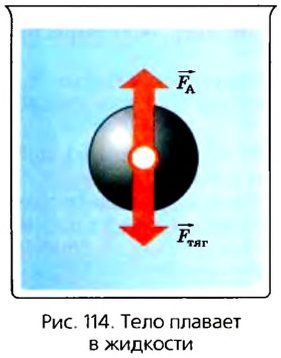
При равности сил Архимеда и тяжести, действующих на погруженное в жидкость тело, равнодействующая равна нулю (рис. 114). Следовательно, в этом случае погруженное в жидкость тело будет находиться в равновесии в любой точке жидкости.
Однако измерить силу тяжести или силу Архимеда во всех случаях невозможно или это неудобно. Поэтому предсказать поведение тела в жидкости можно не всегда. Чтобы найти выход, сделаем расчеты.
Когда тела тонут в жидкости
Тело тонет, если его средняя плотность больше плотности жидкости.
На каждое тело в жидкости действуют две силы: сила Архимеда 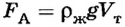
Для случая, когда тело тонет в данной жидкости:
Налитая в стакан с водой ртуть опускается на дно (рис. 115).
Подобным образом различные суда могут плавать по поверхности воды. Вес воды, вытесненной подводной частью судна, равен весу самого судна. Очевидно, что чем больший вес судна, тем больше глубина его погружения в воду.
Когда тела плавают в жидкости
Тело плавает, если его средняя плотность меньше плотности жидкости.
Если тело плавает, то
или
Отсюда
Налитое в стакан подсолнечное масло всплывает на поверхность воды, так как его плотность меньше плотности воды (рис. 116). Чтобы убедиться в этом, достаточно посмотреть в таблицу значений плотности на с. 53.
Плавание судов
Человек издавна мечтал о преодолении водного пространства. Сначала он приспосабливал для этого деревянные колоды, плоты, а затем начал строить деревянные лодки и корабли.
Для изготовления современных суден используют различные металлы. Из металла изготавливается корпус судна, его конструктивные элементы. Вместе с этим большой объем судна не заполнен металлом. Поэтому его средняя плотность меньше плотности воды.
При погружении нижней части судна в воду возникает сила Архимеда, равняющаяся весу вытесненной воды. При условиях плавания эта сила всегда равна весу судна. Если судно нагружают, его вес увеличивается, и оно начинает погружаться в воду. Чем глубже погружается судно, тем большей становится сила Архимеда. Когда она будет равной весу судна, оно прекращает погружаться. Глубину, на которую погружается судно в воду, называют осадкой судна.
Осадка судна зависит от его веса и массы груза, находящегося на судне. Увеличение массы груза приводит к увеличению осадки. Осадка уменьшается, когда судно переходит из реки в море, где плотность воды равна примерно 1030 кг/м3.
Осадка может изменяться только в определенных пределах, когда судно еще держится на поверхности воды. Чтобы контролировать осадку судна, на его борт наносят горизонтальную линию, которая получила название ватерлиния (от голландских слов water — вода и line — линия) (рис. 117). Значение силы Архимеда, когда судно погрузилось по ватерлинию, называют водотоннажностью судна.
Численно водотоннажность равна силе тяжести, действующей на судно с грузом. Самая большая водотоннажность у современных танкеров. Она достигает 5•106 кН и больше. Вместе с грузом масса этих суден 500 000 т и больше.
Если от водотоннажности вычесть вес судна, то получим вес груза, который это судно может перевезти. Это грузоподъемность судна.
Водный транспорт очень удобен и экономически выгоден. Перевозка грузов водным транспортом значительно дешевле, чем другими видами транспорта. Поэтому для дальнейшего его развития необходимо создавать более совершенные суда и одновременно заботиться о состоянии водных артерий страны, которым очень вредят промышленные выбросы и загрязнения (отходы) с судов.
Украина имеет развитый речной и морской флот. Самой большой судоходной рекой Украины является Днепр, фарватером которой плавают даже судна типа «река — море», которые выходят из реки в море, не перегружая груз.
- Гидростатическое взвешивание в физике
- Воздухоплавание в физике
- Машины и механизмы в физике
- Коэффициент полезного действия (КПД) механизмов
- Манометры в физике
- Барометры в физике
- Жидкостные насосы в физике
- Выталкивающая сила в физике
Описание процесса плавиния тел
Лодка из железа, спущенная на воду, плывёт, а эта же лодка, полностью погружённая в воду (затопленная), тонет. Из этого примера видно, что одно и тоже тело может плавать, а может и тонуть. Всё зависит от того, как тело приведено в контакт с жидкостью. Поэтому имеет смысл рассмотреть два случая взаимодействия тела с жидкостью.
Тело плавает в жидкости, т. е. находится в покое, частично погрузившись в жидкость. Это может быть любое тело, например, кусок дерева или катер. Важен сам факт плавания. При этом тело соприкасается только с жидкостью и воздухом, плавая предоставленным самому себе, свободно. На начальном этапе рассмотрения вопроса о плавании не будем учитывать вес вытесненного воздуха. На тело действует направленная вниз сила тяжести `F_sf»Т»` и направленная вверх сила Архимеда `F_sf»А»`. Поскольку сила тяжести `F_sf»Т»` равна весу тела (в вакууме), а сила Архимеда `F_sf»А»` – весу (в вакууме) вытесненной жидкости, то можно сказать, что вес тела равен весу вытесненной жидкости. При более строгом рассмотрении вопроса с учётом веса вытесненного воздуха можно показать, что вес тела в воздухе равен весу (тоже в воздухе) вытесненной жидкости.
Итак, если тело плавает в жидкости, то вес тела в воздухе равен весу в воздухе вытесненной им жидкости.
При решении задач, когда ситуация реальна, различием в весе в воздухе и вакууме обычно пренебрегают, приравнивая вес любого тела силе тяжести, действующей на тело.
Кусок льда объёмом V=0,1 м3V=0,1;mathrm м^3 плавает в воде. Найти объём `V_1` надводной части льда. Плотность воды ρ1=1 г/см3rho_1=1;mathrm г/mathrm{см}^3, плотность льда ρ2=0,9 г/см3rho_2=0,9;mathrm г/mathrm{см}^3.
Вес льдины `rho_2 Vg`, вес вытесненной воды `rho_1 (V — V_1)g`. По закону Архимеда `rho_2 Vg = rho_1 (V — V_1)g`. Отсюда
V1=ρ1-ρ2Vρ1=1-ρ2ρ1·V=0,01 м3V_1=dfrac{left(rho_1-rho_2right)V}{rho_1}=left(1-dfrac{rho_2}{rho_1}right)cdot V=0,01;mathrm м^3.
Тело полностью погружено в жидкость и отпущено. Возьмём в руки какое-нибудь тело (кусочек дерева, стальной болт), погрузим его полностью в жидкость (например, воду) и будем удерживать неподвижно. На тело со стороны Земли действует вниз сила тяжести FТ=ρТVgF_mathrm Т=rho_mathrm ТVg, а со стороны жидкости — вверх выталкивающая сила по закону Архимеда FА=ρЖVgF_mathrm А=rho_mathrm ЖVg. Здесь `V` — объём тела, ρТrho_mathrm Т и ρЖrho_mathrm Ж — плотность тела и жидкости. Отпустим тело. Если окажется, что $$F_mathrm Т;>;F_mathrm А$$, то тело начнёт двигаться вниз, т. е. тонуть. Если будет $$F_mathrm Т < F_mathrm А$$, то тело станет двигаться вверх, т. е. всплывать. После всплытия, когда тело будет плавать, объём погружённой в жидкость части тела окажется таким, что будет обеспечено равенство силы Архимеда (уже меньшей, чем величина $$ {F}_{mathrm{А}}$$) и силы тяжести $$ {F}_{mathrm{Т}}$$. Итак, тело будет плавать, если $$rho_mathrm ТVg;<;rho_mathrm ЖVg$$, т. е. $$rho_mathrm Т;<;rho_mathrm Ж$$.
Мы получили условие плавания тела: тело, предварительно полностью погружённое в жидкость, плавает в жидкости, если плотность тела меньше плотности жидкости.
Если плотности тела и жидкости равны, то полностью погружённое в жидкость тело может находиться в равновесии (покое) в любом месте жидкости, т. е. тело плавает внутри жидкости. Реально такая ситуация трудно осуществима, так как добиться строгого равенства плотностей нелегко.
Условие плавания сформулировано для тела, предварительно полностью погружённого в жидкость. Предварительное полное погружение важно, так как, например, металлическая миска, не полностью погружённая в воду, может плавать, а полностью погружённая утонет.
Условие плавания сформулировано для однородного тела, т. е. тела, плотность которого одинакова во всех точках тела. Это условие плавания справедливо и для неоднородного тела, например, куска льда с полостью внутри или стеклянной бутылки, заполненной частично водой и закрытой пробкой. В таком случае под плотностью тела надо понимать его среднюю плотность, т. е. отношение массы тела к его объёму.
В прошлых уроках мы познакомились с архимедовой силой и узнали о том, какие силы действуют в жидкости на погруженное в нее тело (архимедова сила и сила тяжести). Но разные тела ведут себя в жидкости по-разному: некоторые тонут, некоторые всплывают. Почему так происходит?
Какие условия провоцируют плавание? На этом уроке мы дополним свои знания о поведении тел, погруженных в жидкость.
Условия плавания тел
Рассмотрим ситуацию: мы полностью погружаем в жидкость тело и отпускаем его. Теперь на него действуют две противоположно направленные силы: сила тяжести и архимедова сила. Возможны три случая (рисунок 1).
При каком условии тело, находящееся в жидкости, тонет; плавает; всплывает?
Первый случай:
если сила тяжести $F_{тяж}$ больше архимедовой силы $F_A$, то тело будет двигаться ко дну — тонуть.
Если $F_{тяж} > F_A$, то тело тонет.
Второй случай:
если сила тяжести $F_{тяж}$ равна архимедовой силе $F_A$, то тело будет находиться в равновесии в любом месте жидкости.
Если $F_{тяж} = F_A$, то тело плавает.
Третий случай:
если сила тяжести $F_{тяж}$ меньше архимедовой силы $F_A$, то тело будет двигать вверх в жидкости — всплывать.
Если $F_{тяж} < F_A$, то тело всплывает.
Вес жидкости, вытесненной плавающим телом
Как показать на опыте, что вес жидкости, вытесненной плавающим телом, равен весу тела в воздухе?
Рассмотрим подробнее третий случай и проведем опыт: в сосуд с трубкой для отлива (отливной сосуд) нальем воду до уровня трубки. Возьмем плавающее тело, взвесим его в воздухе и погрузим его в воду (рисунок 2).
После этого из трубки выльется вода, объем которой равен объему погруженной части тела. Мы можем взвесить эту воду. Тогда мы увидим, что ее вес равен весу тела в воздухе.
Вес этой воды будет эквивалентен архимедовой силе, а вес тела в воздухе — силе тяжести. Точно такой же эксперимент можно провести в разных жидкостях — результат мы получаем одинаковый.
Почему так происходит?
Когда мы погрузили плавающее тело в воду, оно стало всплывать ($F_{тяж} < F_A$). Что будет происходить с точки зрения физики в тот момент, когда тело достигнет поверхности воды?
При последующем подъеме архимедова сила будет уменьшаться, потому что будет постепенно уменьшаться объем той части тела, которая погружена в воду.
Когда же будет выполнено условие $F_{тяж} = F_A$, то тело перестанет всплывать и будет держаться (плавать) на поверхности воды, частично погрузившись в нее.
Если тело плавает в жидкости, то вес вытесненной им жидкости будет равен весу этого тела в воздухе.
Условие плавания тел и плотность жидкости
Рассмотрим простой опыт, изображенный на рисунке 3.
Сначала опустим железную гирю в сосуд с водой (рисунок 3, а). Гиря тонет. А теперь опустим железную гирю в сосуд со ртутью (рисунок 3, б) — гиря всплыла. Это произошло, потому что плотность железа больше плотности воды, но меньше плотности ртути.
Выводы:
- Когда плотность твердого тела больше плотности жидкости, в которую его погружают, то тело тонет.
Если $rho_т>rho_ж$, то тело тонет.
- Когда плотность твердого тела меньше плотности этой жидкости, то оно всплывает:
Если $rho_т<rho_ж$, то тело всплывает.
- Когда плотность твердого тела равна плотности жидкости, то тело остается в равновесии внутри жидкости:
Если $rho_т=rho_ж$, то тело плавает.
Теперь взглянем на следующий опыт, представленный на рисунке 4.
Здесь мы погрузили в воду два одинаковых шарика: пробковый и парафиновый. Видно, что часть пробкового шарика, погруженная в воду, меньше той же части парафинового.
Как зависит глубина погружения в жидкость плавающего тела от его плотности?
Известно, что плотность пробки меньше плотности парафина. Можно сказать, что чем меньше плотность тела по сравнению с плотностью жидкости, тем меньшая часть тела погружена в жидкость.
Несмешивающиеся жидкости также будут находиться в одном сосуде в соответствии со своими плотностями: в нижней части сосуда более плотные, в верхней — более легкие (рисунок 5).
Плавание тел в природе
Почему водные животные не нуждаются в прочных скелетах?
В живой природе вес морских организмов почти полностью уравновешивается архимедовой силой, так как их плотность почти не отличается от плотности окружающей среды. Поэтому у морских животных легкие и гибкие скелеты, а у морских растений — эластичные стволы.
Каким образом рыбы могут менять глубину своего плавания и оставаться на ней? У каждой рыбы имеется плавательный (воздушный) пузырь (рисунок 6).
Какую роль играет плавательный пузырь у рыб?
Пузырь легко сжимается и расширяется: при увеличении глубины за счет мышечных усилий увеличивается давление воды на рыбу. Плавательный пузырь сжимается, и объем тела рыбы уменьшается, уменьшается величина архимедовой силы, и рыба может спокойно оставаться на выбранной глубине. То же самое происходит при уменьшении глубины, но в обратную сторону: пузырь расширяется, объем всего тела рыбы увеличивается.
Как регулируют глубину погружения киты?
Киты и другие морские млекопитающие используют для изменения глубины собственные легкие подобно плавательному пузырю у рыб.
Айсберг — это большой кусок льда, который свободно плавает в океане, так как плотность льда меньше плотности соленой воды (рисунок 7).
Обычно около $90 %$ объема айсберга находится под поверхностью воды, что делает столкновение с ним очень опасным. В 1912 году знаменитое судно «Титаник» столкнулось с айсбергом в Атлантическом океане. Оно затонуло, унеся с собой жизни 1513 пассажиров. Также айсберги являются огромными хранилищами пресной воды.
Упражнения
Упражнение №1
На весах уравновесили отливной сосуд с водой (рисунок 8, а). В воду опустили деревянный брусок. Равновесие весов сначала нарушилось (рисунок 8, б). Но когда вся вода, вытесненная плавающим бруском, вытекла из сосуда, равновесие весов восстановилось (рисунок 8, в). Объясните это явление.
Посмотреть ответ
Скрыть
Ответ:
На рисунке 8, б равновесие весов нарушилось из-за деревянного бруска. Вес на левой чаше весов увеличился на вес бруска.
Мы знаем, что если тело плавает в жидкости, то вес вытесненной им жидкости будет равен весу этого тела в воздухе. Значит, деревянный брусок вытеснил такое количество жидкости, которое равно его весу. Так весы снова пришли в равновесие.
Упражнение №2
На рисунке 9 изображено одно и то же тело, плавающее в двух разных жидкостях. Плотность какой жидкости больше? Почему? Что можно сказать о силе тяжести, действующей на тело, и архимедовой силе в том и другом случае?
Посмотреть ответ
Скрыть
Ответ:
Тело в обоих случаях плавает. Мы знаем, что плотность жидкости будет больше там, где наше тело погружено в жидкость меньше (его меньшая часть находится под водой). Значит, плотность жидкости больше во втором случае (рисунок 9, б).
Можно рассмотреть этот вопрос с другой стороны. Плавающее тело вытесняет такой объем жидкости, который равен весу этого тела в воздухе. В первом случае (рисунок 9, а) тело вытеснило больше жидкости, чем во втором. Но вес этих объемов жидкости будет одинаковый. Значит, больший объем жидкости будет иметь меньшую плотность.
Наше тело плавает и в первом, и во втором случае. Поэтому сила тяжести и архимедова сила будут равны друг другу (рисунок 10).
Кроме того, архимедова сила, действующая на тело в первом сосуде, будет равна архимедовой силе, действующей на тело во втором сосуде. Сила тяжести тоже одинакова для обоих случаев.
Как архимедова сила может быть одинаковой, если жидкости имеют разную плотность?
Сила Архимеда зависит не только от плотности жидкости, но и от объема погруженного в нее тела ($F_А = g rho_ж V_т$). Так, во втором сосуде плотность жидкости больше, но объем погруженной части тела меньше.
Упражнение №3
Яйцо тонет в пресной воде, но плавает в соленой (рисунок 11). Объясните почему. Пронаблюдайте это сами на опыте.
Посмотреть ответ
Скрыть
Ответ:
Яйцо тонет в пресной воде. Это означает, что в данном случае сила тяжести больше силы Архимеда.
В соленой воде яйцо будет плавать: сила тяжести и архимедова сила равны друг другу. Плотность соленой воды больше, чем плотность пресной. Это и есть причина увеличения архимедовой силы до величины силы тяжести и условия плавания тела: $F_А = g rho_ж V_т$, $F_А = F_{тяж}$.
Упражнение №4
Изобразите графически силы, действующие на тело, плавающее на воде, всплывающее на поверхность воды, тонущее в воде.
Посмотреть ответ
Скрыть
Ответ:
На рисунке 12:
- а — тело плавает: $F_А = F_{тяж}$;
- б — тело всплывает: $F_А > F_{тяж}$;
- в — тело тонет: $F_А < F_{тяж}$.
Упражнение №5
Пользуясь таблицами плотностей, определите, тела из каких металлов будут плавать в ртути, а какие — тонуть.
Посмотреть ответ
Скрыть
Ответ:
Когда плотность твердого тела равна плотности жидкости или больше нее, то тело плавает или всплывает. Если плотность тела будет больше плотности жидкости, то оно будет тонуть.
Плотность ртути составляет $13 space 600 frac{кг}{м^3}$. В таблице находим металлы с меньшей плотностью — они будут плавать:
- Свинец;
- Серебро;
- Латунь;
- Медь;
- Сталь;
- Железо;
- Олово;
- Цинк;
- Чугун;
- Алюминий.
Теперь найдем металлы, плотность которых больше плотности ртути. Они будут тонуть:
- Осмий;
- Иридий;
- Платина;
- Золото.
Упражнение №6
Будет ли кусок льда плавать в бензине, керосине, глицерине?
Посмотреть ответ
Скрыть
Ответ:
Для того, чтобы ответить на этот вопрос, нам нужно сравнить плотности приведенных жидкостей и плотность льда.
Плотность льда равна $900 frac{кг}{м^3}$, бензина — $710 frac{кг}{м^3}$, керосина — $800 frac{кг}{м^3}$, глицерина — $1260 frac{кг}{м^3}$.
Лед будет тонуть в бензине и керосине: $rho_л > rho_к > rho_б$.
А плотность глицерина больше плотности льда. Значит, лед будет в нем плавать (всплывать): $rho_л < rho_г$.
Упражнение №7
Объем погруженной в воду части айсберга составляет $100 space м^3$. Плотность льда равна $900 frac{кг}{м^3}$, плотность соленой воды равна $1030 frac{кг}{м^3}$. Найдите весь объем айсберга и его массу.
Дано:
$V_1 = 100 space м^3$
$rho_л = 900 frac{кг}{м^3}$
$rho_в = 1030 frac{кг}{м^3}$
$m-?$
$V-?$
Посмотреть решение и ответ
Скрыть
Решение:
Отметим на рисунке силы, действующие на айсберг: $F_A$ и $F_т$.
Сила $F_A$ приложена к центру погруженной в воду части айсберга и направлена вверх.
Сила $F_т$ приложена к центру тела айсберга и направлена вниз.
Так как айсберг плавает (не тонет и не всплывает до конца), он находится в состоянии равновесия:
$F_A = F_т$
$F_A = rho_{в}gV_1$
$F_т = mg$
$rho_{в}gV_1 = mg$
Отсюда найдем массу айсберга:
$m = rho_{в}V_1$,
$m = 1030 frac{кг}{м^3} cdot 100 space м^3 = 103 space 000 space кг = 103 space т$.
Из определения объема:
$V = frac{m}{rho_л}$,
$V = frac {103 space 000 space кг}{900 frac{кг}{м^3}} approx 114 space м^3$
Ответ: $m = 103 space т$, $V approx 114 space м^3$.
Задание
Французский ученый Декарт (1596−1650) для демонстрации некоторых гидростатических явлений придумал прибор (рисунок 13). Высокий стеклянный сосуд (банку) наполняли водой, оставляя сверху сосуда небольшой объем воздуха. В этот сосуд опускали небольшую полую стеклянную фигурку. Фигурку заполняли частично водой и частично воздухом так, чтобы она только немного выходила из воды. Сверху стеклянный сосуд плотно закрывали куском тонкой кожи. Нажимая на кожу, можно было заставить фигурку плавать в воде и на воде, а также тонуть.
Изготовьте такой прибор («картезианский водолаз») и проделайте с ним опыты. Фигурку замените небольшим поплавком (пипеткой), а сосуд закройте резиновой пленкой (рисунок 14). Объясните действие прибора. Продемонстрируйте на этом приборе законы плавания тел.
Посмотреть ответ
Скрыть
Ответ:
Изначально поплавок (пипетка) находится на поверхности жидкости (плавает). Когда мы нажимаем на резиновую пленку, это давление по закону Паскаля передается воздуху и воде внутри сосуда и пипетки. Воздух в пипетке сжимается, и она наполняется водой. Суммарная плотность пипетки в этот момент увеличивается. Увеличивается и сила тяжести, действующая на нее. Когда сила тяжести становится больше архимедовой силы, пипетка начинает тонуть.
Когда мы перестаем давить на резиновую пленку, сжатый воздух внутри нее снова расширится. Объем воды в пипетке уменьшится — уменьшится и сила тяжести. Теперь сила Архимеда больше силы тяжести, действующей на пипетку, — она снова всплывет на поверхность жидкости.

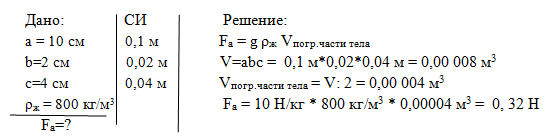



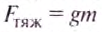
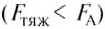 то тело будет всплывать (рис. 144, а). На поверхности оно будет плавать, частично погрузившись на глубину, которой достаточно для возникновения архимедовой силы, уравновешивающей вес тела.
то тело будет всплывать (рис. 144, а). На поверхности оно будет плавать, частично погрузившись на глубину, которой достаточно для возникновения архимедовой силы, уравновешивающей вес тела.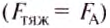 , то тело будет находится в равновесии в любом месте жидкости (рис. 144 ,б).
, то тело будет находится в равновесии в любом месте жидкости (рис. 144 ,б).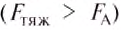 то тело утонет (рис. 144, в).
то тело утонет (рис. 144, в).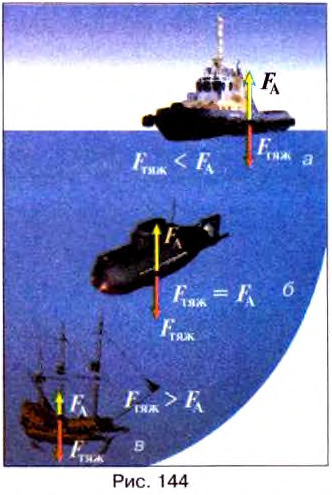
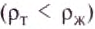 , то тело будет плавать на поверхности, частично погрузившись в воду.
, то тело будет плавать на поверхности, частично погрузившись в воду.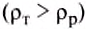 , то тело будет тонуть.
, то тело будет тонуть.