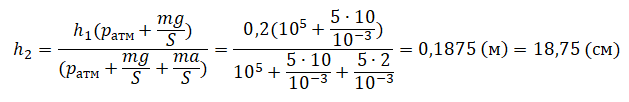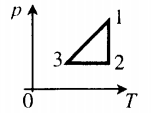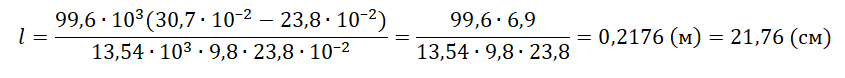Как найти первоначальную температуру газа

Часто в ходе какого-либо технологического процесса или при решении задач из курса термодинамики возникает необходимость ответить на вопрос: какова была начальная температура смеси газов, находившейся при определенных условиях (объеме, давлении и т.д.)

Инструкция

Предположим, заданы такие условия. Смесь трех газов: водорода, углекислого газа и кислорода, первоначально занимала сосуд объемом 22, 4 литра. Масса водорода составляла 8 г, масса углекислого газа – 22 г, а кислорода – 48 г. При этом парциальное давление водорода ровнялось примерно 4,05*10^5 Па, углекислого газа – 5,06*10^4 Па, а кислорода, соответственно – 3,04*10^5 Па. Требуется определить первоначальную температуру этой газовой смеси.

Прежде всего вспомните закон Дальтона, гласящий: общее давление смеси газов, находящейся в каком-то объеме, равно сумме парциальных давлений каждого из компонентов этой смеси. Сложите известные вам величины: 4,05*10^5 + 0,506*10^5 + 3,04*10^5 = 7,596*10^5 Па. Для упрощения расчетов примите округленное значение: 7,6*10^5 Па. Таково давление газовой смеси.

Теперь вам на помощь придет универсальное уравнение Менделеева-Клапейрона, описывающее состояние идеального газа. Разумеется, ни один из компонентов вашей смеси не является идеальным газом, но его вполне можно использовать в расчетах – погрешность будет очень невелика. Это уравнение записывается в такой форме: PV = MRT/m, где P – давление газа, V – его объем, R – универсальная газовая постоянная, M – фактическая масса газа, m – его молярная масса.

Но ведь у вас смесь газов. Как же быть в этом случае? Надо лишь немного преобразовать уравнение Менделеева-Клапейрона, записав его в таком виде: PV = (M1/m1 + M2/m2 + M3/m3) RT.

Легко можно понять, что если бы количество компонентов газовой смеси было равно 4, 5, 6 и т.д., уравнение преобразовывалось бы абсолютно аналогичным образом. Следовательно, искомая начальная температура газовой смеси вычисляется по формуле: Т = PV/(M1/m1 + M2/m2 + M3/m3)R.

Подставив в эту формулу известные вам значения (с учетом того, что величина R равна 8,31), и произведя вычисления, вы получите: 7,6*10^5* 0,0224 / (8,31 * 7,5) = 17024/62,325 = 273,15. Это значение температуры выражено, разумеется, в градусах Кельвина. То есть получается, что первоначально газовая смесь содержалась при температуре, равной 0 градусов по шкале Цельсия. Задача решена.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Предположим, заданы такие условия. Смесь трех газов: водорода, углекислого газа и кислорода,первоначально занимала сосуд объемом 22, 4 литра. Масса водорода составляла 8 г, масса углекислого газа – 22 г, а кислорода – 48 г. При этом парциальное давление водорода ровнялось примерно 4,05*10^5 Па, углекислого газа – 5,06*10^4 Па, а кислорода, соответственно – 3,04*10^5 Па. Требуется определить первоначальную температуру этой газовой смеси.

Источник

Как определить начальную температуру газа?

При нагревании газа до температуры 376 К средняя квадратичная
скорость его молекул увеличилась вдвое. Найти начальную температуру газа.

Решение.

Запишем формулу средней кинетической энергии молекулы газа.

m₀
– масса молекулы; <v_кв>
— средняя квадратичная скорость молекулы; k –
постоянная Больцмана; T
–
абсолютная температура газа.

Следовательно, T₁
= T₂/4
= 376/4 = 94,0 К.

Ответ: Начальная температура газа равна 94,0 К.

Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.

Источник

Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:

Определение

При постоянной массе газа и его неизменной молярной массе отношение произведения давления на объем к его абсолютной температуре остается величиной постоянной:

pVT=const или p1V1T1=p2V2T2

Объединенный газовый закон применительно к изопроцессам

Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.

Определение

Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным.

Изотермический процесс. Закон Бойля — Мариотта.

Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:

m = const (m₁ = m₂)

T = const (T₁ = T₂)

Для изотермического процесса действует закон Бойля — Мариотта:

Закон Бойля — Мариотта

Для газа данной массы произведение газа на его объем постоянно, если температура газа не меняется.

pV = const (p₁V₁ = p₂V₂)

Изохорный процесс. Закон Шарля.

Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:

m = const (m₁ = m₂)

V = const (V₁ = V₂)

Для изохорного процесса действует закон Шарля:

Закон Шарля

Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.

pT=const (p1T1=p2T2)

Изобарный процесс. Закон Гей-Люссака.

Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:

m = const (m₁ = m₂)

p = const (p₁ = p₂)

Закон Гей-Люссака

Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.

VT=const (V1T1=V2T2)

Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.

Так как газ нагревают, то:

T₂ – T₁ = 240 (К)

Отсюда:

T₂ = 240 + T₁ (К)

p₁ = p

p₂ = 1,6p

Запишем закон Шарля применительно к данному случаю:

pT1=1,6p240+ T1

Сделаем некоторые преобразования и вычислим начальную температуру:

pT1=1,6p240+ T1

240+ T1=1,6T1

0,6T1=240

T1=2400,6=400 (К)

Подсказки к задачам на газовые законы

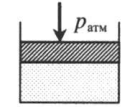	Газ под невесомым поршнем: p = p_атм p — давление газа; p_атм — давление, оказываемое на газ со стороны поршня.
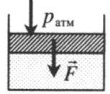	На невесомый поршень действует сила: p=pатм+FS F — сила, действующая на поршень; S — площадь поршня.
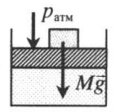	На невесомый поршень поставили груз. В данном случае на поршень дополнительно будет действовать сила тяжести: p=pатм+FтяжS=pатм+MgS F_тяж — сила тяжести, действующая на поршень со стороны груза; M — масса груза; g — ускорение свободного падения.
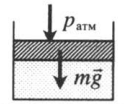	Газ под массивным поршнем. В данном случае на него дополнительно будет действовать сила тяжести поршня: p=pатм+mgS m — масса поршня.
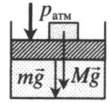	На массивный поршень поставили груз. В данном случае на поршень дополнительно будут действовать силы тяжести со стороны поршня и груза: p=pатм+MgS+mgS
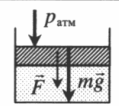	На массивный поршень действует сила. В данном случае газ сдавливается как атмосферным давлением, так и силой тяжести поршня, а также силой, которая на него действует: p=pатм+mgS+FS
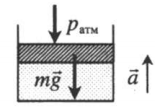	Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вверх. Когда ускорение движения лифта противоположно направлено ускорению свободного падения, вес тел увеличивается. Поэтому: p=pатм+mgS+maS a — модуль ускорения, с которым движется лифт.
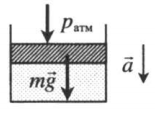	Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вниз. Когда ускорение движения лифта направлено в сторону вектора ускорения свободного падения, вес тел уменьшается. Поэтому: p=pатм+mgS−maS
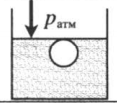	«Пузырек у поверхности воды» — на пузырек действует только атмосферное давоение: p = p_атм
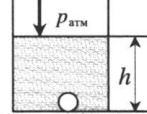	«Пузырек на глубине» — на пузырек действует атмосферное давление и давление столба жидкости: p = p_атм + ρgh ρ — плотность жидкости; h — глубина, на которой находится пузырек.
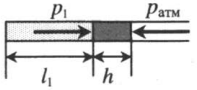	Газ, находящийся в горизонтальной пробирке, отделен от атмосферы столбиком ртути. Объем газа можно вычислить, используя параметры пробирки: V₁ = l₁S V₁ — объем газа; l₁ — длина части пробирки, которую занимает газ; S — площадь поперечного сечения пробирки. Давление газа равно атмосферному давлению: p₁ = p_атм
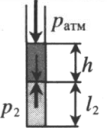	Пробирку поворачивают открытым концом вверх. В этом случае кроме атмосферного давления на газ давит давление со стороны ртути: P₂ = p_атм + ρgh Объем газа можно вычислить, используя параметры пробирки: V₂ = l₂S
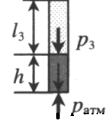	Пробирку поворачивают открытым концом вниз. В этом случае сумма давлений газа и ртути в пробирке равна атмосферному давлению. Отсюда давление газа равно: P₃ = p_атм – ρgh Объем газа можно вычислить, используя параметры пробирки: V₃ = l₃S
Шар или понтон поднимается вверх в воздухе или жидкости	Архимедова сила больше силы тяжести: F_A > F_тяж

Пример №2. Поршень площадью 10 см² массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с²? Изменение температуры газа не учитывать.

10 см² = 10^–3 м²

20 см = 0,2 м

100 кПа = 10⁵ Па

Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем:

p1=pатм+mgS

Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх:

p2=pатм+mgS+maS

Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно:

p₁V₁ = p₂V₂

Объемы в 1 и 2 случае будут определяться формулами:

V₁ = Sh₁

V₂= Sh₂

h₁ — расстояние от нижнего края поршня до дна сосуда в первом случае. h₂ — та же самая величина, но во втором случае (искомая величина).

Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов:

p1V1=Sh1(pатм+mgS)

p2V2=Sh2(pатм+mgS+maS)

Так как это изотермический процесс, правые части уравнений можно приравнять:

Sh1(pатм+mgS)= Sh2(p
атм+mgS+maS)

Отсюда:

Графики изопроцессов

Изопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.

Изопроцесс

График в координатах (p;V)

График в координатах (V;T)

График в координатах (p;T)

Изотермический (график — изотерма)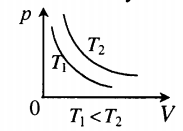

Изотерма в координатах (p;V) — гипербола. Чем ближе изотерма к началу координат и осям, тем меньшей температуре она соответствует.

Характер изменения переменных величин хорошо виден на графике.

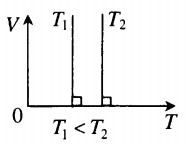
Изотерма в координатах (V;T) — прямая, перпендикулярная оси OT и параллельная оси OV. Чем ближе изотерма к оси OV, тем меньшей температуре она соответствует.

С увеличением объема давление уменьшается.

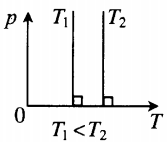
Изотерма в координатах (p;T) — прямая, перпендикулярная оси OT и параллельная оси Op. Чем ближе изотерма к оси Op, тем меньшей температуре она соответствует.

С увеличением давления объем уменьшается.

Изохорный (график — изохора)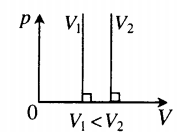

Изохора в координатах (p;V) — прямая, перпендикулярная оси OV и параллельная оси Op. Чем ближе изохора к оси Op, тем меньшему объему она соответствует.

С увеличением давления увеличивается температура.

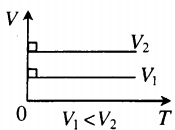
Изохора в координатах (V;T) — прямая, перпендикулярная оси OV и параллельная оси OT. Чем ближе изохора к оси OT, тем меньшему объему она соответствует.

С увеличением температуры увеличивается давление.

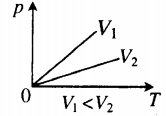
Изохора в координатах (p;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изохоры к оси OT, тем меньшему объему она соответствует.

Характер изменения переменных величин хорошо виден на графике.

Изобарный (график — изобара)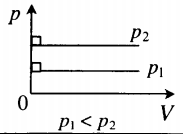

Изобара в координатах (p;V) — прямая, перпендикулярная оси Op и параллельная оси OV. Чем ближе изобара к оси OV, тем меньшему давлению она соответствует.

С увеличением объема температура растет.

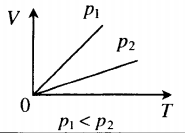
Изобара в координатах (V;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изобары к оси OT, тем меньшему давлению она соответствует.

Характер изменения переменных величин хорошо виден на графике.

Изобара в координатах (p;T) — прямая, перпендикулярная оси Op и параллельная оси OT. Чем ближе изобара к оси OT, тем меньшему давлению она соответствует.

С увеличением температуры объем растет.

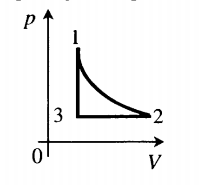
Пример №3. На рисунке представлен график циклического процесса. Вычертить его в координатах (p;T).

Определим характер изменения величин:

Процесс 1–2. Гипербола — это изотерма. Следовательно T₁₂ = const. В координатах (p;T) изотерма будет выглядеть как прямая, перпендикулярная оси OT.
Процесс 2–3. Прямая линия, перпендикулярная оси Op — это изобара. Следовательно p₂₃ = const. В координатах (p;T) изобара будет выглядеть как прямая, перпендикулярная оси Op.
Процесс 3–1. Прямая линия, перпендикулярная оси OV — это изохора. Следовательно V₃₁ = const. В координатах (p;T) изохора будет выглядеть как прямая, выходящая из начала координат.

Теперь, зная, какими будут графики всех величин в координатах (p;T), можно построить сам график. Он примет следующий вид:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17615

1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 2 раза. Какова первоначальная абсолютная температура газа?

Ответ:

а) 600 К

б) 400 К

в) 350 К

г) 300 К

Алгоритм решения

1.Записать исходные данные.

2.Определить вид изопроцесса.

3.Выбрать и записать подходящий для данного изопроцесса газовый закон.

4.Выполнить решение в общем виде.

5.Вычислить искомую величину.

Решение

Запишем исходные данные:

• Изменение температуры ∆T = 200 К.

• Первоначальный объем p₁ = 2p.

По условию задачи это изохорный процесс, следовательно он происходит в соответствии с законом Шарля:

p1T1=p2T2

Выразим конечную температуру и получим:

T₂ = T₁ – ∆T

Перепишем закон Шарля применительно к задаче и выразим первоначальную температуру:

2pT1=pT1−ΔT

2(T1−ΔT)=T1

2T1−T1=2ΔT

T1=2ΔT=2·200=400 (К)

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18859

В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l₁ = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l₂ = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения физических величин в СИ.

2.Определить вид изопроцесса и записать для него газовый закон.

3.Выполнить решение в общем виде.

4.Вычислить искомую величину.

Решение

Запишем исходные данные:

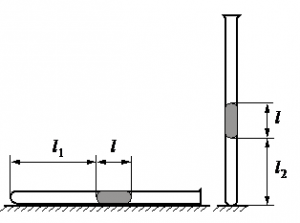
• Длина столбика воздуха под столбиком ртути в первоначальном состоянии: l₁ = 30,7 см.

• Длина столбика воздуха под столбиком ртути в конечном состоянии: l₂ = 23,8 см.

• Атмосферное давление: p_атм = 747 мм рт. ст.

30,7 см = 30,7∙10^–2 м

23,8 см = 23,8∙10^–2 м

1 мм рт. ст. = 133,322 Па

747 мм рт. ст. = 99,6∙10³ Па

Плотность ртути равна: ρ_рт = 13,54∙10³ кг/м³.

Так как процесс изменения состояния газа происходит при постоянной температуре, процесс можно считать изотермическим. Для него действует газовый закон Бойля — Мариотта:

p₁V₁ = p₂V₂

Первоначальное давление на столбик воздуха равно атмосферному давлению:

p₁ = p_атм

Конечное давление на столбик воздуха равно сумме атмосферного давления и давления, оказываемое силой тяжести столбика ртути:

p2=pатм+mртgS

S —площадь поперечного сечения трубки.

Масса ртути равна произведению плотности на объем столбика металла. Объем в свою очередь равен произведению длины столбика ртути на площадь поперечного сечения трубки. Поэтому:

p2=pатм+ρртVртgS=pатм+ρртlSgS=pатм+ρртlg

Первоначальный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:

V₁ = Sl₁

Конечный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:

V₂ = Sl₂

Выразив первоначальные и конечный величины, можем записать закон Бойля — Мариотта применительно к данной задаче:

pатмSl1=(pатм+ρртlg)Sl2

Преобразуем уравнение, выразим искомую величину и произведем вычисления:

pатмl1=pатмl2+ρртlgl2

ρртlgl2=pатмl1−pатмl2

l=pатм(l1−l2)ρртgl2

Ответ: 21,76

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18139

Паук-серебрянка медленно спускается на дно равномерно прогретого озера, неся между волосками брюшка пузырьки воздуха для своего подводного жилища. Какой процесс происходит с воздухом в пузырьках по мере погружения паука?

Ответ:

а) изобарное сжатие

б) изохорное нагревание

в) изотермическое сжатие

г) адиабатное сжатие

Алгоритм решения

Установить, какие величины меняются по мере погружения пузырьков воздуха на глубину.
Выяснить, какие величины сохраняются постоянными.
Установить вид изопроцесса.

Решение

Когда паук спускается в воде на глубину, давление постепенно увеличивается. На пузырьки воздуха будет действовать сумма атмосферного давления и давления столба воды. Под действием этого давления пузырек будет сжиматься. То есть, давление будет уменьшаться. Но само давление воздуха в пузырьке при этом будет равно давлению, оказываемому на него со стороны внешней среды. Следовательно, давление в пузырьке будет увеличиваться. При условии, что количество вещества в пузырьке при этом не меняется, величина температуры также должна оставаться постоянной. Это следует из уравнения состояния идеального газа. Следовательно, воздух в пузырьках претерпевает изотермическое сжатие.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 11.7k

Источник

Идеальный газ расширяется по закону PV2=const Найти первоначальную температуру газа, если при увеличении его объема в 3 раза температура оказалась равной 100 К.

Идеальный газ расширяется по закону PV²=const, где P – давление газа, V–занимаемый им объем. Найти первоначальную температуру газа, если при увеличении его объема в 3 раза температура оказалась равной 100 К.

(1)