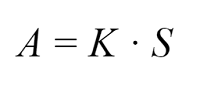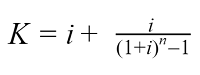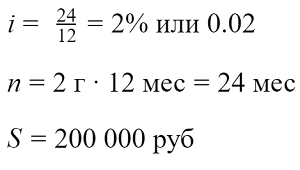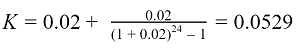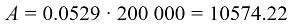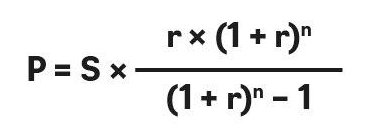Это слайд-шоу требует JavaScript.
Сущность простых процентов состоит в том, что процент по кредиту все время начисляется на первоначальную сумму кредита в течение всего срока действия кредита.
Например, если банк выдал клиенту в кредит 100 000 рублей на 2 года по ставке 10% годовых, то процент по кредиту и в первый и во второй год, при расчёте по формуле простого процента, составит 10 000 рублей (10 000*0,1).
К наращению простыми процентами прибегают при выдаче кредита сроком до 1 года или когда проценты не присоединяются к основной сумме долга, а периодически выплачиваются.
Для записи формулы простых процентов примем следующие обозначения:
I — сумма денежных средств, начисленных на первоначальную сумму по процентам за весь период (сумма с процентами — первоначальная сумма)
P — первоначальная сумма долга
S — сумма в конце срока (первоначальная сумма + сумма денежных средств по процентам)
i — процентная ставка, десятичная дробь. Например, если процентная ставка 20%, то в расчетах необходимо использовать 0,2 =20%/100
n — срок кредита в годах
Формула начисленных за весь срок процентов
I=Pni (I)
Формула простых процентов
S=P+I=P+Pni=P(1+ni) (II)
Вычисление первоначальной суммы долга по формуле простого процента
P=S/(1+ni) или P=S/(1+ni/100), если i измеряется в % (III)
Вычисление годовой процентной ставки по формуле простого процента
i=(S/P-1)/n или i=(S/P-1)/n*100, если необходимо получить процентную ставку (IV)
Вычисление срока кредита по формуле простого процента
n=(S/P-1)/i (V)
ПРАКТИКУМ
-
ВЫЧИСЛЕНИЕ СУММЫ НАКОПЛЕННОГО ДОЛГА ПО ФОРМУЛЕ ПРОСТЫХ ПРОЦЕНТОВ
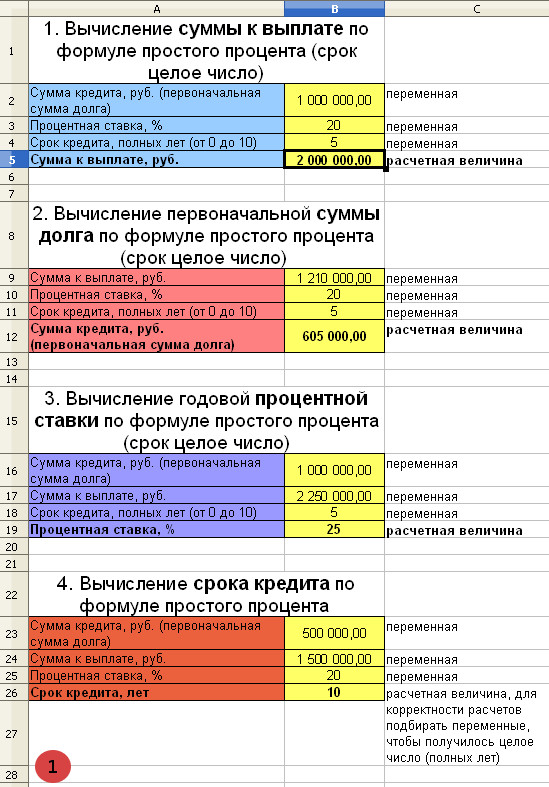
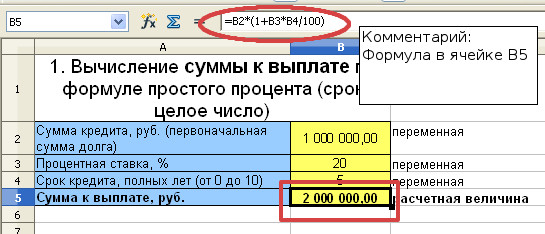
Банком выдан кредит в размере 1 000 000 рублей на 5 лет под 20% годовых. Необходимо определить сумму к погашению по кредиту по формуле простых процентов.
Первоначальная сумма кредита равна 1 000 000 рублей, P=1 000 000
Процентная ставка 20%, т.е. i=0,2
Срок кредита 5 лет, n=5
Сумма начисленных процентов за 5 лет по формуле простых процентов
I=Pni=1 000 000 * 5 *0,2=1 000 000
Сумма к выплате по кредиту
S=P+I=1 000 000 + 1 000 000=2 000 000 рублей
или
S=1 000 000(1+5*0,2)=2 000 000 рублей
-
ВЫЧИСЛЕНИЕ ПЕРВОНАЧАЛЬНОЙ СУММЫ ДОЛГА ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА
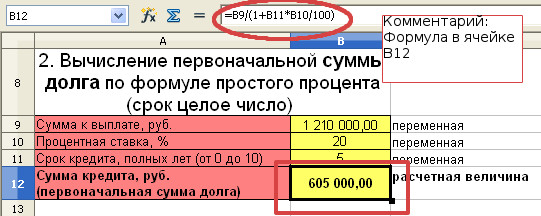
Клиент выплатил банку 1 210 000 рублей за кредит, который он взял на 5 лет назад под 20% годовых. Кредит рассчитывался по формуле простых процентов. Определить первоначальную сумму долга.
Сумма, выплаченная банку равна 1210 000 рублей, S=1 210 000
Процентная ставка 20%, т.е. i=0,2
Срок кредита 5 лет, n=5
Для расчёта первоначальной суммы кредита воспользуемся формулой (III)
P=S/(1+ni)=1 210 000/(1+5*0,2)=605 000 рублей
Пять лет назад банк выдал клиенту кредит в размере 605 000 рублей.
-
ВЫЧИСЛЕНИЕ ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА
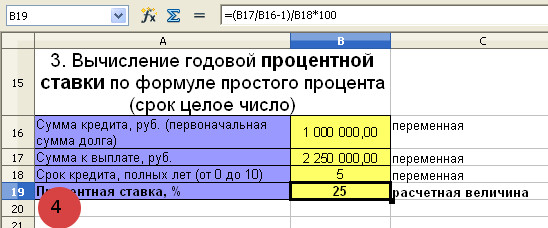
Банк выдал клиенту кредит в размере 1 000 000 рублей на 5 лет. Клиент вернул в банк 2 250 000 рублей. Определить годовую процентную ставку. В течение 5 лет процент начислялся на 1 000 000 рублей.
Первоначальная сумма кредита равна 1 000 000 рублей, P=1 000 000
Сумма, выплаченная банку равна 2 250 000 рублей, S=2 250 000
Срок кредита 5 лет, n=5
Для расчёта годовой процентной ставки по кредиту воспользуемся формулой (IV)
i=(S/P-1)/n=(2 250 000/1 000 000 – 1)/5=0,25 или 25%
Банк выдал кредит клиенту по ставке 25% годовых.
-
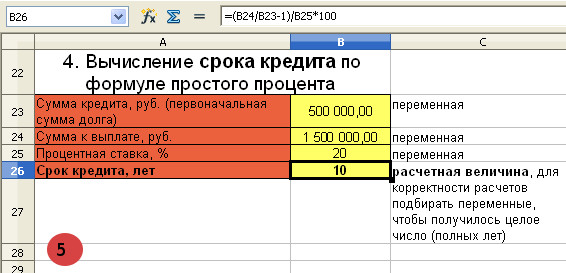
ВЫЧИСЛЕНИЕ СРОКА КРЕДИТА ПО ФОРМУЛЕ ПРОСТОГО ПРОЦЕНТА
Банк выдал клиенту кредит в размере 500 000 рублей под 20% годовых. Клиент обязался вернуть кредит, когда сумма с процентами достигнет 1 500 000 рублей. Через сколько лет клиенту нужно отдать кредит, рассчитанный по формуле простого процента?
Первоначальная сумма кредита равна 500 000 рублей, P=500 000
Сумма, выплаченная банку равна 1 500 000 рублей, S=1 500 000
Процентная ставка 20%, т.е. i=0,2
Для вычисления срока кредита воспользуемся формулой (V)
n=(S/P-1)/i=(1 500 000/500 000-1)/0,2=10 лет
Клиент должен заплатить банку 1 500 000 рублей через 10 лет.
Сделаем вычисления в OpenOffice Calc по формуле простого процента.
OpenOffice Calc
- Исходная таблица с расчетами простого процента
- Дополнительные настройки
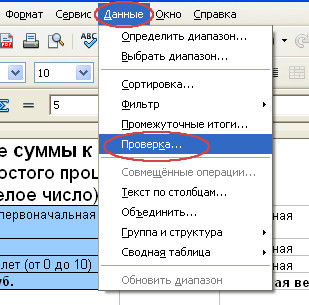
- Для корректности расчетов установим некоторые ограничения на вводимые в ячейку значения.
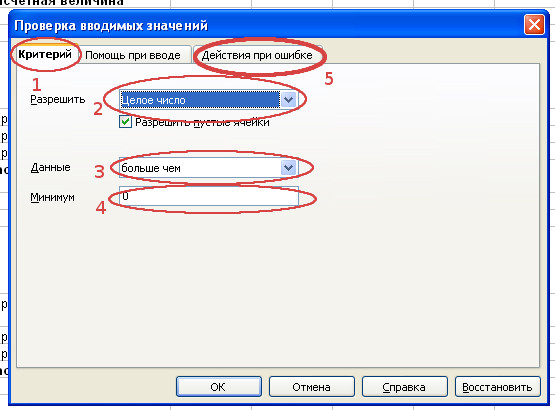
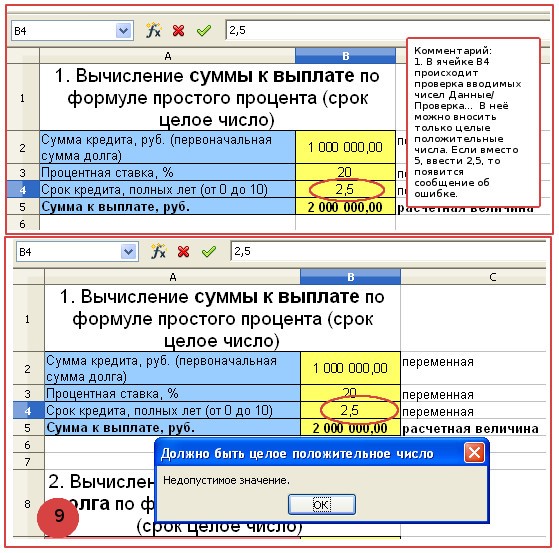
Например, сделаем так, чтобы в ячейку B4 можно было вводить только целые положительные числа. Для этого выделим ячейку B4 и вызовем диалоговое окно “Проверка вводимых значений”, последовательно выбрав Данные/Проверка…
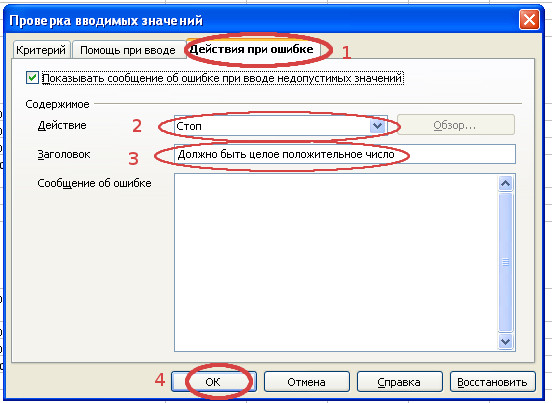
- Последовательно заполним все пункты диалогового окна “Проверка вводимых значений” в соответствии с примером.
- Проверим, как работают данные ограничения. Теперь при вводе в ячейку B4 неправильных значений, например, 2,5 вместо 5, появляется сообщение об ошибке и возвращается исходное значение 5.
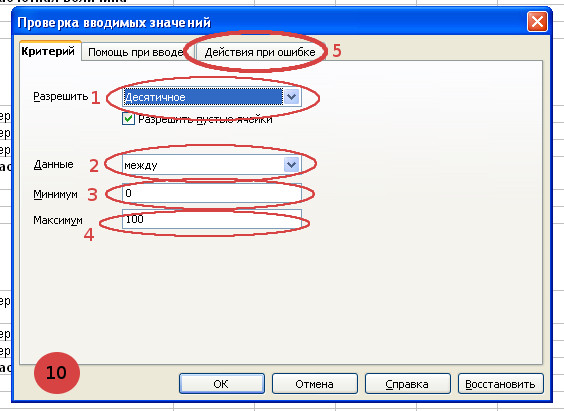
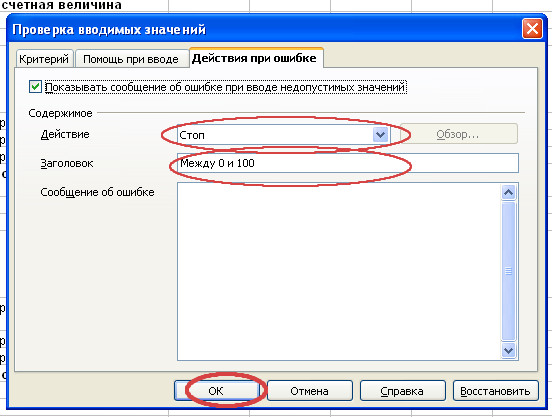
- Установим ограничения на вводимые значения для ячейки B3. Теперь в ячейку должны вводиться десятичные положительные значения в диапазоне от 0 до 100.
-
Если периоды начисления и ставки простых процентов для каждого периода одинаковые, то используется формула:
Дк = Дн x (1 + Т x α)N,
где N — общее число операций реинвестирования.
-
Если периоды начисления по продолжительности различны и каждому соответствует определенная простая ставка, то используется формула:
Дк = Дн x (1 + Т1 x α1) x (1 + Т2
x α2)x (1 + Т3
x α3)x …. x (1 + Тк
x αк).
Пример 47. По кредитному соглашению банк на сумму 100 тыс. руб. в течение месяца начисляет простые проценты по ставке 5% годовых. Определить наращенную сумму в течение полугодия.
Решение:
Значение Т равно шесть месяцев, рассчитываем исходя из 365 дней в году:
Дк = Дн x (1 + Т x α)N = 100 x (1 + 30 : 365
x 0,05)6 = 102,49 (тыс. руб.).
Наращенная сумма составит 102,49 тыс. руб., сумма наращения по простым процентам составит:
Сн = 102,49 — 100 = 2,49 тыс. руб.
Пример 48. Ссуда в размере 900 тыс. руб. предоставляется сроком на четыре года под простые проценты. Процентная ставка в первый год составляет 30%, каждый последующий год увеличивается на 5%. Определить сумму к погашению ссуды.
Решение:
Наращенная сумма к концу срока составит:
Дк = 900 x (1 + 0,3) x (1 + 0,35)x (1 + 0,40) x (1 + 0,45) = 3206,385 (тыс. руб.).
Сумма наращения по процентам:
Сн = 3206,385 — 900 = 2306,385 (тыс. руб.).
Сложные проценты.
В долгосрочных финансово-кредитных операциях, если суммы процентов не выплачиваются сразу после их начисления, а присоединяются к сумме долга, для наращения суммы ссуд применяют сложные проценты. Наращение по сложным процентам представляет собой последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме, которая служила базой для их определения, часто называют капитализацией процентов.
Наращенная сумма ссуды определяется по формуле:
Дк (Т) = Дн x (1 + α)Т,
где
Дк (Т) — наращенная сумма ссуды через Т лет;
Дн — первоначальная сумма;
α — годовая ставка процента в виде десятичной дроби;
Т — срок ссуды в годах.
Если в течение года начисления процентов осуществляются несколько раз, то наращенная сумма определяется по формуле:
Дк (Т) = Дн x (1 + α : М)(М x Т) ,
где
Дк (Т) — сумма ссуды к погашению через Т лет;
Дн — первоначальная сумма;
α — годовая процентная ставка;
М — количество начислений процентов в год;
М x Т — число единичных периодов от момента получения кредита до момента его погашения.
Единичный период — это промежуток времени между двумя начислениями (капитализация) процентов. Величина (α : М) называется номинальной ставкой. Чем больше начислений в год, тем чаще происходит капитализация.
Пример 49. Банк предоставил ссуду в размере 300 тыс. руб. сроком на два года под 28% годовых. Проценты начисляются каждое полугодие. Определить сумму к погашению ссуды.
Решение:
В данном примере количество единичных периодов — 4 (2 x 2), процентная ставка на полугодие (номинальная ставка) составит: 28% : 2 = 14%. Сумма средств к погашению через два года составит:
Дк(2) = 300 x (1 + 14 : 100)4 = 506,69 (тыс. руб.).
Пример 50. Банк предоставил ссуду в размере 600 тыс. руб. сроком на два года под 24% годовых, погашение кредита — каждый квартал. Определить наращенную сумму, сумму наращений на сложные проценты.
Решение:
В данном примере количество единичных периодов — 8 (2 x 4), процентная ставка на квартал составляет:
24% : 4 = 6%.
Сумма к погашению через два года составит:
Дк(2) = 600 x (1 + 6 : 100)8 = 956,31 (тыс. руб.).
Сумма наращения на сложные проценты составляет:
Сн = 956,31 — 600 = 456,31 (тыс. руб.).
Смешанные проценты.
Если период ссуды (Т) содержит несколько единичных периодов (МК) продолжительностью Тед и промежуток времени (Тн), продолжительность которого меньше чем продолжительность единичного периода (Тн < Тед), то ссуды выдаются под смешанные проценты. На целое количество единичных периодов (МК) начисляются сложные проценты, а на промежуток времени Тн, меньший продолжительности единичного периода — простые проценты:
Дк (Т) = Дн x (1 + α : М)мк x (1 + α x Тн : 360),
где
Дк (Т) — сумма ссуды к погашению по истечению срока кредита Т;
Дн — начальная сумма ссуды;
α — годовая процентная ставка;
М — количество единичных периодов в году;
МК — количество целых единичных периодов, вошедших в период кредитования;
Тн — количество дней, не вошедших в единичный период;
Ткр = МК x Тед + Тн.
Пример 51. Банк предоставил предприятию кредит в размере 250 тыс. руб. на 275 дней под 40% годовых. Определить сумму к погашению кредита, если погашение должно осуществляться ежеквартально.
Решение:
Продолжительность кредита — 275 дней можно представить в виде суммы продолжительности трех кварталов (каждый по 90 дней) и 5 дней.
В данном случае МК = 3, Тн = 5 дней, процентная ставка кредита на квартал равна 40% : 4 = 10%. Сумма средств к погашению кредита составит:
Дк (275) = 250 x (1 + 0,1)3 x (1 + 0,4 x 5 : 360) = 334,6 (тыс. руб.).
Банки используют смешанные проценты с целью максимизации своих доходов при предоставлении кредитов.
Эффективная (действительная) ставка процентов.
Если организации необходимо измерить реальный относительный доход, который получает организация от финансовой операции в целом за год, то для этого используют эффективную ставку. Расчет осуществляется по формуле:
αэ = (1 + α : М)м — 1.
Значение «αэ» определяется как процентное отношение дохода на капитал в конце года к величине капитала на конец года.
Пример 52. Банк начисляет на вклад проценты исходя из номинальной ставки 10% годовых. Определить эффективную годовую ставку при следующих условиях: начисления осуществляются каждый квартал, каждый месяц, каждый день.
Решение:
- Начисления каждый квартал в процентах:
αэ = [(1 + α : М)м — 1] x 100% = [(1 + 0,1 : 4)4 — 1] x 100% = 10,38%.
- Начисления каждый месяц в процентах:
αэ = [(1 + α : М)м — 1] x 100% = [(1 + 0,1 : 12)12 — 1] x 100% = 10,47%.
- Начисления осуществляются каждый день в процентах:
αэ = [(1 + α : М)M — 1] x 100% = [(1 + 0,1 : 365)365 — 1] x 100% = 10,52%.
Расчеты показывают, что размер эффективной ставки больше чем номинальной ставки, при росте количества начислений ее размер увеличивается.
Особенности наращения процентов в потребительском кредите.
В потребительском кредите простые проценты, как правило, начисляются на всю сумму кредита и присоединяются к основному долгу уже в момент выдачи кредита. Погашение долга с процентами производится частями, равномерно на протяжении всего срока кредита. Наращенная сумма долга по потребительскому кредиту (Дк) и сумма разового погасительного платежа (РДк) определяются по формуле:
Дк = Дн x (1 + Т x α) — РДк = Дк : (Т x М),
где
Т — срок потребительского кредита в годах;
М — число платежей в году.
Следует отметить, что фактическая процентная ставка оказывается заметно выше, чем ставка по условию потребительского кредита.
Пример 53. Банк предоставил кредит для покупки товара на сумму 600 тыс. руб. на два года, ставка простого годового процента 28%, погашение кредита в конце каждого месяца. Рассчитать сумму кредита к погашению, размер ежемесячного платежа.
Решение:
- Определим сумму, которая должна быть погашена в конце года:
Дк = Дн x (1 + Т x α) = 600 x (1 + 2 x 0,28) = 936 (тыс. руб.).
- Определим размер ежемесячного платежа:
РДк = Дк : (Т x М) = 936 : 12 = 78 (тыс. руб.).
Таким образом, каждый месяц заемщик должен платить по кредиту 78 тыс. руб. основного долга и платы за использование кредита.
Понятие дисконтирования и его использование в экономическом анализе
В финансовой практике часто приходится решать задачу, обратную наращенной сумме: по заданной сумме Дк, которую следует уплатить через некоторое время Т, необходимо определить сумму полученной ссуды Дн.
Такие ситуации возникают, когда руководство организации разрабатывает условия определенных контрактов, когда проценты с заданной суммы Дк удерживаются непосредственно при выдаче ссуды.
В этом случае говорят, что сумма Дк дисконтируется. Термин «дисконтирование» употребляется и как средство определения любой стоимостной величины Дк, вне зависимости от того, имела ли место в действительности финансовая операция (кредитование, выдача денег в долг и т.д.).
Основные понятия дисконтирования:
- учет — процесс начисления и удержания процентов вперед называется учетом;
- дисконт — проценты в виде разности между Дк и Дн:
Д = Дк — Дн;
- приведение стоимостного показателя — определение стоимостной величины будущего периода в настоящий момент времени.
Исходя из вида процентной ставки применяют два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет.
Математическое дисконтирование позволяет решать задачу: какую первоначальную сумму надо выдать в долг (Дн), чтобы при начислении на нее процентов ставке «α» к концу срока получить наращенную сумму, равную (Дк).
Для решения при начислении по простым процентам используется формула:
Дн = Дк x [1 : (1 + З x α)],
где
α — годовая ставка;
З = Тс : Т, Тс — период ссуды в днях;
Т — база распределения (360, 365 или 366 дней);
[1 : (1 + З x α)] называют дисконтным множителем, он показывает, какую долю составляет первоначальная ссуда Дн в наращенной сумме ссуды Дк.
Пример 54. Банк предоставил организации кредит под 15% годовых, по окончанию которого через 270 дней организация должна уплатить 450 тыс. руб. Определить, какую сумму получит организация, и сумму дисконта.
Решение:
- Определим сумму ссуды, которую может получить организация на этих условиях, считая, что временная база равна 365 дней:
Дн = Дк x [1 : (1 + З x α)] = 450 x [1 : (1 + 0,15 x 270 : 365)] = 450 x [1 : (1 + 0,11096)] = 450 x [1 : 1,11096] = 405,06 (тыс. руб.).
- Определим размер дисконта:
Д = Дк — Дн = 405,06 — 450 = -44,94 (тыс. руб.).
Банковский (коммерческий) учет.
Суть операции учета заключается в том, что банк до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца по цене, меньшей той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает обязательство с дисконтом. Получив при наступлении срока векселя деньги, банк, таким образом, реализует дисконт.
Проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды.
Простая годовая учетная ставка определяется по формуле:
d = (Дк — Дн) : Дк,
где d — годовая процентная ставка или дисконт.
Простая ставка процентов определяется по формуле:
α = (Дк — Дн) : Дн.
Пример 55. Если по условию договора платежное обязательство на сумму 400 тыс. руб. по окончании срока договора должно быть погашено за 430 тыс. руб., то размер годовой процентной ставки составит:
Д = (Дк — Дн) : Дк = (430 — 400) : 430 = 0,06977, или 6,98%.
Соответственно размер простой ставки процентов равен:
α = (Дк — Дн) : Дн = (430 — 400) : 400 = 0,075, или 7,5%.
Размер простой ставки процентов больше, чем размер годовой процентной ставки.
Размер дисконта или учета, удерживаемого банком, определяется из формулы:
Дн = Дк x (1 — Nс x d),
где
d — ставка дисконта;
Nc — доля дней до погашения кредита в базе распределения (чаще всего 360 дней);
(1 — Nc x d) — дисконтный множитель.
Пример 56. Вексель выдан на сумму 200 тыс. руб. с уплатой 19,10. Владелец векселя учел его в банке 5.09 по учетной ставке 9%. Определить сумму векселя к погашению, размер дисконта.
Решение:
Определим величину векселя к погашению, учитывая, что до срока погашения осталось 44 дня (292 — 248 = 44):
Дн = 200 x (1 — 44 : 360 x 0,09) = 200 x (1 — 0,01) = 200 x 0,99 = 198 (тыс. руб.).
Дисконт равен:
Д = Дк — Дн = 200 — 198 = 2 (тыс. руб.).
Оценка продолжительности срока ссуды и уровня процентной ставки.
При анализе условий контракта часто возникают задачи:
-
Определения срока ссуды или уровня процентной ставки при выполнении конкретных условий.
Расчет продолжительности ссуды в годах (Т) и днях (ДН) определяют по формулам:
Тг = (Дк — Дн) : (Дн x a) x Тд = Тг x 365 (дней);
Тг = (Дк — Дн) : (Дк x d) x Тд = Тг x 365 (дней),
где
Тг, Тд — соответственно, продолжительность ссуды в годах, днях;
Дк — размер долга, который следует уплатить через некоторое время Т;
Дн — сумма полученной ссуды;
d — ставка дисконта;
α — ставка процентов.
-
Определение уровня процентной ставки и ставки дисконта при заданных условиях: Дн, Дк, Тг.
Размер процентной ставки определяется по формуле:
α = (Дк — Дн) : (Дн x Тд) x Ту.
Размер учетной ставки определяется по формуле:
d = (Дк — Дн) : (Дк x Тд) x Ту,
где Ту — база начисления процентов Ту = 360 (365, 366).
Пример 57. Какова должна быть продолжительность ссуды в днях, чтобы по окончании договора о ссуде в размере 350 тыс. руб. выплатить по условию договора 380 тыс. руб., при условии, что на сумму долга начисляют простые проценты по ставке 13%.
Решение:
Продолжительность ссуды в годах равна:
Тг = (Дк — Дн) : (Дн x d) = (380 — 350) : (350 x 0,13) = 0,66 (года).
Продолжительность в днях: Тд = Т x 365 = 0,66 x 365 = 240,9 (дня).
Таким образом, срок ссуды при таких условиях должен составить 241 день.
Пример 58. При составлении контракта на ссуду в размере 400 тыс. руб. предусматривается погашение обязательств через 150 дней в размере 430 тыс. руб. Определить доходность данной операции для кредитора в виде учетной ставки и ставки процентов, расчетная база — 360 дней.
Решение:
Учетная ставка данной операции:
d = (Дк — Дн) : (Дк x Тдн) x 360 = (430 — 400) : (430 x 150) x 360 = 0,1674.
Таким образом, учетная ставка данной операции составляет 16,74%.
Ставка процентов по данной операции:
α = (Дк — Дн) : (Дн x Тд) x Ту = (430 — 400) : (400 x 150) x 360 = 0,18.
Таким образом, ставка процентов по данной операции составит 18%.
Содержание
- Как рассчитать аннуитетный платеж по кредиту
- Как рассчитать аннуитетный платеж
- Формула расчета аннуитета вручную
- Расчет графика платежей на компьютере
- Как выглядит кредитный калькулятор
- Аннуитет по кредиту — что это?
- Что такое аннуитет?
- Какие выделяют виды аннуитета?
- Формула расчета аннуитетного платежа
- Пример расчета аннуитетного платежа
- Переплата по кредиту
- Аннуитетный платёж
- Как рассчитать ежемесячный платёж?
- Пример расчёта аннуитетного платежа
- Кому выгоден аннуитет?
- Аннуитетный платеж по ипотеке: особенности и подводные камни
- Что такое аннуитетный платеж
- Как рассчитать ежемесячный взнос
- Плюсы и минусы аннуитетного платежа
- Как погасить кредит досрочно
Как рассчитать аннуитетный платеж по кредиту
Аннуитет — график погашения кредита, предполагающий выплату основного долга и процентов по кредиту равными суммами через равные промежутки времени. Это один из самых простых способов для расчета графика платежей, позволяющий точно определить сумму ежемесячных выплат и спланировать бюджет.
Для заемщика он удобен:
- равномерной и понятной финансовой нагрузкой — проще запомнить одну цифру, чем каждый раз носить с собой график платежей;
- доступностью — кредит c аннуитетом можно взять в любом банке;
- высокой вероятностью одобрения — требования к заемщикам мягче чем при выборе дифференцированного платежа.
Как рассчитать аннуитетный платеж
Есть несколько способов самостоятельно выполнить расчет аннуитетного платежа: вручную или в с помощью кредитного калькулятора. Для расчета надо знать всего три параметра: сумму, процентную ставку и срок займа.
При ручном подсчете с помощью обычного калькулятора или программы MS Excel вам придется самостоятельно выводить формулы и подставлять в них значения. на сайтах банков — простой и наглядный инструмент, который мгновенно пересчитывает сумму ежемесячного платежа при изменении суммы, ставки или срока кредита. Он позволяет быстро сравнить условия разных банков и продуктов и выбрать наиболее выгодное предложение.
Формула расчета аннуитета вручную
Формула выглядит так:
- Pеп — размер ежемесячного платежа,
- Oск — остаток суммы кредита,
- ПС — месячная процентная ставка (рассчитывается как ставка по кредиту /100 *12),
- ПП (-1) — процентные периоды до окончания срока кредита (в месяцах).
Для расчета возьмем кредит на сумму 20000 рублей под 12% годовых, оформленный на 36 месяцев.
Рассчитаем процентную ставку в месяц (ПС) = 12/(100*12) = 0,01
После выполнения расчетов получим:
Теперь можно определить переплату за весь период займа. Для этого размер ежемесячного взноса умножается на количество месяцев, а затем из полученного значения вычитают тело кредита — сумму основного долга, который вы получаете наличными.
Получается 3 904 руб.
Расчет графика платежей на компьютере
В Excel также можно выполнить расчет аннуитетного графика через финансовую функцию ПЛТ. Для этого нужно заполнить необходимые значения в мастере аргументов функции — окно появляется при нажатии кнопки fx.
Кпер — это срок кредита в месяцах, Пс — тело кредита.
Итоговым значением будет 664 руб., что аналогично результату ручного подсчета.
Как выглядит кредитный калькулятор
Выполнить действия гораздо быстрее и получить итоги в развернутом виде позволяют кредитные калькуляторы на банковских сайтах и финансовых ресурсах.
Стандартный калькулятор состоит из 4 ячеек, у каждой могут быть выпадающие списки:
- Тип платежей (с возможностью выбора аннуитетного или дифференцированного варианта).
- Размер кредита (в рублях).
- Ставка по кредиту в процентах (в год или месяц).
- Срок займа (в годах или месяцах).
Многие калькуляторы могут учитывать дату выдачи средств, досрочное погашение и другие дополнительные параметры.
Алгоритм действий простой:
- выбираем тип платежей «Аннуитетный»;
- вносим желаемую сумму в ячейку «Размер кредита»;
- прописываем приемлемую процентную ставку в ячейке «Ставка по кредиту»;
- указываем период кредитования (лучше в месяцах);
- нажимаем кнопку «Рассчитать».
Сервис рассчитает сумму ежемесячного взноса с разбивкой по основному долгу и процентами переплату. Итоги будут предложены в виде таблицы с графиком платежей.
Для наглядности вставим в ячейки калькулятора те же данные из предыдущего примера.
Калькулятор выдал сумму аннуитетного взноса в размере 664,29 руб. (второй столбец «Всего»).
Источник
Аннуитет по кредиту — что это?
Тенденции развития современного общества привели к тому, что те понятия, которые не так давно использовались главным образом в учебниках по экономической теории, стали все чаще встречаться в повседневной жизни. Одним из таких терминов является аннуитет, который все более активно стали использовать в сфере кредитования. Данный инструмент является достаточно выгодным, поэтому есть смысл познакомиться с его отличительными особенностями и способами расчета более подробно. Об этом и пойдет речь в данной статье.
Что такое аннуитет?
Аннуитет это — схема платежей, в соответствие с которой они производятся в одинаковом размере в соответствие с конкретным графиком выплат (а именно на постоянной основе через равные промежутки времени). Таким образом, можно представить аннуитет как поток одинаковых платежей, которые осуществляются через равные временные интервалы.
По аннуитетному виду платежа предполагается что выплаты осуществляются равными суммами через равные промежутки времени. Сумма аннуитетного платежа состоит из двух частей:
- Процентная часть, которая идет на оплату процентов пользования заемными средствами.
- Остаточная часть, которая направляется на оплату основного долга по кредиту.
Аннуитет позволяет сделать величину платежа, который включает в себя не только проценты за период, но и часть основного долга, постоянной. Это дает возможность плательщику заранее оценить свои силы и запланировать выплаты определенной суммы денежных средств в течение оговоренного срока.
Основным отличием от так называемого дифференцированного платежа является то, что при использовании последнего в первую очередь выплачивается полная сумма начисленных за использование кредитных средств процентов, а потом уже основной долг.
Отметим, что принцип аннуитета используется не только в кредитовании, но и для лизинговых платежей.
Какие выделяют виды аннуитета?
Для лучшего понимания использования аннуитета следует рассмотреть, какие его виды существуют. Так, можно отметить наличие следующей классификации:
- отложенный – в данном случае первая выплата производится в конце начального периода;
- немедленный – платеж осуществляется в начале нулевого периода.
Если говорить об аннуитете, используемом в сфере кредитования, то здесь имеет место отложенный аннуитет.
Кроме этого, распространенно выделение различных видов стоимости аннуитета, а именно:
- приведенная;
- будущая стоимость аннуитета.
Такое деление обусловлено стремлением определить максимально объективную ценность денежных средств, которые направлены на кредитование. Как будущая, так и текущая стоимость аннуитета рассчитывается определенным образом с использованием конкретных формул. Проводимый расчет текущей стоимости аннуитета зависит от ряда факторов.
Стоит отметить, что в силу теории о том, что с течением времени денежные средства могут обесцениваться в силу инфляции, имеет место такое понятие, как настоящая стоимость аннуитета. Также здесь играет роль упущенная выгода, ведь если бы кредитор оставил выданные денежные средства у себя, то он имел бы возможность получать доход в виде процентов по вкладу.
Формула расчета аннуитетного платежа
Формула аннуитетного платежа:
- A – ежемесячный аннуитетный платеж;
- K – коэффициент аннуитета;
- S – сумма кредита.
Расчет коэффициента аннуитета:
- K – коэффициент аннуитета;
- i – месячная процентная ставка по кредиту (годовая ставка деленная на 12 месяцев);
- n – количество периодов (месяцев), в течение которых выплачивается кредит.
Знание рассмотренной формулы позволяет провести требуемые расчеты, которые при наличии полных исходных данных не представляют собой особых сложностей. Очевидно, что для применения ее на практике необходимо учитывать некоторые принципиальные моменты. В их числе можно отметить, в первую очередь, принцип, по которому определяются доли основного долга и начисленных процентов в итоговом размере платежа. Для этого применяется определенная методика, которая предполагает прохождение несколько этапов расчета. Мы не будем на ней подробно останавливаться, отметим лишь общий принцип, в соответствии с которым производится расчет размера процентов и аннуитетного платежа, так же как и основного долга в виде разницы между этими двумя величинами для каждого месяца периода. При этом учитывается, что размер основного долга от месяца к месяцу снижается. Последний платеж требует отдельной корректировки в силу применения в процессе расчетов округлений.
Несмотря на равную величину платежей, соотношение суммы основного долга и начисленных процентов в их составе меняется. Если в начале основная доля приходится на проценты, то ближе к концу выплат остается погасить главным образом основную сумму долга.
Пример расчета аннуитетного платежа
Рассчитаем ежемесячный платеж по кредиту с аннуитетным графиком погашения под процентную ставку 24% годовых сроком на 2 года и на сумму 200 000 рублей.
Воспользуемся приведенными выше формулами:
Рассчитаем коэффициент аннуитета:
Теперь мы можем приступить к расчеты самого ежемесячного платежа. Подставим полученное значение коэффициента аннуитета:
Сумма ежемесячного платежа составила 10574.22 рублей.
Переплата по кредиту
Всего за 2 года банку будет выплачено 253 781.3 руб (10574.22 руб умноженные на 24 мес), а переплата составит 53781.3 руб.
Рассчитать кредит можно с помощью калькулятора кредита на нашем сайте.
Источник
Аннуитетный платёж
Аннуитетный платёж – это платёж, который устанавливается в равной сумме через равные промежутки времени. Так, при аннуитетном графике погашения кредита вы ежемесячно платите одну и ту же сумму, независимо от остатка задолженности. Другим способом внесения ежемесячных платежей является дифференцированный способ погашения.
Для сравнения, при дифференцированной схеме погашения кредита сумма основного долга выплачивается ежемесячно равными долями, а проценты рассчитываются от остатка задолженности. В таком случае сумма ежемесячного платежа уменьшается в процессе погашения кредита.
Например, сумма процентов за первый месяц пользования кредитом равна:
S%1 = S * i,
где S%1 – сумма процентов за первый месяц,
S — сумма кредита.
i — процентная ставка по кредиту в месяц (рассчитывается как годовая, делённая на 12 месяцев).
За второй и следующие месяцы:
S%n = (S — ∆S) * i,
где ∆S – сумма погашенного основного долга.
Как рассчитать ежемесячный платёж?
Формула расчёта суммы ежемесячного платежа при аннуитетной схеме погашения следующая:
A = K * S
где А – сумма ежемесячного аннуитетного платежа,
К — коэффициент аннуитета,
S — сумма кредита.
Сумма кредита известна. А для расчёта К – коэффициента аннуитета, используется следующая формула:
где i — процентная ставка по кредиту в месяц (рассчитывается как годовая, делённая на 12 месяцев),
n — количество периодов (месяцев) погашения кредита.
Применив вышеописанную схему расчёта, вы сможете узнать сумму, которую необходимо будет погашать ежемесячно.
Пример расчёта аннуитетного платежа
Предположим, что нужно провести расчёт ежемесячного платежа по кредиту с аннуитетным графиком погашения под процентную ставку 48% годовых сроком на 4 года на сумму 2 000 рублей. Используя приведённую выше формулу расчёта ежемесячного платежа (A = K • S) и коэффициента К, рассчитаем аннуитетный платёж.
Имеем:
i= 48%/12 месяцев = 4% или 0,04
n = 4 года* 12 месяцев = 48 (месяцев)
Рассчитываем К:
А теперь подставим полученное значение в формулу ежемесячного платежа:
А = 0,0472 * 2 000 = 94,4 рублей.
Таким образом, в течение 4 лет (или 48 месяцев) необходимо будет вносить в банк платёж в сумме 94,4 рублей. Переплата по кредиту за 4 года составит 2 531,2 ( = 94,4 * 48 – 2 000).
Кому выгоден аннуитет?
В первую очередь аннуитетный способ погашения выгоден банку. Объясняется это тем, что в течение всего срока погашения кредита проценты начисляются на первоначальную сумму кредита. При дифференцированной графике уплата процентов за 100% суммы кредита происходит только в первом месяце (в случае отсутствия отсрочки уплаты основного долга), далее проценты начисляются на остаток, из-за чего итоговая переплата по кредиту окажется меньше. Иными словами, среди двух кредитов с одинаковыми процентными ставками, сроком погашения и дополнительными комиссиями, кредит с аннуитетной схемой погашения всегда будет дороже.
Для примера, рассчитаем переплату по кредиту, рассмотренному выше, но теперь с дифференцированным графиком погашения. Она составит 1 960 рублей. Это на 571,2 рубля меньше, чем при аннуитетной схеме.
С другой стороны, погашение задолженности и процентов равными долями удобно кредитополучателю, так как ежемесячный платёж является постоянным и не требует уточнения в банке необходимой суммы взноса, в то время как при дифференцированном графике каждый месяц сумма платежа окажется разной.
Применение аннуитетного способа погашения, таким образом, обойдётся дороже, но при этом гораздо удобнее.
Источник
Аннуитетный платеж по ипотеке: особенности и подводные камни
Для многих людей ипотека — единственный способ обзавестись собственным жильем. Благодаря ей можно не тратить годы на то, чтобы накопить денег, и не переплачивать за аренду. Тем более что сегодня банки предлагают множество ипотечных программ на выгодных условиях, а государство регулярно выделяет средства на поддержку заемщиков и субсидирует льготные ставки. В 2020 году россияне оформили 1,7 млн жилищных кредитов на общую сумму 4,3 трлн руб. Это абсолютный рекорд за всю историю ипотечного рынка России, что говорит о востребованности ипотеки для решения квартирного вопроса.
При заключении ипотечного договора люди, как правило, всего смотрят на процентную ставку, сроки кредитования и размер первоначального взноса. Лишь немногие обращают внимание на способ погашения кредита. Между тем именно он определяет методику расчета ежемесячных платежей, а значит, и величину переплаты. Некоторые банки разрешают клиентам самим выбирать схему выплат — дифференцированную или аннуитетную. Они отличаются способом начисления и взимания процентов, а главное — итоговой суммой кредита. Мы выяснили, в чем заключаются плюсы и минусы аннуитета.
Что такое аннуитетный платеж
Это наиболее распространенная схема. При аннуитете ипотека выплачивается равными частями — размер взноса остается неизменным на протяжении всего периода кредитования. Сам платеж складывается из двух частей — основного долга (или тела кредита) и процентов, которые начисляются банком. Главная особенность в том, что в начале ежемесячный взнос практически полностью уходит на уплату процентов, тогда как основной долг заемщика не уменьшается. Постепенно это соотношение выравнивается: если первое время вы гасите в основном проценты, то потом средства идут в счет задолженности.
Так банк себя подстраховывает: он получает проценты авансом и почти ничего не теряет, даже если ипотека выплачивается раньше срока. При дифференцированной системе в начале заемщик делает крупные ежемесячные взносы, но с каждым месяцем их размер уменьшается. Это происходит за счет того, что тело кредита гасится равными частями на протяжении всего периода кредитования, а уже поверх фиксированной суммы начисляются проценты. При досрочном погашении ипотеки переплата будет меньше: разница особенно ощутима при больших суммах и сроках кредитования.
Как рассчитать ежемесячный взнос
Оформляя ипотеку, важно реально оценивать свои финансовые возможности и просчитывать бюджет на годы вперед. Специалисты говорят, что ежемесячные выплаты не должны превышать 40% от совокупного дохода семьи. В противном случае придется экономить на повседневных нуждах. График платежей обычно составляется вместе с банком при заключении договора. И все же при желании вы можете предварительно рассчитать сумму ежемесячного взноса с помощью ипотечных калькуляторов и онлайн-сервисов, размещенных на сайтах банков.
Расчетная формула выглядит так:
- P — аннуитетный платеж по кредиту,
- S — запрашиваемая сумма займа,
- r — процентная ставка (в месяц),
- n — срок кредита в месяцах.
Рассмотрим простой пример. Итоговые цифры будут приблизительными, поскольку в каждом банке свои условия по графику и выплате взносов, но расчет в большинстве случаев одинаковый. Допустим, вы решили взять ипотеку на 3 млн руб. на пять лет под 10% годовых. При аннуитете вы будете платить по 63,74 тыс. руб. каждый месяц, а общая сумма процентов составит 824,47 тыс. руб.
Если же вы выбрали дифференцированную схему погашения, ежемесячный платеж на протяжении кредитного периода будет опускаться от 75 тыс. до 50,412 тыс. руб. А итоговая переплата окажется существенно меньше — 762,5 тыс. руб.
Плюсы и минусы аннуитетного платежа
У аннуитетных платежей есть преимущества. Прежде всего, это простота. Аннуитет более удобен в бытовом смысле — заемщик точно знает, какую сумму нужно вносить каждый месяц, и может заранее планировать бюджет. Намного легче запомнить одну цифру, чем постоянно сверяться с графиком платежей. Аннуитет также подходит тем, кто хочет уменьшить размер ежемесячного взноса, растянув платежи по кредиту на более продолжительный период. Но помните, что при увеличении срока кредита растет и сумма переплаты.
Важное преимущество аннуитета — его доступность. Ипотеку с такой схемой погашения можно оформить в любом банке. А требования к заемщику будут мягче, чем при выборе дифференцированного платежа. Поскольку ежемесячный взнос по аннуитету всегда меньше первого взноса по дифференцированной системе, вы можете брать более крупные суммы. Дело в том, что в первую очередь банки обращают внимание на соотношение платежа с доходами потенциального заемщика. Аннуитет повышает доступность кредитных продуктов, особенно если речь о крупном долгосрочном займе.
Но из-за переплаты по процентам кредит с аннуитетной схемой всегда дороже, и с этой точки зрения заемщику выгоднее дифференцированные платежи. Основной недостаток дифференцированной схемы — высокие стартовые взносы. Чем больше сумма и меньше срок кредита, тем ощутимее разница. Если доходы позволяют платить ежемесячные взносы большими суммами, лучше выбирать дифференцированную систему. Если же вы не готовы платить больше на начальном этапе, вам подойдет аннуитет.
Как погасить кредит досрочно
Зная о переплатах при аннуитете, многие ипотечные заемщики задумываются о том, чтобы погасить кредит досрочно — если не полностью, то хотя бы частично. Такую возможность дают все российские банки. Клиент может выбрать — сократить либо сумму ежемесячного платежа, либо срок кредита. Чтобы не ошибиться, заранее продумайте, что для вас важнее — заплатить банку меньше денег или снизить свои текущие расходы. Например, уменьшая срок погашения, вы минимизируете общую переплату. Это логично: чем меньше заемщик пользуется кредитом, тем меньше процентов он платит.
Если уменьшить ежемесячный взнос, вы сразу получите свободные средства. Существует и третий вариант — самый оптимальный. Специалисты рекомендуют уменьшать обязательный платеж, но при этом продолжать выплачивать полную сумму, установленную первоначально. Во-первых, так вы сократите срок погашения. Во-вторых, при появлении материальных трудностей вы сможете снизить финансовую нагрузку и платить только минимальный обязательный платеж. Такая схема позволяет уменьшать срок ипотеки и переплату тогда, когда это комфортно для бюджета.
Минус такой комбинированной схемы в том, что переплата по процентам будет больше, чем при сокращении срока. Какой бы варианты вы ни выбрали, имейте в виду: при аннуитетных платежах выгода от досрочного погашения всегда будет напрямую зависеть от оставшегося срока кредита. То есть чем ближе его конец, тем менее выгодно погашать ипотеку досрочно.
Источник
Российские банки раньше часто придумывали сомнительные схемы по привлечению клиентов – обещали низкие ставки по кредитам, которые оказывались намного более высокими. С 2008 года проблему решили – банки теперь обязаны указывать полную стоимость кредита с учетом всех дополнительных платежей. И благодаря этому показателю любой клиент может легко понять, какую сумму он переплатит банку, если оформит кредит. Как рассчитывается полная стоимость кредита и что о ней стоит знать клиенту – расскажем в этой статье.
Содержание статьи
- 1 Что такое «полная стоимость кредита»?
- 2 Что входит, а что не входит в полную стоимость кредита?
- 3 Как рассчитывается полная стоимость кредита?
- 4 Пример расчета ПСК – как правильно?
- 5 Зачем заемщику знать ПСК?
- 6 Выводы
Что такое «полная стоимость кредита»?
Если банк в рекламе предлагает беспроцентную рассрочку или кредит под 0% годовых, то, по логике, ежемесячный платеж рассчитывается простым делением суммы кредита на его срок. А если по кредитной карте долгий льготный период, то и по ней клиент должен отдавать только то, что взял. По факту, однако, это не совсем так – и если клиент откроет договор на пункте «Полная стоимость кредита», там будет какая-то цифра больше нуля. А часто – намного больше нуля.
Формально полная стоимость кредита – это те затраты, которые понесет клиент по кредитному договору, выраженные в процентах от первоначальной суммы кредита. То есть, полная стоимость кредита – это окончательная и бесповоротная переплата заемщика.
Впервые полную стоимость кредита банки начали указывать с 2008 года, таким было требование закона, а до этого указывалась эффективная ставка процента. По сути, это похожие величины, но впоследствии расчет уточнили – ведь банки начали выдумывать все новые и новые уловки (вроде страховки и удорожания кредита при отказе от нее).
Полная стоимость кредита в обязательном порядке должна быть указана в кредитном договоре – будь это потребительский кредит, кредитная карта, автомобильный или ипотечный кредит. Более того, полная стоимость кредита – это не то же самое, что процентная ставка по нему:
- процентная ставка по кредиту – это процент, который платит заемщик банку за пользование кредитными средствами;
- полная стоимость кредита – учитывает как процентную ставку, так и дополнительные платежи, которые должен будет сделать заемщик. Например, это может быть обязательная или добровольная страховка, стоимость обслуживания кредитной карты или стоимость оформления закладной по ипотечному кредиту.
Говоря проще, полная стоимость кредита – это все, что заплатит «сверху» основной суммы заемщик, который будет гасить кредит по графику.
Что входит, а что не входит в полную стоимость кредита?
Главная задача расчета полной стоимости кредита (ПСК) – показать заемщику окончательную сумму его переплаты, если он будет следовать всем правилам и графику платежей. То есть, в нее входят все обязательные платежи по кредиту, с которыми столкнется клиент.
Как следует из федерального закона «О потребительском кредите (займе)», в расчет полной стоимости кредита включаются платежи:
- по погашению основной суммы кредита (формально это не переплата, все дело в формуле подсчета, о ней дальше);
- по уплате процентов по кредитному договору;
- другие обязательные платежи в адрес кредитора, если они предусмотрены договором (например, если есть комиссия за выдачу кредита, и т.д.);
- в случае потребительского кредита на карту – стоимость обслуживания карты;
- платежи в пользу третьих лиц, если они предусмотрены условиями договора;
- сумма страховой премии по договору страхования – но только если при страховом случае выплату получит не заемщик, а другое лицо (то есть, банк);
- сумма страховой премии по договору добровольного страхования, если от наличия или отсутствия страховки зависят условия кредита (сейчас почти всегда отсутствие страховки повышает процентную ставку по кредиту).
По прочим платежам и платежам в адрес третьих лиц закон делает оговорку: если на момент заключения договора сумма таких платежей точно не известна, то в полной стоимости кредита учитывается сумма, актуальная на данный момент.
Не включаются в полную стоимость кредита платежи, которые заемщик несет не по желанию банка, или за нарушение условий договора. Такими платежами могут быть:
- платежи, которые обусловлены требованиями законодательства, а не условиями договора (например, обязательное страхование объекта недвижимости по ипотеке). Отдельно прописаны и платежи в счет страхования объекта залога по потребительскому кредиту;
- платежи, которые заемщик вносит как штрафные санкции за нарушение условий договора (никто заранее не знает, просрочит ли заемщик платеж);
- платежи, которые зависят от решения заемщика (например, если в условиях договора есть комиссия за досрочное погашение долга – оплачивая кредит по графику, заемщик ее не платит);
- платежи по дополнительным услугам, которые никак не влияют на шансы получить кредит и на его условия, и от которых можно отказаться в течение 14 дней после оформления (то есть, финансовая защита и другие варианты страховок);
- плата за валютные операции (курсовые разницы) или комиссия за снятие наличных с карты (заемщик при желании может их не снимать, а проводить оплату).
Конкретный перечень платежей, которые учитываются или не учитываются в полной стоимости кредита, можно найти на сайтах банков – просто потому, что разные банки делают разные услуги обязательными или добровольными к оплате клиентом.
Например, «Альфа-Банк» включает в полную стоимость автокредита расходы на полис КАСКО, но не включает расходы на ОСАГО. А по ипотеке включает и оформление залога, и оформление аккредитива, и регистрацию закладной, услуги нотариуса, и плату за страховку.
Как рассчитывается полная стоимость кредита?
На первый взгляд, все очень просто – нужно сложить сумму платежей по графику, отнять от полученного значения первоначальную сумму кредита, разделить на число лет (или на число месяцев, а потом умножить на 12).
Но так как кредиты бывают разные, как и способы их погашения, в законе предусмотрена более сложная формула для расчета. Начинается она не очень сложно:
где:
ПСК – полная стоимость кредита в процентах годовых
i – процентная ставка базового периода (не в процентах, а в десятичной дроби)
ЧБП – число базовых периодов в течение года (год всегда равен 365 дням)
Сложнее всего рассчитать процентную ставку базового периода – ведь это может быть день, месяц, квартал или целый год.
В законе прописана громоздкая формула – это уравнение, в котором нужно найти наименьшее положительное решение:
где:
ДПк – сумма денежного потока в конкретный период. В данном случае поток может быть как со знаком минус (выдача кредита), так и со знаком плюс (его погашение). Именно поэтому в расчете учитывается и погашение основной суммы
qk – количество полных базовых периодов с момента выдачи кредита до текущего момента
ek – срок, который пройдет от завершения прошлого базового периода до даты платежа
m – количество денежных потоков. Сюда входит и выдача кредита, и его погашение (то есть, для кредита на 12 месяцев это будет 13 платежей)
Как можно понять их курса математики, нужно решить достаточно объемное уравнение, определив процентную ставку – то есть, значение i. А ноль в конце уравнения означает, что по итогам кредит должен быть полностью погашен.
Пример расчета ПСК – как правильно?
Нет смысла рассчитывать ПСК вручную, даже банки делают все это исключительно в автоматическом режиме. А в домашних условия расчет можно сделать в Excel, например, через функцию ВСД (внутренняя ставка доходности).
Посчитаем на примере: взят кредит на сумму в 400 000 рублей на срок в 2 года с погашением аннуитетными платежами раз в месяц, ежемесячный платеж составляет 19 017 рублей (последний – 19 010,52 рублей).
Если посчитать все по старинке:
- сумма всех платежей – 456 402 рубля;
- переплата за весь срок – 56 402 рубля;
- переплата за месяц – 2 350 рублей, или 0,5875% от суммы кредита;
- стоимость кредита за год – 7,05% годовых.
Это будет совсем неточный расчет – ведь кредит погашается по аннуитетной схеме, когда проценты «капают» на остаток долга, но распределены так, что в начале погашаются больше проценты, а потом – основная сумма.
Используем Excel, функцию ВСД с данными [-400000; 19017; 19017;…;19017; 19010,52]. Получим значение в 1,083% (то есть, 0,01083)– это ставка за базовый период, то есть, месяц:
По формуле ПСК получаем такую полную стоимость кредита:
ПСК = 0,01083 × 12 × 100 = 12,996%
Учитывая, что при расчете ВСД было небольшое округление, полная стоимость кредита в данном случае составляет 13% годовых.
Зачем заемщику знать ПСК?
Изначально требование указывать полную стоимость кредита появилось в законе из-за того, что некоторые банки слишком часто шли на хитрости, заманивая клиентов сверхнизкими процентными ставками (например, 0,01% годовых), но взимали с них дополнительные платежи (вроде 2-3% от суммы кредита в месяц за расчетное обслуживание).
ПСК позволяет точно понять, какой процент от первоначальной суммы кредита переплатит клиент – причем уже с учетом навязанной или обязательной страховки, комиссионных сборов, стоимости обслуживания по карте, и всеми остальными платежами.
И если менеджер банка по какой-то причине начнет требовать от клиента-заемщика оплатить что-то еще (например, подписку на СберПрайм или подписку на юридические или медицинские консультации), можно будет совершенно четко понять – это незаконное требование.
В ряде случаев клиент может заплатить меньше, чем ПСК – например, если он будет грамотно пользоваться льготным периодом по карте, сделает разовый платеж для снижения ставки по ипотеке или найдет способ оформить страховку по кредиту в сторонней компании и сэкономить на этом. Но как только банк пытается взять что-то сверх ПСК, клиент должен понимать – ему пытаются навязать что-то необязательное, от чего можно смело отказываться.
Выводы
ПСК – это полная стоимость кредита, представляющая собой сумму, которую клиент обязан вернуть банку. В нее входит не только основной долг и сумма процентов по нему, но и всевозможные дополнительные комиссии и платежи.
Рассчитать сумму кредита можно как самостоятельно (для чего нужно хорошо знать математику), воспользоваться онлайн-калькулятором или занести все данные в Excel.
Знание полной стоимости кредита позволит сэкономить на тех дополнительных услугах, которые банк выдает за обязательные, но которые таковыми не являются.
Содержание материала
- Почему важно считать кредит самому?
- Видео
- Как рассчитать годовые проценты по кредиту?
- Как самостоятельно рассчитать аннуитетный платеж
- Какие данные нужны для расчета платежа по кредиту
- Воспользуемся банковскими калькуляторами
- Виды ежемесячных выплат по кредитам
- Самостоятельный подсчет при аннуитетных платежах
- Из чего состоит ежемесячный платеж
- Формула расчета процентов по кредиту
- Какие данные нужны для расчета
- Пример расчета процентов по кредиту
- Погашать долг можно по-разному
- Как составить график платежей
- График выплаты кредита с аннуитетными платежами
- График выплаты кредита с дифференцированными платежами
Почему важно считать кредит самому?
Кредитами сейчас сложно кого-то удивить. Каждый среднестатистический россиянин имеет или имел как минимум один-два кредита в своей жизни или собирается его взять. Если вы идете в банк для получения кредита и вам дают несколько предложений, то нужно выбрать самое дешевое и выгодное для вас. Для этого нужно рассчитать кредит самому, например в Excel. Нужно также знать размер ежемесячного платежа, чтоб понять нагрузку займа на ваш бюджет. Это тоже можно сделать самостоятельно.
Видео
Как рассчитать годовые проценты по кредиту?
Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:
10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.
При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.
То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.
При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.
Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.
Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.
Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.
Как самостоятельно рассчитать аннуитетный платеж
Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.
Стандартная формула расчета аннуитетного платежа выглядит так:
Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.
А вот как рассчитывается коэффициент аннуитета:
Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.
Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.
Количество платежей равно количеству месяцев — 18.
Подставляем данные в формулу и считаем коэффициент аннуитета:
0,0125 × (1 + 0,0125)18 / ((1 + 0,0125)18 − 1) = 0,062385
Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.
Какие данные нужны для расчета платежа по кредиту
Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.
Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:
- ставка,
- размер желаемого займа,
- срок, на который вы хотите занять деньги.
Воспользуемся банковскими калькуляторами
Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.
Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.
Виды ежемесячных выплат по кредитам
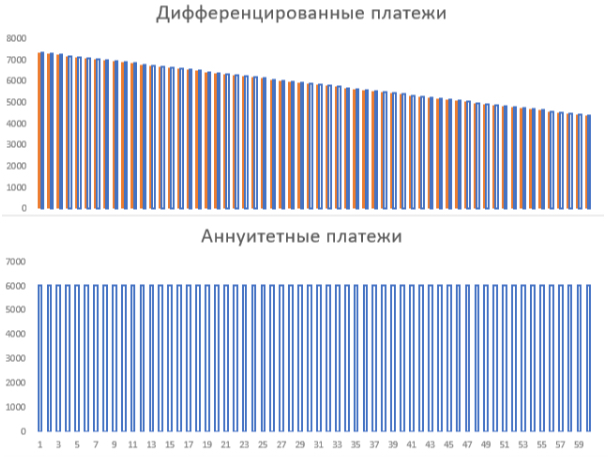
Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.
Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.
В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.
Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.
Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.
Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.
Самостоятельный подсчет при аннуитетных платежах
Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:
- Процентная ставка — 18%.
- Период кредитования — 24 месяца.
- Сумма кредита — 500000 рублей.
Классическая формула для расчета аннуитетного платежа выглядит так:
Разовый аннуитетный платеж = Сумма кредита * Ка
где Ка — это коэффициент аннуитета.
Ка = ((ЕПС* (1 + ЕПС)n)/( (1 + ЕПС)n -1)
где ЕПС — ежемесячная процентная ставка.
Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.
Итоговый расчет примет вид:
500 000 * (0,015 * (1 + 0,015)24)/((1 + 0,015)24 -1) = 24 962,05 рублей в месяц.
Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.
Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:
24 962,05 * 24 = 599 089,24 рублей.
Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.
Из чего состоит ежемесячный платеж
Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.
Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.
Формула расчета процентов по кредиту
S = (s3 x i x Kk / Kr) / 100
- S = вычисляемые проценты;
- S3 = общая сумма кредита;
- i = процентная ставка по кредиту;
- Kk = кол-во дней по платежам;
- Kr = кол-во дней на календарный год.
Какие данные нужны для расчета
- Сумма, выданная в кредит;
- Процентная ставка за год;
- Кол-во календарных дней в текущем году.
Пример расчета процентов по кредиту
65000 рублей – сумма переплаты в год. Для того чтобы посчитать сумму переплаты в месяц нужно 65000 рублей разделить на 12.
Погашать долг можно по-разному
Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.
С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.
Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.
Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.
Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).
, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.
Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.
Как составить график платежей
Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.
Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.
Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.
При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р.
В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.
Сначала считаем проценты:
Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году
Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р.
Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р.
Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р.
На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).
Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.
График выплаты кредита с аннуитетными платежами
| Номер платежа | Сумма платежа | Сумма в погашение тела кредита | Сумма платежа в погашение процентов | Остаток долга |
|---|---|---|---|---|
| 1 | 18 715,44 | 15 016,81 | 3698,63 | 284 983,19 |
| 2 | 18 715,44 | 15 084,83 | 3630,61 | 269 898,37 |
| 3 | 18 715,44 | 15 387,92 | 3327,51 | 254 510,44 |
| 4 | 18 715,44 | 15 473,04 | 3242,39 | 239 037,40 |
| 5 | 18 715,44 | 15 670,17 | 3045,27 | 223 367,24 |
| 6 | 18 715,44 | 16 053,39 | 2662,05 | 207 313,85 |
| 7 | 18 715,44 | 16 074,31 | 2641,12 | 191 239,53 |
| 8 | 18 715,44 | 16 357,69 | 2357,75 | 174 881,84 |
| 9 | 18 715,44 | 16 487,49 | 2227,95 | 158 394,35 |
| 10 | 18 715,44 | 16 762,63 | 1952,81 | 141 631,73 |
| 11 | 18 715,44 | 16 911,09 | 1804,35 | 124 720,64 |
| 12 | 18 715,44 | 17 126,53 | 1588,91 | 107 594,11 |
| 13 | 18 715,44 | 17 388,93 | 1326,50 | 90 205,18 |
| 14 | 18 715,44 | 17 566,25 | 1149,19 | 72 638,93 |
| 15 | 18 715,44 | 17 819,89 | 895,55 | 54 819,04 |
| 16 | 18 715,44 | 18 017,06 | 698,38 | 36 801,98 |
| 17 | 18 715,44 | 18 246,59 | 468,85 | 18 555,40 |
| 18 | 18 768,91 | 18 555,39 | 213,51 |
Первый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 016,81
Сумма платежа в погашение процентов
3698,63
Остаток долга 284 983,19
Второй платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 084,83
Сумма платежа в погашение процентов
3630,61
Остаток долга 269 898,37
Третий платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 387,92
Сумма платежа в погашение процентов
3327,51
Остаток долга 254 510,44
Четвертый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 473,04
Сумма платежа в погашение процентов
3242,39
Остаток долга 239 037,40
Пятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
15 670,17
Сумма платежа в погашение процентов
3045,27
Остаток долга 223 367,24
Шестой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 053,39
Сумма платежа в погашение процентов
2662,05
Остаток долга 207 313,85
Седьмой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 074,31
Сумма платежа в погашение процентов
2641,12
Остаток долга 191 239,53
Восьмой платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 357,69
Сумма платежа в погашение процентов
2357,75
Остаток долга 174 881,84
Девятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 487,49
Сумма платежа в погашение процентов
2227,95
Остаток долга 158 394,35
Десятый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 762,63
Сумма платежа в погашение процентов
1952,81
Остаток долга 141 631,73
Одиннадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
16 911,09
Сумма платежа в погашение процентов
1804,35
Остаток долга 124 720,64
Двенадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 126,53
Сумма платежа в погашение процентов
1588,91
Остаток долга 107 594,11
Тринадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 388,93
Сумма платежа в погашение процентов
1326,50
Остаток долга 90 205,18
Четырнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 566,25
Сумма платежа в погашение процентов
1149,19
Остаток долга 72 638,93
Пятнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
17 819,89
Сумма платежа в погашение процентов
895,55
Остаток долга 54 819,04
Шестнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
18 017,06
Сумма платежа в погашение процентов
698,38
Остаток долга 36 801,98
Семнадцатый платеж
Сумма платежа
18 715,44
Сумма в погашение тела кредита
18 246,59
Сумма платежа в погашение процентов
468,85
Остаток долга 18 555,40
Восемнадцатый платеж Сумма платежа 18 768,91 Сумма в погашение тела кредита 18 555,39 Сумма платежа в погашение процентов 213,51 Остаток долга
При дифференцированном платеже проценты в первом месяце будут такими же — 3698,63 Р. Дальше же принцип расчета процентов аналогичен, а сумма основного долга будет каждый месяц уменьшаться равномерно — на 16 666,67 Р (300 000 / 18). Ежемесячный платеж будет складываться из этих двух сумм.
В результате в первые месяцы платеж будет больше, чем при аннуитетном способе, а итоговая переплата будет меньше.
График выплаты кредита с дифференцированными платежами
| Номер платежа | Сумма платежа | Сумма в погашение тела кредита | Сумма платежа в погашение процентов | Остаток долга |
|---|---|---|---|---|
| 1 | 20 365,30 | 16 666,67 | 3698,63 | 283 333,33 |
| 2 | 20 276,26 | 16 666,67 | 3609,59 | 266 666,67 |
| 3 | 19 954,34 | 16 666,67 | 3287,67 | 250 000,00 |
| 4 | 19 851,60 | 16 666,67 | 3184,93 | 233 333,33 |
| 5 | 19 639,27 | 16 666,67 | 2972,60 | 216 666,67 |
| 6 | 19 248,86 | 16 666,67 | 2582,19 | 200 000,00 |
| 7 | 19 214,61 | 16 666,67 | 2547,95 | 183 333,33 |
| 8 | 18 926,94 | 16 666,67 | 2260,27 | 166 666,67 |
| 9 | 18 789,95 | 16 666,67 | 2123,29 | 150 000,00 |
| 10 | 18 515,98 | 16 666,67 | 1849,32 | 133 333,33 |
| 11 | 18 365,30 | 16 666,67 | 1698,63 | 116 666,67 |
| 12 | 18 152,97 | 16 666,67 | 1486,30 | 100 000,00 |
| 13 | 17 899,54 | 16 666,67 | 1232,88 | 83 333,33 |
| 14 | 17 728,31 | 16 666,67 | 1061,64 | 66 666,67 |
| 15 | 17 488,58 | 16 666,67 | 821,92 | 50 000,00 |
| 16 | 17 303,65 | 16 666,67 | 636,99 | 33 333,33 |
| 17 | 17 091,32 | 16 666,67 | 424,66 | 16 666,67 |
| 18 | 16 858,45 | 16 666,67 | 191,78 |
Первый платеж
Сумма платежа
20 365,30
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3698,63
Остаток долга 283 333,33
Второй платеж
Сумма платежа
20 276,26
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3609,59
Остаток долга 266 666,67
Третий платеж
Сумма платежа
19 954,34
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3287,67
Остаток долга 250 000,00
Четвертый платеж
Сумма платежа
19 851,60
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
3184,93
Остаток долга 233 333,33
Пятый платеж
Сумма платежа
19 639,27
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2972,60
Остаток долга 216 666,67
Шестой платеж
Сумма платежа
19 248,86
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2582,19
Остаток долга 200 000,00
Седьмой платеж
Сумма платежа
19 214,61
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2547,95
Остаток долга 183 333,33
Восьмой платеж
Сумма платежа
18 926,94
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2260,27
Остаток долга 166 666,67
Девятый платеж
Сумма платежа
18 789,95
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
2123,29
Остаток долга 150 000,00
Десятый платеж
Сумма платежа
18 515,98
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1849,32
Остаток долга 133 333,33
Одиннадцатый платеж
Сумма платежа
18 365,30
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1698,63
Остаток долга 116 666,67
Двенадцатый платеж
Сумма платежа
18 152,97
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1486,30
Остаток долга 100 000,00
Тринадцатый платеж
Сумма платежа
17 899,54
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1232,88
Остаток долга 83 333,33
Четырнадцатый платеж
Сумма платежа
17 728,31
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
1061,64
Остаток долга 66 666,67
Пятнадцатый платеж
Сумма платежа
17 488,58
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
821,92
Остаток долга 50 000,00
Шестнадцатый платеж
Сумма платежа
17 303,65
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
636,99
Остаток долга 33 333,33
Семнадцатый платеж
Сумма платежа
17 091,32
Сумма в погашение тела кредита
16 666,67
Сумма платежа в погашение процентов
424,66
Остаток долга 16 666,67
Восемнадцатый платеж Сумма платежа 16 858,45 Сумма в погашение тела кредита 16 666,67 Сумма платежа в погашение процентов 191,78 Остаток долга