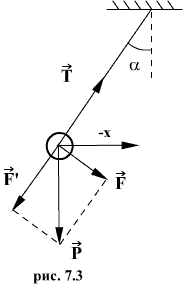
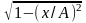Физическим
маятником
называется твердое тело, закрепленное
на неподвижной горизонтальной ocи (оси
подвеса), не проходящей через центр
тяжести, и совершающее колебания
относительно этой оси под действием
силы тяжести.
Вывод
периода:
При небольших углах отклонения α (рис.
7.4) физический маятник так же совершает
гармонические колебания. Будем считать,
что вес физического маятника приложен
к его центру тяжести в точке С. Силой,
которая возвращает маятник в положение
равновесия, в данном случае будет
составляющая силы тяжести – сила F.
Знак
минус в правой части означает то, что
сила F направлена в сторону уменьшения
угла α. С учетом малости угла α
.
Используем основное уравнение динамики
вращательного движения
.
Момент силы: определить в явном виде
нельзя. С учетом всех величин, входящих
в исходное дифференциальное уравнение
колебаний физического маятника имеет
вид
.
Решение
этого уравнения
Определим
длину l математического маятника, при
которой период его колебаний равен
периоду колебаний физического маятника,
т.е. 
или
.
Из этого соотношения определяем
.
Данная формула определяет приведенную
длину физического маятника, т.е. длину
такого математического маятника, период
колебаний которого равен периоду
колебаний данного физического маятника.
21.23.
Выведите уравнение колебательного
движения, являющегося суперпозицией
гармонических колебаний одного
направления с близкими частотами.
Изобразите результирующее колебание
на графике. Как называется такой вид
колебания?
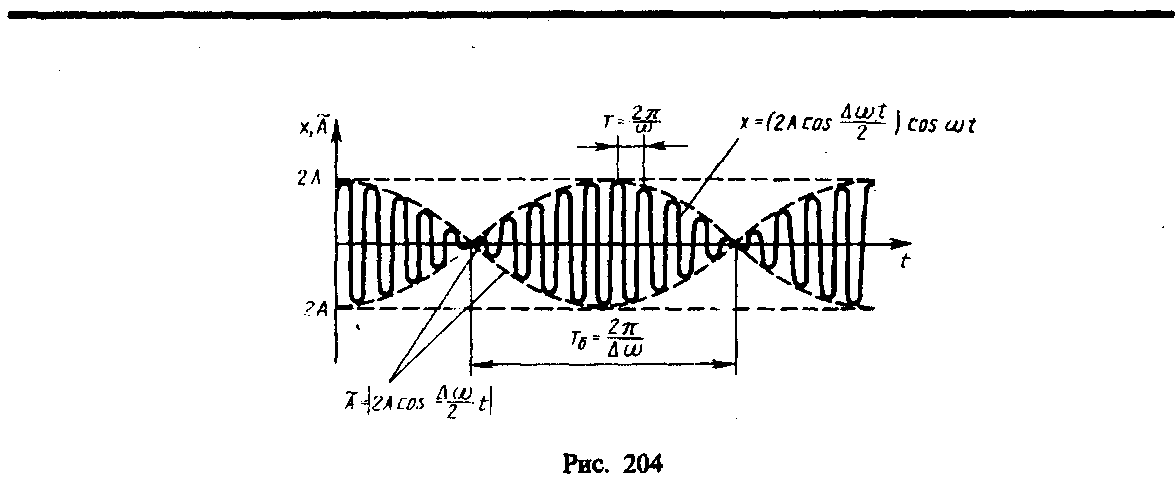
Для
практики особый интерес представляет
случай, когда два складываемых
гармонических колебания одинакового
направления мало отличаются по частоте.
В результате сложения этих колебаний
получаются колебания с периодически
изменяющейся амплитудой. Периодические
изменения амплитуды колебания, возникающие
при сложении двух гармонических колебаний
с близкими частотами, называются
биениями. Пусть амплитуды складываемых
колебаний равны А, а частоты равны
и +,
причем <<.
Начало отсчета выберем так, чтобы
начальные фазы обоих колебаний были
равны нулю:
Складывая эти выражения и учитывая, что
во втором сомножителе /2<<,
найдем
(144.3).
Результирующее колебание (144.3) можно
рассматривать как гармоническое с
частотой ,
амплитуда Аб,
которого изменяется по следующему
периодическому закону:
(144.4).
Частота изменения Аб
в два раза больше частоты изменения
косинуса (так как берется по модулю),т.
Е. частота биений равна разности частот
складываемых колебаний:
Период биений
22.Сложение
взаимно-перпендикулярных гармонических
колебаний. Получите уравнение траектории
частицы, колеблющейся по осям х и у с
одинаковой частотой. Каковы траектории
при колебаниях по взаимно перпендикулярным
осям с кратными частотами?
Рассмотрим
результат сложения двух гармонических
колебаний одинаковой частоты ,
происходящих во взаимно перпендикулярных
направлениях вдоль осей х и у. Для
простоты начало отсчета выберем так,
чтобы начальная фаза первого колебания
была равна нулю, и запишем
(145.1),
где
— разность фаз обоих колебаний, А и В —
амплитуды складываемых колебаний.
Уравнение траектории результирующего
колебания находится исключением из
выражений (145.1) параметра t.
Записывая складываемые колебания в
виде
и заменяя во втором уравнении cost
на х/А и sint
на
,
получим после несложных преобразований
уравнение эллипса, оси которого
ориентированы относительно координатных
осей произвольно:
(145.2)
Так
как траектория результирующего колебания
имеет форму эллипса, то такие колебания
называются эллиптически поляризованными.
25.
Какие силы называют квазиупругими?
Каков характер движения тела под
действием этих сил? Запишите дифференциальное
уравнение гармонических незатухающих
колебаний и его решение. Выведите формулу
для расчета периода.
КВАЗИУПРУГАЯ
СИЛА —
направленная к центру О сила. модуль
к-рой пропорционален расстоянию r от
центра О до точки приложения силы
(F=-cr),
где с —
постоянный коэф., численно равный силе,
действующей на единице расстояния. К.
с. является силой центральной и
потенциальной с силовой ф-цией U=-0,5cr2.
Примерами К. с. служат силы упругости,
возникающие при малых деформациях
упругих тел (отсюда и сам термин «К.
с.»). Приближённо К. с. можно также
считать касательную составляющую силы
тяжести, действующей на матем. маятник
при малых его отклонениях от вертикали.
Для материальной точки, находящейся
под действием К. с., центр О является
положением её устойчивого равновесия.
Выведенная из этого положения точка
будет в зависимости от нач. условий или
совершать около О прямолинейные гармонич.
колебания, или описывать эллипс (в
частности, окружность).
Линейное
неоднородное дифференциальное уравнение:
(147.5)
Применяем
впоследствии его решение для вынужденных
колебаний конкретной физической природы
(x0 в
случае механических колебаний
равно F0/m, в
случае электромагнитных — Um/L).
Решение
уравнения равно сумме общего решения
(146.5)
однородного уравнения
и
частного решения неоднородного уравнения.
Частное решение найдем в комплексной
форме. Заменим правую часть уравнения
(147.5) на комплексную величину х0
:
(147.6). Частное
решение этого уравнения будем искать
в виде
Подставляя
выражение для s и
его производных 
в
уравнение (147.6), получаем
(147.7). Так как это
равенство должно быть справедливым для
всех моментов времени, то время t из
него должно исключаться. Отсюда следует,
что h=w. Учитывая
это, из уравнения (147.7) найдем величину s0 и
умножим ее числитель и знаменатель на 
.
Это комплексное число удобно представить
в экспоненциальной форме:
,
где
(147.8);
(147.9)
Следовательно,
решение уравнения (147.6) в комплексной
форме примет вид
Его
вещественная часть, являющаяся решением
уравнения (147.5), равна
(147.10)
где А и j задаются
соответственно формулами (147.8) и (147.9).
Таким
образом, частное решение неоднородного
уравнения (147.5) имеет вид
(147.11). Решение
уравнения (147.5) равно сумме общего решения
однородного уравнения
(147.12). (см. (146.5)) и частного решения
(147.11). Слагаемое (147.12) играет существенную
роль только в начальной стадии процесса
(при установлении колебаний) до тех пор,
пока амплитуда вынужденных колебаний
не достигнет значения, определяемого
равенством (147.8). Графически вынужденные
колебания представлены на рис. 209.
Следовательно, в установившемся режиме
вынужденные колебания происходят с
частотой w и
являются гармоническими; амплитуда и
фаза колебаний, определяемые выражениями
(147.8) и (147.9), также зависят от w.
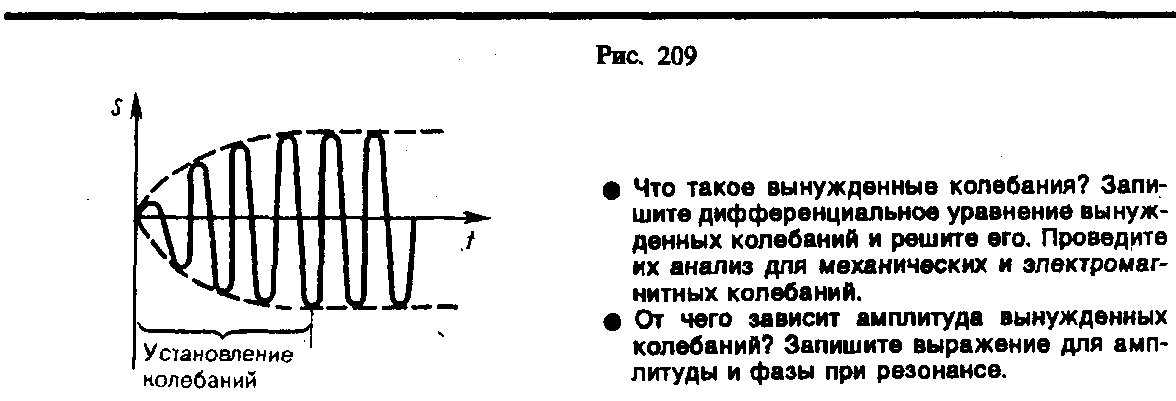
Выведите
формулу для расчета периода: используем
соотношение F=-kx (квазиупругая сила) ,
где k — жесткость пружины. В вертикальном
положении на груз на пружине действуют
сила тяжести и сила упругости пружины.
Под действием силы тяжести пружина
растягивается на х1,
а затем мы отклоняем его от этого
положения на х. Тогда согласно второму
закону Ньютона, учитывая знаки проекций,
получим:
.
Но
,
тогда:
.
Или
—
ускорение тела, колеблющегося на пружине,
не зависит от силы тяжести, действующей
на это тело. Сила тяжести только приводит
к изменению положения равновесия.
Выразим
ускорение:
.
Сравним полученное уравнение с уравнением
колебательного движения
.
Видно, что
или
—
циклическая частота при колебаниях
пружинного маятника. Период
колебаний
или
(формула
Гюйгенса).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная
»
Самолетостроение
»
Физика
»
Колебания математического и физического маятника
Колебания математического и физического маятника
Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 
, и момент инерции:
M = FL .
Момент инерции J в данном случае
Угловое ускорение:
С учетом этих величин имеем:
или
 |
(7.8) |
Его решение
,
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
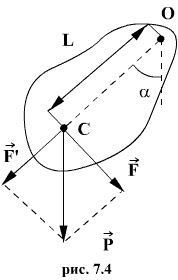
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
 |
(7.10) |
 |
(7.11) |
Решение этого уравнения
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 
или
.
Из этого соотношения определяем
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Чему равна первоначальная длина математического маятника, если при увеличении его длины на 30 см период колебания маятника увеличивается в 2 раза?
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Механические колебания. Номер №1803
Решение
Дано:
△l = 30 см;
T
2
=
2
T
1
.
Найти:
l
1
− ?
СИ:
△l = 0,3 м.
Решение:
△
l
=
l
2
−
l
1
=
0
,
3
м;
l
2
=
l
1
+
0
,
3
;
Период колебания математического маятника равен:
T
=
2
π
l
g
;
Т.к.
T
2
=
2
T
1
,
l
2
=
l
1
+
0
,
3
, то уравнение примет вид:
2
π
l
2
g
=
2
π
l
1
+
0
,
3
g
=
2
∗
2
π
l
1
g
;
l
1
+
0
,
3
=
2
∗
l
1
;
Возведём обе части уравнения в квадрат:
l
1
+
0
,
3
=
4
l
1
;
3
l
1
=
0
,
3
;
l
1
=
0
,
3
3
=
0
,
1
м = 10 см.
Ответ: 10 см.
Приведенная длина маятника, формула
Приведенной длиной физического маятника называется длина математического маятника с тем же периодом колебаний.
Если
| l´ | приведенная длина маятника, | метр |
|---|---|---|
| JA | момент инерции тела относительно оси, проходящей через точку подвеса А, | кг · метр2 |
| m | масса физического маятника, | кг |
| s | расстояние от точки подвеса А тела до его центра масс О, | метр |
то в соответствии с формулами Математический маятник [4] и Физический маятник [4]
[
2πsqrt{frac{l´}{g}} = 2πsqrt{frac{J_{A}}{mgs}}
]
или
[
l´ = frac{J_{A}}{ms}
]
Вычислить, найти приведенную длину маятника, по формуле (2)
Приведенная длина маятника |
стр. 548 |
|---|
«Мир,
в котором мы живём,
удивительно
склонен к колебаниям….
Колеблются
даже атомы,
из
которых мы состоим».
Данная
тема посвящена решению задач на математический маятник.
Задача
1.
Математический маятник совершил 30 колебаний за минуту. Найдите период и
частоту колебаний, а также длину маятника.
|
ДАНО: |
СИ |
РЕШЕНИЕ Период колебаний можно определить по формуле Частота колебаний рассчитывается по формуле Период колебаний математического маятника рассчитывается Преобразуем эту формулу и выразим из неё длину маятника |
|
|
Ответ:
период – 2 с, частота – 0,5 Гц, длина маятника – 99 см.
Задача
2.
При уменьшении длины математического маятника на 2 см, период его колебаний
уменьшается в 1,5 раза. Найдите первоначальную длину маятника.
|
ДАНО: |
СИ |
РЕШЕНИЕ Период колебаний математического маятника определяется по В соответствии с этим, Т.к. период колебаний уменьшился в 1,5 раза, то получаем Преобразуем полученную |
|
|
Ответ:
3,6 см.
Задача
3.
Математический маятник, проходя нижнюю точку имеет скорость 1 м/с, а его
длина равна 20 см. Определите вертикальное отклонение маятника от положения
равновесия в момент времени t = 5 с,
если в начальный момент времени маятник находится на максимальной высоте.
|
ДАНО: |
СИ |
РЕШЕНИЕ Поскольку в начальный момент Запишем уравнение гармонических Исходя из начального Запишем закон сохранения энергии, который выполняется для Тогда Циклическая частота Т.к амплитуда и циклическая То уравнение гармонических А по прошествии 5 с |
|
|
Ответ:
4,5 см.
Задача
4.
Шарик массой 200 г, подвешенный на нити совершает колебания. Шарику сообщили
заряд 300 мкКл и поместили всю систему в электростатическое поле, линии
напряжённости которого направлены вертикально вниз. После этого циклическая
частота колебаний увеличилась вдвое. Найдите напряжённость поля.
|
ДАНО: |
СИ |
РЕШЕНИЕ Циклическая частота Сила тяжести Электростатическая сила В электростатике заряд – это Запишем теперь выражение для Для конечной циклической Т.к. по условию задачи Преобразуем данную формулу и
|
|
|
Ответ:
1960 Н/Кл.
Задача
5.
Материальная точка на нерастяжимой нити длиной 0,3 м совершает колебания,
так что максимальный угол отклонения нити от вертикали составляет 30º.
Найдите положение материальной точки в момент времени t = 5 с
в системе отсчёта, связанной с положением равновесия. В начальный момент
времени точка находится в положении равновесия.
|
ДАНО: |
РЕШЕНИЕ Запишем уравнение Очевидно, что амплитуда Циклическая частота математического Тогда с учётом того, что Уравнения гармонических Тогда координаты точки через |
|
|
Ответ:
(–4,8 см; 1,3 см).