Закон радиоактивного распада. Период полураспада
- Подробности
- Обновлено 20.07.2018 21:25
- Просмотров: 1196
«Физика — 11 класс»
Радиоактивный распад подчиняется статистическому закону.
Резерфорд, исследуя превращения радиоактивных веществ, установил опытным путем, что их активность убывает с течением времени.
Об этом говорилось в предыдущем параграфе.
Так, активность радона убывает в 2 раза уже через 1 мин.
Активность таких элементов, как уран, торий и радий, тоже убывает со временем, но гораздо медленнее.
Для каждого радиоактивного вещества существует определенный интервал времени, на протяжении которого активность убывает в 2 раза.
Этот интервал носит название период полураспада.
Период полураспада (Т) — это время, в течение которого распадается половина начального числа радиоактивных атомов.
Спад активности, т. е. числа распадов в секунду, в зависимости от времени для одного из радиоактивных препаратов изображен на рисунке.
Период полураспада этого вещества равен 5 сут.
Пусть число радиоактивных атомов в начальный момент времени (t = 0) равно N0.
Тогда по истечении периода полураспада это число будет равно
Спустя еще один такой же интервал времени это число станет равным:
По истечении времени t = nТ, т. е. спустя n периодов полураспада Т, радиоактивных атомов останется:
Поскольку
то
Это и есть основной закон радиоактивного распада.
По формуле можно найти число нераспавшихся ядер в любой момент времени.
Период полураспада — основная величина, определяющая скорость радиоактивного распада.
Чем меньше период полураспада, тем меньше времени «живут» ядра, тем быстрее происходит распад.
Для разных веществ период полураспада имеет сильно различающиеся значения.
Так, период полураспада урана 
Именно поэтому активность урана на протяжении нескольких лет заметно не меняется.
Период полураспада радия значительно меньше — он равен 1600 лет.
Поэтому активность радия значительно больше активности урана.
Есть радиоактивные элементы с периодом полураспада в миллионные доли секунды.
Чтобы определить период полураспада, надо знать число атомов N0 в начальный момент времени и число нераспавшихся атомов N спустя определенный интервал времени t.
Сам закон радиоактивного распада довольно прост.
Но физический смысл этого закона уяснить себе нелегко.
Действительно, согласно этому закону за любой интервал времени распадается одна и та же доля имеющихся атомов (за период полураспада половина атомов).
Значит, с течением времени скорость распада нисколько не меняется?
Радиоактивные ядра «не стареют»..
Так, ядра радона, возникающие при распаде радия, претерпевают радиоактивный распад как сразу же после своего образования, так и спустя 10 мин после этого.
Распад любого атомного ядра — это, так сказать, не «смерть от старости», а «несчастный случай» в его жизни.
Для радиоактивных ядер не существует понятия возраста.
Можно определить лишь их среднее время жизни τ.
Время существования отдельных ядер может варьироваться от долей секунды до миллиардов лет.
Атом урана, например, может спокойно пролежать в земле миллиарды лет и внезапно взорваться, тогда как его соседи благополучно продолжают оставаться в прежнем состоянии. Среднее время жизни τ — это просто среднее арифметическое времени жизни достаточно большого количества атомов данного вида.
Оно прямо пропорционально периоду полураспада.
Предсказать, когда произойдет распад ядра данного атома, невозможно.
Смысл имеют только утверждения о поведении в среднем большой совокупности атомов.
Закон радиоактивного распада определяет среднее число ядер атомов, распадающихся за определенный интервал времени.
Но всегда имеются неизбежные отклонения от среднего значения, и, чем меньше количество радиоактивных ядер в препарате, тем больше эти отклонения.
Закон радиоактивного распада является статистическим законом.
Говорить об определенном законе радиоактивного распада для малого числа ядер атомов не имеет смысла.
Этот закон справедлив в основном для большого количества частиц.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Физика атомного ядра. Физика, учебник для 11 класса — Класс!ная физика
Методы наблюдения и регистрации элементарных частиц —
Открытие радиоактивности. Альфа-, бета- и гамма-излучения —
Радиоактивные превращения —
Закон радиоактивного распада. Период полураспада —
Открытие нейтрона —
Строение атомного ядра. Ядерные силы. Изотопы —
Энергия связи атомных ядер —
Ядерные реакции —
Деление ядер урана —
Цепные ядерные реакции —
Ядерный реактор —
Термоядерные реакции. Применение ядерной энергии —
Получение радиоактивных изотопов и их применение —
Биологическое действие радиоактивных излучений —
Краткие итоги главы —
Три этапа в развитии физики элементарных частиц —
Открытие позитрона. Античастицы
stanislav MM, период полураспада — термин, который относится к спонтанному распаду. Он равен времени, в течении которого, количество распадающихся ядер данного изотопа уменьшается вдвое. Поскольку такой распад, — процесс вероятностный и произвольный, зависимость количества ядер от времени — функция, только от времени, так как вероятность распада одного ядра данного изотопа, — величина постоянная. Разумеется точность данной зависимости тем выше, чем больше ядер в описываемой системе. Сама функция — экспонента, отражает изменение величины, убывание которой пропорционально её количеству и встречается довольно часто. Пример — падение давления от времени в проколотом мяче. Пусть вероятность того, что за единицу времени данное ядро распадётся, равна λ (величина обратная его среднему времени жизни) тогда для N ядер для малого времени dt скорость изменения количества:
значение С определяем из начального условия N(0)=N0
Для условия для t = T1/2
получим:
где
τ — среднее время жизни ядра данного изотопа.
Единицы радиоактивности
При использовании радиоизотопов важно знать не только их массу, но и скорость распада, так как именно она определяет количество излучаемых частиц на единицу массы, и именно эти частицы нужно обнаружить.
Скорость распада (Rb) радиоизотопа можно выразить следующим образом:
Rb = 0,693?N/T, (Уравнение 10.6)
где N — общее количество радиоактивных атомов; Т — период полураспада в секундах.
Возьмем грамм радия. Массовое число самого долгоживущего изотопа радия (его в большинстве случаев и называют «радием») равно 226. Это означает, что в 226 граммах радия содержится число Авогадро, т. е. 6,023?1028 атомов (см. гл. I). Таким образом, количество атомов в одном грамме радия равняется числу Авогадро, разделенному на 226, или 2,66?102‘. Период полураспада радия-226 — 1620 лет, или 5,11?1010 секунд.
Подставив в формулу 10.6 N= 2,66?1021, а вместо Т — 5,11?1010, получаем = 3,6?1010. Это значит, что в грамме радия каждую секунду распадается 36 000 000 000 атомов.
В 1910 году единица, обозначающая количество атомов, распадающихся в одном грамме радия за одну секунду, получила название кюри, в честь первооткрывателей радия. К тому времени были проведены более точные расчеты, в ходе которых выяснилось, что за секунду в грамме радия распадается 37 000 000 000 атомов.
Таким образом, за 1 кюри принят распад 3,7?1010 атомов в секунду. Количество распадов в одном грамме радиоизотопа является его удельной радиоактивностью. Удельная радиоактивность атома радия равняется 1 кюри на грамм.
А как быть с другими изотопами? Скорость распада обратно пропорциональна периоду полураспада. Чем дольше период полураспада, тем меньше атомов распадается за одну секунду в данном количестве вещества, и наоборот. Получается, что скорость полураспада пропорциональна Tr/Ti где Tr — период полураспада радия–226, а Ti — период полураспада данного изотопа.
При фиксированной скорости полураспада количество атомов, распадающихся в грамме изотопа, обратно пропорционально массовому числу изотопа. Если изотоп тяжелее радия–226, то в одном его грамме содержится меньше атомов, и количество распадающихся в одном грамме атомов также будет меньше. Количество распадающихся атомов пропорционально Mr/Mi где Mr — массовое число радия–226, а Mi — массовое число данного изотопа.
Удельная радиоактивность (SH) радиоизотопа, т. е. количество распадающихся атомов в одном грамме за одну секунду, по сравнению с одним граммом радия, зависит от периодов полураспада и массовых чисел следующим образом:
SH = TrMr/TiMi. (Уравнение 10.7)
Так как период полураспада радия–226 равен 5,11?1010 секундам, а его массовое число равно 226, числитель формулы 10.7 равен 226(5,11?1010) = 1,15?1013. Тогда:
SH = 1,15?1013/TiMi. (Уравнение 10.8)
Например, для углерода–14, с периодом полураспада 5770 лет, или 1,82?10– секунд, и массовым числом 14, значение TiMi равно 2,55?1012. Разделив 1,15?1013 на 2,55?1012, получаем, что удельная радиоактивность углерода–14 равна 4,5 кюри на грамм. Период полураспада углерода–14 длине равен периода полураспада радия–226, соответственно скорость его распада ниже. С другой стороны, углерод–14 гораздо легче радия–226, значит, в одном грамме углерода–14 распадается больше атомов, и фактическое количество распадающихся атомов в одном грамме углерода–14 выше, чем в одном грамме радия–226, несмотря на более низкую скорость распада.
В целом у большинства используемых в лаборатории радиоизотопов периоды полураспада короче, а массовые числа меньше, чем у радия, поэтому удельная радиоактивность, как правило, очень высока.
Так, например, период полураспада углерода–11 20,5 минуты, или 1230 секунд, массовое число — 11 и удельная радиоактивность — 850 000 000 кюри на грамм.
Впрочем, эти радиоизотопы никогда не используются в граммах. Во-первых, такое их количество просто невозможно получить, а во-вторых, если даже это было бы возможно, оно слишком опасно. Кроме того, большие количества просто не нужны. При точном обнаружении частиц удобно использовать гораздо меньшие, чем 1 кюри, единицы, например милликюри (1/1000 кюри) и микрокюри 1/1000000 кюри). Один микрограмм углерода–11 равноценен 850 микрокюри.
Даже один микрокюри означает распад 36 000 атомов в секунду. На практике удается зафиксировать в лучшем случае распад четырех атомов в секунду, то есть 1/9000 кюри, или 1,1?1010 кюри.
В какой-то мере пользоваться кюри неудобно из-за того, что эта единица отражает распад большого и «нечетного» количества атомов в секунду. Поэтому была введена новая единица — резерфорд (названная так в честь создателя ядерной модели атома). Один резерфорл — это распад миллиона атомов в секунду.
Таким образом, в 1 кюри — 37 000 резерфордов, а в 1 резерфорде — 270 микрокюри.
4. Решение задач
Задача 1. Определите период полураспада радона, если за 1 сутки из 106 ядер распадается 175000 штук.
Решение. При решении задачи используем закон радиоактивного распада: 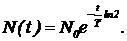
Из него следует 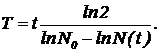
Через сутки останется N(t)=106 –0,175×106=0,825×106. Подстановка дает×
Задача 2. Период полураспада одного из изотопов йода составляет 8 суток. Через какое время число атомов этого изотопа уменьшится в 100 раз?
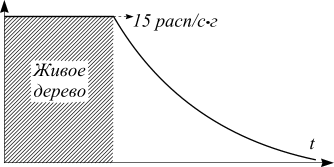
, усвоенного деревом при его росте, остается постоянной величиной вплоть до его гибели. В погибшем дереве содержание начинает уменьшаться вследствие b—распада. Определите возраст деревянного предмета, обнаруженного при археологических раскопках, если активность, приходящаяся на единицу массы вещества, составляет 0,1 удельной активности свежесрубленного дерева. Период полураспада изотопа
равен 5730 годам.
Решение. Задача поясняет метод радиоуглеродного определения возраста археологических находок и возраста различных осадочных пород. Перед началом решения ознакомимся с идеей метода.
Нейтроны, содержащиеся в космических лучах, налетают на атомы азота атмосферы, которые могут превращаться в атомы углерода по схеме (10)
Изотоп углерода является радиоактивным с периодом полураспада 5730 лет. Образующиеся в верхних слоях атмосферы изотопы
перемешиваются с воздухом, окисляются до CO2. При постоянном потоке космических лучей устанавливается динамическое равновесие между подпиткой атмосферы вновь рождающимися атомами радиоактивного углерода и убылью за счет распадов. Растения усваивают углерод в виде углекислого газа, и отношение скорости усвоения с радиоактивным изотопом к скорости усвоения обычного CO2 остается постоянной. Так что радиоактивный углерод, участвующий в жизненных циклах растений и животных, имеет строго определенную концентрацию. При установившемся значении концентрации активность равна, примерно, 15 распадам на один грамм углерода в секунду органического происхождения. Это активность живого растения. Определяя активность углерода органического происхождения после гибели растения, можно определить время, прошедшее после гибели.
Следуя идее решения предыдущей задачи, имеем
Задача 4. Определить период полураспада радия, если известно, что кусочек радия массой 1 г выбрасывает 3,7×1010 a-частиц за одну секунду.
Задача 5. Определите число распадных электронов, испускаемых 1 кг изотопа фосфора за одни сутки. Период полураспада изотопа равен 14 суткам.
5. Домашнее задание
5.2 Решение задач
Задача 1. В периодической системе элементов рядом расположены три элемента. Условно назовем их a, b, c. Радиоактивный изотоп элемента a превращается в изотоп элемента b, а тот, в свою очередь, — в изотоп элемента c. Последний превращается в изотоп исходного элемента a. Какими процессами обусловлены эти превращения?
Задача 2. В микрокалориметр с теплоемкостью 1000 Дж/К помещено 100 мг изотопа кобальта (атомная масса 61). При распаде одного ядра кобальта выделяется энергия 2×10-19 Дж. Через 50 мин температура калориметра повысилась на 0,06 К. Пренебрегая тепловыми потерями, найдите период полураспада изотопа кобальта.
Задача 3. При распаде урана-238 массой 1 кг излучается 1,24×107 a-частиц за одну секунду. Определите период полураспада этого изотопа.
занятие 2.2.4
измерение радиоактивности
1. Обсуждение домашнего задания
2. Решение задач
Задача 1. В цепочке радиоактивных превращений элемента с порядковым номером 92 и атомной массой 235 в элемент порядковым номером 82 и атомной массой 207 (уран-235 в свинец-207) имеется несколько a-распадов и b-распадов. Сколько всего распадов в этой цепочке?
Решение. Пусть произошло n этапов a-распадов и k этапов b-распадов. Из закона сохранения заряда, следует
92-2n+k=82
Из закона сохранения барионного заряда —
235-4n=207
Совместное решение системы дает: k=4; n=7. Всего одиннадцать звеньев в цепочке распадов.
Задача 2. Изотоп плутония a-радиоактивен. Процесс его распада идет следующим образом:
При этом распаде освобождается энергия, большая часть которой идет на кинетическую энергию a-частиц. Однако часть энергии оказывается в ядре урана, которое сбрасывает ее, испуская фотон. Определите скорость вылета a-частиц, если фотон уносит 0,09 МэВ. Массы ядер, участвующих в реакции, в углеродных единицах следующие:
mPu=239,05122 а. е.м., mU=235,04299 а. е.м., mHe=4,00260 а. е.м.
Решение. Разность дефектов масс левой и правой частей реакции равна
DM=239,05122-235,04299-4,00269=0,00563 (а. е.м.)
Энергетический выход реакции
Eвых=DMc2 (Дж) или DM×931,5 (МэВ)=5,24 МэВ.
Энергия a-частицы
Ea=Eвых-Eg=5,24-0,09=5,15 МэВ=8,24×10-13 Дж.
Скорость a-частицы — 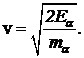
Подстановка дает v»1.6×107 м/с, что составляет примерно 0,05 с. Частица нерелятивистская.
Задача 3. Азот облучается в течение одного часа пучком a-частиц. Найдите количество атомов образовавшегося изотопа
, если ток в пучке 2×10-4А и ядерную реакцию превращения азота в кислород вызывает одна частица из каждых ста тысяч в пучке.
3. Измерение радиоактивности
3.1 Определение и примеры
Радиоактивностью, или просто активностью, называют величину, пропорциональную скорости радиоактивного распада вещества. 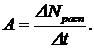
Она измеряется в кюри (Ku) или в резерфордах (Рф):
1 Ku=3,7×1010 расп/с; 1 Рф=106 расп/с. (2)
Задача 4. В свинцовой капсуле находится 4×1018 атомов радия. Определите активность данного количества радия, если период полураспада равен 1620 годам.
Решение. Требуется определить число распадов в одну секунду, а период полураспада — годы, поэтому заведомо выполняется . Так что можно воспользоваться формулой из прошлого занятия:
Задача 5. Имеется урановый препарат с активностью 0,56 mKu. Определите количество изотопа в препарате, если его период полураспада 7,1×108 лет.
Решите задачу для самоконтроля.
Задача 6. В капсуле находится 0,15 моля изотопа плутония . Определите активность данного количества плутония, если его период полураспада равен 2,44×104 лет.