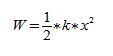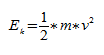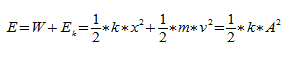Как найти период колебаний бруска

Колебания: интересные задачи

Сложные и средней сложности задачи предлагаю вам в этой статье. Они взяты из задачника Г.А. Никуловой и А.Н. Москалева. После решения этих задач вы будете более уверенно чувствовать себя на ЕГЭ по физике.

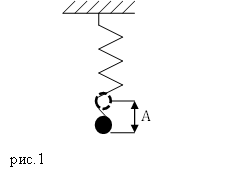
Задача 1.

Найдите период колебаний бруска массой кг в системе, изображенной на рисунке. Жесткость пружин Н/м, Н/м. Трением пренебречь.

На брусок будут действовать две силы упругости: от первой и второй пружин. Причем если одна  пружина растянута, то другая сжата, следовательно, обе силы всегда направлены в одну сторону, так как одна пружина стремится сжаться, а другая, наоборот, растянуться. Таким образом, равнодействующая будет суммой обеих сил:

Тогда общий коэффициент жесткости

Следовательно, период равен

Ответ: с.

Задача 2.

Определите среднюю скорость при колебаниях пружинного маятника с амплитудой см и периодом колебаний с за время движения маятника а) от положения равновесия до отклонения в 0,5 см; б) от максимального отклонения до отклонения 0,5 см.

Средняя скорость – это весь пройденный телом путь, деленный на все время. Определим и то, и другое. Общая форма записи координаты при колебательном движении

Где — начальная фаза. Предположим, она равна нулю – для нашей задачи это совершенно неважно. Тогда, если тело прошло пол-амплитуды, то

Отсюда следует, что

А . Это составляет двенадцатую часть периода:

Теперь можно определять среднюю скорость: разделим путь на время.

Теперь второй случай. Теперь грузик перемещается от точки с максимальной амплитудой до отклонения 0,5 см. Но  если положение равновесия он проходит с максимальной скоростью, и на последующие за положением равновесия 0,5 см у него уходит одно время, то на путь из точки с максимальной амплитудой до 0,5 см у него уйдет больше времени: ведь в точке с максимальной амплитудой он неподвижен.  Определим, сколько понадобится на тот же путь времени в этот раз.  Движение из точки в точку занимает , а движение из точки в точку — время , уже определенное нами ранее. Тогда

Тогда средняя скорость равна

Ответ: 0,06 и 0,03 м/с.

Задача 3.

Груз массой  колеблется на пружине жесткостью с амплитудой . Найдите в точке с координатой : а) кинетическую энергию; б) скорость прохождения грузом этой точки.

Общая форма записи координаты при колебательном движении

Где — начальная фаза. Предположим, она равна нулю. Тогда

Максимальная потенциальная энергия пружины равна

Потенциальная энергия пружины в точке

Тогда кинетическая энергия груза будет равна разности этих потенциальных энергий:

Так как

То скорость в этой точке

Ответ: , .

Задача 4.

Какова частота собственных колебаний соснового бруска массой кг и площадью поперечного сечения см, плавающего в вертикальном положении в озере? Плотность древесины кг/м.

Брусок плавает в озере, сила Архимеда уравновешивает силу тяжести.

Если мы чуть надавим и погрузим брусок чуть больше, то возникнет добавка к уже ранее погруженной части, дополнительный погруженный объем, и «излишек» силы Архимеда, который и станет возвращающей силой и вызовет колебания бруска, когда мы его отпустим.

Этот «излишек» Архимедовой силы равен

Где — дополнительная глубина, на которую мы погрузили брусок.

Эту силу можно считать «силой упругости воды», и записать так:

Тогда «коэффициент упругости воды» будет равен

Частота колебаний определяется формулой

Ответ: 1,76 Гц.

Задача 5.

Найдите период колебаний математического маятника длиной см, подвешенного в вагоне, движущемся горизонтально с ускорением м/с.

На маятник будет воздействовать ускорение, являющееся суммой и :

Период колебаний такого маятника равен

Линия отвеса тоже поменяет положение, отклонившись от вертикали на угол:

Ответ: с, .

Задача 6.

С каким ускорением и в каком направлении должна двигаться кабина лифта, чтобы находящийся в ней  секундный маятник за время мин с совершил колебаний?

Период колебаний математического маятника определяется формулой:

Период был равен 1 с, а потом под действием ускорения изменился, и стал равен

Так как длина нити не менялась, а период вырос в полтора раза, следовательно, изменилось ускорение: ускорение свободного падения уменьшилось на величину ускорения лифта. Из этого делаем вывод, что лифт идет вниз.

Длину нити найдем из условия, что истинный период маятника – секунда:

И подставим:

Ответ: 5,6 м/с.

Задача 7.

Определите период колебаний маятника. Масса груза 400 г, жесткость пружины Н/м. Массой стержня пренебречь. Точка прикрепления пружины к стержню делит ее длину в отношении , считая от шарика. В положении равновесия стержень горизонтален, а ось пружины вертикальна.

По правилу моментов запишем

Где — сила, растягивающая пружину.

Тогда растяжение пружины

Если таково растяжение пружины, то «ход» груза на конце стержня будет в 1,5 раза больше – из подобия треугольников. Тогда

То есть эквивалентная масса груза ()

Следовательно, период колебаний

Ответ: 1,88 с

Содержание книги

Предыдующая страница

§17. Механические колебания

17.3 Простейшие колебательные системы.

Если система обладает одной степенью свободы и в ней возможны гармонические колебания, то такая система называется гармоническим осциллятором^[1]. Рассмотрим несколько примеров таких механических систем, которые также называют маятниками.

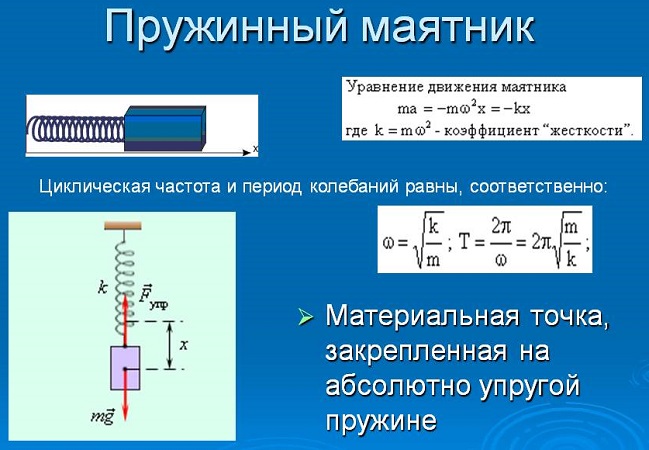
17.3.1 Пружинный маятник.

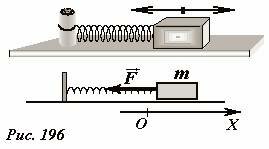
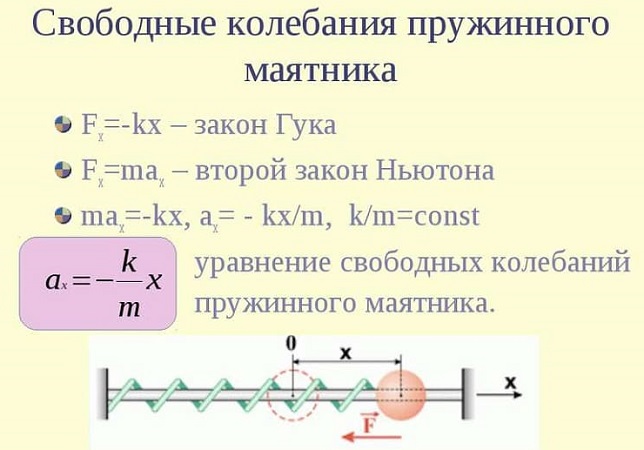
Рассмотрим движение небольшого бруска массой m, расположенного на гладкой горизонтальной поверхности и прикрепленного к неподвижному упору с помощью легкой пружины жесткости k (Рис. 196). Положение бруска будем описывать с помощью декартовой координаты x, начало отсчета которой совместим с положением, в котором пружина не деформирована. При отклонении бруска от положения равновесия на него будет действовать сила упругости пружины (~vec F), направленная к положению равновесия, ее модуль определяется законом Гука (F = kx). На основании второго закона Ньютона и, пренебрегая трением, запишем уравнение, описывающее движение бруска

(~ma = -kx) . (1)

Из этого уравнения следует, что ускорение бруска зависит от его координаты

(~a = -frac{k}{m} x) , (2)

то есть пропорционально координате с отрицательным коэффициентом пропорциональности. Сравнивая с полученным ранее кинематическим уравнением, связывающим ускорение тела с его координатой

(~a = -omega^2 x) , (3)

мы убеждаемся в их полной тождественности. На основании этого мы делаем обоснованный вывод: в рассматриваемой системе брусок совершает гармонические колебания (x = A cos (omega t + varphi_0)). Частота этих колебаний не зависит от их амплитуды и легко находится из сравнения уравнений (2) и (3), идентичность которых требует выполнения условия (~omega^2 = frac{k}{m}), или

(~omega = sqrt{frac{k}{m}} ; nu = frac{1}{2pi} sqrt{frac{k}{m}}) . (4)

Период колебаний бруска равен

(~T = frac{2pi}{omega} = 2 pi sqrt{frac{m}{k}}) .

Полученные формулы для частоты и периода колебаний качественно легко объяснимы: частота колебаний возрастает с ростом жесткости пружины и убывает при возрастании массы груза.

Колебания, возникающие под действием внутренних возвращающих консервативных сил, называются свободными.

Подчеркнем, сейчас мы получили уравнение (2) на основании законов динамики, его совпадение с рассмотренным ранее кинематическим уравнением (3) заранее не предполагалось, это можно даже назвать «счастливым совпадением».

Закон движения бруска однозначно определяется при задании начальных условий. Зависимость параметров закона движения от начальных условий была рассмотрена нами ранее, поэтому здесь укажем только два крайних случая начальных условий.

Если мы отклоним брусок от положения равновесия на расстояние A и отпустим его без толчка (начальные условия: при t = 0 x₀ = A, υ₀ = 0), то закон движения будет иметь вид

(~x = A cos omega t) . (5)

В другом предельном случае, когда бруску резким толчком сообщают начальную скорость (начальные условия: при t = 0 x₀ = 0, υ = υ₀), закон движения будет несколько иным

(~x = frac{upsilon_0}{omega} sin omega t) . (6)

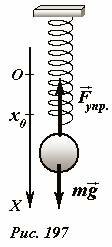
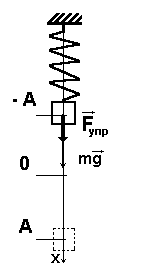
Рассмотрим теперь описание движения небольшого шарика массой m, подвешенного на легкой пружине жесткостью k (Рис. 197). Направим ось Ox вертикально вниз, начало отсчета совместим с положением недеформированной пружины. В процессе движения на шарик действуют сила тяжести (~m vec g) и сила упругости (~vec F_{ynp}), модуль которой определяется законом Гука (F_{ynp} = kx). Уравнение второго закона Ньютона в проекции на введенную ось имеет вид

(~ma = mg — kx) . (7)

Так как сила упругости зависит от координаты шарика (следовательно, не постоянна), то движение шарика не будет равноускоренным. Понятно, что движение шарика будет колебательным, но, на первый взгляд, уравнение его движения (7) отличается от рассмотренного нами уравнения гармонических колебаний – присутствует постоянная составляющая mg. Преобразуем уравнение (7)

(~ma = -k left(x — frac{mg}{k} right)) . (8)

Появившаяся в уравнении величина (~x_0 = frac{mg}{k}) имеет наглядный смысл: она указывает положение равновесия шарика, в котором сила тяжести уравновешивается силой упругости (mg = kx_0). Теперь мы можем сместить начало отсчета оси координат, совместив его с положением равновесия. В этой измененной системе отсчета координата шарика равна (x_1 = x — x_0), ускорение шарика и в новой системе отсчета остается прежним (a_1 = a). Поэтому уравнение движения шарика в этой системе отсчета имеет вид, полностью совпадающий с уравнением гармонических колебаний

(~ma_1 = -kx_1) , (9)

с частотой (~omega = sqrt{frac{k}{m}}). Таким образом, постоянная сила, действующая в колебательной системе, не изменяет частоты колебания, а только смещает положение равновесия. Полное решение уравнения движения (9) нам известно, поэтому можно также записать и полное решение уравнения (7) в исходной системе отсчета

(~x = frac{mg}{k} + A cos omega t + B sin omega t) , (10)

в котором произвольные постоянные A, B определяются из начальных условий.

Еще одним общим методом получения уравнения движения является использование закона сохранения энергии. Рассмотрим превращения энергии в ходе колебаний бруска на гладкой горизонтальной поверхности (Рис. 196). Для того чтобы вывести брусок из положения равновесия к нему необходимо приложить внешнюю силу. Эта сила должна совершить положительную работу, тем самым, сообщая системе энергию. Эта энергия «запасается» в виде потенциальной энергии деформированной пружины и равна (~U_0 = frac{k x^2_0}{2}). Если брусок еще и дополнительно толкнуть, то система получит дополнительную энергию в форме кинетической энергии бруска (~E_{kin0} = frac{m upsilon^2_0}{2}).

В процессе движения бруска происходят постоянные переходы энергии из потенциальной в кинетическую (когда брусок движется к положению равновесия – сила упругости совершает положительную работу, поэтому кинетическая энергия возрастает) и обратно — из кинетической в потенциальную (когда брусок удаляется от положения равновесия – работа силы упругости отрицательна, поэтому кинетическая энергия убывает).

Пренебрегая трением, закон сохранения механической энергии выражается уравнением

(~frac{m upsilon^2}{2} + frac{k x^2}{2} = E) , (11)

в котором сумма кинетической энергии бруска и потенциальной энергии деформированной пружины остается постоянной величиной, которая легко выражается через начальные условия (~E_0 frac{m upsilon^2_0}{2} + frac{k x^2_0}{2}) . В уравнении (11) неизвестной является зависимость координаты от времени x(t), скорость движения является производной от координаты по времени υ(t) = x′(t). Таким образом, с математической точки зрения уравнение (11) содержит неизвестную функцию и ее производную. Подставим в это уравнение закон движения, найденный нами из динамического уравнения (1):

(~x(t) = x_0 cos omega t + frac{upsilon_0}{omega} sin omega t) . (12)

Зависимость скорости от времени описывается в этом случае функцией

(~upsilon(t) = -x_0 omega sin omega t + upsilon_0 cos omega t) . (13)

Не сложно убедится, что эти функции при подстановке в уравнение (11) превращают его в верное тождество (конечно, при (~omega = sqrt{frac{k}{m}})), следовательно, функция (12) является решением этого уравнения.

Таким образом, уравнение (12) также является уравнением гармонических колебаний, оно полностью эквивалентно (равносильно) уравнению (1).

Для доказательства этого утверждения достаточно взять производную по времени от уравнения (11):

(~frac{m}{2} 2 upsilon upsilon’ + frac{k}{2} 2 x x’ = 0) ,

при выводе учтено, что производная от постоянной энергии равна нулю; учитывая, что производная от координаты равна скорости x′ = υ, а производная от координаты есть ускорение υ′ = a, получаем после сокращения уравнение (1) (ma + kx = 0). Можно также провести и обратный математический переход от уравнения (1) к уравнению (11).

Интересно отметить, что решение уравнения (11) можно найти «по теореме Пифагора». Действительно, предположим, что его решением является функция, изменяющаяся по «закону косинуса»; (x(t) = A cos omega t) , тогда скорость будет изменяться «по закону синуса»[upsilon = -omega A sin omega t]. По известному основному тригонометрическому тождеству сумма квадратов синуса и косинуса равна единице, следовательно, можно подобрать такое значение параметра ω, чтобы уравнение (11) приводило к этому тождеству. Подставляя записанные выражения для зависимостей координаты и скорости от времени в уравнение (11), получим

(~frac{m}{2} (-omega A sin omega t)^2 + frac{k}{2} (A cos omega t)^2 = E) ,

после очевидного преобразования

(~frac{kA^2}{2} left(cos^2 omega t + frac{m omega^2}{k} sin^2 omega t right) = E) .

Чтобы это уравнение превратилось в тождество необходимо, чтобы выполнялось условие (~frac{m omega^2}{k} = 1) , из которого следует известная формула для периода колебаний. Амплитуда колебаний A выражается через полную энергию системы.

Подведем основной итог: если на основании физических законов (главным образом закона сохранения энергии) удалось показать, что некоторая переменная величина X(t) и ее производная V(t) = X′(t) связаны соотношением

то величина X изменяется по гармоническому закону, с круговой частотой ω.

17.3.2 Математический маятник.

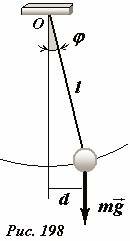
Небольшой шарик, подвешенный на легкой нерастяжимой нити, способен совершать свободное колебательное движение (Рис. 198). Для описания движения маятника будем считать шарик материальной точкой, пренебрежем массой нити и сопротивлением воздуха. Такая модель называется математическим маятником.

В качестве координаты, описывающей положение шарика, выберем угол отклонения нити от вертикали φ. Для описания изменения этой координаты удобно использовать уравнение динамики вращательного движения

(~J varepsilon = M) , (1)

где (J = ml^2) — момент инерции системы, (~varepsilon = frac{Delta omega}{Delta t}) — угловое ускорение тела (вторая производная от угла поворота), M — суммарный момент внешних сил действующих на систему^[2]. На шарик действуют силы тяжести mg и натяжения нити. Момент силы натяжения нити относительно точки подвеса равен нулю, поэтому уравнение (1) для подвешенного шарика приобретает вид

(~ml^2 varepsilon = -mgl sin varphi) , (2)

или

(~varepsilon = -frac{g}{l} sin varphi) . (3)

Это уравнение описывает колебания маятника, но не является уравнением гармонических колебаний, так как момент сил пропорционален синусу угла отклонения, а не самому углу. Однако, если считать углы отклонения малыми (сколько это – мы выясним позднее), можно воспользоваться приближенной формулой (sin varphi approx varphi) в этом приближении уравнение (3) превращается в знакомое уравнение гармонических колебаний

(~varepsilon = -Omega^2 sin varphi) , (4)

где (~Omega = sqrt{frac{g}{l}}) — круговая частота малых колебаний маятника^[3]. Решение этого уравнения мы уже выписывали

(~varphi = varphi_0 cos Omega t) , (5)

здесь φ₀ — максимальное отклонение нити, то есть амплитуда колебаний. Для простоты будем считать, что начальная скорость шарика равна нулю.

Период малых колебаний маятника выражается через круговую частоту

(~T = frac{2 pi}{Omega} = 2 pi sqrt{frac{l}{g}}) . (6)

Так как малые колебания математического маятника являются гармоническими, то их период не зависят от амплитуды. Этот факт был экспериментально отмечен еще Г. Галилеем. При больших углах отклонения период колебаний математического маятника незначительно возрастает.

Отметим, что период колебаний математического маятника не зависит также от массы шарика – вспомните, ускорение свободного падения, а также другие характеристики движения тела в поле тяжести Земли также не зависят от массы тела (если, конечно, пренебрегать сопротивлением воздуха). Формула (6) может быть использована и используется для экспериментального определения ускорения свободного падения. Длина нити и период колебаний достаточно просто измерить экспериментально, затем с помощью формулы (6) можно рассчитать ускорение свободного падения.

Попробуем описать движение математического маятника с помощью закона сохранения механической энергии. Кинетическая энергия шарика выражается формулой (~E_{kin} = frac{J omega^2}{2} = frac{m l^2 omega^2}{2}). Нулевой уровень отсчета потенциальной энергии совместим с точкой подвеса нити, тогда потенциальная энергия шарика равна (U = −mgl cos varphi). Уравнения закона сохранения механической энергии (с учетом начальных условий) имеет вид

(~frac{m l^2 omega^2}{2} — mgl cos varphi = -mgl cos varphi_0) . (7)

Это уравнение также не является уравнением гармонических колебаний. Но, если мы опять будем считать углы отклонения маятника малыми и воспользуемся приближенной формулой (~cos varphi approx 1 — frac{varphi^2}{2}), то уравнение (7) перейдет в уравнение гармонических колебаний

(~frac{m l^2 omega^2}{2} + frac{mgl varphi^2}{2} = frac{mgl varphi^2_0}{2}) ,

или

(~frac{omega^2}{2} + frac{Omega^2 varphi^2}{2} = frac{Omega^2 varphi^2_0}{2}) , (8)

где обозначено (~Omega = sqrt{frac{g}{l}}) — круговая частота колебаний, совпадающая с полученной из динамического уравнения (2).

Конечно, такое совпадение не является случайным – фактически в обоих подходах мы использовали одно и то же приближение малых углов отклонения.

17.3.3 Математический маятник с пружиной.

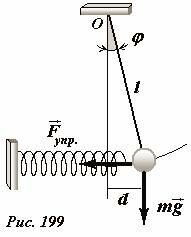
Рассмотрим еще один пример колебательной системы, являющейся «гибридом» математического и пружинного маятника (Рис. 199): к шарику, подвешенному на нити длиной l, прикреплена легкая пружина так, что в положении равновесия нить маятника располагается вертикально (в этом случае пружина не деформирована). По-прежнему, положение маятника будем описывать с помощью угла отклонения φ, который будем считать малым. Уравнение динамики вращательного движения относительно точки подвеса для шарика будет иметь вид

(~J varepsilon = — mgl sin varphi — F_{ynp} l cos varphi) , (1)

где (J = ml^2) — момент инерции маятника, ε — угловое ускорение, (mgl sin varphi) — момент силы тяжести, (F_{ynp} l cos varphi) — момент силы упругости. Считая угол отклонения малым, удлинение пружины можно представить в виде (Delta x = l varphi) и при этом можно считать, что ось пружины все время остается горизонтальной. В этом же приближении можно положить (sin varphi approx varphi) , (cos varphi approx 1). Поэтому уравнение (1) упрощается

(~ml^2 varepsilon = — mgl varphi — kl varphi cdot l) ,

или

(~varepsilon = -left(frac{g}{l} + frac{k}{m} right) varphi) . (2)

Это уравнение является уравнением гармонических колебаний: ускорение пропорционально смещения от положения равновесия. Круговая частота этих колебаний равна

(~Omega = -sqrt{frac{g}{l} + frac{k}{m}}) . (3)

17.3.4 Колебание жидкости в трубке.

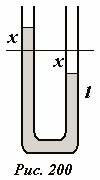
Рассмотрим еще один пример колебательной системы. Пусть в вертикальной U-образной трубке находится вода (Рис. 200). В состоянии равновесия верхний уровень воды расположен на высоте l. Воду вывели из положения равновесия и она совершать колебания, переливаясь из одного колена трубки в другое. Для определения частоты (или периода) этих колебаний воспользуемся законом сохранения энергии. В качестве координаты, характеризующей положение воды, выберем величину x — отклонение уровня воды в одном колене от положения равновесия. Если площадь поперечного сечения трубки S постоянна по ее длине, то скорость течения жидкости будет одинакова и равна производной от введенной координаты (~upsilon = frac{Delta x}{Delta t}). Следовательно, кинетическая энергия движущейся жидкости равна

(~E_{kin} = frac{m upsilon^2}{2} = 2rho Sl frac{upsilon^2}{2}) , (1)

где ρ — плотность воды, 2Sl — ее объем (пренебрегая жидкостью, находящейся в нижней части трубки, которую будем считать малой). Для расчета потенциальной энергии, вспомним, что потенциальная энергия тела в поле тяжести земли равна произведению массы тела, ускорения свободного падения и высоты центра масс, поэтому в рассматриваемом случае

(~U = rho g S (l+x) frac{l+x}{2} + rho g S (l-x) frac{l-x}{2} = rho g S (l^2 + x^2)) , (2)

где первое слагаемое равно потенциальной энергии жидкости в левом колене трубки, второе – в правом. Если пренебречь неизбежными потерями механической энергии из-за сил вязкого трения, то сумма кинетической и потенциальной энергии жидкости постоянна, поэтому

(~rho Sl upsilon^2 + rho g S (l^2 + x^2) = operatorname{const}) .

Из этого уравнения следует, что движение жидкости подчиняется уравнению гармонических колебаний

(~upsilon^2 + frac{g}{l} x^2 = operatorname{const}) , (3)

с круговой частотой (~omega = sqrt{frac{g}{l}}) и периодом (~T = 2 pi sqrt{frac{l}{g}}).

Отметим, что описать движение жидкости на основании уравнений динамики в данном случае сложнее.

Примечания

1. ↑ В переводе с латинского – осцилляции означают колебания.
2. ↑ В принципе, можно использовать и уравнения динамики поступательного движения, но используемый здесь подход является предпочтительным, так как траекторией движения точки является дуга окружности.
3. ↑ Мы выбрали обозначение Ω (это тоже «омега», только заглавная) для собственной частоты малых колебаний, чтобы традиционное обозначение ω — оставить за угловой скоростью движения шарика, которая далее будет фигурировать в наших рассуждениях.

Следующая страница

Механические колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

(2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

.

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

.

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

.

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

. (4)

Теперь дифференцируем полученное равенство (4):

. (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

. (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

. (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

к оглавлению ▴

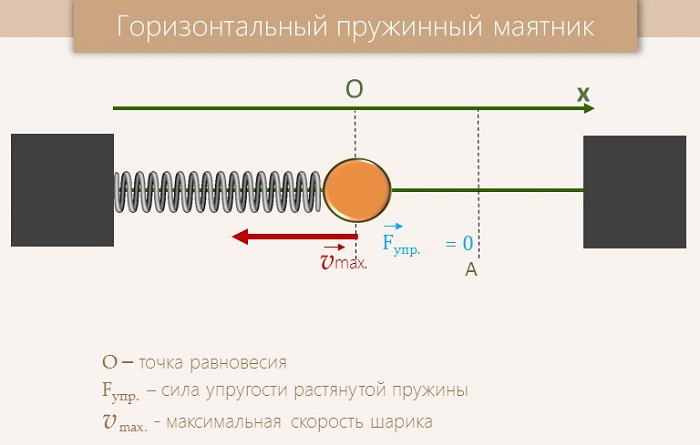
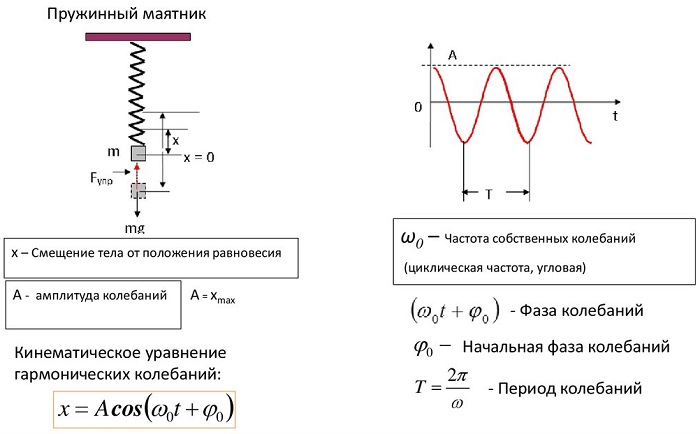
Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

. (8)

Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

или

.

Мы получили уравнение гармонических колебаний вида (6), в котором

.

Циклическая частота колебаний пружинного маятника, таким образом, равна:

. (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

. (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

,

и спроектируем его на ось :

.

Если маятник занимает положение как на рисунке (т. е. ), то:

.

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

.

Итак, при любом положении маятника имеем:

. (11)

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

,

или

.

Это — уравнение гармонических колебаний вида (6), в котором

.

Следовательно, циклическая частота колебаний математического маятника равна:

. (12)

Отсюда период колебаний математического маятника:

. (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

.

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Пружинный маятник — колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики. 

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости. 

Приняты следующие обозначения:

• m — масса тела;

• k — коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

1. Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

2. У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

3. Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

4. Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

5. От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Виды пружинных маятников

Существует два типа данной системы:

1. Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.

2. Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её. 

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

F_упр = — k*x

где k — коэффициент жесткости пружины (Нм),

x – смещение (м).

Уравнения колебаний пружинного маятника

Свободные колебания пружинного маятника описываются с помощью гармонического закона. 

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = — mw2x(t),

где w — радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

Факторы, от которых зависит частота:

1. Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

2. Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника. 

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Потенциальная энергия:

Кинетическая энергия:

Полная энергия:

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

1. Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

2. В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

3. Влияние силы трения при расчете не учитывают.

Дифференциальное уравнение гармонических колебаний пружинного маятника 

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.

Формулы пружинного маятника в физике

Формулы пружинного маятника

Определение и формулы пружинного маятника

Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

[ddot{x}+{omega }^2_0x=0left(1right),]

где ${щu}^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]

где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

[T=2pi sqrt{frac{m}{k}}left(4right).]

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]

начальная фаза при этом:

[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

[E_p=-frac{dF}{dx}(8)]

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]

Закон сохранения энергии для пружинного маятника запишем как:

[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]

где $dot{x}=v$ — скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Примеры задач с решением

Читать дальше: формулы равноускоренного прямолинейного движения.