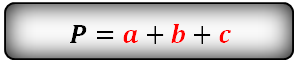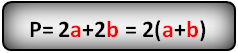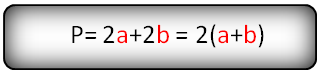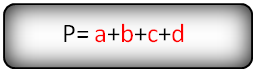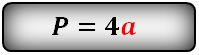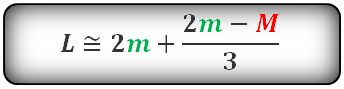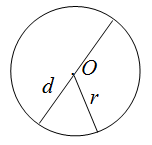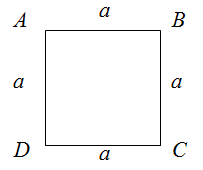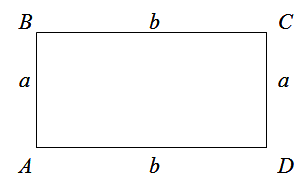Формулы периметра геометрических фигур
Периметром геометрической фигуры
— называют длину границы геометрической фигуры.
Формула периметра треугольника
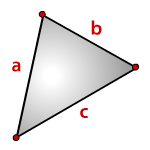
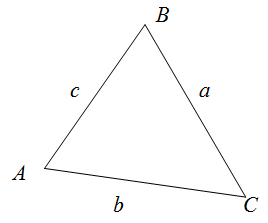
Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
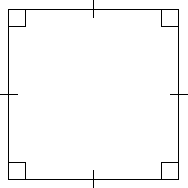
Формулы периметра квадрата
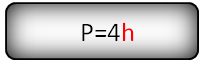
Периметр квадрата равен произведению длины его стороны на четыре.
P = 4a
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
P = 2√2 d
где P — периметр квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Формула периметра прямоугольника
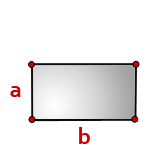
Периметр прямоугольника ABCD равен удвоенной сумме сторон, прилежащих к одному углу.
P = 2(a + b)
где P — периметр прямоугольника,
a, b — длины сторон прямоугольника.
Формула периметра параллелограмма
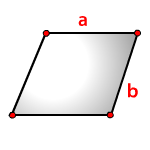
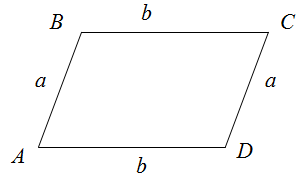
Периметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу
P = 2(a + b)
где P — периметр параллелограмма,
a, b — длины сторон параллелограмма.
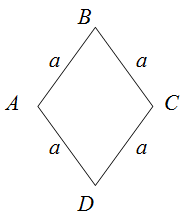
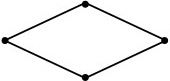
Формула периметра ромба
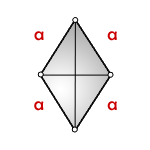
Периметр ромба равен произведению длины его стороны на четыре.
P = 4a
где P — периметр ромба,
a — длина стороны ромба.
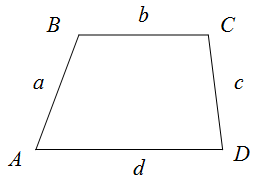
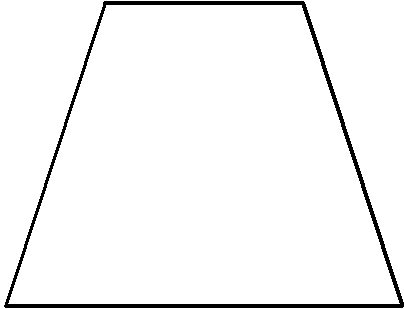
Формула периметра трапеции
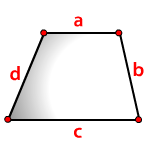
Периметр трапеции равен сумме длин ее сторон.
P = a + b + c + d
где P — периметр трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции.
Формулы длины окружности.
где P — длина окружности,
r — радиус окружности,
d — диаметр окружности,
π = 3.141592.
r — радиус окружности
D — диаметр окружности
π ≈ 3.14
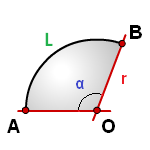
Формула длины окружности, (L):
r— радиус окружности
α— угол AOB, в градусах
π ≈ 3.14
Формула длины дуги (L):
a, b, c, — стороны треугольника
Формула периметра треугольника через его стороны (P):
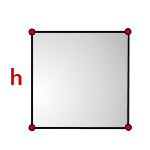
h — сторона квадрата
Формула периметра квадрата, (P):
b — длина прямоугольника
a — ширина прямоугольника
Формула периметра прямоугольника, (P):
a, b — стороны параллелограмма
Формула периметра параллелограмма, (P):
a, b, c,d — стороны трапеции
Формула периметра трапеции, (P):
a — сторона ромба
Формула периметра ромба (P):
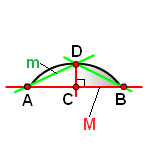
Точка С делит отрезок АВ пополам.
Углы ACD и DCB— прямые, (90°).
m— хорда AD=DB
M— хорда AB
Формула Гюйгенса, длина дуги ADB, (L):
* Погрешность для углов меньше 60°, составляет менее 0,5%
145
Дуга – это часть окружности, отсекаемая хордой. R – радиус окружности α – центральный угол дуги O – центр
123
Окружность – геометрическое место точек, равноудаленных от заданной точки (центра окружности).
123
Окружность – геометрическое место точек, равноудаленных от заданной точки (центра окружности).
3.2к.
Эллипс – это множество точек плоскости, для которых сумма расстояний до фокусов эллипса постоянна и больше
141
Многоугольник – это геометрическая фигура, которая ограничена замкнутой ломаной линией. Правильный многоугольник
441
Шестиугольник – это многоугольник, который имеет шесть углов. Правильный шестиугольник – это выпуклый
348
Пятиугольник – это многоугольник, который имеет пять углов. Правильный пятиугольник – это выпуклый пятиугольник
88
Трапеция – это четырехугольник, у которого параллельна только одна пара противоположных сторон.
90
Квадрат – это параллелограмм, у которого все углы и все стороны равны. а – сторона квадрата A, B, C
66
Ромб – это параллелограмм, у которого все стороны равны. a – сторона ромба A, B, C, D – вершины ромба
Содержание:
- Определения
- Формулы периметра основных геометрических фигур
Определения
Определение
Периметр — общая длина границы фигуры, которая чаще всего находится на плоскости.
Периметр имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Чаще всего этот термин применяется к треугольнику и многоугольникам и в этом случае означает сумму длин всех сторон фигуры.
То есть периметр — это сумма длин сторон какой-либо геометрической фигуры.
Определение
Полупериметр — половина периметра. Употребляется в основном в геометрии треугольника.
Формулы периметра основных геометрических фигур
Периметр треугольника
Чтобы найти периметр треугольника $ABC$,
необходимо сложить длины всех его сторон.
$$P_{Delta A B C}=a+b+c$$
Читать дальше: формула периметра треугольника и примеры решений →
Периметр круга
Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.
Для нахождения длины окружности можно использовать одну из формул
Читать дальше: формула периметра круга и примеры решений →
Периметр квадрата
Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.
$$P_{Delta A B C D}=a+a+a+a=4 a$$
Читать дальше: формула периметра квадрата и примеры решений →
Периметр прямоугольника
Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.
$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$
Читать дальше: формула периметра прямоугольника и примеры решений →
Периметр параллелограмма
Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.
$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$
Читать дальше: формула периметра параллелограмма и примеры решений →
Периметр трапеции
Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.
$$P_{Delta A B C D}=a+b+c+d$$
Читать дальше: формула периметра трапеции и примеры решений →
Периметр ромба
Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.
$$P_{Delta A B C D}=a+a+a+a=4 a$$
Читать дальше: формула периметра ромба и примеры решений →
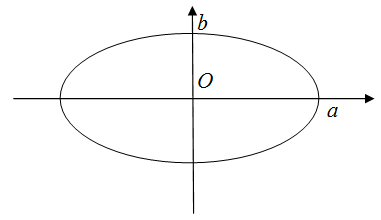
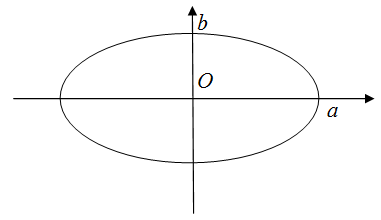
Периметр эллипса
Чтобы найти периметр эллипса
$frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$, нужно воспользоваться формулой
$$P=4 cdot frac{pi a b+(a-b)}{a+b}$$
Читать дальше: формула периметра эллипса и примеры решений →
- Как найти периметр треугольника
- Как найти периметр трапеции
- Как найти периметр ромба
- Как найти периметр эллипса
- Как найти периметр многоугольника
- Как найти периметр прямоугольного треугольника
- Как найти периметр равнобедренного треугольника
- Как найти периметр равностороннего треугольника
- Как найти периметр круга
- Как найти длину окружности
- Как найти периметр квадрата
- Как найти периметр прямоугольника
- Как найти периметр параллелограмма
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Периметр любой геометрической фигур на плоскости определяется как сумма длин всех его сторон. В этой статье, на примере задач, мы приведем формулы для нахождения периметров квадрата, прямоугольника, параллелограмма, трапеции, ромба, многоугольника и эллипса.
Периметр квадрата
Определение 1
Квадратом будем назвать такую геометрическую фигуру, которая состоит из четырех равных сторон, все углы которой прямые (рис. 1).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 1
Найти периметр квадрата, если его сторона равняется $α$.
Решение.
Так как все 4 стороны квадрата равны между собой, то, по определению периметра, получим
$P=α+α+α+α=4α$
Вывод: Для нахождения периметра квадрата надо длину его стоны умножить на $4.$
Периметр прямоугольника
Определение 2
Прямоугольником будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой, все углы которой прямые (рис. 2).
Пример 2
Найти периметр прямоугольника, если его смежные стороны равняются $α$ и $β$.
Решение.
Так как противоположные стороны равняются между собой, то
$P=α+α+β+β=2α+2β=2(α+β)$
«Как найти периметр квадрата, прямоугольника, параллелограмма, трапеции, ромба, эллипса, многоугольника» 👇
Вывод: Для нахождения периметра прямоугольника надо сумму длин его смежных сторон умножить на $2.$
Периметр параллелограмма
Определение 3
Параллелограммом будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой и параллельны друг другу (рис. 3).
Пример 3
Найти периметр параллелограмма, если его смежные стороны равняются $α$ и $β$.
Решение.
Так как противоположные стороны равняются между собой, то
$P=α+α+β+β=2α+2β=2(α+β)$
Вывод: Для нахождения периметра параллелограмма надо сумму длин его смежных сторон умножить на $2.$
Периметр трапеции
Определение 4
Трапецией будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем 2 противоположные стороны, которые называются основаниями, параллельны друг другу (рис. 4).
Пример 4
Найти периметр трапеции, если его стороны равняются $α$, $β$, $γ$ и $δ$.
Решение.
По определению периметра плоской геометрической фигуры получим, что
$P=α+β+γ+δ$
Вывод: Для нахождения периметра трапеции надо сложить все длины его сторон.
Периметр ромба
Определение 5
Ромбом будем назвать такой параллелограмм, у которого все стороны равны между собой (рис. 5).
Пример 5
Найти периметр ромба, если его сторона равняется $α$.
Решение.
Так как все 4 стороны ромба равны между собой, то, по определению периметра, получим
$P=α+α+α+α=4α$
Вывод: Для нахождения периметра ромба надо длину его стоны умножить на $4.$
Периметр многоугольника
Отметим, что все фигуры, рассмотренные выше, являются многоугольниками, а именно четырехугольниками. Поэтому можем рассмотреть более обще понятие, а именно понятие -угольника.
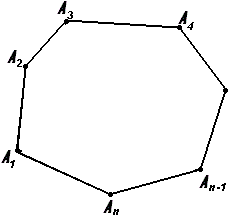
Определение 6
$n$-угольником будем назвать такую геометрическую фигуру, которая состоит из $n$ непересекающихся сторон и $n$ углов. (рис. 6).
Пример 6
Найти периметр $n$-угольника, если его стороны равняются $α_1$, $α_2$,…, $α_n$.
Решение.
По определению периметра плоской геометрической фигуры получим, что
$P=α_1+α_2+⋯+ α_n$
Вывод: Для нахождения периметра -угольника надо сложить все длины его сторон.
Здесь можно выделить периметр правильного $n$-угольника, то есть $n$-угольника, у которого все стороны равняются между собой.
Пример 7
Найти периметр правильного $n$-угольника, если его сторона равняется $α$.
Решение.
Так как все $n$ сторон правильного $n$-угольника равны между собой, то, по определению периметра, получим
$P=α+α+⋯+α+α$ — $n$ раз.
Следовательно
$P=nα$
Вывод: Для нахождения периметра правильного $n$-угольника надо длину его стороны умножить на $n$
Периметр эллипса
Здесь просто введем формулу, для вычисления периметра (или еще иначе длины) эллипса. Пусть нам дан эллипс, как на рисунке 7.
Тогда периметр эллипса равняется
$P=4frac{πab+a-b}{a+b}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме