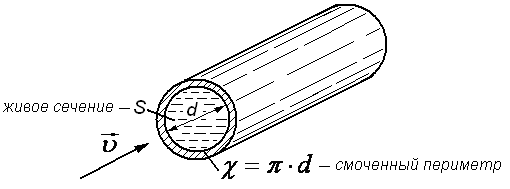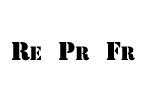В
гидравлических расчётах для характеристики
размеров и формы поперечного сечения
потока вводят понятие о живом
сечении и его элементах: смоченном
периметре и гидравлическом радиусе.
Живым
сечением
называется поверхность в пределах
потока, проведённая нормально к линиям
тока.
Для
круглого трубопровода, когда всё
поперечное сечение заполнено жидкостью,
живым сечение является площадь круга:

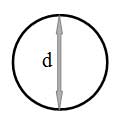
Рис.
3.6. Элементы потока
Смоченным
периметром
называют ту часть периметра живого
сечения, по которой жидкость соприкасается
со стенками трубопровода (рис.3.6).
Смоченный периметр обычно обозначают
греческой
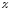
заполненной жидкостью смоченный периметр
равен длине окружности:

Гидравлическим
радиусом
называют отношение живого сечения к
смоченному периметру, т.е. величину

Эта
величина характеризует удельную, т.е.
приходящуюся на единицу длины смоченного
периметра, площадь живого сечения. Легко
сделать вывод, что поток с наибольшим
гидравлическим радиусом при прочих
равных условиях имеет минимальную силу
трения, приложенную к смоченной
поверхности.
Для
круглых труб, полностью заполненных
жидкостью, гидравлический радиус равен
четверти диаметра:

Введение
гидравлического радиуса как характерного
размера позволяет сравнивать по критерию
подобия (Re)
потоки с разными формами живого сечения.
Рассмотренные
основные понятия позволяют решать самые
различные практические задачи гидравлики.
Пример
3.1. Определить
скорость потока в трубопроводе. Диаметр
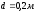
расход воды (несжимаемой жидкости) —
Решение.
Искомая скорость
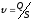
Определим
площадь живого сечения:

Скорость
потока:

3.6. Уравнение количества движения для потока жидкости
Гидравлика
– это техническая механика жидкости,
в которой часто используются упрощённые
методы для решения инженерных задач.
Во многих случаях при решении практических
задач гидравлики удобно применять такие
центральные понятия механики, как
количество движения (уравнение импульсов)
и кинетическая энергия.
В
связи с этим необходимо рассмотреть
возможность вычисления количества
движения и кинетическую энергию потока
жидкости по средней скорости, а не по
действительным местным скоростям. Это
позволит существенно упростить
гидравлические расчёты.
Для
материального тела массой
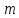
движущегося со скоростью
изменение количества движения за время


где
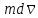
обусловленное импульсом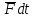
Жидкость
представляет собой материальную систему,
поэтому основной закон механики может
быть приложен к любой выделенной из неё
массе.
Применим
эту теорему механики к участку потока
жидкости с расходом

участок заштрихован). Ограничимся
рассмотрением только установившегося
движения жидкости (рис. 3.7).
За
время

определяемое сечениями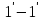

Объёмы этих элементов
а, следовательно, и их массы
движения будет равно

Это
приращение количества движения
обусловлено импульсом всех внешних
сил, действующих на объём жидкости между
сечениями 1-1 и 2-2. Внешними силами,
приложенными к выделенному объёму,
являются сила тяжести всего объёма
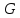
силы давления в первом и втором сечениях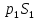

внутрь объёма), а также реакции стенок
трубы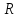
которая складывается из сил давления
и трения, распределённых по боковой
поверхности объёма.
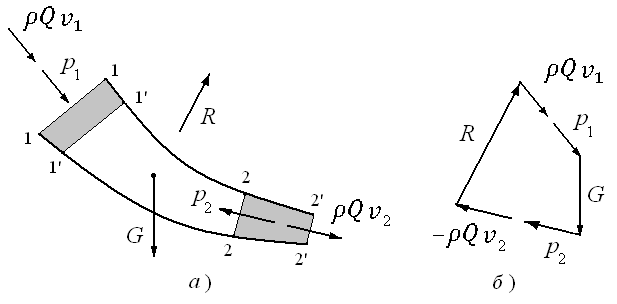
Рис.
3.7. Применение уравнения количества
движения
к
потоку жидкости
Уравнение
импульсов (3.7) для рассматриваемого
случая можно записать в виде
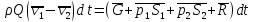
После
сокращения на

Составив
проекции этого векторного уравнения
на три координатные оси, получим три
алгебраических уравнения с тремя
неизвестными —
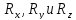
Л.
Эйлер предложил удобный графический
способ нахождения силы

Перенося в формуле (3.?) все слагаемые в
одну сторону, можно представить его в
виде суммы векторов:

0, (3.10)
где
вектор

обратный действительному). В соответствии
с этим выражением (3.10) силу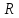
многоугольник сил, как это показано на
рис. 3.7,а.
Анализ
показывает, что при вычислении количества
движения и кинетической энергии по
средней скорости допускается ошибка,
которую можно учесть с помощью двух
коэффициентов:
—
коэффициента Буссинеска


—
коэффициента Кориолиса
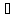
кинетической энергии
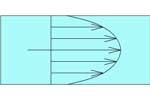
Величина
обоих коэффициентов зависит от характера
распределения скоростей в поперечном
сечении потока жидкости. На практике
при турбулентном режиме движения
коэффициент Кориолиса


Поэтому обычно полагают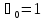
Однако встречаются отдельные случаи,
когда
пренебрежение им может привести к
значительным погрешностям.
Пример
3.2. Определить
силу воздействия потока жидкости на
преграду. Пусть жидкость вытекает в
атмосферу и наталкивается на безграничную
стенку, установленную нормально к
потоку. В результате жидкость растекается
по стенке, изменяя направление своего
течения на 900
(рис.
3.8). Известны площадь сечения потока

скорость истечения
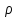
Рис. 3.8. Воздействие
струи на преграду
Для
решения данной задачи берём фиксированный
объём, показанный штриховой линией, и
применяем теорему Эйлера. Так как
давление внутри струи и по поверхности
жидкости равно атмосферному, т.е.
избыточное давление равно нулю, уравнение,
выражающее теорему Эйлера, для направления,
совпадающего с вектором скорости
истечения
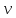
будет иметь вид

или 
Это
и есть сила воздействия потока жидкости
на преграду. При другом угле установке
стенки или других её форме и размерах
в правую формулы (3.11) вводится безразмерный
коэффициент, отличный от единицы, но
пропорциональность силы

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Смачиваемый периметр — это одно измерение, используемое для анализа русла реки и русла реки. Это общее линейное расстояние в поперечном сечении реки или ручья, которое находится в контакте с водой. Измерение смачиваемого периметра легко, если русло ровное и гладкое, как бетонный дренажный канал, но речные и русла рек редко бывают. Сложные контуры требуют серии измерений глубины, которые затем используются для расчета смачиваемого периметра. Чем больше измерений проведено для данного сечения, тем точнее будет оценка.
-
Если кровать неровная и неровная, вам потребуется больше измерений с более короткими интервалами, чтобы получить точный результат.
Прикрепите строку к вершине нижнего берега потока. Протяните струну поперек ручья перпендикулярно и прикрепите ее к другому берегу. Строка должна быть горизонтальной, поэтому используйте уровень для проверки и исправления. Если вы проводите измерения в глубокой реке или озере, вы, вероятно, будете использовать лодку и эхолот, а не струну и линейку.
Выполните измерения глубины с равными интервалами вдоль струны. Будет легче, если у вас есть партнер, который записывает данные во время измерений. Для глубокой воды вам потребуется точная навигационная система, которая поможет вам при проведении измерений с помощью эхолота.
Рассчитайте смоченный периметр каждого интервала. Если бы глубина на одной стороне интервала (D1) составляла 2 фута, глубина на другой стороне (D2) составляла 4 фута, а интервал (W) составлял 6 дюймов, расчет был бы: P = SQRT ((D2- D1) ^ 2 + W ^ 2) P = SQRT ((4 — 2) ^ 2 + 0, 5 ^ 2) Примечание: 6 дюймов = 0, 5 фута P = SQRT (4, 25) = 2, 06 фута
Добавьте смачиваемые периметры для всех интервалов, чтобы получить общий смачиваемый периметр для этого поперечного сечения.
подсказки
На поток воды через реку или трубу влияет множество факторов, и одним из наиболее важных из них является гидравлический радиус. Это зависит от общей площади поперечного сечения корпуса и того, что называется смоченный периметр, который, по сути, показывает, какая часть стен корпуса контактирует с водой.
Расчет периметра смачивания не всегда прост, поскольку он сильно зависит от формы резервуара и уровня воды. Если вы не можете напрямую измерить смоченный периметр, вам нужно будет оценить его, используя форму, которая примерно соответствует форме резервуара.
Что такое смоченный периметр?
Смачиваемый периметр реки или другой емкости с водой является частью периметра площади поперечного сечения емкости. Если быть более точным, это часть поперечного сечения, непосредственно контактирующая с водой, поэтому она простирается по всему дну воды и вверх по сторонам до точки, соответствующей поверхности воды. вода.
Это немного отличается от расчета площади поперечного сечения контейнера, хотя есть некоторые сходства с точки зрения необходимой информации.
Расчет периметра смачивания — Общие положения
Чтобы рассчитать смоченный периметр, вам нужно либо оценить его, либо измерить длину каждой из сторон реки или емкости, контактирующих с водой. Общая формула для смоченного периметра п является:
P = sum_i l_i
Где ля это длина стороны я, и сумма проходит по всем сторонам, контактирующим с водой. В принципе эту формулу довольно просто использовать, но на практике найти нужную информацию непросто. Если вы на самом деле находитесь там, где находится вода и соприкасающиеся с ней поверхности, самый простой способ Чтобы найти смоченный периметр, нужно физически измерить все соответствующие стороны и сложить их.
Однако в некоторых случаях — например, для реки — это создает свои собственные проблемы, и оценка периметра может быть более практичным способом решения проблемы.
Приближение как трапеция
Во многих случаях площадь поперечного сечения воды в реке можно приблизительно представить как трапецию с более короткой стороной в качестве основания вдоль русла реки. Формула для определения смоченного периметра в этом случае:
P = b + 2 Bigg ( bigg ( frac {(T — b)} {2} bigg) ^ 2 + h ^ 2 Bigg) ^ {1/2}
Где б длина основания, Т длина вершины (от берега до берега) и час высота воды. Опять же, найти значения для них может быть непросто, но вы можете оценить, сложно ли получить информацию в противном случае.
Приближение в виде прямоугольника
Прямоугольник проще рассчитать периметр смачивания, но большинство естественных водных потоков имеют наклонные берега, и поэтому их лучше аппроксимировать как трапецию. Однако, если у вас есть резервуар, который можно представить в виде прямоугольника, математика будет намного проще:
P = b + 2h
Где б это база и час высота воды.
Приближение как круг
Если вы рассматриваете поток воды через трубу или другую форму, вы думаете, что это можно точно аппроксимировать как поперечного сечения части окружности можно рассчитать смоченный периметр по формуле длины дуги окружности.
Если вы выполняете расчеты для трубы, вы, вероятно, узнаете диаметр (и, следовательно, радиус) трубы из ее технических характеристик, что значительно упрощает процесс. Формула длины дуги (с углом, измеренным в радианах):
P = θr
Где θ угол в центре круга, покрытого дугой, содержащей воду и р это радиус. Например, если вода заполняет половину круглого поперечного сечения, это π радиан, что дает смоченный периметр π_r_ = π_d_ / 2, где d диаметр трубы.
Другими словами, как и следовало ожидать, смоченный периметр в этом случае составляет половину окружности круга. Учитывая, что в круге 2π радиан, полная труба будет иметь смоченный периметр, равный 2 π_r_ — окружности круга.
Дабы узнать периметр пруда, необходимо сложить все отрезки, ограничивающие многоугольник на плане.
Смотрим на чертёж. Мы видим, что длины двух отрезков нам не известны — они прочерчены красным цветом — их нужно вычислить.
Общую длину пруда находим, сложив отрезки в верхней части:
12+9=21 (м).
Вычтя из общей длины нижний левый отрезок (16 м), находим неизвестный правый (красный) отрезок в нижней части пруда:
21-16=5 (м).
Теперь найдём вертикальный неизвестный отрезок (красный) вверху справа. Для этого сначала вычислим узкую горловину в средней части пруда (синий размер), вычтя из правой стороны пруда вертикальный отрезок внизу, равный 5 м.
14-4=10 (м)
Теперь вычтем этот размер из левой стороны пруда и получим второй неизвестный (красный) отрезок:
14-10=4 (м)
Собственно это и так видно из чертежа, поскольку левая и правая стороны пруда равны.
Отрезка по 14 м — два. Стало быть 14х2. Отрезков по 4 м также два, значит 4х2. Пишем сумму сторон. Для удобства слева направо: 14х2 + 12 + 4х2 + 9 + 5 +16 = 78 (м). Ответ: периметр пруда равен 78 м.
2018-03-27
Живое сечение, гидравлический радиус и смоченный периметр в гидравлике
Содержание:
- Живое сечение
- Смоченный периметр
- Гидравлический радиус
- Гидравлический радиус для круглой трубы
- Гидравлический диаметр
Живое сечение
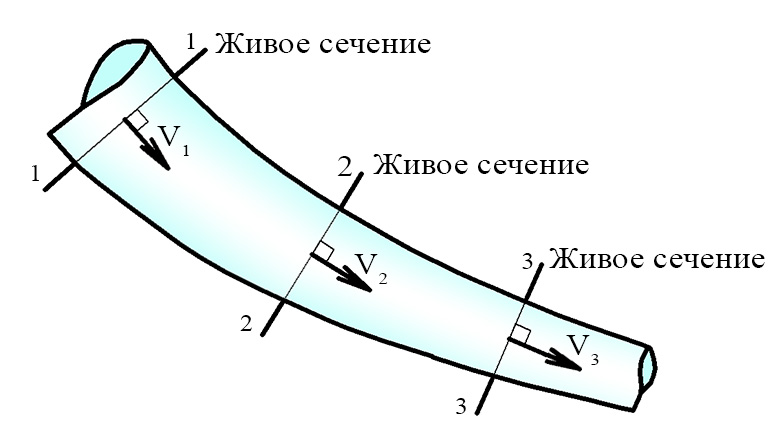
Живым или нормальным называют сечение потока перпендикулярное направлению скорости течения (линиям тока).
На рисунке изображен поток жидкости, в произвольных точках выбраны перпендикулярные направлениям скоростей живые сечения 1-1, 2-2, 3-3.
Смоченный периметр
Периметр контакта жидкости в данном живом сечении называют смоченным периметром (П, м).
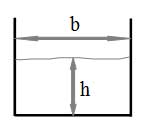
Рассмотрим пример:
Для представленного сечения смоченный периметр можно определить по формуле:
П=2h+b
Гидравлический радиус
Отношение площади живого сечения (А, м2) к смоченному периметру (П, м) называют гидравлическим радиусом.
Rг=А/П, м
Гидравлический радиус для круглой трубы
Рассмотрим трубу с внутренним диаметром d, полностью заполненную жидкостью.
П=π d
A=π d2/4
Rг=d/4, м
Гидравлический диаметр
Для заполненной круглой трубы гидравлический диаметр можно определить по формуле:
Dг=4Rг, м
Читайте также:
Все новости