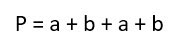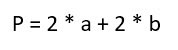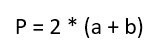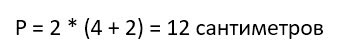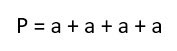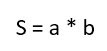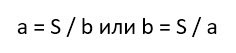|
Если представить, что ваш огород прямоугольной формы и вам необходимо участок обложить забором, то наверное перед вами возникнет вопрос, а какой длины будет забор, чтобы правильно рассчитать расход стройматериалов. Вы сложите длины сторон забора и найдете ПЕРИМЕТР. Если зададитесь вопросом, какое количество земли нужно перекопать на этом участке, то придется искать ПЛОЩАДЬ, а для этого нужно будет перемножить длину на ширину участка, ведь как известно у прямоугольника противоположные стороны попарно равны. Не стоит забывать, что квадрат тоже прямоугольник, чтобы найти периметр квадрата, нужно длину умножить на 4, а площадь — длину стороны умножить на себя. система выбрала этот ответ лучшим Для того, чтобы находить периметр и площадь прямоугольника, нужно знать формулы и главное — уметь применять их для решения задач — ведь они бывают разной сложности. Очень часто при решении задач легкого уровня достаточно знать основные формулы и решить их просто подставляя нужные значения. Если задачи посложнее и в их условии нет данных нужных для формулы, нужно их находить с помощью других алгебраических действий. В этом случае можно навести следующий пример нужно найти площадь прямоугольника, если его периметр равен 120 см, а стороны относятся как 2 к 3 сначала составляем уравнение, чтобы найти стороны используя при этом формулу периметра (P=2(а+b): 2*(2х+3Х)=120 решаем его, х=12 значит стороны равны 24 см и 36 см и теперь уже подставляем значения в формулу площади S=ab и находим ее S=24*36=864 см.кв. Leona-100 6 лет назад Вспомним школьный курс математики. Так периметр прямоугольника находится по формуле суммы двух его сторон умноженных на 2. То есть Р=2*(а+b), где а и b это стороны прямоугольника. Площадь, соответственно находится с помощью формулы S=a*b, где a и b также являются его сторонами. Если у прямоугольника заданы две противолежащие стороны, то все просто перемножаем их и получаем площадь, складываем и удваиваем и получаем периметр. Однако чаще в учебниках задают самый разнобой — сторону и периметр, сторону и площадь, сторону и диагональ. Как поступать в этих случаях. Вот это идеальная задача. Могут быть заданы сторона и диагональ. В этом случае находим вторую сторону по теореме Пифагора — как второй катет в треугольнике где гипотенуза диагональ прямоугольника. В итоге мы имеем вот какие формулы для нахождения периметра прямоугольника: А если по простому преобразовать эти же формулы, то получаются формулы для нахождения площади во всех вариантах задач: Oleg74 8 лет назад Если не вдаваться в глубокие подробности, то найти площадь и периметр геометрической фигуры прямоугольник очень просто. Обозначим стороны такого прямоугольника латинскими буквами : a, b, c и d. Пусть a = c — это длина прямоугольника, а b и d — это ширина прямоугольника. Площадь прямоугольника : S = a x b Периметр прямоугольника : S = a + b + c + d Румия Тенишева 9 лет назад Площадь прямоугольника равна произведению длины и ширины и вычисляется по формуле a*b, где а и b -стороны прямоугольника. Периметр прямоугольника равен сумме всех его сторон и вычисляется по формуле a+b+a+b. Nelli4ka 6 лет назад Периметр прямоугольника — это длины всех его сторон. Исходя из того, что у этой фигуры четыре стороны, или две пары, при этом противолежащие стороны равны друг другу, можно прийти к выводу, что уместно сложить значения двух разновеликих сторон и умножить полученное значение на два. Площадь находится также просто: мы просто перемножаем разновеликие стороны. Нахождение площади прямоугольника — умножим длину прямоугольника на его ширину. Нахождение периметра прямоугольника (сумма длин всех сторон) — простым сложением длин всех сторон, либо к длине продольной стороны прямоугольника, прибавляем длину поперечной и полученную сумму умножаем на два. Ksyusha26 8 лет назад Можно пойти самым простым путем нахождения площади прямоугольника. А именно, умножить длину прямоугольника (как правило, это «a») на ширину прямоугольника (как правило, это «B»). А вот периметр ищем при помощи сложения всех сторон, или, проще говоря : 2a+2b ЛИСА-НАСА 6 лет назад Площадь прямоугольника рассчитывается путем умножения его длины на ширину полученное произведение и будет площадь. Периметр прямоугольника находится путем суммирования длины и ширины, полученную сумму нужно еще умножить на два, это и будет искомый периметр. Luizbon 9 лет назад Площадь вычисляется при умножении длинной стороны прямоугольника с короткой. А периметр-это (длин. сторона+ кор. сторона)*2 Знаете ответ? |
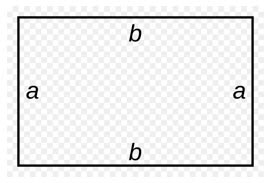
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длиной его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a=b) именуется квадратом.
Характеристики прямоугольника
Параллельность сторон, одинаковость углов и возможность замощения плоскости делают прямоугольник самой комфортной геометрической фигурой при разбиении площади на участки будь то на местности, в помещении либо снутри технического устройства. Участок есть возможность считать прямоугольным, в том случае его отличия от безупречного прямоугольника не превосходят допустимой в расчетах погрешности. Тогда для периметр и площадь участка есть возможность определять по формулам расчета периметра и площади прямоугольника.
Периметр P прямоугольника равен двойной сумме сторон, прилежащих к одному углу
P = 2(a + b).
Длина диагонали d прямоугольника рассчитывается по аксиоме Пифагора:
d = √(a2 + b2).
Углы меж диагоналями прямоугльника определяются соотношением сторон:
α = 2arctg(a/b),
β = 2arctg(b/a),
α + β = 180°.
Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу (произведению длины на ширину):
S = a·b.
Также есть возможность выразить площадь прямоугольника через длину диагоналей и угол меж ними:
S = d2·sin(α/2)·cos(α/2).
Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали:
R = √(a2 + b2)/2.
В прямоугольник (в том случае он не квадрат) нельзя вписать окружность так, чтоб она касалась всех его сторон. Наибольший радиус окружности, которая может поместиться снутри прямоугольника, равен половине его наименьшей стороны.
Источники:
Глядеть также:
Периметр прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.
Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.
Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:
А частным случаем прямоугольника является квадрат:
У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, жир слово пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
Как найти периметр прямоугольника
Возьмем для примера такой прямоугольник:
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.
Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:
С учетом равенства сторон, формулы можно существенно упростить:
или
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
или
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Другие формулы для расчета периметра прямоугольника
Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.
Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.
Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:
Вместо заключения
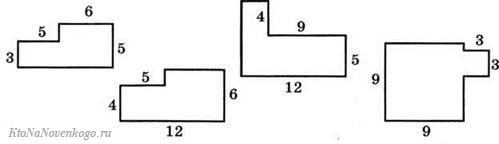
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.
Вот и все, что мы хотели сегодня рассказать.
 Популярные ответы
Популярные ответы
- Когда буквы е, ё, ю, я обозначают два звука?
- Каким членом предложения может быть местоимение?
- Как правильно произносятся слова термин, шинель, темп?
- Как найти точки экстремума функции по графику производной?
- Как правильно: по средам (ударение на «а» или на «е»)?
- Какой официальный сайт Московского энергетического института (МЭИ)?
- На какие вопросы отвечает наречие?
- Где найти примеры сравнительных оборотов и других конструкций со словом «как»?
- Как в физике обозначается скорость движения?
- Где скачать задания по английскому языку олимпиады для школьников «Покори Воробьевы горы!»?
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длиной его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a=b) называется квадратом.
Свойства прямоугольника
- противолежащие стороны равны и параллельны друг другу;
- диагонали равны и в точке пересечения делятся пополам;
- сумма квадратов диагоналей равна сумме квадратов всех (четырех) сторон;
- прямогугольниками одного размера можно полностью замостить плоскость;
- прямоугольник можно двумя способами разделить на два равных между собой прямоугольника;
- прямоугольник можно разделить на два равных между собой прямогульных треугольника;
- вокруг прямоугольника можно описать окружность, диаметр которой равен диагонали прямоугольника;
- в прямогульник (кроме квадрата) нельзя вписать окружность так, чтобы она касалась всех его сторон.
Параллельность сторон, одинаковость углов и возможность замощения плоскости делают прямоугольник самой удобной геометрической фигурой при разбиении площади на участки будь то на местности, в помещении или внутри технического устройства. Участок можно считать прямоугольным, если его отклонения от идеального прямоугольника не превышают допустимой в расчетах погрешности. Тогда для периметр и площадь участка можно определять по формулам расчета периметра и площади прямоугольника.
Периметр P прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу
P = 2(a + b).
Длина диагонали d прямоугольника вычисляется по теореме Пифагора:
d = √(a2 + b2).
Углы между диагоналями прямоугльника определяются соотношением сторон:
α = 2arctg(a/b),
β = 2arctg(b/a),
α + β = 180°.
Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу (произведению длины на ширину):
S = a·b.
Также можно выразить площадь прямоугольника через длину диагоналей и угол между ними:
S = d2·sin(α/2)·cos(α/2).
Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали:
R = √(a2 + b2)/2.
В прямоугольник (если он не квадрат) нельзя вписать окружность так, чтобы она касалась всех его сторон. Максимальный радиус окружности, которая может поместиться внутри прямоугольника, равен половине его меньшей стороны.
Источники:
- Прямоугольник — Википедия
- Четырехугольники — на сайте Омского университета
Дополнительно от Генона:
- Как найти площадь и периметр квадрата?
- Как найти площадь прямоугольного треугольника?
- У каких многоугольников все диагонали равны между собой?
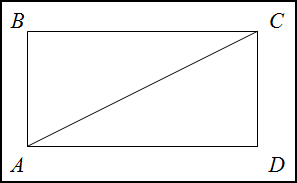
Задание. Стороны прямоугольника относятся как
$3:4$, а диагональ равна
5 м. Найти периметр прямоугольника.
Решение. Сделаем рисунок.
По условию $AB:BC=3:4$. Пусть
$x$ — коэффициент пропорциональности, тогда
$AB=3x$,
$BC=4x$. Рассмотрим
$Delta A B C$ — прямоугольный. По теореме Пифагора имеем:
$AB^2 + BC^2 = AC^2$
После подстановки данных получим уравнение относительно $x$:
$$(3 x)^{2}+(4 x)^{2}=5^{2}$$
$$9 x^{2}+16 x^{2}=25$$
$$25 x^{2}=25$$
$$x^{2}=1 Rightarrow x=1$$
То есть
$AB=3$ м и
$BC=4$ м. Искомый периметр равен:
$P_{Delta A B C D}=2 cdot(3+4)=2 cdot 7=14$ (м)
Ответ. $P_{Delta A B C D}=14$ (м)