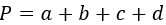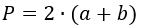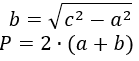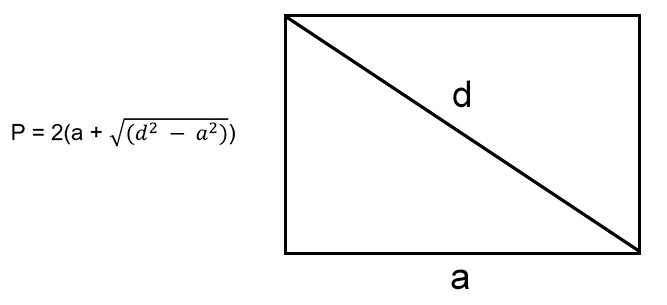|
Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам: Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим Ксарфакс 4 года назад Периметр по координатам Периметр фигуры — это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2): Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой:
Sadness 4 года назад Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так:l=sqrt((x2 — x1)^2 + (y2 — y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере:Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((12 — 1)^2 + ((-5) — 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((-2 — 12)^2 + (1 — -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 — (-2))^2 + (8 — 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты. Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым — просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула: , где х1 и х2 — координаты концов отрезка по оси х, а y1 и y2 — координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины. Hamster1337 2 года назад Периметр геометрических фигур по координатам вершин можно найти при помощи формулы Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр. Алиса в Стране 3 года назад Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр — сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула: где точка А имеет координаты (x1; y1), а точка В — координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС. габбас 4 года назад Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 — x1^2) + (y2^2 — y1^2), х1 и у1 координаты начала, х2,у2 — координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюминка 3 года назад Во-первых, вспомним, что такое периметр — это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb — xa)2 + (yb — ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2): Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить — получить. Бекки Шарп 3 года назад Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле: У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле. Складываем полученные результаты и получаем периметр. Бархатные лапки 3 года назад Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр. Знаете ответ? |
Периметр прямоугольника калькулятор онлайн умеет вычислять периметр двумя способами:
- По двум сторонам.
- По диагонали и одной стороне.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Периметр прямоугольника — это сумма всех его сторон.
Так как у прямоугольника противоположные стороны равны, то так же периметр — это удвоенная сумма его длины и ширины.
Как найти периметр прямоугольника?
Найти периметр прямоугольника очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По четырем сторонам
где a,b,c,d — стороны прямоугольника.
2) По двум сторонам
где a,b — стороны прямоугольника.
3) По диагонали и одной стороне
где a — любая из сторон, с — диагональ прямоугольника.
Скачать все формулы в формате Word
Периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
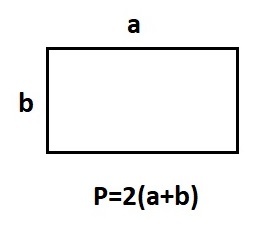
(P=2(a+b))
где (a) и (b) — это две соседние стороны фигуры.
По любой стороне и площади
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
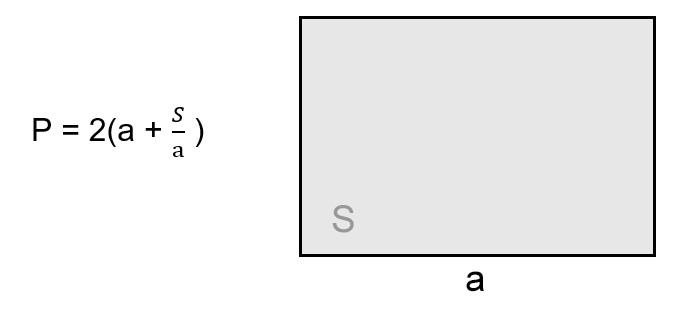
Так как площадь прямоугольника — это произведение двух его смежных сторон ((S=atimes b)), чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: (b=frac Sa).
Получается, что формула для расчета (P) рассматриваемой фигуры будет выглядеть следующим образом:
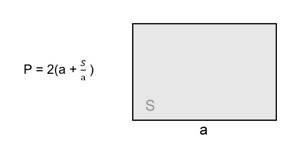
(P=2(frac Sa+a))
По любой стороне и диагонали
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
(b=sqrt{d^2-a^2})
где (d) — диагональ прямоугольника, а (b) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
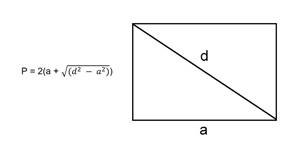
(P=2(a+sqrt{d^2-a^2}))
По любой стороне и радиусу описанной окружности
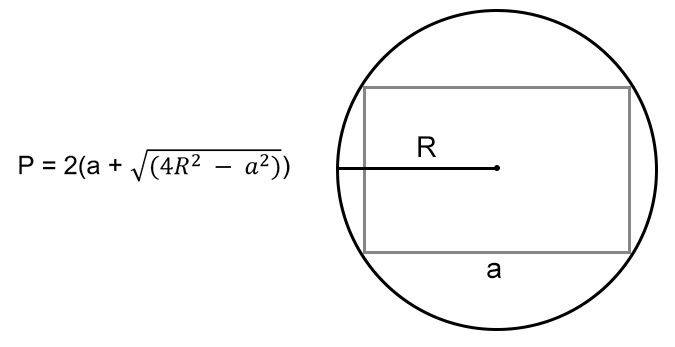
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
(b=sqrt{4R^2-a^2})
где (R) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
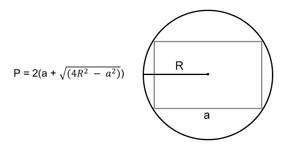
(P=2(a+sqrt{4R^2-a^2}))
Примеры решения задач
Задача 1
Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.
Решение:
Применяем самую первую формулу для расчета:
(P=2(a+b))
Получается:
(P=2(5+7)=24) см
Ответ: 24 см.
Задача 2
Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 (см^2), одна из его сторон равна 6 см. Вычислить Р фигуры.
Решение:
Берем формулу (P=2(frac Sa+a)) и подставляем известные значения:
(P=2(frac{24}6+6)=2times10=20) см
Ответ: 20 см.
Задача 3
Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.
Решение:
Вспоминаем формулу для расчета (P=2(a+sqrt{d^2-a^2})) и вставляем известные величины:
(P=2;(3+sqrt{5^2-3^2})=2(3+sqrt{25-9})=2times7=14) см
Ответ: 14 см.
Задача 4
Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.
Решение:
В этом случае для расчета суммы длин всех сторон применяем формулу (P=2(a+sqrt{4R^2-a^2})). Используем известные значения и получаем:
(P=2;(3+sqrt{4times5^2-3^2})=2(3+sqrt{100-9})=2(3+sqrt{91})=6+2sqrt{91}) см.
Ответ: (6+2sqrt{91}) см.
Вас ждут четыре простых способа.
Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному. Выбирайте формулу в зависимости от известных вам данных.
Зная все или две соседние стороны
Для полноты упомянем простейшие классические формулы.
- Если известна длина всех сторон прямоугольника, просто посчитайте сумму этих величин.
- Если вы знаете только две соседние стороны, суммируйте их и умножьте результат на два.
- P — искомый периметр;
- a, b, c, d — стороны прямоугольника.
Сейчас читают 🔥
Зная любую сторону и площадь
- Поделите площадь на длину известной стороны.
- Прибавьте результат к известной стороне.
- Умножьте полученное число на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- S — площадь прямоугольника.
Зная любую сторону и диагональ
- Посчитайте разность квадратов диагонали и стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- d — диагональ прямоугольника.
Зная одну любую сторону и радиус описанной окружности
- Умножьте квадрат радиуса на четыре.
- Посчитайте разность полученного числа и квадрата известной стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- R — радиус окружности, описанной вокруг прямоугольника.
Началом пропедевтики изучения геометрии являются знания, которые учащиеся получают, переходя во 2 класс. Применяя правила умножения, здесь впервые вычисляют периметр прямоугольника.
Переходя в следующий, 3 класс, школьники на основе этой формулы начинают знакомиться с правилами раскрытия скобок.
Как вычислить периметр прямоугольника
Учитывая, что периметр любой фигуры есть сумма длин её сторон, выводят две формы записи для нахождения этой величины.
В прямоугольнике противоположные стороны равны, поэтому, обозначив смежные стороны a и b, получают по определению:
откуда после приведения подобных слагаемых, вытекает формула
или, вынося двойку за скобки,
Рассматривая квадрат, как прямоугольник с равными сторонами, получают формулу его периметра:
Стандартный метод
В зависимости от сложности вычислений, применяют одну из формул, чтобы высчитать периметр. Учащиеся начальной школы знакомятся с понятием, сталкиваясь с практическими задачами.
Задача
Найти длину забора участка прямоугольной формы, который надо построить Сидору Карловичу, если общая граница с участком Ивана Петровича составляет 3 метра, а с плантацией Марии Ивановны – 5 метров.
Решение
Чтобы решить задачу и помочь незадачливому Сидору Карловичу, ученику приходится использовать формулу периметра прямоугольника. Учитывая, что a = 3, b = 5, дети легко находят, что длина забора равна
P = 2 (a + b) = 2 * (3 + 5) = 2 * 8 = 16 (метров)
Важные требования, предъявляемые к ученикам на данном этапе изучения материала, заключаются в правильном соизмерении длины и ширины, а также в умении начертить фигуру.
Работа выполняется только при одинаковых единицах измерения, все чертежи делаются строго с использованием инструментов!
Часто длина заданного отрезка измеряется непосредственно.
Нахождение периметра через площадь и одну сторону
При более близком знакомстве с прямоугольником, способы нахождения его периметра начинают варьироваться в зависимости от исходных данных в задаче.
Если известны одна из сторон и площадь, то, чтобы узнать, чему равен периметр, выражается неизвестная сторона, а затем она подставляется в формулу.
то есть, соотношение площади и периметра при известной стороне есть
Как найти периметр прямоугольной фигуры
В начальной школе для запоминания принципа детям часто предлагается понятие «неправильного четырёхугольника» (не прямоугольника).
Для нахождения его периметра предлагается рассчитать сумму длин сторон непосредственно, предварительно измерив каждую из них.
Для любой более сложной фигуры производят разбиение, если возможно, на небольшие прямоугольники, с которыми и работают.
Заключение
Современный онлайн калькулятор позволяет ввести значения сторон и задать необходимую точность вычислений, мгновенно производя расчёт и выдавая необходимый результат.
Основные определения
Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.
Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула нахождения периметра прямоугольника
Способ вычисления нужно выбрать, отталкиваясь от исходных данных. Далее рассмотрим четыре классические формулы.
Когда известны все или две соседние стороны
P = a + b + c + d, где a, b, c, d — стороны.
Когда известна любая сторона и площадь
P = 2 * (a + S : a), где a — сторона, S — площадь.
Площадь — это плоскость внутри замкнутой геометрической фигуры.
Когда известна любая сторона и диагональ
P = 2 * (a + √(d 2 — а 2 )), где a — сторона, d — диагональ.
Диагональ — это отрезок, который соединяет противоположные стороны фигуры.
Когда известна одна любая сторона и радиус описанной окружности
P = 2 * (a + √(4 * R 2 — a 2 )), где a — сторона, R — радиус окружности.
Радиус — отрезок, соединяющий центр и любую точку окружности.
Решение задач
А теперь практиковаться!
1. Одна сторона прямоугольника 9 см, а другая на 11 см длиннее. Как узнать периметр?
- Если a = 9, то b = 9 + 11;
- Тогда b = 20 см;
- Воспользуемся формулой P = 2 * (a + b);
- P = 2 * (9 + 20);
2. Площадь прямоугольника составляет 60 м², ширина равна 15 м. Чему равен периметр фигуры?
- Для использования формулы P = 2 * (a + b), нам нужно найти длину;
- Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 60 : 15 = 4;
- Далее подставляем известные переменные в формулу: (15 + 4) * 2 = 38;
А еще можно вот так:
- Воспользуемся формулой P = 2 * (a + S : a);
- P = 2 * (15 + 60 : 15);
Ответ — такой же, 38 м.
3. Как найти периметр прямоугольника, если его диагональ в два раза больше длины равной 8 см?
- Если a = 8, то d = 8 *2;
- Тогда d = 16;
- Воспользуемся формулой P = 2 * (a + √(d 2 — а 2 ));
- P = 2 * (8 + √(16 2 — 8 2 ));
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Вместо скучных учебников ученики проходят интерактивные задания с автоматической проверкой, рисуют вместе с учителем на онлайн-доске и задают вопросы, которые бывает неловко спросить перед всем классом.
Консультации по выполнению всех типов работ
- Периметр прямоугольника
- Варианты нахождения периметра прямоугольника
- По сторонам
- По любой стороне и площади
- По любой стороне и диагонали
- По любой стороне и радиусу описанной окружности
- Примеры решения задач
- Задача 1
- Задача 2
- Задача 3
- Задача 4
- Периметр прямоугольника
- Варианты нахождения периметра прямоугольника
- По сторонам
- По любой стороне и площади
- По любой стороне и диагонали
- По любой стороне и радиусу описанной окружности
- Примеры решения задач
- Задача 1
- Задача 2
- Задача 3
- Задача 4
Периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
где (a) и (b) — это две соседние стороны фигуры.
По любой стороне и площади
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
Так как площадь прямоугольника — это произведение двух его смежных сторон ((S=atimes b)) , чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: (b=frac Sa) .
Получается, что формула для расчета (P) рассматриваемой фигуры будет выглядеть следующим образом:
По любой стороне и диагонали
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
где (d) — диагональ прямоугольника, а (b) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
По любой стороне и радиусу описанной окружности
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
где (R) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
Примеры решения задач
Задача 1
Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.
Решение:
Применяем самую первую формулу для расчета:
Задача 2
Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 (см^2) , одна из его сторон равна 6 см. Вычислить Р фигуры.
Решение:
Берем формулу (P=2(frac Sa+a)) и подставляем известные значения:
Задача 3
Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.
Решение:
Вспоминаем формулу для расчета (P=2(a+sqrt)) и вставляем известные величины:
Задача 4
Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.
Решение:
В этом случае для расчета суммы длин всех сторон применяем формулу (P=2(a+sqrt<4R^2-a^2>)) . Используем известные значения и получаем:
Работы любой сложности
Квалифицированная помощь от опытных авторов
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются
длинами его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b)
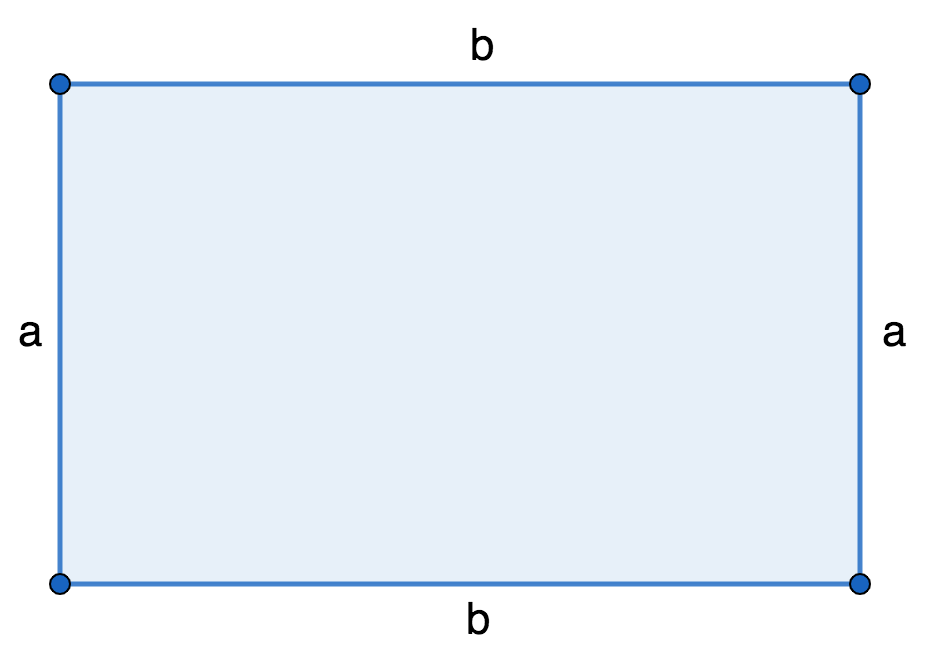
Периметр прямоугольника ABCD равен сумме
сторон умноженной на 2, прилежащих к одному углу.
где P — периметр прямоугольника,
a — длина первой стороны,
b — длина второй стороны.
Как найти периметр прямоугольника другими способами? Ниже приведены формулы, по которым можно
найти периметр прямоугольника, через разные данные.
Формула периметра прямоугольника через две стороны прямоугольника:
Формула периметра прямоугольника через площадь и любую сторону:
Формула периметра прямоугольника через диагональ и любую сторону:
Формула периметра прямоугольника через радиус описанной окружности и любую сторону:
Формула периметра прямоугольника через диаметр описанной окружности и любую сторону:
Основные свойства прямоугольника.
- Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
- Противоположные стороны прямоугольника параллельны:
- Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
- Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
- Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
- Диагонали прямоугольника имеют одинаковой длины:
- Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d 2 = 2a 2 + 2b 2
- Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на
- Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
AO = BO = CO = DO = d/2
- Точка пересечения диагоналей называется центром прямоугольника и также является центром
- Диагональ прямоугольника является диаметром описанной окружности.
- Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов
равна 180 градусов:
∠ABC = ∠CDA = 180° ∠BCD = ∠DAB = 180°
- В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы
противоположных сторон не равны между собой (вписать окружность можно только в частный случай
В данной публикации мы рассмотрим, каким образом можно посчитать периметр прямоугольника и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
Периметр (P) прямоугольника равняется сумме длин всех его сторон.
P = a + b + a + b
Т.к. противоположные стороны данной фигуры равны, формулу можно представить в следующем виде:
- Удвоенная сумма сторона: P = 2*(a+b)
- Сумма двойных значений сторон: P = 2a+2b
Короткая сторона – это высота/ширина прямоугольника, более длинная сторона – его основание/длина.
Примеры задач
Задание 1
Найдите периметр прямоугольника, если его стороны равны: 5 и 8 см.
Решение:
Подставляем в формулу известные значения и получаем: P = 2 * (5 см + 8 см) = 26 см.
Задание 2
Периметр прямоугольника равен 20 см, а одна из его сторон – 4 см. Найдите вторую сторону фигуры.
Решение:
Как мы знаем, P=2a+2b. Допустим, 4 см – это сторона а. Значит неизвестная сторона b, умноженная на два, вычисляется так: 2b = P – 2a = 20 см – 2 * 4 см = 12 см.
Следовательно, сторона b = 12 см / 2 = 6 см.
Прямоугольник — одна из простейших геометрических фигур. Поэтому нахождение периметра и площади очень редко становится проблемой — достаточно запомнить несколько простых правил. Проходят тему на начальных уроках геометрии, и со временем информация может выветриваться из памяти. Освежить свои знания очень просто.
Периметр прямоугольника — по каким правилам его находят?
Для того, чтобы найти искомое значение, нужно вспомнить, что называют периметром — и какими особенностями обладают прямоугольники.
- Определение периметра звучит так — это сумма длин всех сторон, сложенных между собой. Записывается показатель буквой Р.
- При этом прямоугольник характерен именно тем, что те из его сторон, которые расположены параллельно друг другу, абсолютно равны.
Находить периметр треугольника — очень простая задача. Достаточно знать всего лишь показатели длины двух сторон, а оставшиеся две стороны будут обладать такими же значениями.
Существуют две формулы для вычисления периметра:
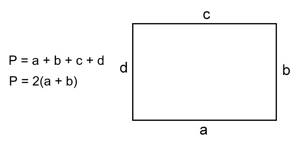
- сложение всех сторон — в данном случае в абстрактном прямоугольнике ABCD стороны AB, BC, CD и AD последовательно складывают друг с другом и получают результат;
- сложение длины и ширины и умножение суммы на 2 — здесь используется правило равенства параллельных сторон в прямоугольнике.
Кроме того, нужно помнить о частном случае квадрата, когда равны друг другу все четыре стороны. Тогда длину одной стороны достаточно просто умножить на 4.
Площадь прямоугольника — формула нахождения
Ненамного сложнее вычислить и площадь геометрической фигуры. Площадь принято обозначать буквой S, а измеряют ее в квадратных сантиметрах, миллиметрах или метрах — в отличие от периметра, где используются просто метры, миллиметры и сантиметры.
S = a*b, поэтому для нахождения площади нужно всего лишь знать длину прямоугольника и его ширину — то есть, показатели двух из сторон. Их необходимо умножить между собой и записать ответ в указанных единицах длины.
Еще проще выглядит формула для нахождения площади квадрата. Поскольку стороны геометрической фигуры равны друг другу, показатели длины и ширины будут совпадать. Необходимо взять показатель одной из сторон и возвести его в квадрат. Записывается это следующим образом — S = а2.
При записи решения задач на нахождение периметра или площади рядом с обозначениями Р или S принято ставить маленькие буквенные обозначения конкретной фигуры. Например, Pabcd, или Sabcd. Это позволяет помнить, для какого именно прямоугольника ищется площадь или периметр.
В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.
Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).
Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.
Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.
Показать решение
Показать решение
Показать решение
Показать решение
Показать решение
Показать решение
Показать решение
Показать решение