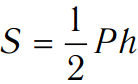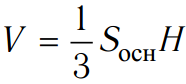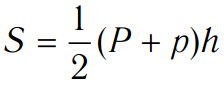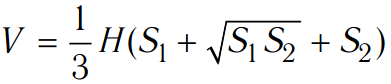Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Задача.
Боковая грань правильной треугольной пирамиды представляет собой правильный треугольник, площадь которого 16 корней из 3 см2 (16√3). Вычислить периметр основания пирамиды.
Решение.
Правильный треугольник — это равносторонний треугольник. Соответственно, боковая грань пирамиды представляет собой равносторонний треугольник.
Площадь равностороннего треугольника равна:
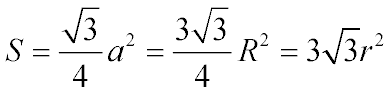
Соответственно:
16√3 = a2 √3 / 4
16 = a2 / 4
a2 = 64
a = 8 см
Основанием правильной треугольной пирамиды является правильный (равносторонний) треугольник. Таким образом, периметр основания пирамиды равен
8 * 3 = 24 см
Ответ: 24 см.
0
Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр |
Описание курса
| Объем правильной треугольной пирамиды
Зная периметр основания правильной пирамиды, можно легко вычислить сторону основания, разделив периметр на удвоенное количество сторон многоугольника. Площадь основания в свою очередь будет рассчитываться по стандартной формуле площади правильного многоугольника, в которую необходимо будет подставить выражение, соответствующее стороне основания через периметр.
a=P/n
S=(na^2)/(4 tan〖(180°)/n〗 )=P^2/(4n tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в правильный многоугольник в основании пирамиды, как и радиус окружности, описанной вокруг основания, необходимо знать сторону основания, поэтому здесь также пригодится полученное через периметр выражение. (рис.34.1,34.2)
r=a/(2 tan〖(180°)/n〗 )=P/(2n tan〖(180°)/n〗 )
R=a/(2 sin〖(180°)/n〗 )=P/(2n sin〖(180°)/n〗 )
Величина внутреннего угла многоугольника в основании зависит только от количества сторон многоугольника и рассчитывается по следующей формуле. (рис.34.3)
γ=180°(n-2)/n
Зная апофему и сторону основания правильной пирамиды, вычисленной через периметр, можно рассчитать боковое ребро и высоту пирамиды по теореме Пифагора в прямоугольных треугольниках. (рис. 34.4, 35.1)
h=√(l^2-r^2 )=√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 )
b=√(l^2+P^2/(4n^2 ))
Чтобы найти угол между основанием и апофемой, а также между основанием и боковым ребром, нужно сначала рассчитать косинусы этих углов в прямоугольных треугольниках, образованных высотой и соответствующим отрезком, которые через основание будут соединяться радиусы вписанной и описанной окружностей. (рис.34.4, 34.5)
cosα=R/b=P/(2n sin〖(180°)/n〗 √(l^2+P^2/(4n^2 )))
cosβ=r/l=P/(2nl tan〖(180°)/n〗 )
Площадь боковой поверхности правильной пирамиды через периметр основания равна произведению периметра на половину апофемы. Площадь полной поверхности вычисляется как сумма полученного значения и площади основания.
S_(б.п.)=lP/2
S_(п.п.)=P(l/2+P/(2n tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо знать не только периметр основания для расчета его площади, но и высоту пирамиды, которая равна квадратному корню из разности квадратов апофемы и радиуса вписанной в основание окружности.
V=1/3 S_(осн.) h=(P^2 √(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))/(12n tan〖(180°)/n〗 )
Сфера, которую можно вписать в пирамиду, должна иметь радиус, равный отношению трех объемов к площади полной поверхности, которые можно вычислить через периметр и апофему пирамиды. Радиус сферы, которую можно описать вокруг пирамиды, должен быть равен квадрату боковой стороны, деленному на удвоенную высоту. (рис.34.6, 34.7)
r_1=3V/S_(п.п.) =(P√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))/(2n tan〖(180°)/n〗 (l/2+P/(2n tan〖(180°)/n〗 )) )
R_1=b^2/2h=(2l^2+P^2/n^2 )/(2√(l^2-(P/(2n tan〖(180°)/n〗 ))^2 ))
Как найти периметр треугольной призмы? – Обзоры Вики
Периметр призмы
- Периметр треугольника = a + b + c текст {Периметр треугольника} = a + b + c Периметр треугольника = a + b + c.
- Периметр прямоугольника = 2l + 2w текст {Периметр прямоугольника} = 2l + 2w Периметр прямоугольника = 2l + 2w.
- Площадь поверхности = 2 b + ph текст {Площадь поверхности} = 2b + ph Площадь поверхности = 2b + ph.
Аналогично, как найти площадь поверхности прямой призмы? Формула для нахождения площади поверхности одинакова для всех правильных призм и выглядит следующим образом: Площадь поверхности = 2B + hP. В этой формуле B — площадь одного из оснований, h — высота призмы, а P — периметр основания.
Как найти боковую сторону и площадь поверхности треугольной призмы? Площадь боковой поверхности треугольной призмы равна сумма площадей всех его боковых граней, которые составляют 3 прямоугольника. Боковая площадь призмы высотой h, при которой размеры треугольных оснований равны a, b и c, равна (a + b + c) h.
Во-вторых, что такое треугольная призматическая сетка? Треугольная призма – это призма, состоящая из двух треугольных оснований и трех прямоугольных сторон. Это пятигранник. …Треугольная призма имеет девять различных сетей, как показано выше.
Что такое прямоугольная призма?
Подобно треугольной призме, прямоугольная призма призма с двумя параллельными и конгруэнтными треугольными гранями и тремя прямоугольными гранями, перпендикулярными треугольным. В прямоугольной призме боковые грани должны быть перпендикулярны основаниям.
то что является основанием треугольной призмы? Верхняя и нижняя, которые треугольников, это базы. Эти три прямоугольника называются боковыми гранями. Треугольная призма имеет пять граней, состоящих из двух треугольных оснований и трех прямоугольных боковых граней, а основание также является гранью.
Чему равны боковые грани треугольной призмы? Верх и низ, которые являются треугольниками, являются основаниями.
Как найти недостающую сторону треугольной призмы?
Какие три основания у треугольной призмы?
Обратите внимание, как ваша трехмерная треугольная призма состоит из двухмерных фигур, таких как прямоугольники и треугольники. Есть три прямоугольника и два треугольника. Двумерные фигуры, образующие трехмерную форму, называются гранями. Верх и низ, которые являются треугольниками, являются основаниями.
Сколько линий на треугольной призме? Он имеет в общей сложности 9 ребра, 5 граней и 6 вершин (соединенных прямоугольными гранями).
Что из перечисленного является треугольной призмой?
Например, призма с треугольным основанием называется треугольной призмой, а призма с квадратным основанием называется квадратной призмой и так далее.
…
Треугольная призма.
| 1. | Что такое треугольная призма? |
|---|---|
| 3. | Треугольная призматическая сетка |
| 4. | Часто задаваемые вопросы о треугольной призме |
Какова площадь поверхности треугольной пирамиды?
Чтобы найти площадь правильной треугольной пирамиды, воспользуемся формулой SA = A + (3/2) bh, где A = площадь основания пирамиды, b = основание одной из граней и h = высота одной из граней.
Сколько треугольных граней у треугольной призмы? Треугольная призма имеет пять лиц.
Сколько линий на треугольной призме? Свойства треугольной призмы
Он имеет в общей сложности 9 ребра, 5 граней и 6 вершин (соединенных прямоугольными гранями).
Является ли конус треугольной призмой?
Призма – объемная фигура, имеющая две параллельные конгруэнтные стороны, называемые основаниями, которые соединены боковыми гранями, являющимися параллелограммами. Есть оба прямоугольные и треугольные призмы. … Основание конуса — это круг, и это легко увидеть.
Какова площадь поверхности этой треугольной пирамиды? Чтобы найти площадь поверхности правильной треугольной пирамиды, воспользуемся формулой SA = A + (3/2) bh, где A = площадь основания пирамиды, b = основание одной из граней и h = высота одной из граней.
Чему равна боковая площадь треугольной пирамиды?
Площадь боковой поверхности треугольной пирамиды
Таким образом, площадь боковой поверхности прямоугольной треугольной пирамиды равна 1⁄2 (периметр основания × наклонная высота), которая далее становится 3/2 (сторона × наклонная высота).
Какие бывают виды треугольных призм? В правильная треугольная призма имеет прямоугольную стороны, в противном случае она косая. Однородная треугольная призма — это прямоугольная призма с равносторонними основаниями и квадратными сторонами.
Какая фигура представляет собой треугольную призму?
В геометрии треугольная призма трехсторонняя призма ; это многогранник, состоящий из треугольного основания, переведенной копии и трех граней, соединяющих соответствующие стороны. Прямоугольная призма имеет прямоугольные стороны, в остальном она наклонная.
…
Треугольная призма.
| Равномерная треугольная призма | |
|---|---|
| Свойства | выпуклый |
| Вершина фигура 4.4 .3 |
Сколько существует типов треугольных призм? Треугольная призма – это призма с треугольными основаниями. На рисунке ниже представлены три типа из треугольных призм.
Как определить площадь поверхности и объем треугольной призмы?
Формулы треугольной призмы
- объем = 0.5 * b * h * длина, где b — длина основания треугольника, h — высота треугольника, а длина — длина призмы.
- area = length * (a + b + c) + (2 * base_area), где a, b, c — стороны треугольника, а base_area — это базовая площадь треугольника.
Площадь поверхности пирамиды 10 класс онлайн-подготовка на Ростелеком Лицей
Пирамида, основные понятия и элементы
Вспомним понятие n-угольной пирамиды. Она получается следующим образом: в плоскости лежит n-угольник с вершинами и т. д. Вне плоскости лежит точка Р. Точка Р соединяется с вершинами n-угольника – получаем пирамиду (рисунок 1).
Рис. 1. Пирамида
Определение.
Многогранник , составленный из n-угольника и n треугольников , … называется пирамидой.
Площадь поверхности пирамиды состоит из площади боковой поверхности и площади основания:
Площадь основания пирамиды, площади основных правильных многоугольников
Рассмотрим нахождение площади основания правильной n-угольной пирамиды.
Рис. 2. Нахождение площади n-угольника
Рассмотрим треугольник , в нем найдем угол . Таких углов всего n штук, значит:
Половина этого угла, угол .
Треугольник , где М – середина стороны , прямоугольный. В нем ОМ – радиус вписанной в n-угольник окружности, – радиус описанной окружности. Поскольку у нас задан по условию катет рассматриваемого прямоугольного треугольника () и мы нашли острый угол (), то по соотношениям в прямоугольном треугольнике мы легко найдем все остальные элементы.
Чтобы найти площадь n-угольника, нужно сложить n площадей треугольников вида . Чтобы найти площадь этого треугольника, найдем катет ОМ прямоугольного треугольника :
Площадь треугольника определяется по формуле:
Теперь получим площадь всего n-угольника:
Рассмотрим наиболее распространенные частные случаи:
Площадь правильного треугольника:
Площадь квадрата:
Площадь правильного шестиугольника:
Чтобы нарисовать правильный шестиугольник, удобно пользоваться следующим алгоритмом (рисунок 3):
Построить окружность (зеленая пунктирная линия) Провести диаметр (синяя пунктирная линия) Отметить середины радиусов построенного диаметра Провести через середины перпендикуляры (красные пунктирные линии) Получены вершины шестиугольника – построить шестиугольник.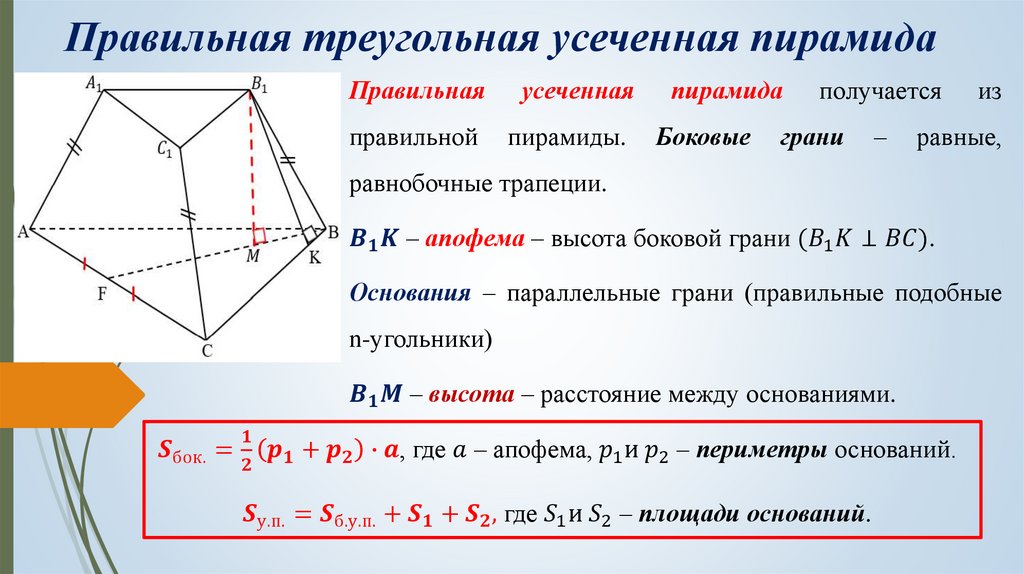
Рис. 3. Правильный шестиугольник
Чтобы найти площадь правильного шестиугольника действуем стандартным методом. Рассматриваем треугольник АОС, в нем находим угол ∠АОВ, таких углов шесть, имеем:
Поскольку отрезки ОА и ОВ равны, то углы ∠ОАВ и ∠ОВА также составляют по . Так, рассматриваемый треугольник правильный. Его площадь нам известна:
Площадь шестиугольника состоит из шести таких площадей:
Площадь боковой поверхности пирамиды
Рассмотрим нахождение площади боковой поверхности правильной пирамиды.
Где – периметр основания; – апофема.
Определение.
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины.
Задача 1
В правильной треугольной пирамиде известна сторона основания и высота. Найти площадь боковой поверхности.
Решение. Проиллюстрируем условие задачи:
Рис. 4. Иллюстрация к задаче 1
Задана правильная пирамида с вершиной Р и основанием АВС.
По вышеприведенной формуле для того, чтобы найти площадь боковой поверхности пирамиды, необходимо найти ее апофему и полупериметр основания. Периметр основания нам известен, так как задана сторона основания. Найдем апофему из прямоугольного треугольника РНО. Один из катетов задан по условию – . Найдем второй катет ОН, он соответствует радиусу вписанной в треугольник окружности, формула нам известна:
Найдем апофему по теореме Пифагора:
Теперь можем найти площадь боковой поверхности пирамиды:
Связь площади треугольника с площадью его проекции
Площадь боковой поверхности и площадь основания пирамиды связаны через величину двугранного угла при основании.
Решение задач
Задача 2
РН – перпендикуляр к плоскости треугольника АВН.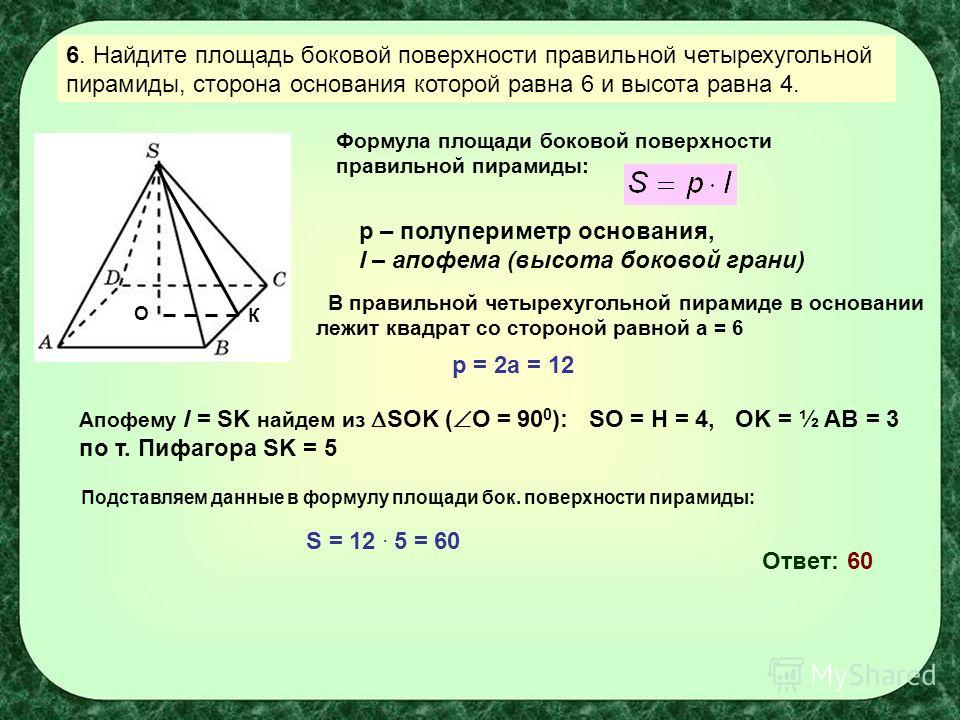
Решение. Проиллюстрируем условие:
Рис. 5. Иллюстрация к задаче 2
Треугольник АВН – это проекция треугольника АВР. Нужно доказать, что площадь проекции есть площадь исходного треугольника на косинус двугранного угла между ними. Поскольку НМ – перпендикуляр к АВ, то и РМ – перпендикуляр к АВ по теореме о трех перпендикулярах. Значит, угол – это линейный угол двугранного угла с ребром АВ. АВР – часть боковой поверхности, АВН – часть основания.
Найдем отношение площадей интересующих нас треугольников:
Рассмотрим прямоугольный треугольник РНМ. В нем РМ – гипотенуза, НМ – катет, прилежащий к заданному углу . Отсюда заключаем:
Что и требовалось доказать.
Задача 3
Доказать для правильной треугольной пирамиды: , где – угол наклона боковой грани к основанию.
Решение. Проиллюстрируем условие:
Рис. 6. Иллюстрация к задаче 3
Задана правильная треугольная пирамида РАВС с основанием АВС и вершиной Р.
Очевидно, что угол наклона боковой грани к основанию пирамиды одинаков для всех боковых граней, то есть если и – середины отрезков ВС, АС и АВ соответственно, то: .
В задаче 2 мы доказали: .
Аналогично:
Выполним сложение полученных выражений.
Что и требовалось доказать.
Задача 4
Боковые грани пирамиды РАВС наклонены к основанию под одним и тем же углом . Докажите, что вершина пирамиды Р проектируется в центр О вписанной в треугольник АВС окружности и что .
Решение. Проиллюстрируем условие задачи:
Рис. 7. Иллюстрация к задаче 4
Пусть РО – высота пирамиды. Найдем место расположения точки О. Из точки О опустим перпендикуляры к сторонам треугольника АВС – .
Поскольку – перпендикуляр к АВ, то по теореме о трех перпендикулярах . Аналогично: и . Тогда – линейный угол двугранного угла при ребре АВ, – линейный угол двугранного угла при ребре ВС, – линейный угол двугранного угла при ребре АС.
Так, точка О равноудалена от сторон треугольника АВС, то есть это центр его вписанной окружности, что и требовалось доказать.
Поскольку РО – высота пирамиды, то треугольники АОВ, АОС, СОВ – это проекции треугольников АРВ, АРС и ВРС соответственно. Имеем (основываясь на задаче 2):
Выполним сложение полученных выражений.
Что и требовалось доказать.
Итак, мы рассмотрели площадь поверхности пирамиды, в частности, площадь основания и площадь боковой поверхности, следующий урок будет посвящен задачам.
Список литературы
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008.
– 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Fmclass.ru (Источник).
- Rapidus.ru (Источник).
- 2mb.ru (Источник).
Домашнее задание
- Задача 1: основанием пирамиды является квадрат, одно из боковых ребер перпендикулярно основанию. Плоскость боковой грани, не проходящей через высоту пирамиды, наклонена к плоскости основания под углом . Наибольшее боковое ребро равно 12 см. Найдите высоту пирамиды и площадь боковой поверхности.
- Задача 2: основанием пирамиды DABC является прямоугольный треугольник АВС, у которого гипотенуза АВ – 29 см, катет АС – 21 см.
Боковое ребро DA перпендикулярно плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.
- Задача 3: основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы и . Найдите площадь поверхности пирамиды.
Как вычислить периметр: часть 2
В предыдущем посте мы узнали, как вычислить периметр любого многоугольника и формулы для правильных многоугольников и прямоугольников. Сегодня мы научимся вычислять периметр других типов многоугольников: ромбов, равнобедренных треугольников, равнобедренных трапеций и ступенчатых многоугольников.
ПРИМЕЧАНИЕ ДЛЯ НАШИХ ЧИТАТЕЛЕЙ В ВЕЛИКОБРИТАНИИ. В этом посте используется термин трапеция, который используется в США
Вычисление периметра:
Ромб
Ромб имеет четыре равные стороны . Но не все его углы равны, а только углов, лежащих друг напротив друга .
Поскольку четыре стороны равны , мы можем умножить длину одной стороны на четыре , чтобы получить периметр.
Периметр = 4 x 5 см = 20 см
Это правило применимо и к квадратам, поскольку у них также четыре равные стороны.
Периметр ромба = 4 x длина одной стороны
Равнобедренный треугольник
Равнобедренный треугольник имеет две равные стороны и одну различную .
Чтобы освежить память о различных типах треугольников, взгляните на этот пост.
Учитывая, что две стороны равны, а одна различна, нам просто нужно умножить длину повторяющейся стороны на два, а затем добавить длину другой стороны.
Периметр = 5см x 2 + 6см = 16см
Итак, для любого равнобедренного треугольника:
Периметр равнобедренного треугольника = длина повторяющейся стороны x 2 + длина другой стороны
Равнобедренная трапеция
Периметр равнобедренных трапеций вычисляется особым образом.
В этом случае нам нужно умножить длину одной из противоположных сторон на два и сложить длины двух оснований.
Периметр = 5см x 2 + 12см + 6см = 28см
Для расчета периметра любой равнобедренной трапеции:
Периметр равнобедренной трапеции = длина противоположной стороны x 2 + длина верхнего основания + длина нижнего основания
Ступенчатый многоугольник
Ступенчатые многоугольники имеют очень своеобразную характеристику. Сумма длин сторон, параллельных основанию, равна длине основания. И то же самое относится к сумме длин сторон, параллельных высоте, которые измеряют ту же длину, что и высота.
Итак, для вычисления периметра любого ступенчатого многоугольника мы можем использовать ту же формулу, что и для прямоугольников, потому что мы можем приблизиться к сумме длин горизонтальной и вертикальной сторон, как если бы они были равны длине основание и высота.
Периметр = 2x (6см + 8см) = 28см
Правило работает для любого ступенчатого многоугольника этого типа:
Периметр ступенчатого многоугольника = 2 х (основание + высота)
Если вы хотите узнать больше об этой теме, геометрии и других материалах по начальной математике, адаптированных к вашему уровню, зайдите на Smartick и попробуйте его бесплатно.
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения от Smartick (см. All)
Площадь и периметра (видео) Формулы для прямоугольников, квадратов и кругов
, написанные
Малкольм Маккинси
11 января 2023
Факт-проверенный на
Paul Mazzola
Площадь и периметр – формулы для прямоугольников, квадратов и кругов
Вы можете использовать площадь квадрата или круга, чтобы найти периметр фигуры (или длину окружности).
Определения
-
Площадь — замкнутое пространство внутри двумерной формы. Форма может быть многоугольником, например, треугольником, квадратом или прямоугольником. Это также может быть криволинейная форма, например, круг. Площадь равна , всегда измеряется в квадратных единицах.
-
Периметр — это расстояние вокруг двумерной формы. Для многоугольников периметр можно найти, используя только сложение путем добавления расстояний по мере перемещения по фигуре.
-
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки. Этот набор точек замыкается во внутреннем пространстве, в области круга. Периметр круга называется его окружностью .
Как найти площадь и периметр
Формулы периметра
-
кв.{2} a = S2 ( S — длина любой стороны.)
-
прямоугольник — A = LWA = LWA = LW ( L и 33333 L и 33333 L и 33333 L и 3 3 3 33333 L и 3 3 L и 3 стороны, длина и ширина).
-
Треугольник — A = 12BHA = FRAC {1} {2} BHA = 21 BH ( B является основой и H — высота.) H — высота.) H — высота.) H — высота.) H — высота.) H — высота.) H . Треугольник – A=s(s−a)(s−b)(s−c)A=sqrt{sleft(s-aright)left(sbright)left(s-cright)}A =s(s−a)(s−b)(s−c) ( a , b , and c are the side lengths, and s is the semiperimeter.
)
-
Parallelogram – A=bhA=bhA= bh ( b – длина основания, а h – высота.)
-
Трапеция – A=b1+b22hA={b}_frac{} {b}_{2}}{2}hA=2b1+b2h (b1{b}_{1}b1 и b2{b}_{2}b2 – длины параллельных сторон, и 9{2}A=πr2 (r – радиус.)
Нахождение периметра по площади включает изменение единиц площади с квадратных (двумерных) единиц на линейные (одномерные) единицы периметра. Форматируя окончательный ответ, не забудьте «возвести в квадрат» единицы измерения, но сохраните ту же систему: см, мм, м, фут, ярд и т. д.
Площадь и длина окружности
На протяжении тысячелетий математики знали, что длина окружности связана с диаметром круга из-за константы π — строчная греческая буква «пи». В математике оно имеет значение, которое никогда не заканчивается и никогда не повторяется, а начинается 3,1415926535 . Для повседневной математики мы обычно используем 3,1415 или даже только 3,14 .
Формула площади и окружности круга
Для C = длина окружности , r = радиус и D = диаметр окружности:
Площадь и длина окружности
Эти две формулы являются одной из математических «трюки» для нахождения периметра, если вы знаете площадь. Формула длины окружности ( 9{2}31 415 м2. Какова его окружность?
Как найти площадь и длину окружности
Периметр и площадь квадрата
Квадрат — это многоугольник; это четырехугольник с четырьмя равными сторонами и четырьмя прямыми углами. Для квадратов можно ускорить процесс вычисления периметра, умножив измерение одной стороны на четыре, где P — периметр, а a — длина стороны:
Периметр и площадь квадрата 9{2}a2 (длина умножается на ширину). Чтобы найти периметр из площади, сначала извлеките квадратный корень из A , чтобы найти длину любой стороны a :
Затем умножьте время измерения этой стороны на 4 , чтобы получить периметр:
Как найти площадь и периметр квадрата
Площадь квадрата 15 129 квадратных миллиметров .
Как найти периметр и площадь квадрата
Тогда:
Площадь и периметр прямоугольника
Прямоугольник – это многоугольник; это четырехугольник, у которого противоположные стороны равны и параллельны.
Площадь и периметр прямоугольника
Площадь прямоугольника
Чтобы найти площадь прямоугольника, нужно умножить длину на ширину.
Периметр прямоугольника
Чтобы найти периметр:
Поскольку квадрат является единственным прямоугольником с четырьмя конгруэнтными сторонами, вам нужно нечто большее, чем просто измерение площади прямоугольника, чтобы найти периметр. Вам нужно измерить любую сторону. 9{2}3015 см 2 и длина одной стороны 45 см 45 см 45 см.
Как найти площадь и периметр прямоугольника
Тогда:
Проверьте свою работу:
Вы сделали это правильно!
Нахождение длин сторон
Вы даже можете найти длины сторон прямоугольника, зная только периметр и площадь. Предположим, у вас есть прямоугольник со следующими известными значениями:
Половина периметра равна одной длине + ширине, поэтому вы знаете, что вам нужно два числа, которые добавляют вместе, чтобы получить 70 м , но умножьте на , чтобы получить
.
Содержание
- — Как находить периметр основания?
- — Что такое периметр параллелограмма?
- — Как найти периметр квадрата 4 класс формула?
- — Как найти площадь и периметр квадрата 4 класс?
- — Как найти Апофему в пирамиде?
Как находить периметр основания?
Sбок = Pl; V = Sосн · H , где Sбок — площадь боковой поверхности призмы, P — периметр перпендикулярного сечения, l — длина бокового ребра, V — объем, Sосн — площадь основания, H — высота призмы.
Что такое периметр параллелограмма?
1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b). См. также: Программа для расчета периметра параллелограмма.
Как найти периметр квадрата 4 класс формула?
О чем эта статья: Основные определения Формула нахождения периметра квадрата Если известна длина стороны
…
Как решаем:
- Воспользуемся формулой P = 4 * a;
- Тогда a = P : 4;
- a = 20 : 4 = 5 см;
- Воспользуемся формулой S = a * a;
- Значит S = 5 * 5;
Как найти площадь и периметр квадрата 4 класс?
Площадь квадрата равна квадрату его стороны. Периметр квадрата равен сумме его четырех сторон.
Как найти Апофему в пирамиде?
Пирамида, основанием которой является правильный многоугольник, а вершина которой проецируется в центр основания, называется правильной пирамидой. Боковые грани правильной пирамиды — равные равнобедренные треугольники. Высота боковой грани правильной пирамиды называется апофемой.
Интересные материалы:
Как обновить цвет кирпича?
Как определить цвет древесины?
Как определить цвет кожи для выбора тональных средств?
Как определить возраст мореного дуба по цвету?
Как определиться с цветом натяжного потолка?
Как определится с цветом пола на кухне?
Как оранжевый цвет влияет на психику?
Как освежить цвет обивки дивана?
Как освежить цвет тротуарной плитки?
Как по другому называется розовый цвет?
ЕГЭ формулы, шпаргалки — Элементарная геометрия. Пирамида.
Площадь боковой поверхности правильной пирамиды:
,
где Р — периметр основания, h — апофема.
,
Площадь боковой поверхности правильной усеченной пирамиды:
,
,
Полный список всех формул, шпаргалок для ЕГЭ по математике тут: ЕГЭ математика — формулы, шпаргалки.
Пирамида
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
Виды пирамид
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Пирамида
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
- боковые рёбра правильной пирамиды равны;
- в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
- в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна Пи, а каждый из них соответственно Пи/n, где n — количество сторон многоугольника основания;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

 – 288 с.: ил.
– 288 с.: ил. Боковое ребро DA перпендикулярно плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.
Боковое ребро DA перпендикулярно плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.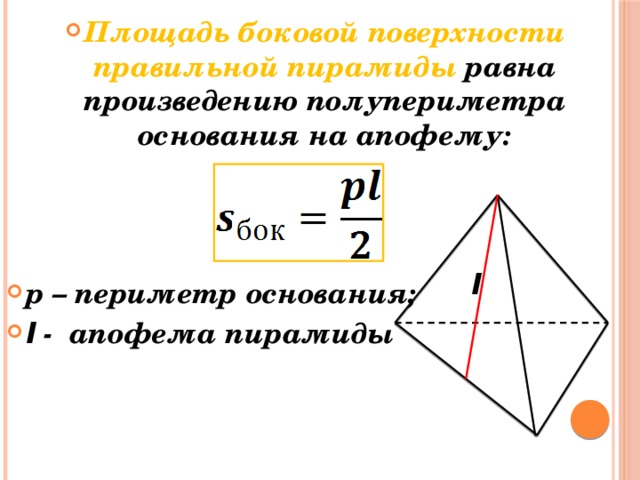
 )
)