Как найти периметр квадрата внутри треугольника

Независимое внешнее тестирование по математике ЗНО 2013

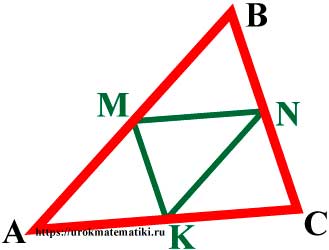
В треугольник ABC вписан квадрат KLMN (см.рисунок). Высота этого треугольника, опущенная на сторону АС, равна 6 см. Найдите периметр квадрата, если АС = 10 см.

Варианты ответа:
А: 7,5 см Б: 12,5 см В: 17,5 см Г: 15 см Д: 20 см

Решение
Пусть сторона квадрата равна x. Рассмотрим подобные треугольники АВС и KBL. Запишем пропорцию для их высот и оснований.

Вот здесь можно сэкономить себе несколько драгоценных секунд, которые затем пригодятся для решения других задач.

Надо ли нам делить 60 на 16, чтобы получить х? Нет, т.к. в условии нас спрашивают про периметр квадрата. Периметр его равен 4х. Так что разделив левую и правую часть уравнения на 4, сразу получим периметр:
4x = 15

Как вписать квадрат в треугольник?

Отсюда, как найти площадь совмещенных фигур? Для вычисления площади составной фигуры необходимо разделить фигуру на прямоугольники, треугольники или другие формы, которые вы можете найти, а затем снова сложить области. Возможно, вам придется рассчитать недостающую длину, прежде чем определять площадь некоторых фигур.

Можно ли возвести треугольник? можно возвести в квадрат путем возведения прямоугольника в квадрат. Общий многоугольник можно рассматривать, рисуя диагонали, возводя в квадрат составляющие треугольники, а затем объединяя квадраты вместе, используя теорему Пифагора.

Похожие страницы:Блог

Какие есть 3 вида налогов?

Как найти среднюю точку между двумя точками?

Как вы делаете кадровые прогнозы?

Как найти начальную скорость, зная только время?

Дополнительно Могут ли 2 треугольника составить квадрат? Важной особенностью, которую следует отметить в каждом из этих представлений, является то, что два «последовательных» треугольных массива объединяются, чтобы сделать квадрат, длина стороны которого соответствует большему треугольнику.

Сколько квадратных углов у треугольника? Все треугольники имеют три угла, но только некоторые треугольники зеленые. Все треугольники замкнуты, но только некоторые треугольники перевернуты. У всех прямоугольников четыре прямые стороны, но только некоторые прямоугольники красные. Все прямоугольники имеют четыре квадратных угла, но только некоторые прямоугольники высокие и узкие.

Как найти площадь составного треугольника?

Как найти площадь неправильного квадрата? Как пользоваться калькулятором неровной площади?

1. Шаг 1: Измерьте все стороны площади одной единицей (футы, метры, дюймы или любые другие).
2. Шаг 2: Введите длину горизонтальных сторон в поля «Длина 1» и «Длина 2», а ширину вертикальных сторон в поля «Ширина 1» и «Ширина 2».
3. Шаг 3: Нажмите кнопку расчета. …
4. Наша формула: Площадь = b × h.

Что такое комбинированные фигуры? Комбинированная фигура это форма, представляющая собой комбинацию нескольких более простых форм. Чтобы найти периметр, мы складываем все внешние стороны нашей фигуры. Чтобы найти площадь, мы делим нашу фигуру на ее простые фигуры, вычисляем площади этих фигур по отдельности, а затем складываем эти площади, чтобы получить общую сумму.

Как сделать треугольник из квадратных блоков?

А также Могут ли 4 равнобедренных треугольника составить квадрат? Я хорошо, квадрат всегда состоит из четырех равнобедренных треугольных прямоугольников и конгруэнтны, так что подходит идеально.

Какие виды треугольников составляют квадрат?

Меградж Шах

• Меградж Шах. Ответ получен: 5 сентября 2005 г.
• 2 равносторонних треугольника с прил hyp составят квадрат. никакая другая комбинация треугольников не подходит для образования квадрата.

Что делает квадрат квадратом? Свойства квадрата:

У квадрата 4 стороны и 4 вершины. Все стороны квадрата равны по длине. Все внутренние углы равны и прямые. Сумма всех внутренних углов равна 360°.

Все ли треугольники имеют прямые углы?

Однако, каждый треугольник может иметь либо угол внутри (1 балл) или две вершины на углах (1 балл) максимум 1 балл. Три треугольника получают не более 3 угловых очков мощности, чего недостаточно для покрытия квадрата.

Есть ли у треугольника углы?

Треугольник – это фигура, образованная при пересечении трех прямых линий. Все треугольники имеют три стороны и три угла (углы). Точка, в которой встречаются две стороны треугольника, называется вершиной.

Что такое прямые углы? Квадрат – это фигура с четырьмя сторонами одинаковой длины и четыре угла что все прямые углы.

Какова формула составной формы? Используя формулу площади составной фигуры, Площадь составной форма = площадь прямоугольника + площадь квадрата. ⇒ Площадь составной фигуры = 14+9 = 23 квадратных дюйма.

Какова формула составной фигуры?

Как вычислить площадь? для краткости), определите длину и ширину области, с которой вы работаете, измеренную в футах. Умножьте длину на ширину, и вы получите квадратные метры. Вот основная формула, которой вы можете следовать: Длина (в футах) x ширина (в футах) = площадь в кв.

Как найти площадь неправильного треугольника?

Измерьте основание и высоту треугольника (от основания до высшей точки треугольника) в футах. Умножьте эти два числа. Затем разделите сумму на два, и вы будет иметь квадратные метры треугольника.

Как найти площадь неправильной формы с 4 сторонами без угла? 1 × Диаг.. 2)/2 или A = (d₁ × д₂)/2. Пример: Четырехсторонняя фигура имеет две смежные стороны длиной 4 метра. Вы можете найти площадь этого квадрата, умножив его основание на высоту: 4 × 4 = 16 квадратных метров.

Как найти площадь 4-х неравных сторон?

Площадь любого неправильного четырехугольника можно вычислить. разделив его на треугольники. Пример. Найдите площадь четырехугольника ABCD, стороны которого равны 9 м, 40 м, 28 м и 15 м соответственно, а угол между первыми двумя сторонами является прямым. Площадь четырехугольника ABCD = (180 + 126) = 306 квадратных метров.

Как найти периметр квадрата и треугольника вместе взятых?

Является ли квадрат составной фигурой?

Составная форма – это 2D форма который состоит из комбинации других основных 2D-форм и многоугольников. Эти формы включают квадраты, прямоугольники, треугольники, круги и многое другое!

Что такое составная форма? Составная форма или составная фигура двухмерная фигура, состоящая из основных двухмерных фигур такие как треугольники, прямоугольники, круги, полукруги и т. д.

Треугольник

Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Типы треугольников

По величине углов

Остроугольный треугольник

— все углы треугольника острые.

Тупоугольный треугольник

— один из углов треугольника тупой (больше 90°).

Прямоугольный треугольник

— один из углов треугольника прямой (равен 90°).

По числу равных сторон

Разносторонний треугольник

— все три стороны не равны.

Равнобедренный треугольник

— две стороны равны.

Равносторонний (правильный) треугольник

— все три стороны равны.

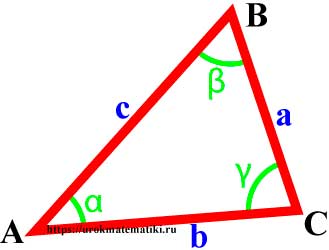
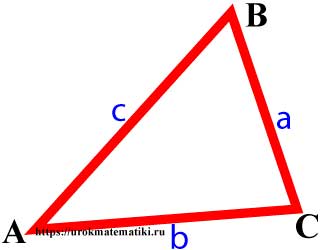
Вершины, углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы

• если α > β , тогда a > b
• если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны

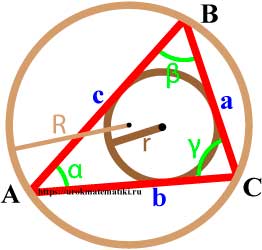
Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a sin α = b sin β = c sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 b c · cos α
b 2 = a 2 + c 2 — 2 a c · cos β
c 2 = a 2 + b 2 — 2 a b · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a = 2 3 2 m b 2 + m c 2 — m a 2

b = 2 3 2 m a 2 + m c 2 — m b 2

c = 2 3 2 m a 2 + m b 2 — m c 2

Медианы треугольника

Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника

1. Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.

S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m a = 1 2 2 b 2 + 2 c 2 — a 2

m b = 1 2 2 a 2 + 2 c 2 — b 2

m c = 1 2 2 a 2 + 2 b 2 — c 2

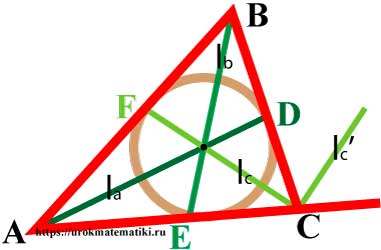
Биссектрисы треугольника

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника

1. Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.

Угол между l c и l c ‘ = 90°

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны

l a = 2 b c p p — a b + c

l b = 2 a c p p — b a + c

l c = 2 a b p p — c a + b

где p = a + b + c 2 — полупериметр треугольника.

Формулы биссектрис треугольника через две стороны и угол

l a = 2 b c cos α 2 b + c

l b = 2 a c cos β 2 a + c

l c = 2 a b cos γ 2 a + b

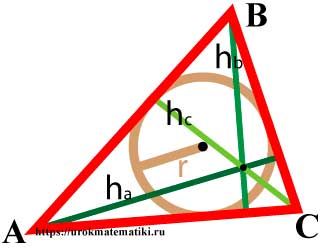
Высоты треугольника

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться:

• внутри треугольника — для остроугольного треугольника;
• совпадать с его стороной — для катета прямоугольного треугольника;
• проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

1. Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Формулы высот треугольника

Формулы высот треугольника через сторону и угол

h a = b sin γ = c sin β

h b = c sin α = a sin γ

h c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

Свойства окружности вписанной в треугольник

• Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
• В любой треугольник можно вписать окружность, и только одну.

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру

Радиус вписанной в треугольник окружности через три стороны

Формулы высот треугольника через две стороны и радиус описанной окружности

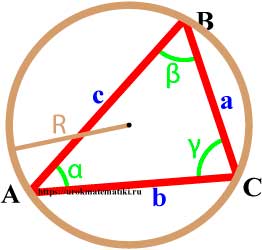
Окружность описанная вокруг треугольника

Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

Свойства окружности описанной вокруг треугольника

• Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
• Вокруг любого треугольника можно описать окружность, и только одну.

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь

Радиус описанной окружности через площадь и три угла

Радиус описанной окружности через сторону и противоположный угол (теорема синусов)

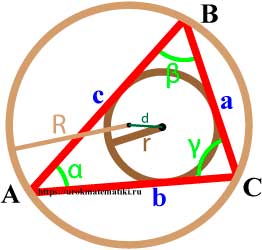
Связь между вписанной и описанной окружностями треугольника

Формулы радиуса окружности описанной вокруг треугольника

Если d — расстояние между центрами вписанной и описанной окружностей, то

d 2 = R 2 — 2 R r

Радиус описанной окружности через площадь и три угла

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника

• Любой треугольник имеет три средних линии.
• Средняя линия треугольника параллельна основанию и равна его половине.
  MN = 1 2 AC ; KN = 1 2 AB ; KM = 1 2 BC

Признаки

Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

S = 1 2 a · h a ,
S = 1 2 b · h b ,
S = 1 2 c · h c ,

где a, b, c — стороны треугольника,
h_a, h_b, h_c — высоты, проведенные к сторонам a, b, c треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p — a p — b p — c ,

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,
S = 1 2 b · c · sin α ,
S = 1 2 a · c · sin β ,

где a, b, c — стороны треугольника,
γ — угол между сторонами a и b ,
α — угол между сторонами b и c ,
β — угол между сторонами a и c .

Формула площади треугольника по трем сторонам и радиусу описанной окружности

S = a · b · c 4 R ,

a, b, c — стороны треугольника,
R — радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2

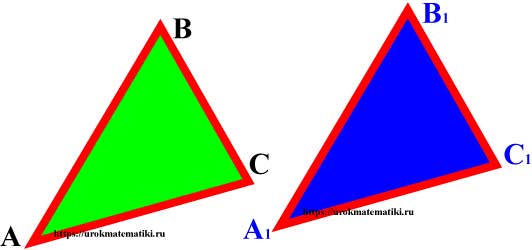
Равенство треугольников

Определение

Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства

У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).

Признаки равенства треугольников

По двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

Определение

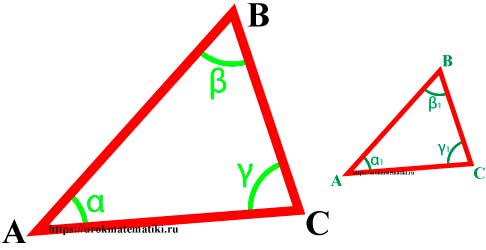
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

∆MNK => α = α 1 , β = β 1 , γ = γ 1 и AB MN = BC NK = AC MK = k

где k — коэффициент подобия.

Признаки подобия треугольников

1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
3. Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

S ∆АВС S ∆MNK = k 2

Прямоугольные треугольники

Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).

Свойства прямоугольного треугольника

Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∠ 1 + ∠ 2 = 90° .

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).

Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.

Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.

Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия: