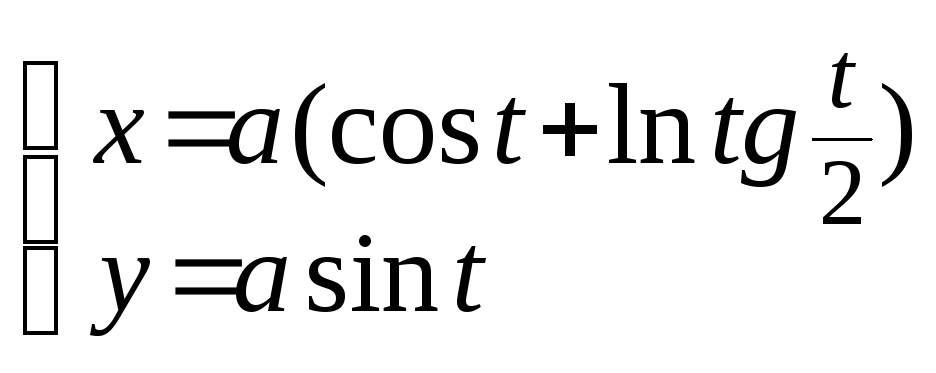Найти площадь и периметр фигуры, ограниченной следующими линиями.
Пример 1:
Найти площадь и периметр фигуры, ограниченной следующими линиями:
Решение от преподавателя:
Фигура имеет вид:
Периметр фигуры
Площадь
Пример 2:
Найдем площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах:
Решение от преподавателя:
Вычислим площадь:
Тогда подставим наши значения:
Проведем преобразования:
Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Как найти периметр фигуры
В задачах по геометрии часто требуется найти периметр фигуры. Периметром фигуры называется длина ограничивающей ее линии. Можно, конечно, просто измерить длину этой линии. Однако, результаты таких измерений могут оказаться недостаточно точными. Кроме того, измерение длины кривой линии – довольно-таки трудный процесс. Поэтому на практике и при решении геометрических задач обычно используют специальные формулы.
Чтобы найти периметр фигуры, ограниченной ломаной линией, сложите длины всех составляющих ее отрезков. Если длины отрезков неизвестны, измерьте их с помощью циркуля и линейки. Если фигура имеет сравнительно большие размеры, воспользуйтесь рулеткой. Единицей измерения периметра будут служить те же единицы, в которых заданы (измерялись) длины составляющих отрезков. Если единицы измерения разные, то их необходимо привести к одному виду.Например, если земельный участок имеет треугольную форму с длинами сторон 10, 20 и 30 метров, соответственно, то его периметр составит: 10 + 20 + 30 (м).
Для нахождения периметра простых геометрических фигур, воспользуйтесь специальными формулами.Чтобы найти периметр ромба (в частности, квадрата), умножьте длину его стороны на четыре. То есть, воспользуйтесь следующими формулами:П(ромб) = П(квадрат) = 4 * с,
где с – длина стороны ромба (квадрата), П – его периметр.
Для нахождения периметра параллелограмма (в частности, прямоугольника), сложите его длину и ширину и умножьте на два (под длиной и шириной подразумеваются длины двух смежных сторон). Нагляднее, это можно записать в следующем виде:П(параллелограмм) = П(прямоугольник) = 2 * (д + ш), где:
д и ш – длина и ширина параллелограмма (прямоугольника), соответственно.
Чтобы найти периметр круга, вычислите длину ограничивающей его окружности. Для этого воспользуйтесь классической формулой:П(круг) = π * Д или
П(круг) = 2 * π * Р,
где: Д – диаметр круга, Р – радиус круга,π – число «пи», примерно равное 3,14.
Если известна длина диагонали квадрата, то для нахождения его периметра используйте следующую формулу:П(квадрат) = 2√2 * д,где д – длина диагонали квадрата.
Периметр квадрата можно рассчитать, используя информацию о его площади. Для этого воспользуйтесь следующим правилом:П(квадрат) = 4 * √Sкв,где Sкв – площадь квадрата.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||||
|---|---|---|---|---|---|
|
Заголовок сообщения: Найти периметр фигуры
|
|||||
|
Найти периметр фигуры ограниченной кривой y=lnx , касательной к ней в т.х=е и осью ОХ.
|
||||
| Вернуться к началу |
|
||||
|
Kitamo |
Заголовок сообщения: Re: Найти периметр фигуры
|
|
Avgust писал(а): Прямолинейные участки — по знаниям средней школы, а криволинейный — при помощи определенного интеграла. Но ведь определенный интеграл это площадь криволинейной трапеции?
|
|
| Вернуться к началу |
|
|
Kitamo |
Заголовок сообщения: Re: Найти периметр фигуры
|
|
По формуле
|
|
| Вернуться к началу |
|
|
Kitamo |
Заголовок сообщения: Re: Найти периметр фигуры
|
|
А дальше не знаю что делать и вообще то ли делаю(Я совсем профан в интегралах
|
|
| Вернуться к началу |
|
|
Kitamo |
Заголовок сообщения: Re: Найти периметр фигуры
|
|
Как то так…а дальше что делать?
|
|
| Вернуться к началу |
|
|
Avgust |
Заголовок сообщения: Re: Найти периметр фигуры
|
|
Это трудный путь. Проще сделать первую замену [math]1+x^2=t^2[/math] а потом замену [math]sin(z)=t[/math] Тогда легко придете к ответу: [math]sqrt {1+{x}^{2}}+frac 12,ln left| {frac {sqrt {1+{x}^{2}}-1}{sqrt {1+{x}^{2}}+1}} right | +C[/math]
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Чтобы периметр каждой фигуры был равен периметру квадрата
в форуме Размышления по поводу и без |
Xenia1996 |
0 |
208 |
15 окт 2017, 23:49 |
|
Найти периметр треугольника
в форуме Геометрия |
Falenhero |
5 |
160 |
05 фев 2021, 12:44 |
|
Найти периметр треугольник
в форуме Геометрия |
dikarka2004 |
5 |
169 |
17 ноя 2021, 06:11 |
|
Найти периметр треугольника
в форуме Геометрия |
sfanter |
2 |
375 |
06 июл 2014, 12:21 |
|
Найти периметр ромба
в форуме Геометрия |
Houston |
2 |
777 |
15 янв 2014, 19:16 |
|
Найти периметр треугольника
в форуме Геометрия |
gail-ul |
10 |
504 |
30 ноя 2016, 22:24 |
|
Найти периметр треугольника
в форуме Геометрия |
Woxa999 |
3 |
696 |
09 ноя 2014, 17:27 |
|
Найти периметр треугольника
в форуме Геометрия |
dikarka2004 |
3 |
127 |
31 мар 2022, 09:56 |
|
Задача найти периметр
в форуме Геометрия |
Bate777 |
13 |
494 |
03 фев 2019, 20:41 |
|
Найти периметр прямоугольника
в форуме Геометрия |
Dexter333 |
11 |
848 |
11 фев 2014, 16:38 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
You should upgrade or use an alternative browser.
-
Forums
-
Mathematics
-
Calculus
Calculating the perimeter of a region using integrals
-
Thread starter
esmeco -
Start date
Feb 5, 2007 -
-
Tags -
Integrals
Perimeter
-
- Feb 5, 2007
- #1
Any help on this is really appreciated!Thanks in advance!
Answers and Replies
- Feb 5, 2007
-
- #2
ds2=dx2+dy2.
In practice, you would use:
ds=(1+(dy/dx)2)1/2dx
- Feb 5, 2007
- #3
[tex]ds= sqrt{left(frac{dx}{dt}right)+ left(frac{dy}{dt}right)^2}ds[/tex]
If the perimeter is given by two or more different formula (as a region defined to be between two curves) you will need to integrate each separately and then add.
- Feb 5, 2007
-
- #4
- Feb 6, 2007
- #5
We add all those tiny lengths up to get the entire curve’s length.
- Feb 6, 2007
- #6
For the area, we cut up the region into tiny rectangles yes? well the integral basically makes it perfectly accurate by making lots and lots of rectanles. For that to happen, the base has to be smaller. When its really small, we call it dx. a small change in x. a small change in height would then be dy.
if we took those small changes in x and y, and applied pythagoras to them to get the straight line that connects them. That imitates the perimeter abit. Then we integrate it to sum all of the small ones. 
- Feb 6, 2007
- #7
ds=sqrt(2^2 + 2^2)=sqrt8
Is this correct?But what do I do now with the hipothenus value?
- Feb 7, 2007
- #8
if [tex]y=sqrt{x+2}[/tex]. Try drawing the graph. Then zoom in. It gets abit straighter yea? Then in even more, it’ll look even more straight. Since a tangent straight line then becomes a good approximation of that part, we make a straight line that hugs the curve. To do that, we take the lines vertical height, and horizontal height. From those 2, and Pythagoras Theorem, we get the length of the line that hugs the curve. The tangent will vary in different places, and this method of doing this is very long, taxing and sort of in accurate. With Integral calculus, we can do this process perfectly accurately and very quickly.
But you haven’t done Differential Calculus yet, so your at least a good few months off this.
- Feb 7, 2007
- #9
[tex]int^b_a sqrt{1+ (y’)^2} dx[/tex]. Thats the perimeter of the function y, from b to a. I tried use prime notation rather than Leibniz, but that’s hard to do with Integrals lol.
From your other forums, it seems you haven’t encountered integrals, but rather only primitives.
- Feb 7, 2007
- #10
Suggested for: Calculating the perimeter of a region using integrals
- Apr 30, 2022
- Feb 10, 2023
- May 6, 2022
- May 23, 2022
- Oct 31, 2021
- Jul 13, 2021
- Dec 15, 2020
- Oct 11, 2021
- Nov 1, 2020
-
Forums
-
Mathematics
-
Calculus
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
6
Добавлен:
04.06.2015
Размер:
1.22 Mб
Скачать
-
Построить фигуру,
ограниченную линиями, и найти ее площадь:
а)
,
у
= 0, у
= 5 –х;
б)
вне r
= a,
а
> 0.
-
а) Найти длину
дуги кривой у
= ех
между точками (0, 1) и (1, е).
Указание: в качестве независимой
переменной взятьу.
б) Найти длину дуги кардиоиды
.
-
Найти объем тела,
полученного при вращении вокруг оси
ОХ фигуры, ограниченной линиями у
= tgx,
y
= ctgx,
x
=
.
-
Скорость тела,
брошенного вертикально вверх с начальной
скоростью v0,
с учетом сопротивления воздуха дается
формулой
,
гдеt
– протекшее время, g
– ускорение свободного падения, С
– постоянная. Найти высоту поднятия
тела. -
Вычислить силу
давления жидкости с плотностью
на вертикальный эллипс с осями 2а
и 2b,
центр которого погружен в жидкость на
уровень h
(h
b),
причем большая ось 2а
эллипса параллельна поверхности
жидкости. -
Тяжелая цепь
длиной 100 м поднимается, навиваясь на
ворот. Найдите работу силы тяжести при
поднятии цепи, пренебрегая размерами
ворота, если погонный метр цепи весит
40 кг.
Дополнительные задачи
-
Вычислить интеграл
,
рассматривая его как предел интегральной
суммы. -
Оценить интеграл
.
-
Исходя из
геометрического смысла определенного
интеграла, найти:
а)
;
б).
-
Исследовать
сходимость интеграла.
-
Вычислить
.
-
Найти площадь
петли декартова листа
,
0
t
< +. -
Доказать,
что дуги линийи
,
соответствующие одному и тому же
интервалу изменения параметраt,
имеют равные длины. -
/4б/
Фигура, ограниченная осью ОХ и одной
аркой циклоиды х
= а(t
– sint),y
= a(1
– cost),
вращается вокруг оси ОУ. Найти объем
тела вращения. -
Найти
массу стержня длины 100 см с переменной
плотностью (х)=.
ОТВЕТЫ. Часть 1. 1. а) нет; б) да; в) нет.
2.. 0 3. а)
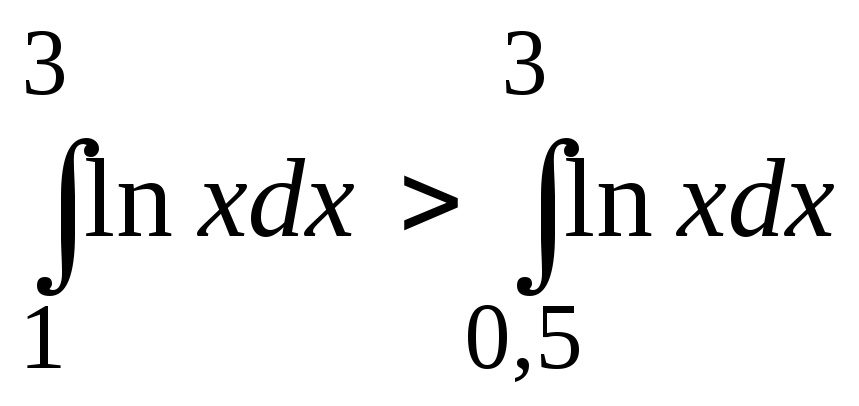
б).
4.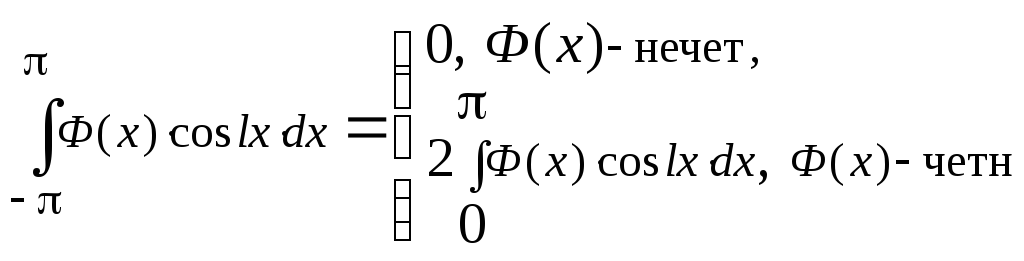
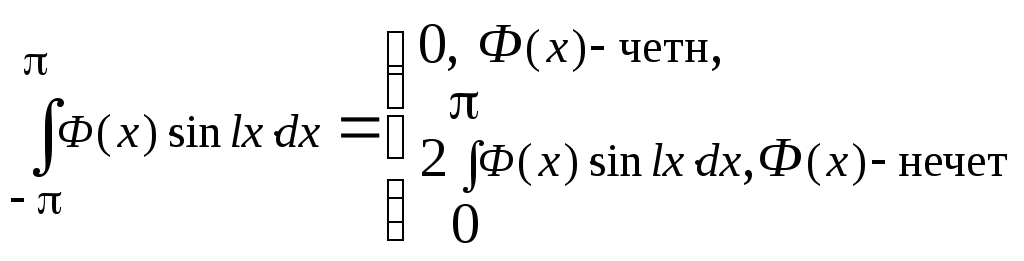
5. а)б) 0 в) 0,25 г)
д)(е–1–1)/3 е)ln2
ж)з)
6.
7.а) расходится б) 1–ln2
Часть 2. 1. а) 32/3 б)2. а)
б)6а3.
4.5.аbhgγ
6. –200000gкг.м.
Вариант 10 Часть 1
-
Используя
теорему существования определенного
интеграла, установить, существует ли
определенный интеграл от заданной
функции по указанному промежутку:
а)
g(x)
= (x+4)cos
x,
,
б),
в)у(х)
= х2
+ 3х,
(–;
1]
-
Используя
одно из свойств определенного
интеграла, упростить вычисление
интеграла
.
-
Не вычисляя,
определить, какой из интегралов
больше:
а)
или
;
б)
или
.
Ответ обосновать.
4. Чему равны
и
,
если f(х)
— четная функция; нечетная функция?
5. Вычислить: а)
,
б)
,
в)
,
г)
,
д),
е),
ж)
,
з)
.
6. Вычислить
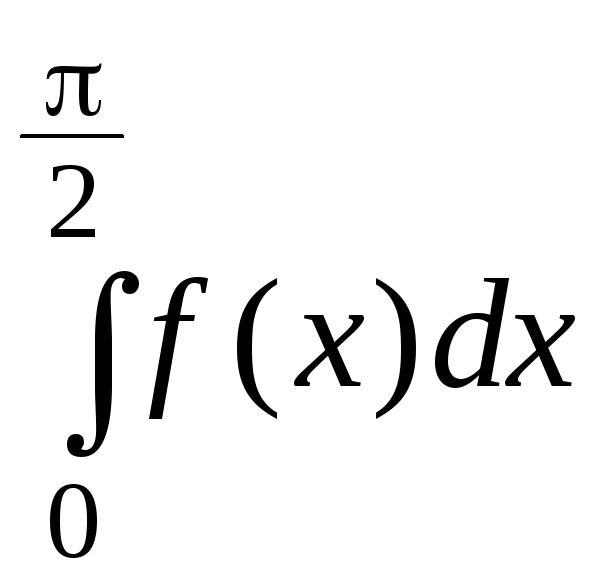
если
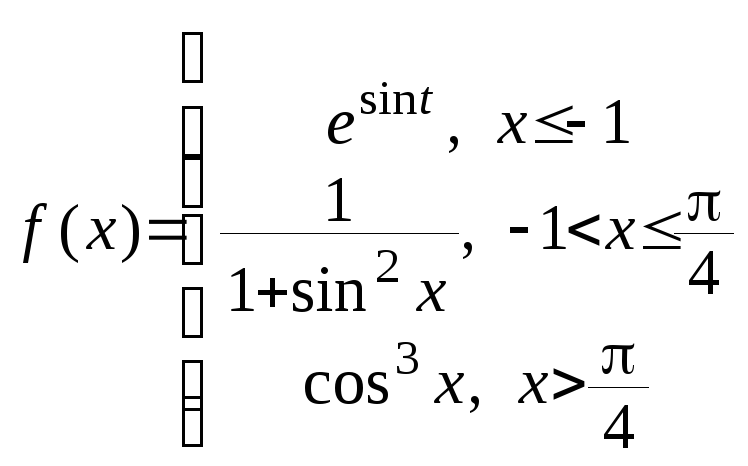
7. Вычислить
интегралы, или установить их расходимость:
а)
,
б)
.
Часть 2
-
Построить фигуру,
ограниченную линиями, и найти ее площадь:
а)
б)
,
r
= a,
.
2. а) Найти периметр
фигуры, ограниченной линиями:
Указание: в качестве независимой
переменной взятьу.
б) Найти длину
дуги трактрисы:
от точки (0; а)
до точки (b;
с).
-
Найти объем тела,
полученного вращением вокруг оси OY
фигуры, ограниченной линиями
(x,
y
0) и y
= 3. -
Ракетный снаряд
поднимается вертикально вверх. Считая,
что при постоянной силе тяжести ускорение
ракеты за счет уменьшения ее веса растет
по закону
,
найти скорость ракеты в момент времениt1,
если ее начальная скорость равна нулю. -
Найти силу давления
жидкости с плотностью ,
заполняющей круговой цилиндр, на его
боковые стенки, если радиус основания
цилиндра R,
высота Н. -
Какую работу
надо затратить, чтобы тело массы m
поднять с поверхности Земли, радиус
которой R,
на высоту h?
Чему равна эта работа, если тело удаляется
на бесконечность? (Сила, действующая
на тело массойm, равна,
гдеr— расстояние от
центра Земли; М — масса Земли,–
гравитационная постоянная).
Соседние файлы в папке FAIT1_1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

















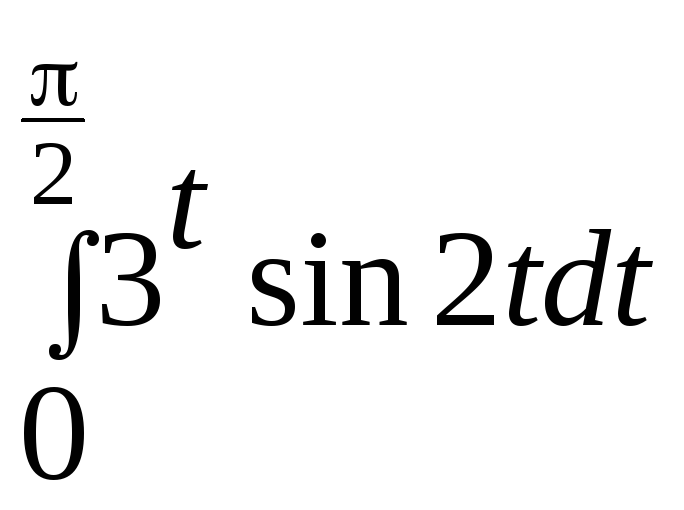 .
.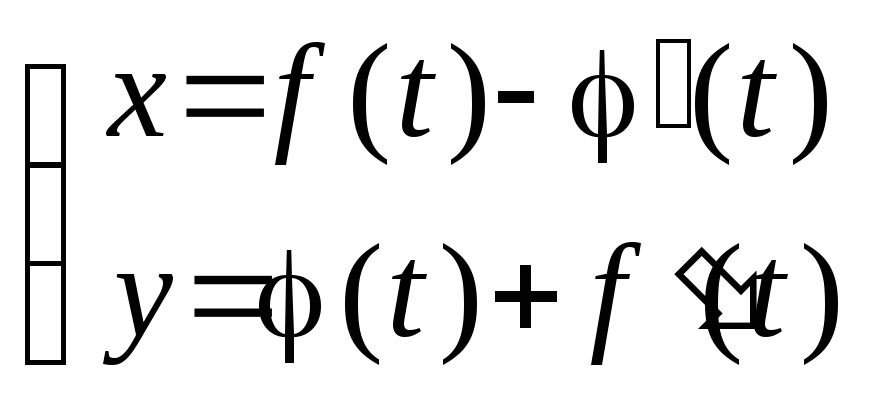 и
и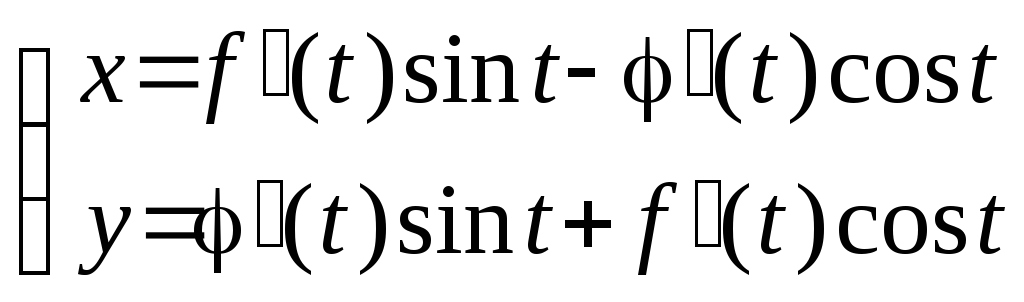 ,
,