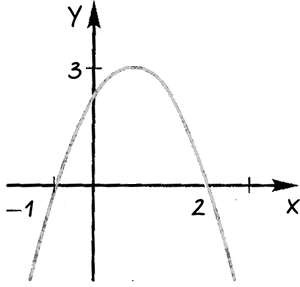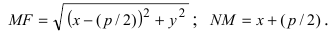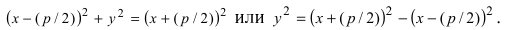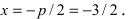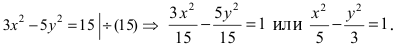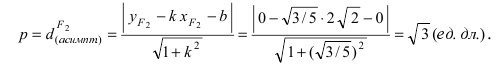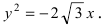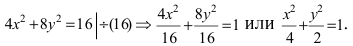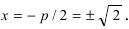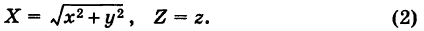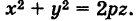В предыдущем уроке мы подробно разобрали,
как построить параболу.
В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Запомните!
Чтобы найти координаты точек нулей функции, нужно
в исходную функцию подставить вместо «y» число
ноль.
Рассмотрим задачу.
Найти нули квадратичной
функции «y = x2 − 3».
Подставим в исходную функцию вместо «y» ноль и решим полученное
квадратное уравнение.
0 = x2 − 3
x2 − 3 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
x1;2 = ±√3
Ответ: нули функции «y = x2 − 3» :
x1 = √3;
x2 = −√3 .
Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение
Запомните!
Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение,
нужно:
- вместо «y» подставить в функцию заданное числовое значение;
- решить полученное квадратное уравнение относительно «x».
Рассмотрим задачу.
При каких значениях «x» функция
«y = x2 − x − 3» принимает значение
«−3».
Подставим в исходную функцию
«y = x2 − x − 3» вместо «y = −3» и
найдем «x».
y = x2 − x − 3
−3 = x2 − x − 3
x2 − x − 3 = −3
x2 − x − 3 + 3 = 0
x2 − x = 0
x1;2 =
| 1 ± √12 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = 0 |
Ответ: при «x = 0» и
«x = 1» функция «y = x2 − x − 3»
принимает значение «y = −3».
Как найти координаты точек пересечения параболы и прямой
Запомните!
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся «x»);
- решить полученное уравнение относительно «x»;
- подставить полученные числовые значения «x»
в любую из функций и найти координаты точек по оси «Оy».
Рассмотрим задачу.
Найти координаты точек пересечения параболы «y = x2»
и прямой «y = 3 − 2x».
Приравняем правые части функций и решим
полученное уравнение относительно «x».
x2 = 3 − 2x
x2 − 3 + 2x = 0
x2 + 2x − 3 = 0
x1;2 =
| −2 ± √22 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = −3 |
Теперь подставим в любую из заданных функций (например, в
«y = 3 − 2x») полученные
числовые значения «x», чтобы найти координаты
«y» точек пересечения.
1) x = −3
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.
2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Ответ: точки пересечения параболы
«y = x2»
и прямой «y = 3 − 2x»:
(·) A (−3; 9) и
(·) B (1; 1).
Как определить, принадлежит ли точка графику функции параболы
Запомните!
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Рассмотрим задачу:
Не строя графика функции «y = x2», определить, какие точки принадлежат ему:
(·) А(2; 6),
(·) B(−1; 1).
Подставим в функцию
«y = x2»
координаты точки (·) А(2; 6).
y = x2
6 = 22
6 = 4
(неверно)
Значит, точка (·) А(2; 6)
не принадлежит графику функции
«y = x2».
Подставим в функцию
«y = x2»
координаты точки (·) B(−1; 1).
y = x2
1 = (−)12
1 = 1
(верно)
Значит, точка (·) B(−1; 1)
принадлежит графику функции
«y = x2».
Как найти точки пересечения параболы с осями координат
Рассмотрим задачу
Найти координаты точек пересечения параболы
«y = x2 −3x + 2» с осями координат.
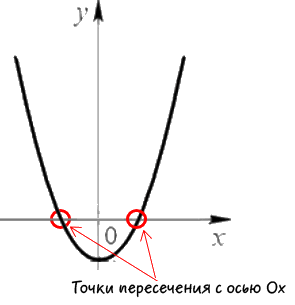
Сначала определим точки пересечения функции с осью «Ox».
На графике функции эти точки выглядят так:
Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox»
равна нулю, поэтому подставим «y = 0» в
исходную функцию «y = x2 −3x + 2»
и найдем их координаты по оси «Ox».
0 = x2 −3x + 2
x2 −3x + 2 = 0
x1;2 =
| 3 ± √32 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 2 | x2 = 1 |
Запишем координаты точек пересечения графика с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
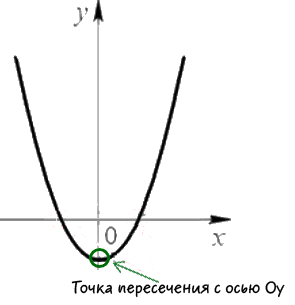
Теперь найдем координаты точки пересечения с осью «Oy».
Как видно на рисунке выше, координата «x»
точки пересечения с осью «Oy» равна нулю.
Подставим «x = 0»
в исходную функцию
«y = x2 −3x + 2»
и найдем координату точки по оси
«Oy».
y(0) = 02 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).
Как определить при каких значениях x функция принимает
положительные или
отрицательные значения
Напоминаем, что когда в задании говорится «функция принимает
значения» — речь идет о
значениях«y».
Другими словами, необходимо ответить на вопрос: при каких значениях
«x», координата
«y» положительна или отрицательна.
Запомните!
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
- провести прямые через точки в местах, где график пересекает ось «Ox»;
- определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
- записать ответ для каждого промежутка относительно «x».
Рассмотрим задачу.
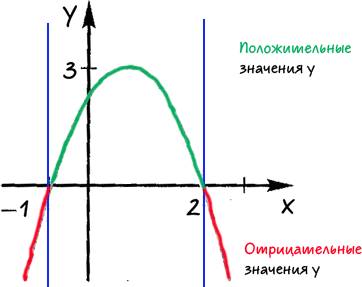
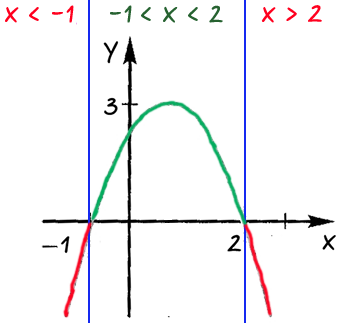
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения; 2) отрицательные значения.
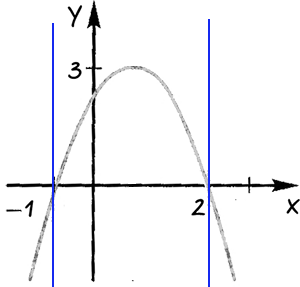
Проведем через точки, где график функции пересекает ось «Ox» прямые.
Определим области, где функция принимает отрицательные или положительные значения.
Подпишем над каждой полученной областью, какие значения принимает
«x» в каждой из выделенных областей.
Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при «−1 < x < 2» функция принимает
положительные значения.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
$$ ax^2+bx+c = a(x+ frac{b}{2a})^2-frac{D}{4a}, D = b^2-4ac $$
Мы получаем:
- ось симметрии $x = -frac{b}{2a}$
- вершину параболы на оси симметрии $(–frac{b}{2a}; -frac{D}{4a})$
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c).
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$, парабола имеет две точки пересечения с $x_1,2 = frac{-b pm sqrt{D}}{2a}$ на оси OX.
Если D = 0, парабола имеет одну точку пересечения $x_0 = -frac{b}{2a}$, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Точки пересечения параболы с осью OX
|
$a gt 0$ |
$a lt 0$ |
|
|
$D gt 0$ |
 |
 |
|
$x_(1,2) = frac{-b pm sqrt{D}}{2a}$ |
||
|
D = 0 |
 |
 |
|
$x_0 = -frac{b}{2a}$ |
||
|
$ D lt 0 $ |
 |
 |
|
${ varnothing }$-нет пересечений |
Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.
Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
$$ Ax^2+Bx+C = 0 $$
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
A = B = C = 0
$ a_1 = a_2, b_1 = b_2, $
$ c_1 = c_2 $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$
$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+bx+c_1$
$ y = ax^2+bx+c_2 $
У них общая ось симметрии
$ x = -frac{b}{2a}$, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет
$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c$
$ y = ax^2+b_2 x+c $
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Одна точка пересечения
(0;c)
$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c_1$
$ y = ax^2+b_2 x+c_2 $
Абсцисса точки пересечения
$ x = — frac{C}{B} = -frac{c_1-c_2}{b_1-b_2}$
Одна точка пересечения (касание)
$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c$
$ y = a_2 x^2+bx+c $
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)
$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c_1$
$ y = a_2 x^2+bx+c_2 $
Не пересекаются, если
$- frac{c_1-c_2}{a_1-a_2} lt 0 $
Две точки пересечения
Если
$- frac{c_1-c_2}{a_1-a_2} gt 0 $
Пересекаются в двух точках
$$ x_{1,2} = pm sqrt{-frac{c_1-c_2}{a_1-a_2}} $$
Две точки пересечения
$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
$ x_1 = 0 $
$$x_2 = -frac{b_1-b_2}{a_1-a_2}$$
Две точки пересечения,
одна из которых (0;c)
$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Все параметры парабол разные
Ищем дискриминант:
$$ D = B^2-4AC $$
Если $D gt 0$
Две точки пересечения
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} $$
Две точки пересечения
Если D = 0
Одна точка пересечения (касание)
$$ x_0 = -frac{B}{2A} $$
Одна точка пересечения
(касание)
Если $D lt 0$
Точек пересечения нет
Точек пересечения нет
Внимание!
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
$а) y = 3x^2+2x-1$
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -1end{array} right.}$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{3} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ — две точки пересечения
$б) y = -4x^2-3x+1$
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{4} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ — две точки пересечения
$в) y = 5x^2-2x+1$
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ 5x^2-2x+1 = 0 $$
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
$ г) y = -x^2+4x-4 $
Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -4end{array} right.}$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow {left{ begin{array}{c} x = 2 \ y = 0 end{array} right.}$$ — одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
По условию
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1
$$x_1 = 0, x_2 = -frac{B}{A} = -2$$
$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x+1 end{array} right.} Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x_1 = 0 \ y_1 = 1end{array} right.} \ {left{ begin{array}{c} x_2 = -2 \ y_2 = -1 end{array} right.} end{array} right.$$
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$
Например, k = 4
$$ D = 4k = 16 = 4^2 $$
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} = frac{-2 pm 4}{2} = left[ begin{array}{cc} x_1 = -3\ x_2 = 1 end{array} right. $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$
$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x end{array} right.} $$
$$ x_0 = frac{-B}{2A} = -1 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$
Например, k = -1
Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Координаты вершин:
$$ left( -frac{b_1}{2a_1}, — frac{D_1}{4a_1} right), left(- frac{b_2}{2a_2},- frac{D_2}{4a_2} right) $$
По условию:
$$ {left{ begin{array}{c} -frac{b_1}{2a_1} = -frac{b_2}{2a_2} \ -frac{D_1}{4a_1} = -frac{D_2}{4a_2} end{array} right.} Rightarrow {left{ begin{array}{c} frac{b_1}{a_1} = frac{b_2}{2a_2} \ frac{D_1}{a_1} = frac{D_2}{a_2} end{array} right.} $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac{x^2}{2}-3x+1$.
Координаты вершины:
$$ x_0 = — frac{b}{2a} = — frac{-3}{2 cdot frac{1}{2}} = 3, D = b^2-4ac = 3^2-4 cdot frac{1}{2} cdot 1 = 7 $$
$$ y_0 = — frac{D}{4a} = — frac{7}{4 cdot frac{1}{2}} = -3,5 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
$$ {left{ begin{array}{c} frac{b}{a} = frac{-3}{1/2} = -6 \ frac{D}{a} = frac{7}{1/2} = 14 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = 14a end{array} right.} $$
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ {left{ begin{array}{c} a = 1 \ b = -6a = -6 \ D = 14a = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ b^2-4ac = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ 36-4c = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ c = frac{36-14}{4} = 5,5 end{array} right.}$$
$$ y = x^2-6x+5,5 $$
$$ {left{ begin{array}{c} a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ c = — frac{1,44+2,8}{0,8} = -5,3 end{array} right.} $$
$$ y = -0,2x^2+1,2x-5,3 $$
Параболы
$$ y = frac{x^2}{2}-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)
Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac{x^2}{3}-2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac{b}{2a} = -frac{-2}{2 cdot frac{1}{3}} = 3, D = b^2-4ac = 2^2-4 cdot frac{1}{3} cdot 5 = — frac{8}{3} $$
$$ y_0 = — frac{D}{4a} = — frac{-8/3}{4 cdot 1/3} = 2 $$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
$$ {left{ begin{array}{c} frac{b}{a} = frac{-2}{1/3} = -6 \ frac{D}{a} = frac{-frac{8}{3}}{frac{1}{3}} = -8 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = b^2-4a underbrace{c}_{text{= 0 }} = b^2 = -8a end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ b^2 = -8a end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} b = frac{-8a}{-6a} = frac{4}{3} \ a = -frac{b}{6} = -frac{2}{9} end{array} right.} $$
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
$$ y = -frac{2}{9} x^2+ frac{4}{3} x $$
Кто может помочь, мальчики и девочки??
Найти координаты точек пересечения параболы с осями координат:
1) у= х2 + х — 12; 2) у = -х2 + 3х + 10;
3) у = -8х2 — 2х + 1; 4) у = 7х2 + 4х — 11;
1) у = 5х2 + х — 1; 6) у = 5х2 + 3х — 2;
7) у = 4х2 — 11х + 6; 
Содержание
- Как решать задачи на квадратичную функцию
- Как найти нули квадратичной функции
- Как найти при каких значениях « x » квадратичная функция принимает заданное числовое значение
- Как найти координаты точек пересечения параболы и прямой
- Как определить, принадлежит ли точка графику функции параболы
- Как найти точки пересечения параболы с осями координат
- Как определить при каких значениях x функция принимает положительные или отрицательные значения
- Взаимное расположение графиков квадратных трёхчленов
- Расположение графика квадратного трёхчлена относительно осей координат
- Точки пересечения двух парабол
- Примеры
Как решать задачи на квадратичную функцию
В предыдущем уроке мы подробно разобрали, как построить параболу. В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y » число ноль .
Найти нули квадратичной функции .
Подставим в исходную функцию вместо « y » ноль и решим полученное квадратное уравнение.
0 = x 2 − 3
x 2 − 3 = 0
x1;2 =
| 0 ± √ 0 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
x1;2 = ±√ 3
Как найти при каких значениях « x » квадратичная функция принимает заданное числовое значение
Чтобы найти при каких значениях « x » квадратичная функция принимает заданное числовое значение, нужно:
- вместо « y » подставить в функцию заданное числовое значение;
- решить полученное квадратное уравнение относительно « x ».
При каких значениях « x » функция принимает значение « −3 ».
Подставим в исходную функцию вместо « y = −3 » и найдем « x ».
−3 = x 2 − x − 3
x 2 − x − 3 = −3
x 2 − x − 3 + 3 = 0
x 2 − x = 0
x1;2 =
| 1 ± √ 1 2 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = 0 |
Ответ: при « x = 0 » и « x = 1 » функция « y = x 2 − x − 3 » принимает значение .
Как найти координаты точек пересечения параболы и прямой
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся « x »);
- решить полученное уравнение относительно « x »;
- подставить полученные числовые значения « x » в любую из функций и найти координаты точек по оси « Оy ».
Найти координаты точек пересечения параболы « y = x 2 » и прямой « y = 3 − 2x ».
Приравняем правые части функций и решим полученное уравнение относительно « x ».
x 2 = 3 − 2x
x 2 − 3 + 2x = 0
x 2 + 2x − 3 = 0
x1;2 =
| 2 ± √ 2 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 3 | x2 = −1 |
Теперь подставим в любую из заданных функций (например, в полученные числовые значения « x », чтобы найти координаты « y » точек пересечения.
1) x = 3
y = 3 − 2x
y(3) = 3 − 2 · 3 = 3 − 6 = −3
(·) A (3; −3) — первая точка пересечения.
2) x = −1
y = 3 − 2x
y(−1) = 3 − 2 · (−1) = 3 + 2 = 5
(·) B (−1; 5) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Ответ: точки пересечения параболы и прямой
(·) A (3; −3) и (·) B (−1; 5) .
Как определить, принадлежит ли точка графику функции параболы
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси « Ox » вместо « x », а координату по оси « Oy » вместо « y ») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка не принадлежит графику функции.
Не строя графика функции « y = x 2 », определить, какие точки принадлежат ему: (·) А(2; 6) , .
Подставим в функцию « y = x 2 » координаты точки (·) А(2; 6) .
Значит, точка (·) А(2; 6) не принадлежит графику функции .
Подставим в функцию « y = x 2 » координаты точки (·) B(−1; 1) .
Значит, точка (·) B(−1; 1) принадлежит графику функции .
Как найти точки пересечения параболы с осями координат
Найти координаты точек пересечения параболы с осями координат.
Сначала определим точки пересечения функции с осью « Ox ». На графике функции эти точки выглядят так:
Как видно на рисунке выше, координата « y » точек пересечения с осью « Ox » равна нулю, поэтому подставим « y = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем их координаты по оси « Ox ».
0 = x 2 −3x + 2
x 2 −3x + 2 = 0
x1;2 =
| 3 ± √ 3 2 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 2 | x2 = 1 |
Запишем координаты точек пересечения графика с осью « Ox »: и .
Теперь найдем координаты точки пересечения с осью « Oy ».
Как видно на рисунке выше, координата « x » точки пересечения с осью « Oy » равна нулю.
Подставим « x = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем координату точки по оси « Oy ».
y(0) = 0 2 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Ответ: точки пересечения с осью « Ox »: (·) A (2; 0) и (·) B (1; 0) .
С осью « Oy »: (·)C (0; 2) .
Как определить при каких значениях x функция принимает положительные или отрицательные значения
Напоминаем, что когда в задании говорится « функция принимает значения» — речь идет о значениях « y » . Другими словами, необходимо ответить на вопрос: при каких значениях « x », координата « y » положительна или отрицательна.
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
- провести прямые через точки в местах, где график пересекает ось « Ox »;
- определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
- записать ответ для каждого промежутка относительно « x ».
С помощью графика квадратичной функции, изображенного на рисунке, ответить: При каких значениях « x » функция принимает 1) положительные значения; значения.
Проведем через точки, где график функции пересекает ось « Ox » прямые.
Определим области, где функция принимает отрицательные или положительные значения.
Подпишем над каждой полученной областью, какие значения принимает « x » в каждой из выделенных областей.
Ответ: при « x » и « x > 2 » функция принимает отрицательные значения; при функция принимает положительные значения.
Источник
Взаимное расположение графиков квадратных трёхчленов
Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
- ось симметрии $x = -frac<2a>$
- вершину параболы на оси симметрии $(–frac<2a>; -frac<4a>)$
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c) .
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$ , парабола имеет две точки пересечения с $x_1,2 = frac<-b pm sqrt><2a>$ на оси OX.
Если D = 0 , парабола имеет одну точку пересечения $x_0 = -frac<2a>$, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Точки пересечения параболы с осью OX






Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.
Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
$ a_1 = a_2, b_1 = b_2, $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$
$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
Параболы имеют вид
У них общая ось симметрии
$ x = -frac<2a>$, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет
$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Одна точка пересечения
$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Абсцисса точки пересечения
Одна точка пересечения (касание)
$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)
$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Не пересекаются, если
Две точки пересечения
Пересекаются в двух точках
Две точки пересечения
$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
Две точки пересечения,
одна из которых (0;c)
$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
Все параметры парабол разные
Две точки пересечения
Две точки пересечения
Одна точка пересечения (касание)
Одна точка пересечения
Точек пересечения нет
Точек пересечения нет
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
Пересечение с осью OY: $<left< begin x = 0 \ y = -1end right.>$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
$ Rightarrow left[ begin <left< begin x = frac<1> <3>\ y = 0 end right.> \ <left< begin x = -1 \ y = 0 end right.> end right.$ — две точки пересечения
Пересечение с осью OY: $<left< begin x = 0 \ y = 1end right.>$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
$ Rightarrow left[ begin <left< begin x = frac<1> <4>\ y = 0 end right.> \ <left< begin x = -1 \ y = 0 end right.> end right.$ — две точки пересечения
Пересечение с осью OY: $<left< begin x = 0 \ y = 1end right.>$
Пересечение с осью OX:
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
Пересечение с осью OY: $<left< begin x = 0 \ y = -4end right.>$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow <left< begin x = 2 \ y = 0 end right.>$$ — одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$
Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac<2>-3x+1$.
$$ x_0 = — frac <2a>= — frac<-3><2 cdot frac<1><2>> = 3, D = b^2-4ac = 3^2-4 cdot frac<1> <2>cdot 1 = 7 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ <left< begin a = 1 \ b = -6a = -6 \ D = 14a = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ b^2-4ac = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ 36-4c = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ c = frac<36-14> <4>= 5,5 end right.>$$
$$ <left< begin a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end right.> Rightarrow <left< begin a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end right.> Rightarrow <left< begin a = -0,2 \ b = 1,2 \ c = — frac<1,44+2,8> <0,8>= -5,3 end right.> $$
$$ y = frac<2>-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)
Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac<3>-2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac <2a>= -frac<-2><2 cdot frac<1><3>> = 3, D = b^2-4ac = 2^2-4 cdot frac<1> <3>cdot 5 = — frac<8> <3>$$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
Источник
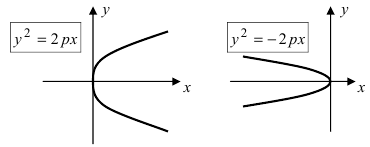
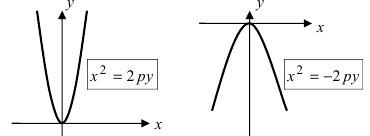
Парабола:
Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.
Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы
Рис. 34. Парабола, (уравнение директрисы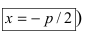
Возведем обе части уравнения в квадрат
Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: 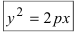
Рис. 35а. Параболы и их уравнения.
Рис. 356. Параболы и их уравнения.
Найдем координаты точек пересечения параболы с координатными осями:
Определение: Точка О(0; 0) называется вершиной параболы.
Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка 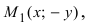
Пример:
Дано уравнение параболы 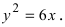
Решение:
Так как из уравнения параболы 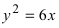
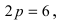
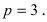
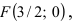
Пример:
Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы 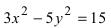
Решение:
Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.
Гипербола:
Следовательно, действительная полуось гиперболы 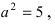
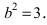
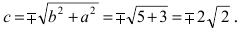
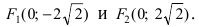
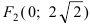
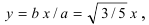
Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:
Пример:
Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса 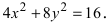
Решение:
Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:
Следовательно, большая полуось эллипса 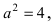
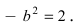
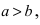
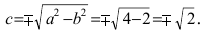
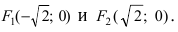
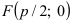
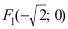
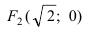

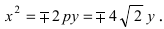
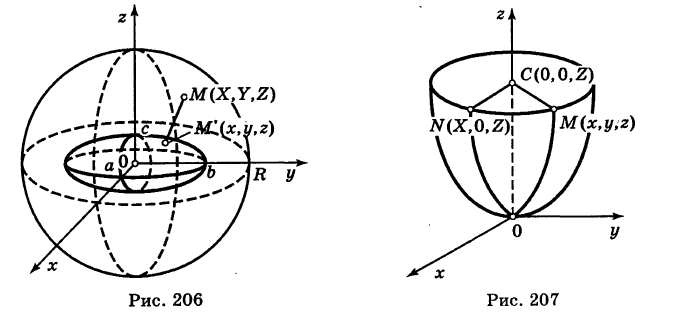
Уравнение параболоида вращения
Пусть вертикальная парабола
расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).
Для вывода уравнения поверхности рассмотрим произвольную точку 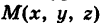
Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем
Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения
Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Многогранники
- Окружность
- Эллипс
- Гипербола