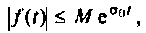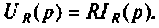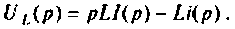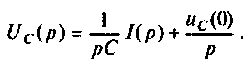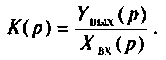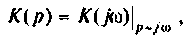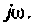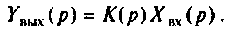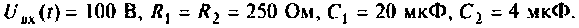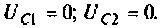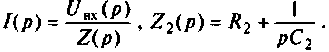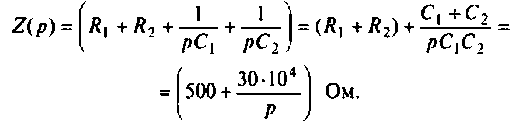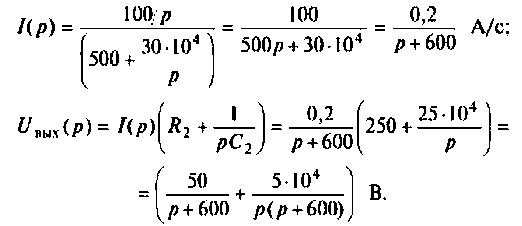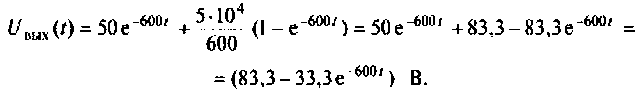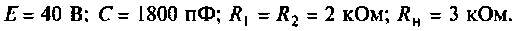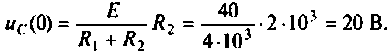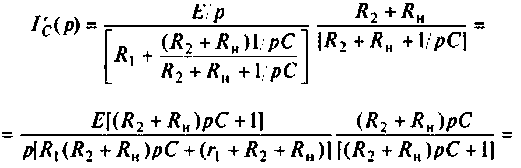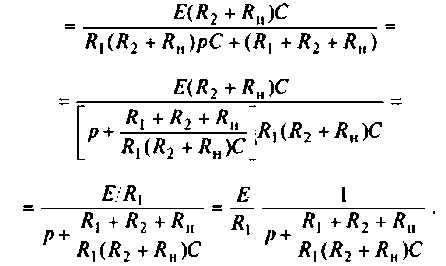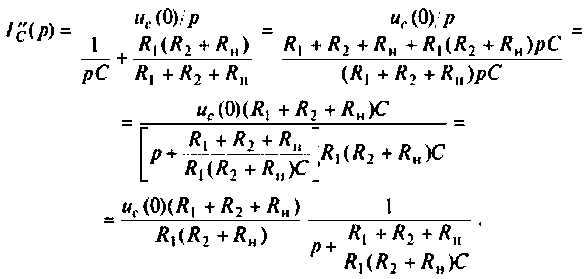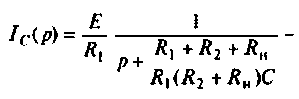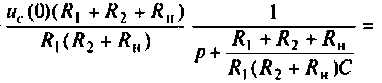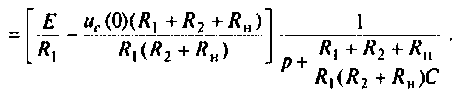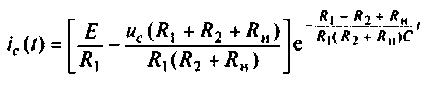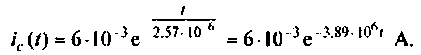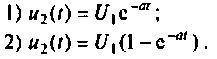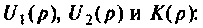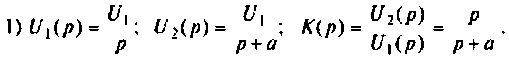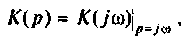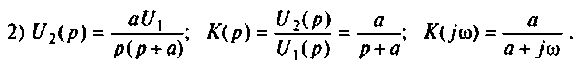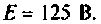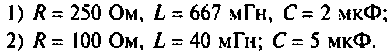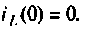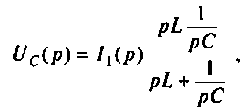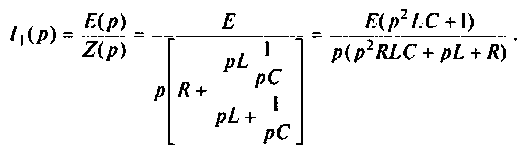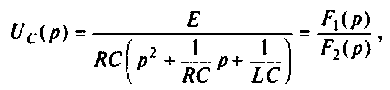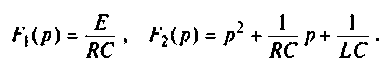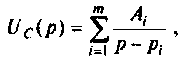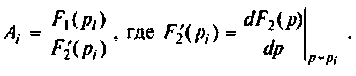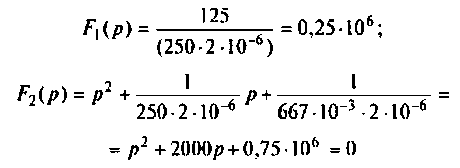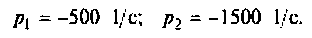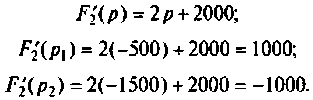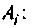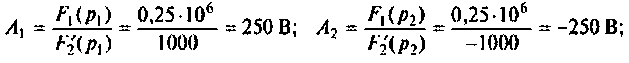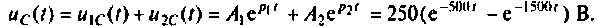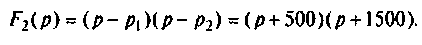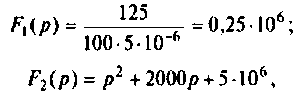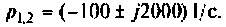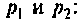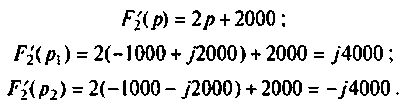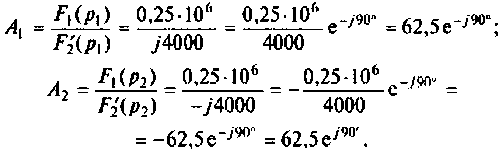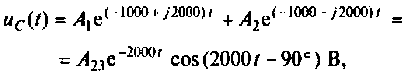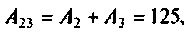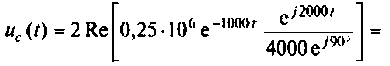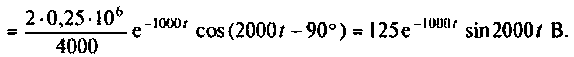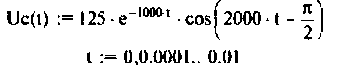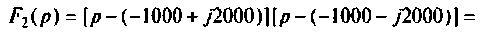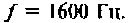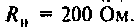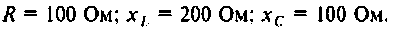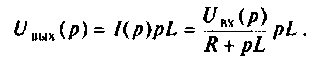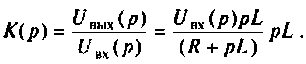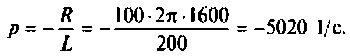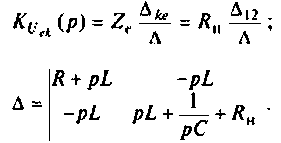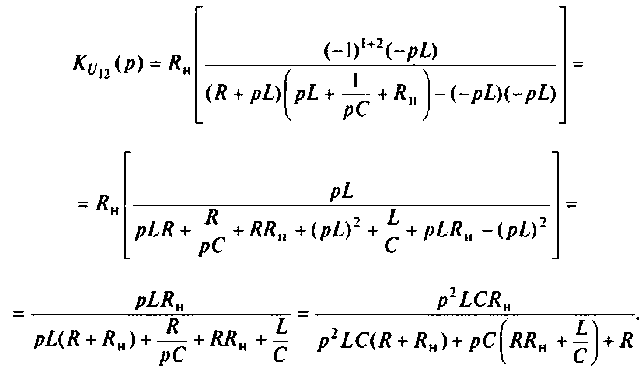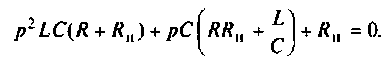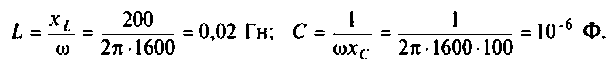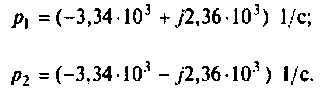Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Свойства передаточных функций
Определение 1
Передаточная функция – это способ математического описания динамической системы.
Передаточная функция в основном используется в цифровой обработке сигналов, а также в теории управления. Она представляет собой дифференциальный оператор, который выражает связь между выходом и входом линейной стационарной системы. Если известны передаточная функция и входной сигнал системы, то можно восстановить выходной сигнал. В теории управления передаточная функция непрерывной системы является отношением преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.
Определение 2
Преобразование Лапласа – это интегральное преобразование, которое связывает между собой функцию комплексного переменного с функцией вещественного переменного.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Передаточная функция какой-либо системы определяет все ее динамические свойства, таким образом первоочередная задача расчета системы управления сводится к определению ее передаточной функции. К основным свойствам передаточных функций относятся:
- Импульсная переходная функция представляет собой оригинал для передаточной функции.
- В физически реализуемых системах порядок полинома числителя передаточной функции не может быть больше порядка полинома ее знаменателя.
- Числитель и знаменатель передаточной функции представляют собой характеристические полиномы дифференциального уравнения перемещения линейной системы. Полюса передаточной функции являются корнями характеристического полинома знаменателя, а нули корни характеристического полинома числителя.
- Для систем с неизменяемыми параметрами компонентов и с сосредоточенными параметрами передаточная функция представляет собой дробно-рациональную функцию
Передаточная функция электрической цепи. Пример решения задач
Передаточная функция линейной электрической цепи представляет собой отношение электрической выходной величины к входному воздействию, которые выражены в операторной форме и рассматриваются при нулевых начальных условиях, таким образом выражение передаточной функции выглядит следующим образом:
«Передаточная функция» 👇
$Н(р) = F2(p) / F1(p)$
где: F2 — выходная электрическая величина; F1 — входное воздействие.
Различают следующие основные виды передаточных функций для электрических цепей:
- Безразмерная (по напряжению) передаточная функция.
- Фазо-частотная характеристика.
- Амплитудно-частотная характеристика.
Общий вид передаточной функции по напряжению, которая очень часто используется для анализа электрических цепей частотными методами, следующий:
$H(jw) = F2(jw)/F1(jw)$
Рассмотрим схему электрической цепи, которая представлена на рисунке ниже:
Рисунок 1. Схема цепи. Автор24 — интернет-биржа студенческих работ
В комплексном виде передаточная функция для нее будет выглядеть следующим образом:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
В вышеприведенном выражении модуль:
$|Hu(jw)|=Hu(w)=U2(w) / U1(w)$
Рассмотрим схему, которая представлена на рисунке ниже
Рисунок 3. Схема. Автор24 — интернет-биржа студенческих работ
Необходимо определить коэффициент передачи по напряжению, а также амплитудно-частотную и фазо-частотную характеристики для вышеприведенной цепи. Для нее формула для расчета коэффициента передачи по напряжению будет иметь следующий вид:
$Hu(jw) = U2(jw) / U1(jw)$
Выражение комплексной функции U2(jw) будет иметь следующий вид:
$U2 = I(jw)*(1/jwC)=U1(jw) / (R+(1/jwC)) * 1/jwC = U1(jw) / (1+(jwRC)$
Если мы подставим формулу для U2 в выражение для Hu(jw), то получим комплексную передаточную функцию следующего вида:
$Hu(jw) = 1/(1+jwR*C)$
Таким образом амплитудно-частотную характеристику рассматриваемой цепи можно выразить:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Фазо-частотная характеристика определяется по формуле:
$фu = -arctgwR*C$
Если изменять частоту (w) от 0 до определенного значения, можно изобразить графики фазо-частотной и амплитудно-частотной характеристик.
Рисунок 5. Графики. Автор24 — интернет-биржа студенческих работ
Амплитудно-частотная и фазо-частотная характеристики могут быть представлены единым графиком, если построить зависимость комплексной передаточной функции от частоты w на комплексной плоскости. В данном случае конец вектора передаточной функции будет описывать кривую, называемую годографом комплексной передаточной функции.
Рисунок 6. График. Автор24 — интернет-биржа студенческих работ
В некоторых случаях оперируют таким понятием, как логарифмическая амплитудно-частотная характеристика
$К =20lgН(w)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Важнейшей
характеристикой линейной электрической
цепи является комплексная
передаточная функция H(jω).
При этом электрическую цепь удобно
изображать в виде четырехполюсника
(рис. 4.1), на входные зажимы (1 — 1’) которого
подается сигнал в виде напряжения с
комплексной амплитудой Uт1, или
тока с комплексной амплитудой Im1,
а реакция снимается с выходных зажимов
(2 — 2′) также в виде напряжения или тока
с комплексными амплитудами Um2, Im2. Комплексная
передаточная функция (КПФ) определяется
как отношение комплексной амплитуды
реакции цепи к комплексной амплитуде
входного воздействия.
В
зависимости от типов входного воздействия
и реакции цепи различают следующие виды
КПФ:
1. Комплексная
передаточная функция по напряжению
Комплексные
передаточные функции определяются на
частоте со сигнала воздействия и зависят
только от параметров цепи.
Как
всякую комплексную величину H(jω) можно
представить в показательной,
тригонометрической и алгебраической
форме:
есть
вещественная и мнимая
части комплексной
передаточной функции цепи.
Из
(4.5) —(4.8) нетрудно получить соотношения,
связывающие АЧХ и ФЧХ с вещественными
и мнимыми частями комплексной передаточной
функции
АЧХ
и ФЧХ являются наиболее фундаментальными
понятиями теории цепей и широко
используются на практике. Важность этих
характеристик для систем электрической
связи, радиовещания и телевидения
объясняется самой природой передачи
сигналов определенного спектрального
состава по каналам связи. Требования
к АЧХ и ФЧХ различных устройств являются
определяющими при проектировании
любой аппаратуры связи, так как от
степени их выполнения во многом зависит
качество передачи информации.
Пример. Определить
КПФ по напряжению Hu(jω),
АЧХ и ФЧХ цепи, изображенной на рис. 4.2.
Согласно (4.1) запишем:
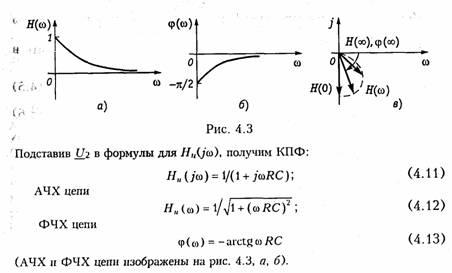
АЧХ
и ФЧХ цепи можно представить единым
графиком, если построить зависимость
КПФ H(jω)
от частоты со на комплексной плоскости.
При этом конец вектора H(jω)
опишет некоторую кривую, которая
называется годографом комплексной
передаточной функции (рис. 4.3, в).
В
ряде случаев частотные характеристики
цепи могут изменяться в очень широких
пределах, поэтому более удобно их
оценивать в логарифмическом масштабе.
С этой целью для оценки АЧХ вводят
понятие логарифмической
амплитудно-частотной характеристики (ЛАХ):
Оценивается
ЛАХ согласно (4.14) в децибелах (дБ). В
активных цепях К называют
еще логарифмическим
усилением. Для
пассивных цепей вместо коэффициента
усиления оперируютослаблением
цепи:
которое
также оценивается в децибелах.
Наряду
с передаточными функциями (4.1) —(4.4) в
ряде случаев (см. гл. 16, 17,18) находят
применение комплексные функции,
определяющиеся отношением комплексной
реакции к комплексному воздействию
на входных зажимах электрической цепи
(рис. 4.4)
Функции
вида (4.16) носят название комплексных
входных функций цепей.
3.2. Частотные характеристики последовательного колебательного контура
В
радиотехнике и электросвязи большое
значение имеет явление
резонанса. Резонансом называют
такое состояние электрической цепи,
состоящей из разнохарактерных реактивных
элементов, при котором фазовый сдвиг
между входным током и приложенным
напряжением равен нулю. Цепи, в которых
возникает явление резонанса,
называют колебательными
контурами,или резонансными
цепями.
Колебательные
контуры и явления резонанса находят
широкое применение в радиотехнике и
электросвязи. Резонансные цепи являются
составной частью многих радиотехнических
устройств: избирательные цепи в
радиоприемниках и усилителях,
частотно-зависимые элементы
автогенераторов, фильтров, корректоров,
других устройств. Для получения
высоких технико-экономических показателей
(избирательности, полосы пропускания,
коэффициента прямоугольности,
равномерности и т. д.) резонансные цепи
должны иметь достаточно сложную структуру
(многоконтурные связанные цепи, активные
резонансные системы и др.). Некоторые
из этих систем будут рассмотрены в гл.
15, 17. В настоящей главе изучим основные
особенности работы цепей в режиме
резонанса на примере простейших
колебательных контуров.
Простейший
колебательный контур содержит индуктивный
и емкостный элементы, соединенные
последовательно {последовательный
контур) или
параллельно (.параллельный
контур).В
последнее время широкое распространение
получили резонансные цепи на базе
операционных усилителей (ОУ). Различают
два типа резонансов: напряжений и
токов. В последовательном контуре
возникает резонанс
напряжений, а
в параллельном — резонанс
токов.
Частоту,
на которой наблюдается явление резонанса,
называют резонансной.
На
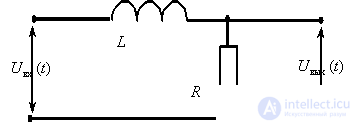
рис. 4.5 изображена схема последовательного
контура с реактивными элементами L и С и
резистивным сопротивлением R, характеризующим
потери в контуре. Приложим к контуру
гармоническое напряжение с
частотой ω. Комплексное входное
сопротивление контура на данной частоте
определяется согласно уравнению
На
резонансной частоте комплексное
сопротивление носит чисто активный
характер, т. е. Z = R, ток
совпадает по фазе с приложенным
напряжением и достигает максимального
значенияIо
= U/R. Реактивные
сопротивления контура на резонансной
частоте ω0 равны
друг другу:
Величина
ρ носит название характеристического
сопротивления контура.
Резонансные
свойства контура характеризуются добротностью
контура, которая
в общем случае определяется величиной
где Wp —
максимальные значения реактивной
энергии, запасенной в контуре при
резонансе; WT — активная
энергия, поглощаемая в контуре за
период Т. Величина,
обратная добротности, называется затуханием
контура и
обозначается d:
Величина Q безразмерна
и обычно колеблется для реальных контуров
от 10 до 100 и выше. Для выяснения физического
смысла параметра Q исследуем
энергетические соотношения в контуре
при резонансе. Положим, например, что
при резонансе ток в цепи Определим
согласно (1.10) и (1.13) сумму энергий
электрического и магнитного полей:
так
как уменьшение WL сопровождается
увеличением We и
наоборот. Таким образом,
происходит
периодический обмен энергией между
элементами I и
С без участия источника. Энергия
источника расходуется только на
покрытие тепловых потерь в элементе
активного сопротивления R; реактивная
мощность при резонансе не потребляется.
Активная
энергия, рассеиваемая в контуре за
период Т, равна
Таким
образом, добротность Q показывает,
во сколько раз резонансные напряжения
на реактивных элементах превышают
приложенное напряжение. Отсюда
следует и термин «резонанс напряжений».
Это свойство контура «усиливать»
приложенное напряжение резонансной
частоты широко используется на практике.
Величины
ρ, ωо, Q, d являются вторичными
параметрами контура
в отличие от величин R, L,
С называемых первичными.
Анализируя
характер уравнений напряжений и
токов в RLC-цепи,
фазовых сдвигов между ними при
гармоническом воздействии нетрудно
видеть, что они являются
частотно-зависимыми. Эта зависимость
вытекает непосредственно из зависимости
реактивных
элементов XL И ХС .ОТ
Из
представленных характеристик следует,
что при ω <ω0 цепь
имеет емкостный характер (Х<0; φ <0)И
ТОК опережает
по фазе приложенное напряжение при ω
>ω0 характер
цепи индуктивный (X >
0; φ > 0) и ток отстает по фазе от
приложенного напряжения; при со = соо
наступает резонанс напряжений (X = 0;
φ = 0) и ток совпадает по фазе с приложенным
напряжением. Полное сопротивление
цепи принимает при этом минимальное
значение Z = R.
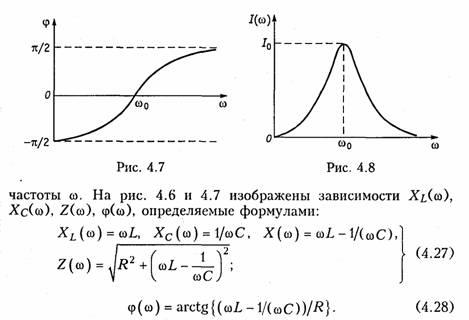
Зависимость
действующего значения тока от частоты
можно найти из уравнения (4.18)*:
Зависимости I(ω), UL(ω), UC(ω) называются резонансными
характеристиками тока и напряжений. Анализ
зависимости I(ω)
показывает, что она достигает максимума
при резонансе ω =ω0
Выходное
напряжение обычно снимается с емкостного
или индуктивного элемента контура.
В соответствии с этим представляет
наибольший практический интерес КПФ
по напряжению относительно элементов
С и L:
Анализ
полученных зависимостей показывает,
что с увеличением добротности Q (уменьшением
затухания d) частоты
ωс и ωL сближаются
с резонансной частотой ωо.При
этом CCт и HLmвозрастают.
Степень
отклонения режима колебательного
контура от резонанса принято
оценивать абсолютной,
относительной и обобщенной
расстройками. Отклонение
от резонансного режима может происходить
в результате изменения частоты; задающего
генератора или
вариации параметров
контура.
Расстройки
определяются следующим образом:
абсолютная
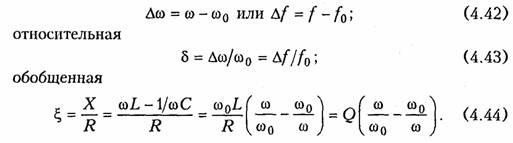
Наиболее
широко в теоретических исследованиях
применяется обобщенная расстройка ζ, так
как ее использование существенно
упрощает расчет. Например, модуль входной
проводимости можно записать через
обобщенную расстройку ζ, в форме
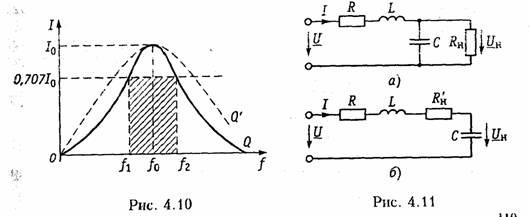
Важной
характеристикой колебательного контура
является полоса пропускания. В общем
случае абсолютной
полосой пропускания называют
диапазон частот в пределах которого
коэффициент передачи уменьшается в √2
раз по сравнению с максимальным*.
Абсолютная полоса пропускания равна
Уравнения
(4.50) могут быть положены в основу
экспериментального определения
добротности по резонансной кривой
тока I(ω).
Формула (4.50) показывает, что чем выше
добротность Q,
тем меньше полоса пропускания и наоборот.
Причем, поскольку с увеличением
потерь R добротность
контура падает, то подключение к
контуру сопротивления нагрузки или
источника с внутренним сопротивлением
приводит к расширению полосы пропускания.
Пример. Определить
полосу пропускания контура, нагруженного
на резистивное
сопротивление Rн (рис.
4.11, й).
Преобразуем
параллельный участок С и RH в
эквивалентный последовательный с
помощью формул (3.56):
т.
е. при подключении высокоомной нагрузки
к контуру его резонансная частота
не изменяется, но увеличиваются потери
в контуре (рис. 4.11, б). При этом уменьшается
добротность Q’
= p/(R+RH’)
и увеличивается полоса пропускания
контура (4.10).
В
заключение следует отметить, что на
практике обычно используются
высокодобротные контуры, причем
низкоомные нагрузки подключаются к
контурам через различные согласующие
устройства (трансформаторы, повторители
и др.). Для получения высоких качественных
характеристик (большого входного и
низкого выходного сопротивлений, высокой
добротности, малой чувствительности
резонансной частоты и выходного сигнала
от нагрузки) применяют электронные
аналоги колебательных контуров,
реализуемых на базе зависимых
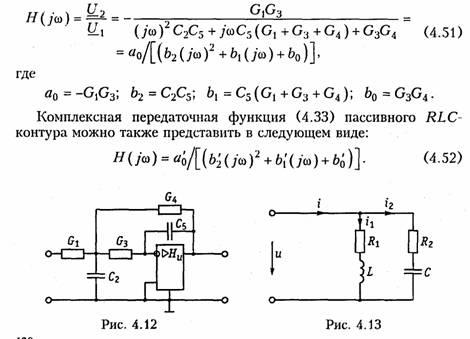
источников. На рис. 4.12 изображена схема
колебательного контура, реализованного
на базе ARC-звена,
второго порядка (рис. 3.37, а), где
принято Y1 = G1; Y2 =jωC2; Y3 = Gз; Y4 = G4; Y5 = jωC5.
При этом комплексная передаточная
функция цепи с учетом (3.138)
где т.
е. (4.52) совпадает с (4.51) с точностью до
постоянных множителей.
Таким
образом, с помощью рассмотренной активной
цепи можно получить электронный
аналог колебательного контура. На базе
активных элементов можно реализовать
и другие схемы электронных аналогов
колебательных контуров, важным
преимуществом которых является отсутствие
индуктивностей, высокое значение
добротности, слабо зависящей от нагрузки,
легкость перестройки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
7.1. Преобразование Лапласа и его свойства
7.2. Теорема разложения
7.3. Расчет переходных процессов операторным методом
7.4. Операторные передаточные функции
7.5. Вопросы и задания для самопроверки
7.1. Преобразование Лапласа и его свойства
Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраическими уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.
В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:
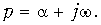
При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.
Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением.
где f(t) — функция действительного переменного t, определенная при t 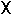
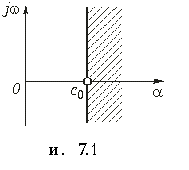
где множитель М и показатель роста с0 — положительные действительные числа. На рис. 7.1 изображена область определения функции комплексного переменного F(p).
Обратное преобразование Лапласа определяют из решения (7.2):
Функция F(p), определяемая уравнением (7.2), носит название изображения по Лапласу, а функция f(t) в (7.4) — оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного (t) и комплексного (p) переменного, связанных преобразованием Лапласа. Для сокращенной записи преобразований (7.2), (7.4) используют следующую символику
где L — оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия 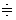
Рассмотрим основные свойства преобразований Лапласа.
Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме
где ak — постоянные коэффициенты разложения. Свойство (7.5) легко доказать, если применить к левой части соотношения (7.5) прямое преобразование Лапласа (7.2).
Дифференцирование оригинала
При ненулевых начальных условиях: f(0–)¹ 0 дифференцирование оригинала соответствует следующему условию
Для доказательства (7.6) подставим f¢(t) в преобразование (7.2) в виде
Отсюда после интегрирования по частям получаем:
В случае нулевых начальных условий
Интегрирование оригинала
Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).
Изменение масштаба независимого переменного (теорема подобия)
где а — постоянный вещественный коэффициент. Свойство (7.9) легко доказывается путем замены независимой переменной t = atв прямом преобразовании Лапласа (7.2).
Смещение в области действительного переменного (теорема запаздывания)
Для доказательства (7.10) введем следующие обозначения:
Осуществим замену переменной t = t ± t0.
что и требовалось доказать.
Из соотношения (7.10) следует, что сдвиг оригинала по оси времени на t0 соответствует умножению изображения на 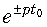
Смещения в области комплексного переменного (теорема смещения)
Теорема (7.11) следует непосредственно из прямого преобразования Лапласа, если в (7.2) вместо f(t) подставить 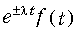
Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности)
Для доказательства свойств (7.12), (7.13) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (7.2) по параметру х.
Произведение изображений
Интегралы в (7.14) носят название свертки функций f1(t) и f2(t).
Дифференцирование изображения
Свойство (7.15) легко доказывается путем дифференцирования прямого преобразования Лапласа (7.2).
Интегрирование изображения
Данное свойство доказывается аналогично (7.15).
В заключение приведем предельные соотношения для оригинала и изображения:
Действительно, согласно свойства дифференцирования оригинала можно записать:
Учитывая, что 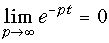
Отсюда непосредственно следует соотношение (7.17). Аналогично доказывается равенство (7.18).
В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции d(t) (функция Дирака).
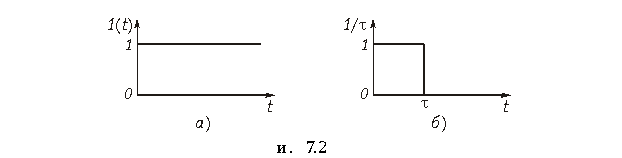
Единичная функция
Единичная функция задается уравнением (рис. 7.2, а)
Изображение функции (7.19) будет равно:
Единичная импульсная функция (функция Дирака)
Эта функция называется еще d-функцией; она задается уравнением
Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при t ® 0) единичного импульса (см. рис. 7.2, б), площадь которого равна единице:
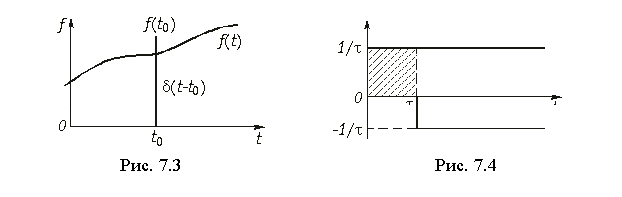
Одним из интересных свойств функции d(t) является ее фильтрующее свойство, определяемое равенством (рис. 7.3):
Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на t (рис. 7.4). Для этих функций с учетом теоремы запаздывания имеем:
Для результирующего изображения с учетом свойства линейности получим
Устремив t ® 0, найдем изображение единичной импульсной функции (d-функции):
Экспоненциальный сигнал 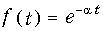
т. е.
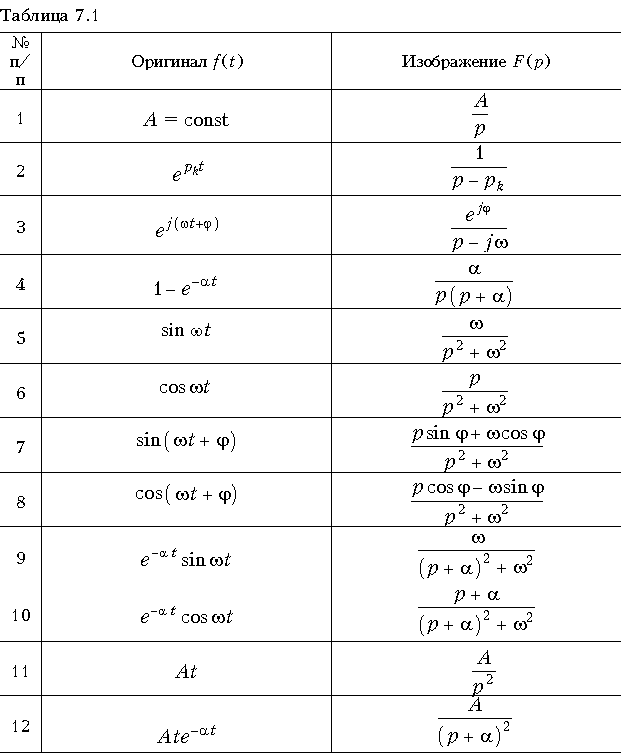
Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.
7.2. Теорема разложения
Для нахождения оригинала по изображению можно воспользоваться либо таблицами, либо использовать обратное преобразование Лапласа (7.4). Однако вычисление оригинала с помощью (7.4) обычно оказывается весьма сложным. Поэтому, для упрощения расчетов применяют теорему разложения, которая позволяет при нахождении оригинала заменить операцию интегрирования в (7.4) операцией суммирования, что значительно упрощает вычисления. Наиболее строгий вывод этой теоремы можно осуществить на основании теоремы вычетов. Здесь мы ограничимся выводом формул разложения применительно к изображению, представляющему собой рациональную дробь:
где 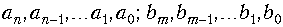
Для нахождения оригинала f(t) разложим F(p) на простые дроби:
где pk — простые корни характеристического уравнения
Ak — коэффициенты разложения.
Для того, чтобы найти коэффициент Ak домножим обе части (7.26) на (р — pk) и перейдем к пределу:
Раскрывая неопределенность в левой части равенства (7.28) по правилу Лопиталя и учитывая, что согласно (7.27) правая часть (7.28) равна Ak, получаем
Подставив значения Ak в формулу (7.26), найдем:
Если учесть, что изображение 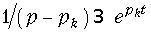
Формула (7.30) является математической формулировкой теоремы разложения и позволяет найти оригинал по изображению в виде (7.25), в случае простых корней. Если среди корней pk имеется один нулевой корень, т. е. F2(р) = pF3(p), то теорема разложения примет вид
Формулу (7.31) можно получить, если подставить в (7.30) вместо F2(р) значение pF3(р) и осуществить операцию дифференцирования.
Если среди корней уравнения (7.27) (полюсов функции F(p)) имеются комплексно-сопряженные корни pk и pk+1, то в формуле (7.30) достаточно взять pk, а для pk+1 взять сопряженное значение, при этом сумма соответствующая двум этим корням с учетом действительности f(t) будет равна
При этом в уравнении для f(t) появятся составляющие типа (6.9): 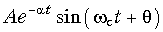
Теорему разложения можно обобщить и на более общие случаи. В частности, если среди полюсов (7.25) имеются полюса кратности l, то в оригинале f(t) появятся слагаемые типа (6.8).
Пример. Задано изображение в виде
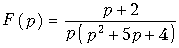
Обозначим F1(p) = p + 2; F2(p) = p(p2 + 5p + 4). При этом получим F(p) в виде (7.25). Найдем корни характеристического уравнения F2(p) = p(p2 + + 5p + 4) = 0.
При этом F1(p1) = 2; F1(p2) = 1; F1(p3) = –2.
Определим производную
Отсюда F2¢(p1) = 4; F2¢(p2) = –3; F2¢(p3) = 12. Воспользовавшись формулой (7.30), окончательно получим:
Учитывая, что среди корней характеристического уравнения F2(p) = 0 имеем один нулевой корень, при нахождении f(t) можно было воспользоваться и формулой (7.31). Действительно, если обозначим
то получим
Тогда корни уравнения F3(p) = 0 будут равны p1 = —l, p2 =—4. С учетом значений
согласно (7.31) окончательно получим
что полностью совпадает с ранее полученным решением.
7.3. Расчет переходных процессов операторным методом
Пользуясь основными свойствами преобразования Лапласа, можно получить основные законы теории цепей в операторной форме. Рассмотрим, например, последовательный RLC-контур (см. рис. 6.14), находящийся при ненулевых начальных условиях uC(0–) ¹ 0; iL(0–) ¹ 0. Для этого контура уравнение по ЗНК имеет вид:
Применив к (7.33) прямое преобразование Лапласа и принимая во внимание свойства линейности, дифференцирования и интегрирования оригинала получим:
Отсюда получаем закон Ома в операторной форме для данной цепи:
где U0(p) = U(p) + Li(0) — uC(0)/p носит название операторного напряжения; Z(p) = R + pL + 1/pC — операторного сопротивления цепи. Если в Z(p) заменить р на jw, то получим комплексное сопротивление цепи. Величины Li(0) и uC(0)/p называют расчетными напряжениями. Они характеризуют энергию магнитного и электрического полей, запасенную в L и С к моменту коммутации. Величина, обратная Z(p) называется операторной проводимостью цепи:
Для нулевых начальных условий закон Ома примет вид
Аналогичным образом можно получить законы Кирхгофа в операторной форме:
первый закон (ЗТК)
второй закон (ЗНК)
Таким образом, закон Ома и законы Кирхгофа в операторной форме аналогичным этим же законам в комплексной форме (см. (3.48)—(3.50)) с той лишь разницей, что в (7.37) в каждой из п ветвей при наличии ненулевых начальных условий действуют дополнительные расчетные источники Lkik(0) и —uCk(0)/р, положительное направление которых совпадает с выбранным положительным направлением тока в этой ветви.
Используя законы Ома и Кирхгофа в операторной форме, можно найти изображения искомых токов и напряжений в цепи. Для определения оригиналов токов и напряжений можно воспользоваться либо таблицами оригиналов и изображений, либо применить теорему разложения.
Для иллюстрации основных теоретических положений найдем операторным методом закон изменения тока в последовательном RLC-контуре при включении его на источник постоянного напряжения. Уравнение для изображения тока можно найти по закону Ома для нулевых начальных условий (7.35) с учетом изображения постоянного напряжения U(p) U/p:
Найдем корни характеристического уравнения
При R > 2r корни будут вещественны и различны. Для нахождения оригинала тока i(t) воспользуемся теоремой разложения (7.30). Для этого найдем производные F2¢(p1) и F2¢(p2):
Подставив значения F1(p) = F1(p2) = CU и F2¢(p1) и F2¢(p2) в (7.30) получим оригинал тока
что полностью совпадает с ранее полученным уравнением (6.68).
Из рассмотренного примера хорошо видны преимущества операторного метода: простота, отсутствие громоздких операций по определению постоянных интегрирования. Следует подчеркнуть, что базируясь на законах Ома и Кирхгофа в операторной форме, можно рассчитать переходный процесс любым из ранее рассмотренных методов: контурных токов, узловых напряжений и др. При этом удобно пользоваться эквивалентными операторными схемами. При составлении эквивалентных операторных схем источники тока и напряжений i(t) и u(t) заменяются соответствующими изображениями I(p) и U(p), индуктивность L заменяется на pL, а емкость С — на 1/pC при нулевых начальных условиях. Если начальные условия ненулевые, то последовательно с pL добавляется источник напряжения Li(0), а с С — источник напряжения — uC(0)/р (рис. 7.5)
* Возможны схемы замещения заряженной емкости uC(0) и индуктивности с током iL(0) с помощью источников тока с задающими токами CuC(0) и iL(0)/p соответственно.
Например, эквивалентная операторная схема для цепи, изображенной на рис. 6.17, будет иметь вид (рис. 7.6). Составив для этой схемы уравнения по законам Кирхгофа в операторной форме, получим систему алгебраических уравнений, решение которых существенно проще системы (6.86).
Операторный метод можно использовать и для решения уравнения состояния цепи. При этом уравнение состояния (6.94) с учетом свойств дифференцирования оригинала и линейности преобразования Лапласа примет вид:
где Х(р), W(p) — изображения векторов состояния x(t) и входных воздействий W(t).
Из (7,38) получаем непосредственно решение
где I — единичная матрица. Применив к (7.39) теорему разложения, можно получить искомый вектор состояния
7.4. Операторные передаточные функции
Важную роль в методах анализа и синтеза электрических цепей при нулевых начальных условиях играют операторные передаточные функции, которые определяются как отношение изображения выходной реакции цепи к изображению входного воздействия. В соответствии с этим определением различают четыре вида передаточных функций:
где Ни(р), Hi(p) имеют смысл операторных передаточных функций по напряжению и току; НL(р); НY(р) —операторные передаточные сопротивление и проводимость соответственно.
Если в (7.40) заменить оператор р на jw, то получим уравнение комплексных передаточных функций Н(jw), широко используются при частотных методах анализа электрических цепей.
Зная передаточную функцию цепи Н(р), с помощью (7.40) нетрудно найти изображение реакции цепи, а следовательно, и саму реакцию на заданное воздействие.
Операторную передаточную функцию Н(р) для пассивной цепи можно представить как дробно-рациональную функцию с вещественными коэффициентами:
или в виде
где p01, p02, …, p0n — нули; p1, p2, …, pm — полюсы передаточной функции; Н = аn/bm.
Степени полиномов числителя п и знаменателя т зависят от числа реактивных элементов пассивной цепи.
Заменив в (7.41) оператор р на jw, получим комплексную передаточную функцию цепи
где АЧХ цепи
ФЧХ цепи
Учитывая, что согласно (7.43) |H(jw)| является иррациональной, обычно при анализе и синтезе цепей имеют дело с квадратом АЧХ:
где коэффициенты сk и dk получаются путем объединения коэффициентов при одинаковых степенях переменной w.
Перечислим основные свойства операторных передаточных функций и квадрата АЧХ пассивных цепей:
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Полюсы передаточной функции располагаются в левой полуплоскости комплексной переменной р. На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции Ни(р) = U2(р)/U1(р). Выберем входное воздействие u1(t) = d(t) или в операторной форме U(р) = l. Изображение выходного напряжения U2(р) = U1(р)Ни(р) в этом случае численно равно Ни(р), т. е.
где w(p) — полином числителя передаточной функции; A1, A2, …, Am, —коэффициенты разложения дробно-рациональной функции на сумму простых дробей.
Перейдем от изображения U2(p) к оригиналу u2(t):
где в общем случае pi = ai + jwi.
В пассивных и устойчивых активных четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что в (7.46) вещественные части полюсов pi должны быть отрицательными (ai < 0), т. е. полюсы должны находиться в левой полуплоскости переменной р.
3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей, т. е. п < т. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.
4. Квадрат АЧХ является четной рациональной функцией переменной w с вещественными коэффициентами. Это свойство с очевидностью вытекает из способа получения квадрата АЧХ по передаточной функции.
5. Квадрат АЧХ не может принимать отрицательных и бесконечно больших значений при w > 0. Неотрицательность 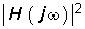
7.5. Вопросы и задания для самопроверки
1. В чем заключается сущность операторного метода расчета цепи?
2. Что такое операторное сопротивление цепи?
3. Что такое операторные схемы замещения при составлении эквивалентной операторной схемы?
4. 
Чем заменяются индуктивности и емкости в операторной схеме замещения?
5. Как учитываются независимые начальные условия?
6. Записать закон Ома и законы Кирхгофа в операторной форме.
7. Что такое единичная функция и d-функция?
8. Что понимается под операторной передаточной функцией? Каковы ее свойства?
9. Каким образом можно перейти от изображения к оригиналу?
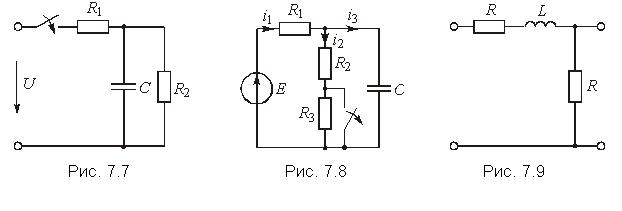
10. Для схемы, изображенной на рис. 7.7, операторным методом определить напряжение на конденсаторе uC(t). U = 20 В; R1 = = R2 = 100 Ом; С = 4 мкФ.
Ответ: uC(t) = 10 – 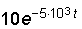
11. Для схемы, изображенной на рис. 7.8, найти изображение тока I2(p).
Ответ: I2(p) = 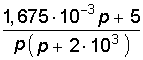
12. Зная изображение тока (рис. 7.8), определить оригинал i2(t).
Ответ: i2(t) = 2,5 – 0,825 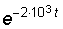
13. Для схемы, изображенной на рис. 7.9, определить: 1) операторную передаточную функцию Hu(p); 2) найти АЧХ цепи. Ответ: 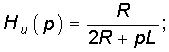
Привет, Вы узнаете про понятие линейного динамического звена передаточная функция структурная схема временные характеристики динамического звена , Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
понятие линейного динамического звена передаточная функция структурная схема временные характеристики динамического звена , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Понятие линейного динамического звена
САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов – динамических звеньев.
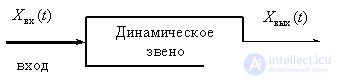
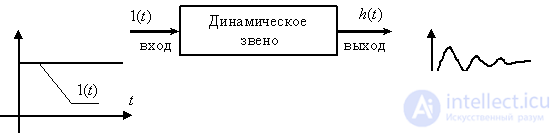
Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.
Рис. 1
Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.
Если уравнение, связывающее сигналы 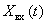
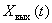
Уравнение линейного динамического звена имеет следующий общий вид:
|
|
(1) |
где 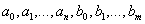
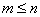
Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.
Передаточная функция
Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу
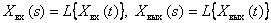
Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов
|
|
(2) |
Преобразуем уравнение (2) к следующему виду
|
|
(3) |
Получим из (3) отношение изображений выходного и входного сигналов
|
|
(4) |
Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (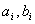
Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена
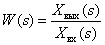
Уравнение вида
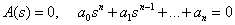
называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции – это характеристический полином дифференциального уравнения, описывающего динамическое звено.
Пример
Определим передаточную функцию динамического звена по его принципиальной электрической схеме
Рис . Об этом говорит сайт https://intellect.icu . 2
Решение:
По второму закону Кирхгоффа запишем уравнения описывающие схему
С учетом того, что
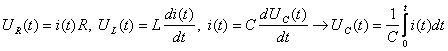
получаем
Получим операторные уравнения
Из второго уравнения выразим значение изображения тока
Подставим полученное выражение в первое уравнение системы
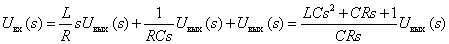
В итоге получаем искомую передаточную функцию
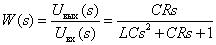
Структурная схема
Графически передаточные функции динамического звена представляют в следующем виде:
Рис. 3
Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях
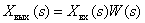
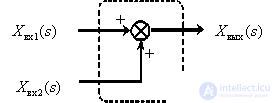
В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:
Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.
Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.
Пример
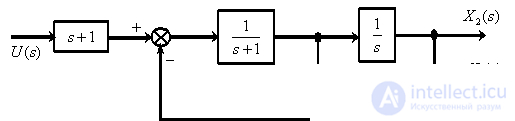
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Решение:
Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,
Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим
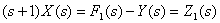
Тогда передаточная функция этого звена имеет вид
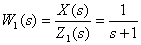
а выражение 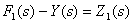
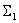
Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,
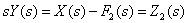
Тогда передаточная функция этого звена имеет вид
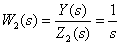
а выражение 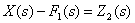
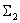
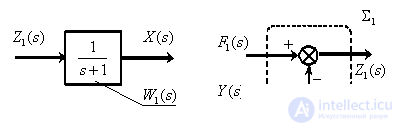
Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим
Временные характеристики динамического звена
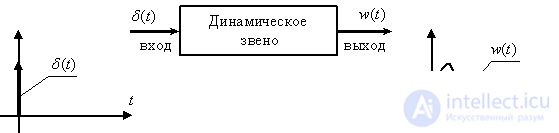
Временной или импульсной характеристикой динамического звена называют реакцию звена на 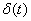
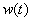
Рис. 4
Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?
Для этого рассмотрим динамическое звено с передаточной функцией
Рис. 5
В этом случае, в соответствии с (5), имеем
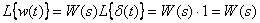
Таким образом
Получаем, что передаточная функция звена – это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции

при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.
Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.
Для динамического звена с передаточной функцией 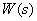

а если легко получить 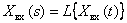
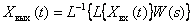
Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на 
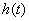
Рис. 6
Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией
Рис. 7
В этом случае, в соответствии с (5), имеем
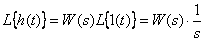
По теореме об интегрировании оригинала имеем
Переходная функция является интегралом по времени от импульсной характеристике и наоборот
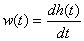
Переходная характеристика динамического звена может быть определена по передаточной функции
Контрольные вопросы и задачи
-
Что такое линейное динамическое звено?
-
Как определить передаточную функцию линейного динамического звена?
-
Перечислите основные элементы структурных схем систем управления.
-
Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?
-
Как по переходной характеристике определить импульсную характеристику динамического звена?
-
Определите передаточную функцию динамического звена по его принципиальной электрической схеме
Ответ:
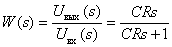
-
Определите передаточную функцию динамического звена по его принципиальной электрической схеме
Ответ:
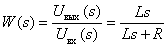
-
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Ответ:
На этом все! Теперь вы знаете все про понятие линейного динамического звена передаточная функция структурная схема временные характеристики динамического звена , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое понятие линейного динамического звена передаточная функция структурная схема временные характеристики динамического звена
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Математические основы теории автоматического управления
Ответы на вопросы для самопроверки пишите в комментариях,
мы проверим, или же задавайте свой вопрос по данной теме.
Найти передаточную функцию и дифференциальное уравнение пассивной электрической цепи
Понятие линейного динамического звена
САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов динамических звеньев.
Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.
Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.
Если уравнение, связывающее сигналы и , линейно, то говорят о линейном динамическом звене
Уравнение линейного динамического звена имеет следующий общий вид:
где — постоянные коэффициенты, .
Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.
Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу
.
Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов
Преобразуем уравнение (2) к следующему виду
Получим из (3) отношение изображений выходного и входного сигналов
Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (), имеет вид дробно-рациональной функции.
Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена
.
,
называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции это характеристический полином дифференциального уравнения, описывающего динамическое звено.
Определим передаточную функцию динамического звена по его принципиальной электрической схеме
По второму закону Кирхгоффа запишем уравнения описывающие схему
С учетом того, что
,
Получим операторные уравнения
Из второго уравнения выразим значение изображения тока
Подставим полученное выражение в первое уравнение системы
.
В итоге получаем искомую передаточную функцию
.
Графически передаточные функции динамического звена представляют в следующем виде:
Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях
.(5)
В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:
Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.
Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,
Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим
.
Тогда передаточная функция этого звена имеет вид
,
а выражение описывает суммирующее звено . Таким образом, получены два фрагмента структурной схемы
Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,
.
Тогда передаточная функция этого звена имеет вид
,
а выражение описывает суммирующее звено . Таким образом, получены еще два фрагмента структурной схемы
Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим
Временные характеристики динамического звена
Временной или импульсной характеристикой динамического звена называют реакцию звена на , обозначая ее как . При этом схема эксперимента имеет вид
Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?
Для этого рассмотрим динамическое звено с передаточной функцией
В этом случае, в соответствии с (5), имеем
.
Получаем, что передаточная функция звена это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции
,
при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.
Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.
Для динамического звена с передаточной функцией преобразуем (5), используя теорему об умножении изображений преобразования Лапласа,
,
а если легко получить , тогда
.
Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на , обозначая ее как . При этом схема эксперимента имеет вид
Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией
В этом случае, в соответствии с (5), имеем
.
По теореме об интегрировании оригинала имеем
Переходная функция является интегралом по времени от импульсной характеристике и наоборот
.
Переходная характеристика динамического звена может быть определена по передаточной функции
Контрольные вопросы и задачи
Что такое линейное динамическое звено?
Как определить передаточную функцию линейного динамического звена?
Перечислите основные элементы структурных схем систем управления.
Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?
Как по переходной характеристике определить импульсную характеристику динамического звена?
Определите передаточную функцию динамического звена по его принципиальной электрической схеме
.
Определите передаточную функцию динамического звена по его принципиальной электрической схеме
.
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Составление дифференциального уравнения заданной электрической цепи при заданном входном воздействии 10В и следующих исходных данных
Оглавление.
Составление дифференциального уравнения заданной электрической цепи при заданном входном воздействии 10В и следующих исходных данных. 5
Решение полученного дифференциального уравнения операторным способом, используя преобразования Лапласа. 6
Построение переходного процесса 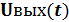
Запись выражений и построение частотных характеристик цепи. 9
Получение математического описания цепи в терминах пространства состояний. 13
Получение передаточной функции. 14
Получение дискретной передаточной функции. 14
Список литературы. 16
Введение
В данной работе проводилось исследование электрической цепи с применением математических методов.
В результате различных изменений состояния и параметров, возникают различные переходные процессы, которые являются следствием перераспределения энергии между элементами цепи.
В процессе работы было составлено дифференциальное уравнение, которое описывает входные и выходные параметры цепи, составлено уравнение в терминах пространства состояния, которое послужило проверкой для подтверждения правильности дифференциального уравнения, а также была получена функция в дискретном виде. Все эти виды записи описывают динамический процесс, происходящий в данной схеме электрической цепи.
Найденное дифференциальное уравнение было решено классическим методом и на основе полученного решения, был построен график переходного процесса. Описание в дискретной форме показывает наглядно, насколько различаются графики переходного процесса при разных временах дискретизации.
Для построения графиков использовалась программа MathCAD.
Операторный метод расчета переходных процессов
Содержание:
Операторный метод расчета переходных процессов:
Для решения линейных дифференциальных и интегродифференциальных уравнений в теории электрических цепей нашел широкое применение так называемый операторный метод, основанный на преобразованиях Лапласа.
Сущность этого метода заключается в том что функции вещественного переменного t преобразуются в функции комплексного переменного
Переход от функции вещественного переменного t к функции комплексного переменного p осуществляется с помощью прямого преобразования Лапласа
Обратный переход от функции комплексного переменного р к функциям вещественного переменного t осуществляется на основании обратного преобразования Лапласа
Функцию 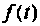
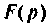
Напомним, что для того чтобы функция 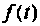
- удовлетворяла условиям Дирихле;
- была равна нулю для отрицательных значений t, т. е. при
- в интервале
не возрастала быстрее, чем некоторая показательная функция
где 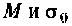
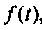
Применение свойств преобразования Лапласа в сочетании с теоремой разложения дает возможность составить таблицы изображений и оригиналов, облетающие и ускоряющие нахождение оригиналов по изображениям [4, 26]. Применение операторного метода совместно с компьютерными математическими программными средами делает анализ и расчет электрических цепей доступным, быстрым и интересным.
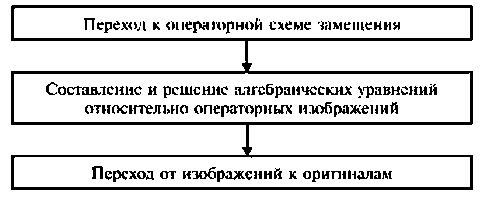
Особенностью метода является необходимость выполнения трех этапов:
Эквивалентные операторные схемы замещения элементов
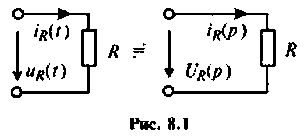
Активное сопротивление:
На рис. 8.1 изображена схема замещения в операторном виде участка цепи с активным сопротивлением. Для этого участка цепи связь между операторным напряжением и током записывается в виде
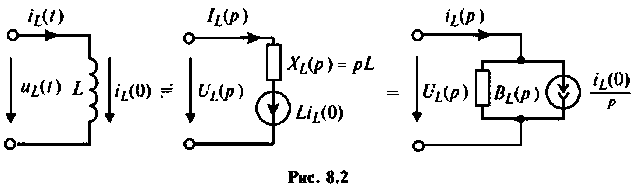
Индуктивность:
Для участка цепи с индуктивностью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.2.
Связь между операторным напряжением и током записывается в виде
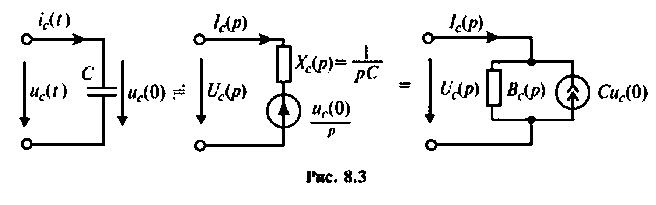
Емкость:
Для участка цепи с емкостью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.3.
Связь между напряжением и током устанавливает соотношение
В эквивалентных операторных схемах для индуктивности и емкости с ненулевыми начальными условиями возникают дополнительные источники ЭДС 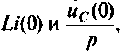
Порядок расчета:
- определяют независимые начальные условия;
- составляют эквивалентную операторную схему замещения для послекоммутационной цепи;
- составляют систему уравнений в операторной форме в соответствии с выбранным рациональным методом расчета эквивалентной схемы замещения и решают ее относительно изображений неизвестных величин;
- для нахождения оригиналов неизвестных величин используют таблицы соответствия, формулы теоремы разложения, компьютерные программные среды и др.
Операторные функции электрических цепей
Основные операторные функции:
Операторной функцией цепи называется отношение изображения по Лапласу выходной величины 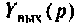
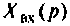
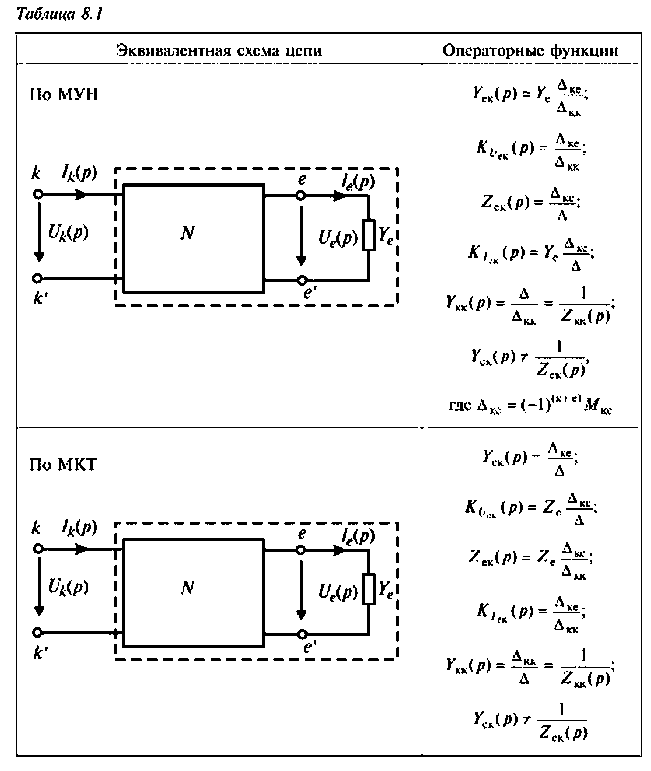
Операторная функция зависит только от параметров цепи и ее схемы. Различают входные и передаточные операторные функции. В табл. 8.1 приведены соотношения для расчета операторных функций сложных цепей.
Для расчета операторных функции можно применять все методы расчета комплексных функций
т. е. комплексная функция является частным случаем операторной при замене оператора 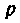
Анализ переходных процессов в цепях с помощью операторных функций
По известной операторной функции цепи и операторному изображению воздействия можно найти реакцию цепи на это воздействие
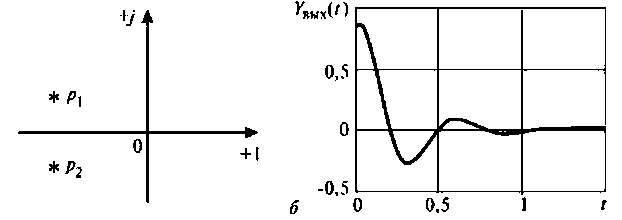
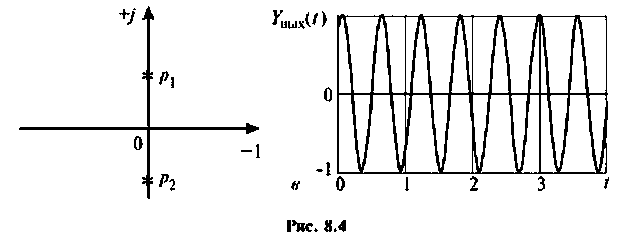
На рис. 8.4 (а—в) приведены временные диаграммы переходных процессов, а также полюсно-нулевое представление на комплексной плоскости.
По расположению полюсов операторной функции можно судить о характере переходное процесса:
- если все полюсы расположены только на отрицательной вещественной полуоси, то переходный процесс в цепи носит апериодический характер;
- если имеются сопряженные полюсы в левой полуплоскости, то переходный процесс носит характер затухающих колебаний;
- если все полюсы расположены только на отрицательной мнимой оси, то переходный процесс в цепи носит характер незатухающих колебаний.
Примеры решения задач
Пример 8.4.1.
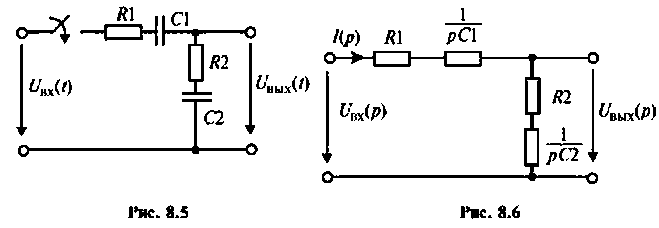
В интегродифференцирующем контуре постоянного тока (рис. 8.5), применяемом для коррекции ЭЦ и САУ. определить напряжение 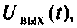
Решение
Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало:
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.6).
Находят изображение напряжения 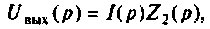
Сопротивление всей цепи определяется выражением
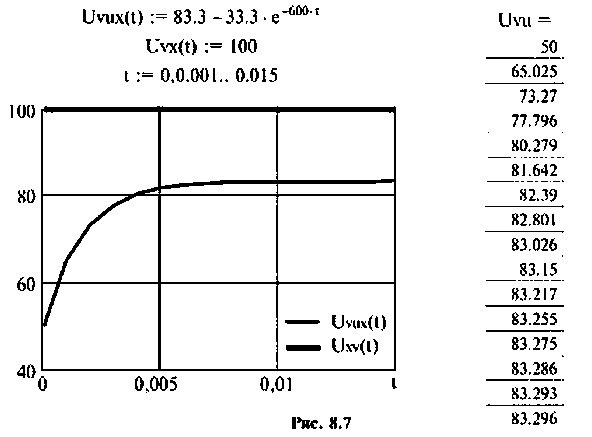
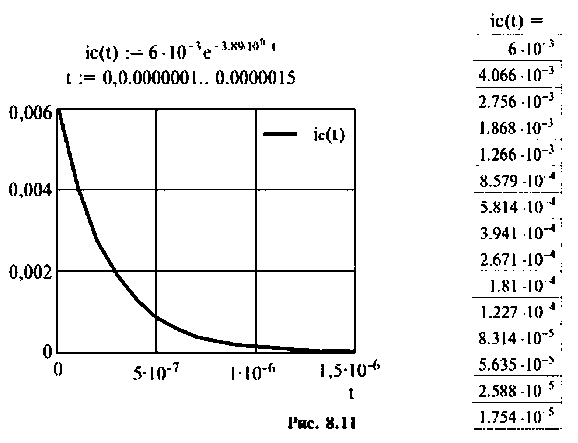
По данному изображению находят оригинал (рис. 8.7) напряжения 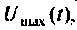
Пример 8.4.2.
К пассивному RС-фильтру нижних частот подключается нагрузка 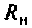
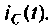
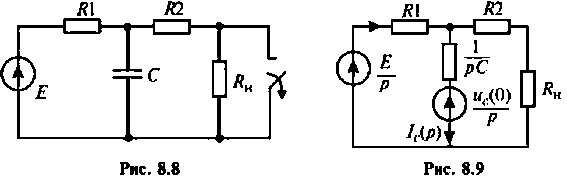
Дано:
Решение
Определяют независимые начальные условия — напряжение на емкости
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.9).
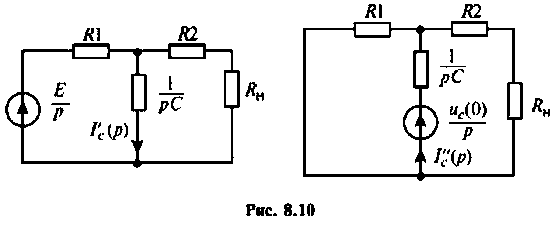
Операторный ток 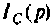
Операторные схемы, соответствующие частичным токам, изображены на рис. 8.10.
Искомый ток
Определяют частичный ток
Аналогично определяют частичный ток
По данному изображению 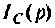
Подставляя числовые значения величин, получают
Строят график тока 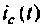
Выводы. До коммутации напряжение на емкости определялось падением напряжения на сопротивлении 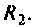
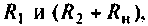
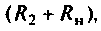
Пример 8.4.3.
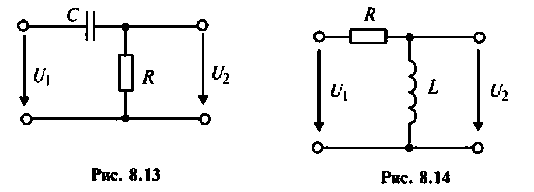
Рассчитать коэффициент передачи по напряжению пассивной цепи (рис. 8.12) и составить ее схему так, чтобы при подключении на вход источника постоянной ЭДС 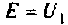
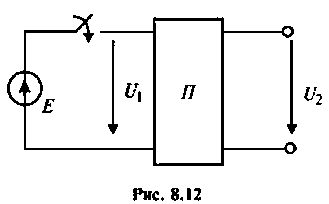
Решение
Применяя преобразования Лапласа, находят изображения
Из прямых преобразований Лапласа и Фурье следует, что
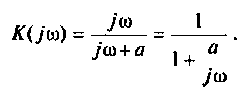
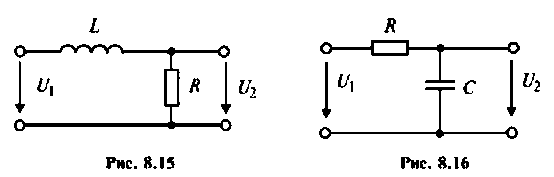
Если принять 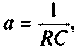
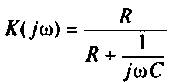
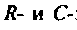
Если принять 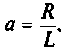
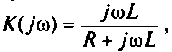
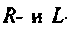
Если принять 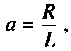
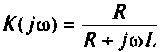
Если принять 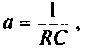
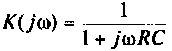
Пример 8.4.4.
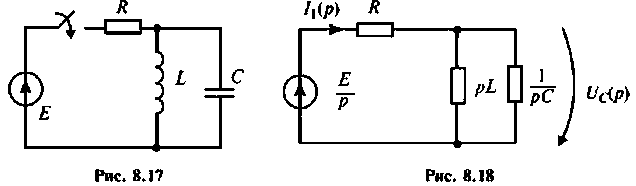
Параллельный колебательный контур (рис. 8.17) включается на постоянное напряжение
Определить напряжение на конденсаторе и построить его опюру, если:
Решение
Определяют независимые начальные условия: напряжение на конденсаторе 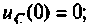
Строят эквивалентную операторную схему замещения после коммутации (рис. 8.18).
Находят изображение напряжения на конденсаторе
По данному изображению находят оригинал по теореме разложения дробно-рациональной функции
где 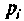
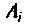
При простых (некратных) полюсах 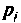
а) Для первого варианта значений:
Полюсы изображения 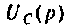
Вычисляют производную 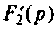
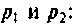
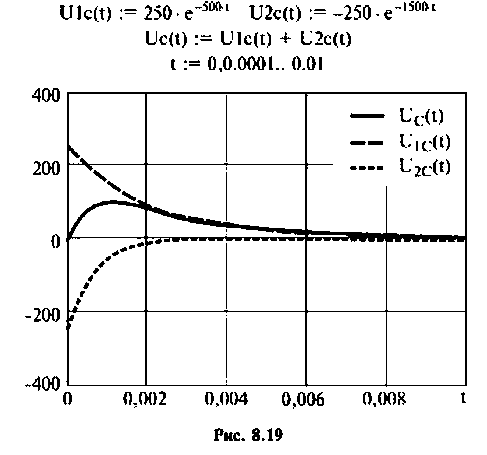
Вычисляют начальные значения компонент
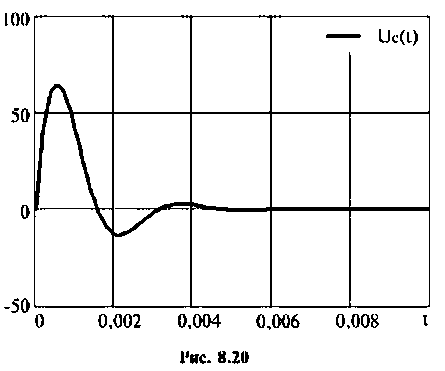
Графики напряжения на конденсаторе и его компонентов получены в среде Mathcad и показаны на рис. 8.19.
Тоn же результат может быть получен по таблице преобразования Лапласа (табл. 8.2, п. 8), если знаменатель изображения напряжения на конденсаторе представить в виде
б) Для второго варианта числовых значений:
а полюсы
Находят производную от 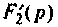
По теореме разложения определяют
где
или
График изменения напряжения 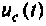
Тот же результат может быть получен по таблице преобразования Лапласа (см. табл. 8.2, п. 13), если знаменатель 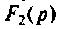
Примечание. Результаты этого примера сравните с результатами примера 6.3. Оцените достоинства и недостатки классического и операторного методов расчета переходных процессов.
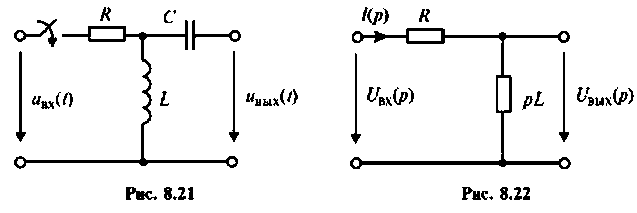
Пример 8.4.5.
После замыкания ключа четырехполюсник (рис. 8.21) используется для работы на частоте
а) коэффициент передачи по напряжению 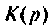
б) характер переходного процесса по кривой переходного процесса.
Дано:
Решение
В режиме холостого хода
Изображают эквивалентную операторную схему замещения. На рис. 8.22 приведена операторная схема замещения при нулевых начальных условиях.
Находят изображение напряжения на выходе
Определяют полюсы операторной функции из уравнения 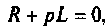
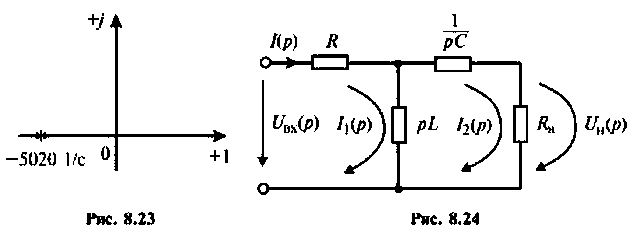
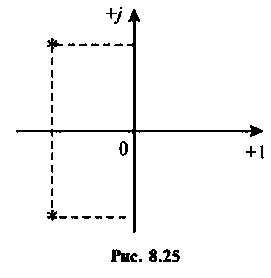
Переходной процесс в цепи имеет апериодический характер, что видно из расположения полюсов на комплексной плоскости (рис, 8.23).
В режиме нагрузки
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.24).
Определяют операторную функцию 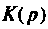
Определяют полюсы операторной функции из уравнения
Для этога вначале вычисляют L и С.
Находят корни уравнения:
Переходный процесс в цепи имеет характер затухающих колебаний, что видно из расположения полюсов на комплексной плоскости (рис. 8.25).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://mydocx.ru/11-55509.html
http://www.evkova.org/operatornyij-metod-rascheta-perehodnyih-protsessov









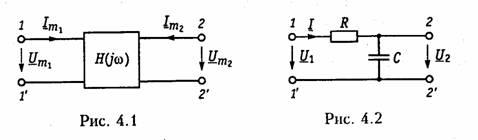

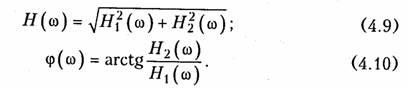
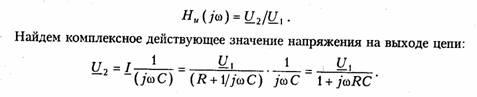





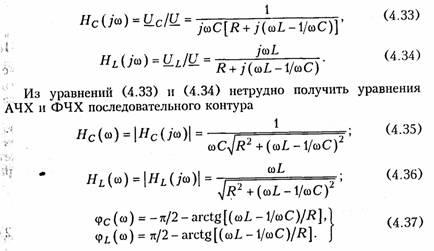
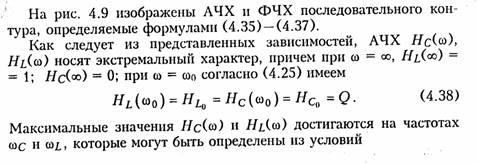

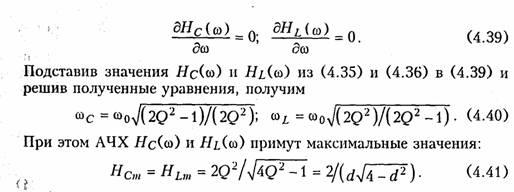
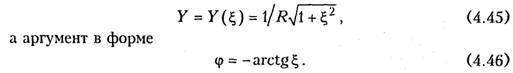

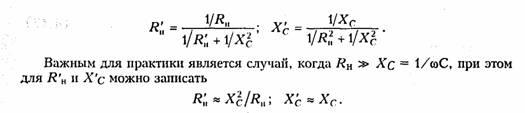
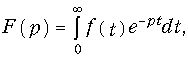
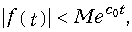
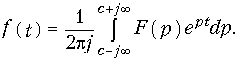
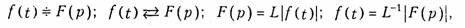
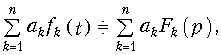
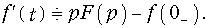
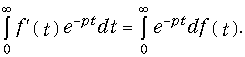
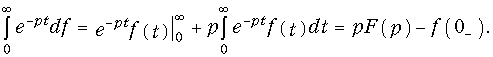
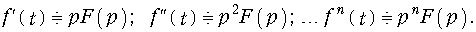
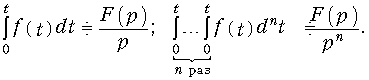
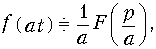
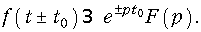
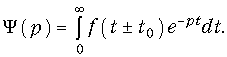
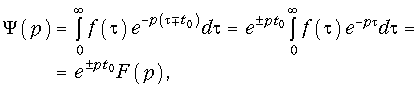
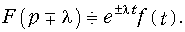
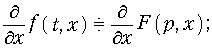
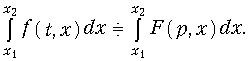
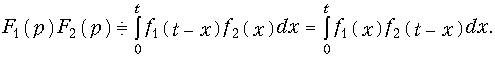
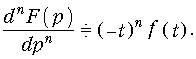
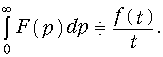
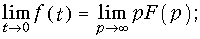
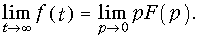

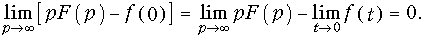
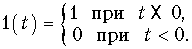
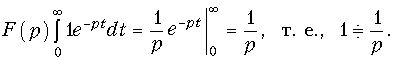
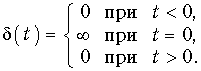

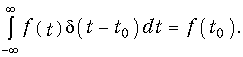
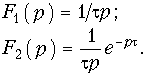
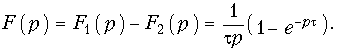
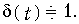
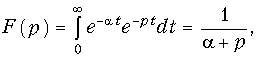
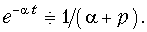
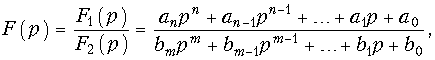
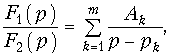
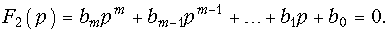
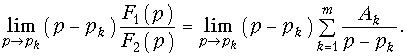
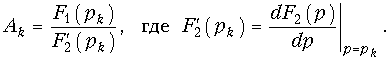
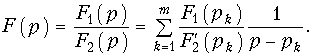
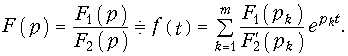
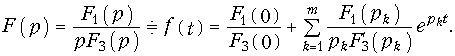
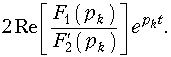
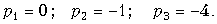
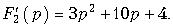
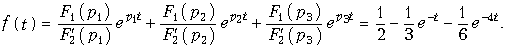
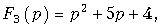
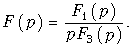
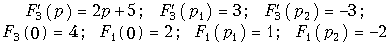
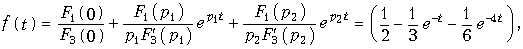
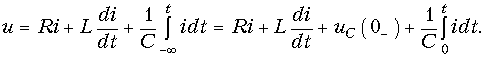
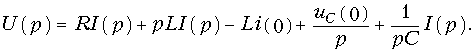
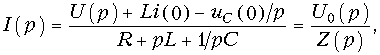
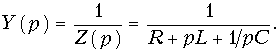
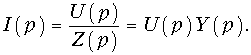
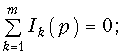
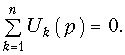
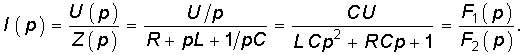
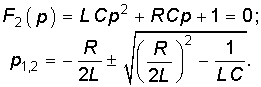
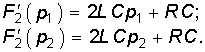
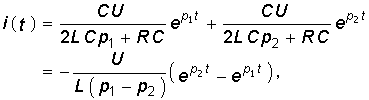
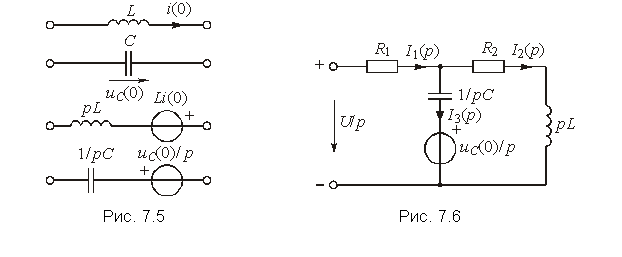
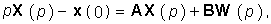
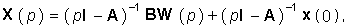
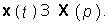
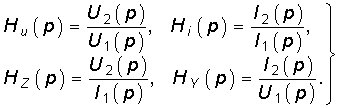
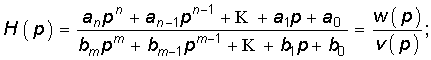
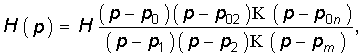
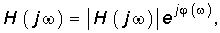
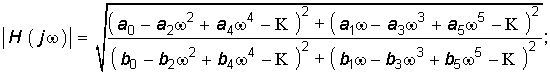
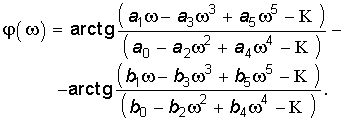
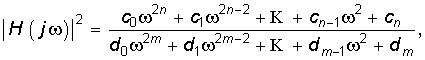
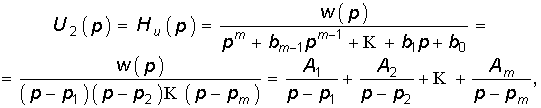
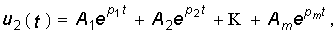
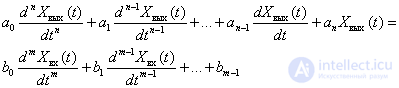
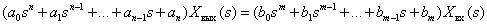
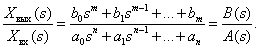

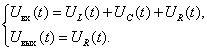
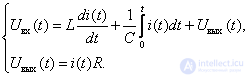
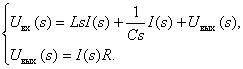

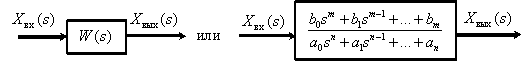
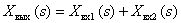
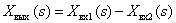



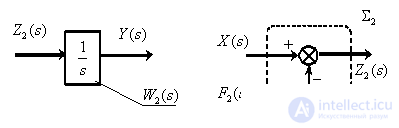

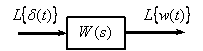
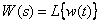
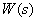
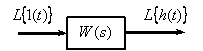
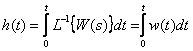
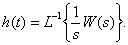


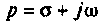
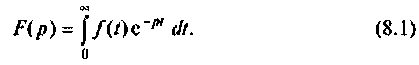
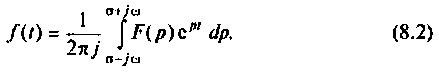
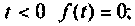
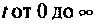 не возрастала быстрее, чем некоторая показательная функция
не возрастала быстрее, чем некоторая показательная функция