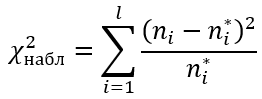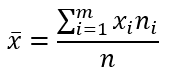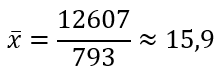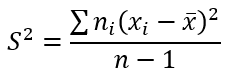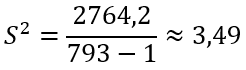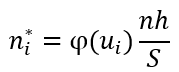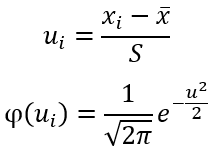До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
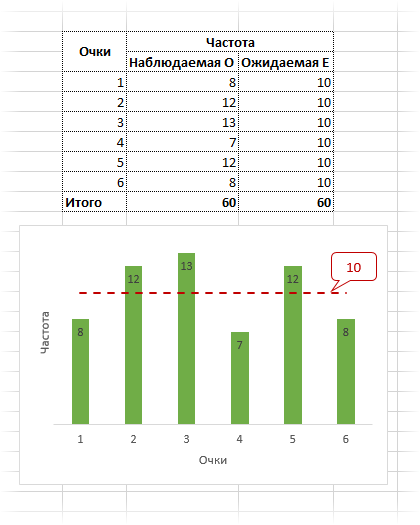
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
Это и есть статистика для критерия Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.
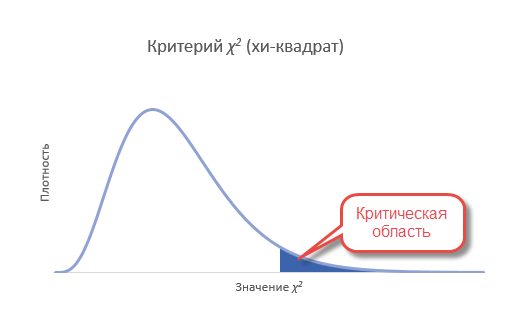
«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
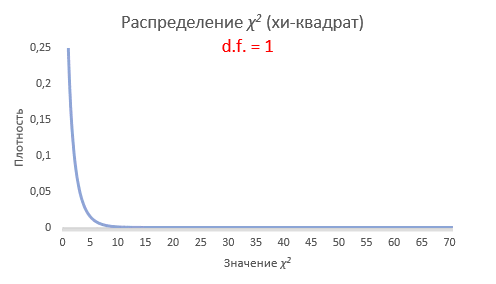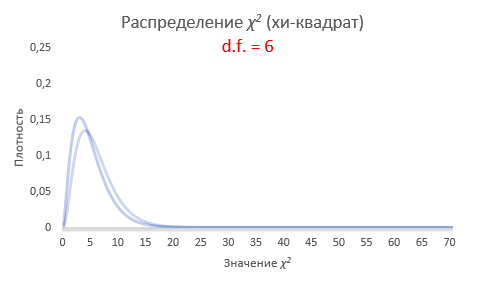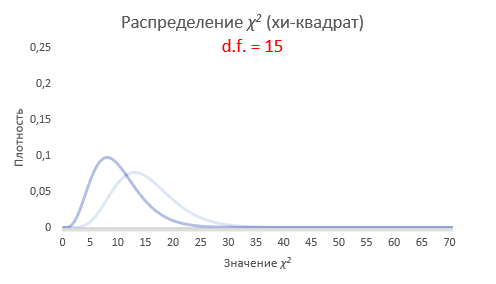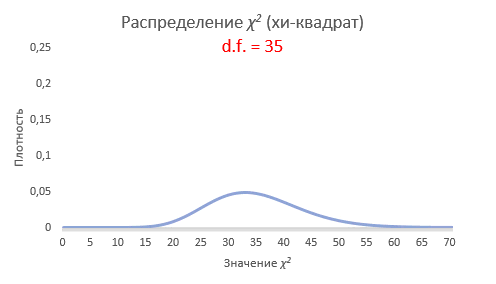
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Проверка гипотезы по критерию Хи квадрат Пирсона
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.
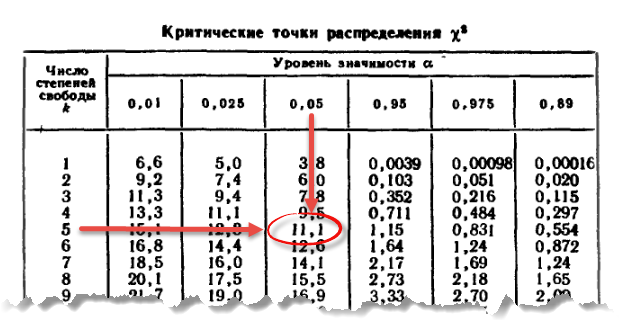
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
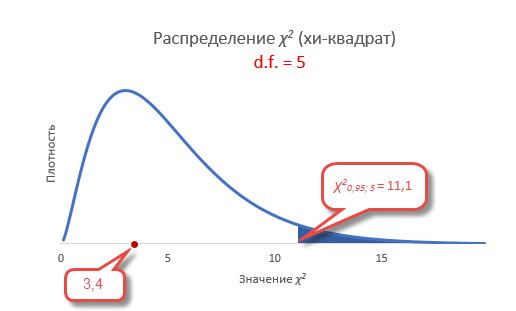
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
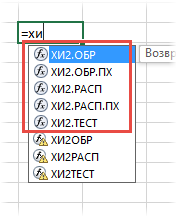
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)
ХИ2.ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
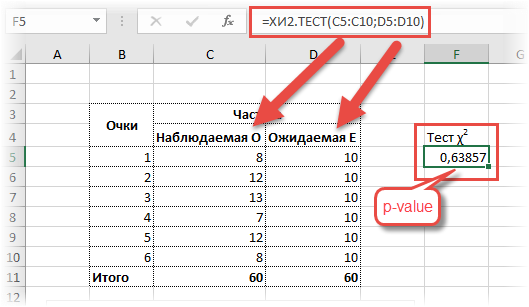
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
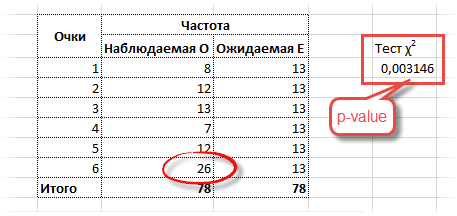
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
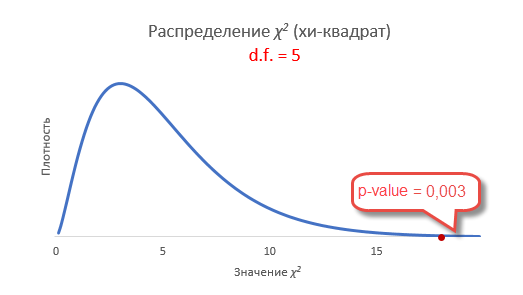
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях:
Решения задач на проверку статистических гипотез
Проверка статистических гипотез включает в себя большой пласт задач математической статистики. Зная некоторые характеристики выборки (или имея просто выборочные данные), мы можем проверять гипотезы о виде распределении случайной величины или ее параметрах (примеры этих задач на странице Проверка гипотез о параметрах распределения).
Ниже в примерах мы разберем основные учебные задачи на проверку гипотез о виде распределения. Чаще всего для этого используется критерий согласия $chi^2$ Пирсона, а также критерий Колмогорова-Смирнова.
Критерий согласия Пирсона (или критерий $chi^2$ — «хи квадрат») — наиболее часто употребляемый для проверки гипотезы о принадлежности некоторой выборки теоретическому закону распределения (в учебных задачах чаще всего проверяют «нормальность» — распределение по нормальному закону).
В учебных задачах обычно используется следующий алгоритм:
- Выбор теоретического закона распределения (обычно задан заранее, если не задан — анализируем выборку, например с помощью гистограммы относительных частот, которая имитирует плотность распределения).
- Оцениваем параметры распределения по выборке (для этого вычисляется математическое ожидание и дисперсия): $a, sigma$ для нормального, $a,b$ — для равномерного, $lambda$ — для распределения Пуассона и т.д.
- Вычисляются теоретические значения частот (через теоретические вероятности попадания в интервал) и сравниваются с исходными (выборочными).
- Анализируется значение статистики $chi^2$ и делается вывод о соответствии (или нет) теоретическому закону распределения.
Подробные примеры на разные распределения и критерии вы найдете ниже.
Лучшее спасибо — порекомендовать эту страницу
Примеры решений на проверку гипотез онлайн
Критерий Пирсона, нормальное распределение
Пример 1. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X по результатам выборки:
X 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,1 2,3
N 7 9 28 27 30 26 21 25 22 9 5
Пример 2. Были исследованы 200 готовых деталей на отклонения истинного размера от расчетного. Сгруппированные данные приведены в следующей таблице:
По данному статистическому ряду построить гистограмму. По виду гистограммы выдвинуть гипотезу о виде закона распределения (например, предположить, что исследуемая величина имеет нормальный закон распределения). Подобрать параметры закона распределения (равные их оценкам на основе опытных данных). На том же графике построить функцию плотности вероятности, соответствующую выдвинутой гипотезе. С помощью критерия согласия проверить, согласуется ли гипотеза с опытными данными. Уровень значимости взять, например, равным 0,05.
Критерий Пирсона, распределение по закону Пуассона
Пример 3. Отдел технического контроля проверил n партий однотипных изделий и установил, что число нестандартных изделий в одной партии имеет эмпирическое распределение, приведенное в таблице, в одной строке которой указано количество xi нестандартных изделий в одной партии, а в другой строке – количество ni партий, содержащих xi нестандартных изделий. Требуется при уровне значимости α0,05 проверить гипотезу о том, что случайная величина X (число нестандартных изделий в одной партии) распределена по закону Пуассона.
Пример 4. В результате обследования 150 человек были получены данные о количестве приобретаемых за месяц цветных иллюстрированных журналов. Соответствует ли данное распределение закону редких событий Пуассона?
Критерий Пирсона, распределение по показательному закону
Пример 5. В итоге испытаний 1000 элементов на время безотказной работы (час.) получено распределение, приведенное в таблице. Требуется при уровне значимости проверить гипотезу о том, что данные в генеральной совокупности распределены по показательному закону.
Время безотказной работы 0-10 10-20 20-30 30-40 40-50 50-60 60-70
Число отказавших элементов 365 245 150 100 70 45 25
Критерий Пирсона, распределение по равномерному закону
Пример 6. В некоторой местности в течение 300 суток регистрировалась среднесуточная температура воздуха. В итоге наблюдений было получено эмпирическое распределение, приведенное в таблице 40 (в первом столбце указан интервал температуры в градусах, во втором столбце – частота $n_i$, т.е. количество дней, среднесуточная температура которых принадлежит этому интервалу).
Требуется при уровне значимости 0,05 проверить гипотезу о том, что среднесуточная температура воздуха распределена равномерно.
Критерий Колмогорова
Пример 7. Имеются выборочные данные о числе сделок, заключенных фирмой с частными лицами в течение месяца:
— число заключенных сделок 0-10 10-20 20-30 30-40 40-50
— число частных лиц 23 24 11 9 3
Проверить при уровне значимости 0,05, используя критерий согласия Колмогорова, гипотезу о нормальном законе распределения.
Пример 8. В течение месяца выборочно осуществлялась проверка торговых точек города по продаже овощей. Результаты двух проверок по недовесам покупателям одного вида овощей приведены в таблице:Можно ли считать при уровне значимости 0,05, что недовесы овощей являются устойчивым и закономерным процессом при продаже овощей в данном городе (т.е. описываются одной и той же функцией распределения)?
Критерий Вилкоксона
Пример 9. Имеется выборка прибыли коммерческой фирмы за 14 недель до (хi) и после (yi) проведения новой экономической политики. На уровне значимости 0,05 по критерию Вилкоксона проверить гипотезу о том, что введение новой экономической политики в среднем привело к увеличению производительности.
Критерий $chi^2$ для двух выборок
Пример 10. Используя критерий «хи-квадрат» при уровне значимости 0,05, проверить, существует ли зависимость уровня интеллектуального развития учеников от типа школы по результатам обследования 100 сельских и 100 городских школьников:
Тип школы Уровень интеллектуального развития
низкий нормальный высокий
Городская 25 50 25
Сельская 52 41 7
Нужно решить задачи на проверку статистических гипотез?
Полезные ссылки
- Критерий согласия Пирсона Хи-квадрат
- Критерий согласия для распределения Пуассона и нормального
- Решение задач на заказ
- Ссылки на учебники
- Решенные контрольные
Решебник по математической статистике
Ищете решенное задание на проверку статистических гипотез? Попробуйте тут:
Критерий согласия Пирсона (или хи-квадрат) вычисляется по формуле:
ni – эмпирические частоты;
ni* – теоретические частоты;
l – количество интервалов (вариант)
Объем выборки по критерию Пирсона:
n>30
Теоретические частоты должны быть больше 5.
Распределение Пирсона с k степенями свободы рассчитывается по формуле:
k=l−r−1
r – число параметров предполагаемого распределения
Если предполагаемое распределение имеет нормальный закон распределения, то число степеней свободы оценивают по двум параметрам (математическое ожидание и СКО) и формула имеет вид:
k=l−3
Пример
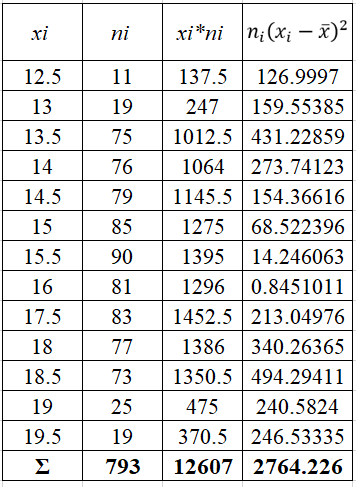
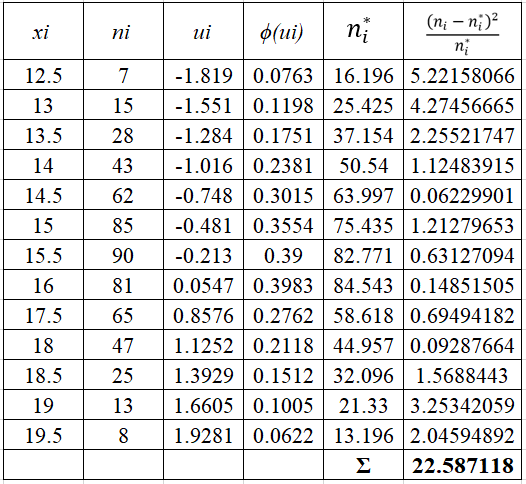
Проверить гипотезу о нормальном распределении по критерию Пирсона при уровне значимости 0,01. Дана выборка данных измерений в виде таблицы
Найдем выборочное среднее по формуле:
Отсюда
Формула выборочной исправленной дисперсии:
Тогда
Откуда получаем выборочную исправленную СКО:
Получаем параметры нормального распределения mx=15,9, σ=1,87.
Найдем теоретические частоты по формуле:
h – шаг между вариантами, h=0,5
При уровне значимости α=0,01 и число степеней свободы k=13−3=10 по таблице Пирсона найдем критическое значение:
Наблюдаемое значение критерия равно:
Ввиду того, что
следовательно, нулевую гипотезу о нормальном распределении принимаем.
14748
Проверка гипотезы о показательном распределении генеральной совокупности
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть
эмпирическое распределение непрерывной случайной величины
задано в виде последовательности интервалов
и соответствующих им частот
.
Требуется, используя критерий Пирсона, проверить
гипотезу о том, что случайная величина
имеет показательное распределение.
Для того
чтобы при уровне значимости
проверить гипотезу о том, что непрерывная
случайная величина распределена по показательному закону, надо:
1.
Вычислить выборочную среднюю
, причем в качестве вариант
принимают среднее арифметическое концов
интервала:
2. Принять в качестве оценки параметра
показательного распределения величину,
обратную выборочной средней:
3. Найти вероятности попадания
в частичные интервалы
по формуле:
4. Вычислить
теоретические частоты:
где
– объем выборки
5.
Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для
этого:
а)
составляют расчетную таблицу (см. пример), по которой находят наблюдаемое
значение критерия
б) по
таблице критических точек распределения
, по заданному уровню
значимости
и числу степеней свободы
(
– число групп выборки) находят критическую
точку
правосторонней критической области.
Если
– нет оснований отвергнуть гипотезу о
нормальном распределении генеральной совокупности. Если
— гипотезу отвергают.
Замечание.
Малочисленные частоты
следует объединить, в этом случае и
соответствующие им теоретические частоты также надо сложить. Если производилось
объединение частот, то при определении числа степеней свободы по формуле
следует в качестве
принять число групп выборки, оставшихся после
объединения частот.
Примеры решения задач
Пример 1
Для случайной величины X составить интервальный
вариационный ряд, вычислить выборочные средние характеристики, подобрать
теоретический закон распределения, проверить его согласование с теоретическим
критерием Пирсона при α=0,05.
| 15 | 22 | 33.5 | 25 | 9 | 4.2 | 12.5 | 60 | 41 | 5 |
| 16.8 | 10.2 | 35 | 49 | 19 | 18 | 20 | 40 | 5 | 14.2 |
| 2.5 | 2 | 3.5 | 18.1 | 18.9 | 2.3 | 38.2 | 28.7 | 5 | 21.5 |
| 25.5 | 6.8 | 4.8 | 6.5 | 18.3 | 22.5 | 0.5 | 55.5 | 21.5 | 75 |
| 30 | 7 | 45 | 28 | 24 | 15 | 46.5 | 32 | 30 | 8.5 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Разобьем
заданную совокупность значений на непересекающиеся и примыкающие друг к другу
интервалы.
Размах
вариации равен:
Величину
интервала определим по формуле:
Подсчитаем количество значений заданной
совокупности, попадающее в соответствующий интервал. Получаем следующее
интервальное распределение.
Вычислим характеристики распределения. Для этого
составим расчетную таблицу. В качестве величины х возьмем середины интервалов.
Выборочная
средняя:
Вычислим
выборочную дисперсию.
Средняя
квадратов:
Выборочная
дисперсия:
Среднее
квадратическое отклонение:
Найдем оценку параметра предполагаемого
показательного распределения:
Найдем вероятности попадания случайной величины х в
каждый из интервалов по формуле:
Теоретические частоты:
, где
-объем выборки
Составим расчетную таблицу:
Проверим степень согласия эмпирического и
теоретического распределения по критерию Пирсона. Объединяем малочисленные
частоты (n<5).
Из
расчетной таблицы
Уровень
значимости
Число
степеней свободы
По
таблице критических точек распределения:
Гипотеза
о распределении случайной величины по показательному закону подтверждается.
Пример 2
При уровне значимости α = 0,01 проверить
гипотезу о показательном законе распределения признака X генеральной совокупности по выборке, данные которой
приведены в таблице:
| xi | 3.0-3.6 | 3.6-4.2 | 4.2-4.8 | 4.8-5.4 | 5.4-6.0 | 6.0-6.6 | 6.6-7.2 |
| ni | 43 | 35 | 22 | 15 | 8 | 5 | 2 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим расчетную таблицу
| Интервалы |
Середина интервала,
|
|
|
| 3 – 3.6 | 3.3 | 43 | 141.9 |
| 3.6 – 4.2 | 3.9 | 35 | 136.5 |
| 4.2 – 4.8 | 4.5 | 22 | 99.0 |
| 4.8 – 5.4 | 5.1 | 15 | 76.5 |
| 5.4 – 6 | 5.7 | 8 | 45.6 |
| 6 – 6.6 | 6.3 | 5 | 31.5 |
| 6.6 – 7.2 | 6.9 | 2 | 13.8 |
| Итого | — | 130 | 544.8 |
Средняя:
Оценка
параметра предполагаемого показательного распределения:
Теоретические
частоты находим по формуле:
Получаем:
Сравним
эмпирические и теоретические частоты с помощью критерия Пирсона. Объединим
малочисленные частоты
и соответствующие им теоретические:
|
Интервалы,
|
|
|
|
| 3 – 3.6 | 43 | 74.9 | 13.6 |
| 3.6 – 4.2 | 35 | 7.3 | 105.1 |
| 4.2 – 4.8 | 22 | 6.4 | 38.0 |
| 4.8 – 5.4 | 15 | 5.5 | 16.4 |
| 5.4 – 6 | 8 | 4.9 | 2.0 |
| 6 – 7.2 | 7 | 31 | 18.6 |
| Итого | 130 | 130 | 193.7 |
Из расчетной таблицы
Уровень значимости
Число степеней свободы
По таблице критических точек
распределения:
Гипотезу о распределении случайной
величины по показательному закону отвергаем.
Задачи контрольных и самостоятельных работ
Задача 1
По
заданной выборке случайной величины
вычислить основные эмпирические
характеристики:
—
выборочную среднюю;
—
выборочную дисперсию;
—
исправленное значение выборочной дисперсии;
— среднее
квадратическое отклонение;
— построить
доверительный интервал для оценки математического ожидания. Считать надежность
оценки равной 0,95;
—
построить доверительный интервал для оценки дисперсии. Считать надежность
оценки равной 0,95.
—
построить по данным выборки полигон и гистограмму. Подобрать подходящий
теоретический закон распределения вероятностей. Проверить гипотезу о
соответствии эмпирического закона распределения выбранному теоретическому при
уровне значимости α=0.05.
| 0 | 0.4 | 1.5 | 0.7 | 2.9 | 0.3 | 2.1 | 0.6 | 0.2 | 0.3 |
| 7.4 | 0.2 | 0.1 | 1.3 | 1.5 | 0.3 | 1 | 0.1 | 2.5 | 1.2 |
| 3.5 | 5.2 | 1.3 | 1 | 3.3 | 2.5 | 9.6 | 1.6 | 0.5 | 3.1 |
| 0.8 | 1.9 | 0 | 0.5 | 1.5 | 2.1 | 3 | 2.3 | 1 | 2.3 |
| 1.5 | 2.2 | 1.4 | 0.3 | 0.9 | 1.2 | 2.3 | 0.3 | 1.1 | 2 |
| 0.2 | 1.3 | 0.4 | 0.1 | 6.2 | 4.4 | 1.4 | 0.9 | 1.7 | 0.5 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Распределение 200 элементов
(устройств) по времени безотказной работы (в часах) представлено в таблице:
|
|
0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
|
|
133 | 45 | 15 | 4 | 2 | 1 |
На уровне
значимости 0.05 проверить гипотезу о показательном законе распределения
признака (случайной величины) X, используя критерий χ2
–Пирсона.
Задача 3
Для
изучения качества транзисторов на продолжительность их работы в часах было
выборочно проведено обследование транзисторов.
Требуется:
1.
Составить интервальный статистический ряд частот и частостей случайной величины
X -продолжительности работы транзисторов.
2.
Построить гистограмму и полигон частостей.
3. Найти
выборочные величины
.
4.
Обосновать гипотезу о распределении исследуемой величины по показательному
закону.
5.
Написать формулу плотности вероятности предполагаемого закона.
6.
Проверить степень согласия теоретического и эмпирического распределений с
помощью критерия χ2 Пирсона при уровне значимости α=0.05.
| 44 | 78 | 22 | 32 | 144 | 33 | 11 | 41 | 280 | 12 |
| 10 | 11 | 41 | 140 | 52 | 155 | 40 | 22 | 12 | 66 |
| 72 | 18 | 10 | 22 | 133 | 12 | 92 | 44 | 104 | 88 |
| 49 | 21 | 62 | 51 | 21 | 92 | 68 | 49 | 122 | 29 |
| 30 | 29 | 31 | 21 | 30 | 41 | 42 | 29 | 30 | 31 |
| 52 | 68 | 44 | 22 | 320 | 52 | 20 | 20 | 71 | 11 |
| 40 | 9 | 18 | 7 | 92 | 78 | 112 | 32 | 22 | 92 |
| 42 | 5 | 6 | 45 | 25 | 46 | 111 | 71 | 21 | 31 |
| 31 | 35 | 45 | 102 | 30 | 31 | 6 | 82 | 48 | 46 |
| 65 | 18 | 25 | 20 | 98 | 4 | 11 | 84 | 9 | 10 |
Задача 4
Даны
результаты испытания прибора на продолжительность работы T (ч.)
Требуется:
1.
Составить интервальный статистический ряд.
2.
Построить полигон и гистограмму распределения.
3.
Подобрать закон распределения испытуемой СВ.
4. Найти
точечные оценки параметров распределения.
5.
Проверить на уровне значимости α=0.05 гипотезу о выдвинутом законе
распределения.
| 25 | 125 | 440 | 514 | 24 | 0 | 333 | 700 | 48 | 543 |
| 525 | 1240 | 990 | 800 | 413 | 700 | 511 | 630 | 241 | 25 |
| 1100 | 810 | 800 | 432 | 68 | 420 | 1020 | 48 | 0 | 140 |
| 25 | 85 | 67 | 420 | 1560 | 920 | 647 | 1800 | 1120 | 31 |
| 1020 | 2640 | 84 | 448 | 900 | 24 | 88 | 900 | 1631 | 35 |
| 754 | 820 | 1120 | 3000 | 1600 | 1300 | 2010 | 18 | 162 | 1610 |
| 25 | 444 | 34 | 400 | 32 | 920 | 1654 | 2140 | 965 | 750 |
| 550 | 1200 | 14 | 417 | 17 | 0 | 81 | 41 | 411 | 1320 |
| 1640 | 1200 | 600 | 420 | 1300 | 25 | 3 | 24 | 120 | 1110 |
| 700 | 7 | 1111 | 2008 | 953 | 1050 | 125 | 1300 | 720 | 34 |
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Критерий Пирсона.
Достоинством
критерия Пирсона является его
универсальность: с его помощью можно
проверять гипотезы о различных законах
распределения.
1.
Проверка гипотезы о нормальном
распределении. Пусть
получена выборка достаточно большого
объема п
с большим количеством различных значений
вариант. Для удобства ее обработки
разделим интервал от наименьшего до
наибольшего из значений вариант на s
равных частей и будем считать, что
значения вариант, попавших в каждый
интервал, приближенно равны числу,
задающему середину интервала. Подсчитав
число вариант, попавших в каждый интервал,
составим так называемую сгруппированную
выборку:
варианты………..х1
х2
… хs
частоты………….п1
п2
… пs
,
где хi
– значения середин интервалов, а пi
– число вариант, попавших в i-й
интервал (эмпирические частоты). По
полученным данным можно вычислить
выборочное среднее
и выборочное среднее квадратическое
отклонение σВ.
Проверим предположение, что генеральная
совокупность распределена по нормальному
закону с параметрами M(X)
=
,
D(X)
=
.
Тогда можно найти количество чисел из
выборки объема п,
которое должно оказаться в каждом
интервале при этом предположении (то
есть теоретические частоты). Для этого
по таблице значений функции Лапласа
найдем вероятность попадания в i-й
интервал:
,
где аi
и bi
— границы
i-го
интервала. Умножив полученные вероятности
на объем выборки п, найдем теоретические
частоты: пi
=n·pi.
Наша цель –
сравнить эмпирические и теоретические
частоты, которые, конечно, отличаются
друг от друга, и выяснить, являются ли
эти различия несущественными, не
опровергающими гипотезу о нормальном
распределении исследуемой случайной
величины, или они настолько велики, что
противоречат этой гипотезе. Для этого
используется критерий в виде случайной
величины

(7)
Смысл ее очевиден:
суммируются части, которые квадраты
отклонений эмпирических частот от
теоретических составляют от соответствующих
теоретических частот. Можно доказать,
что вне зависимости от реального закона
распределения генеральной совокупности
закон распределения случайной величины
(7) при
стремится к закону распределения
с числом степеней свободы k
= s
– 1 – r,
где r
– число
параметров предполагаемого распределения,
оцененных по данным выборки. Нормальное
распределение характеризуется двумя
параметрами, поэтому k
= s
– 3. Для
выбранного критерия строится правосторонняя
критическая область, определяемая
условием
(8)
где α
– уровень значимости. Следовательно,
критическая область задается неравенством
а область принятия гипотезы —
.
Итак, для проверки
нулевой гипотезы Н0:
генеральная совокупность распределена
нормально – нужно вычислить по выборке
наблюдаемое значение критерия:
,
(7`)
а по таблице
критических точек распределения χ2
найти критическую точку
,
используя известные значения α и k
= s
– 3. Если
— нулевую гипотезу принимают, при
ее отвергают.
Пример.
Результаты исследования спроса на товар
представлены в таблице:
|
Стоимость, руб. |
120–160 |
160–180 |
180–200 |
200–220 |
220–280 |
|
Кол-во, шт. |
5 |
10 |
14 |
12 |
9 |
Выдвинуть
гипотезу о виде распределения и проверить
её на уровне значимости =0,01.
I. Выдвижение
гипотезы.
Для указания вида
эмпирического распределения построим
гистограмму
120
160 180 200 220 280
По
виду гистограммы можно сделать
предположение о нормальном законе
распределения изучаемого признака в
генеральной совокупности.
II.
Проверим выдвинутую гипотезу о нормальном
распределении, используя критерий
согласия Пирсона.
1.
Вычисляем
,
В.
В
качестве вариант возьмём среднее
арифметическое концов интервалов:
;
.
2.
Найдём интервалы (Zi;
Zi+1):
;
.
За
левый конец первого интервала примем
(-),
а за правый конец последнего интервала
— (+).
Результаты представлены в табл. 4.
3.
Найдем теоретические вероятности Рi
и теоретические частоты
(см. табл. 4).
Таблица
4
|
i |
Граница |
Ф(Zi) |
Ф(Zi+1) |
Pi= |
|
|||
|
xi |
xi+1 |
Zi |
Zi+1 |
|||||
|
1 |
120 |
160 |
- |
-1,14 |
-0,5 |
-0,3729 |
0,1271 |
6,36 |
|
2 |
160 |
180 |
-1,14 |
-0,52 |
-0,3729 |
-0,1985 |
0,1744 |
8,72 |
|
3 |
180 |
200 |
-0,52 |
0,11 |
-0,1985 |
0,0438 |
0,2423 |
12,12 |
|
4 |
200 |
220 |
0,11 |
0,73 |
0,0438 |
0,2673 |
0,2235 |
11,18 |
|
5 |
220 |
280 |
0,73 |
+ |
0,2673 |
0,5 |
0,2327 |
11,64 |
4.
Сравним эмпирические и теоретические
частоты. Для этого:
а)
вычислим наблюдаемое значение критерия
Пирсона.
Вычисления
представлены в табл.5.
Таблица
5
|
i |
|
|
|
|
|
|
1 |
5 |
6,36 |
-1,36 |
1,8496 |
0,291 |
|
2 |
10 |
8,72 |
1,28 |
1,6384 |
0,188 |
|
3 |
114 |
12,12 |
1,88 |
3,5344 |
0,292 |
|
4 |
12 |
11,18 |
0,82 |
0,6724 |
0,060 |
|
5 |
9 |
11,64 |
-2,64 |
6,9696 |
0,599 |
|
|
50 |
50 |
|
б) по
таблице критических точек распределения
2
при заданном уровне значимости =0,01
и числе степеней свободы k=m–3=5–3=2
находим критическую точку
;
имеем
.
Сравниваем
c
.
.
Следовательно,
нет оснований отвергать гипотезу о
нормальном законе распределения
изучаемого признака генеральной
совокупности. Т.е. расхождение между
эмпирическими и теоретическими частотами
незначимо (случайно). ◄
Замечание.
Интервалы, содержащие малочисленные
эмпирические частоты (ni<5),
следует объединить, а частоты этих
интервалов сложить. Если производилось
объединение интервалов, то при определении
числа степеней свободы по формуле K=m-3
следует в качестве m
принять число оставшихся после объединения
интервалов.
Пример.
По выборке из 24 вариант выдвинута
гипотеза о нормальном распределении
генеральной совокупности. Используя
критерий Пирсона при уровне значимости
среди заданных значений
= {34, 35, 36, 37, 38} указать: а) наибольшее, для
которого нет оснований отвергать
гипотезу; б) наименьшее, начиная с
которого гипотеза должна быть отвергнута.
Найдем число
степеней свободы
с помощью формулы:
,
где
—
число групп выборки (вариант),
— число параметров распределения.
Так как нормальное
распределение имеет 2 параметра (
и
),
получаем
.
По таблице
критических точек распределения
,
по заданному уровню значимости
и числу степеней свободы
определяем критическую точку
.
В случае а) для
значений
,
равных 34 и 35, нет оснований отвергать
гипотезу о нормальном распределении,
так как
.
А наибольшее среди этих значений
.
В случае б) для
значений 36, 37, 38 гипотезу отвергают, так
как
.
Наименьшее среди них
.◄
2.
Проверка гипотезы о равномерном
распределении.
При использовании критерия Пирсона для
проверки гипотезы о равномерном
распределении генеральной совокупности
с предполагаемой плотностью вероятности
необходимо, вычислив
по имеющейся выборке значение
,
оценить параметры а
и b
по формулам:
, (9)
где а*
и b*
— оценки а
и b.
Действительно, для равномерного
распределения М(Х)
=
,
,
откуда можно получить систему для
определения а*
и b*:

решением которой являются выражения
(9).
Затем, предполагая,
что

можно найти теоретические частоты по
формулам
Здесь s
– число интервалов, на которые разбита
выборка.
Наблюдаемое
значение критерия Пирсона вычисляется
по формуле (7`), а критическое – по таблице
с учетом того, что число степеней свободы
k
= s
– 3. После
этого границы критической области
определяются так же, как и для проверки
гипотезы о нормальном распределении.
3.
Проверка гипотезы о показательном
распределении. В
этом случае, разбив имеющуюся выборку
на равные по длине интервалы, рассмотрим
последовательность вариант
,
равноотстоящих друг от друга (считаем,
что все варианты, попавшие в i
– й интервал, принимают значение,
совпадающее с его серединой), и
соответствующих им частот ni
(число вариант
выборки, попавших в i
– й интервал). Вычислим по этим данным
и примем в качестве оценки параметра λ
величину
.
Тогда теоретические частоты вычисляются
по формуле
Затем сравниваются
наблюдаемое и критическое значение
критерия Пирсона с учетом того, что
число степеней свободы k
= s
– 2.
Пример.
Для выборки, интервальный статистический
ряд которой имеет вид
|
Номер |
Границы |
Эмпирические |
|
1 |
2 |
6 |
|
2 |
5 |
8 |
|
3 |
8 |
15 |
|
4 |
11 |
22 |
|
5 |
14 |
14 |
|
6 |
17 |
5 |
проверить при
уровне значимости α
= 0,05 гипотезу о:
а) показательном;
б) равномерном; в) нормальном законе
распределения генеральной совокупности
с помощью критерия Пирсона.
Объем выборки п
= 70. Будем считать вариантами середины
частичных интервалов: х1
= 3,5, х2
= 6,5,…, х6
= 18,5.
Найдем
= 11,43; σВ
= 4,03; s
= 4,05.
а) Вычислим
теоретические частоты в предположении
о показательном распределении генеральной
совокупности при
аналогично
Наблюдаемое значение критерия
Критическая точка χ2(0,05;4)=9,5;
и гипотеза о показательном распределении
отклоняется.
б) Для равномерного
распределения
теоретические
частоты:
Наблюдаемое значение критерия
Критическая
точка
и гипотеза о равномерном распределении
отклоняется.
в) Теоретические
частоты для нормального распределения:
Так же вычисляются
Наблюдаемое значение критерия
Критическая точка
Поскольку
гипотеза о нормальном распределении
генеральной совокупности принимается.
◄
Критерий
Колмогорова.
Этот критерий
применяется для проверки простой
гипотезы Н0
о том, что независимые одинаково
распределенные случайные величины Х1,
Х2,
…, Хп
имеют заданную непрерывную функцию
распределения F(x).
Найдем функцию
эмпирического распределения Fn(x)
и будем искать границы двусторонней
критической области, определяемой
условием
.
(10)
А.Н.Колмогоров
доказал, что в случае справедливости
гипотезы Н0
распределение статистики Dn
не зависит от функции F(x),
и при
где
—
(11)
— критерий
Колмогорова, значения которого можно
найти в соответствующих таблицах.
Критическое значение критерия λп(α)
вычисляется по заданному уровню
значимости α
как корень уравнения
.
Можно показать,
что приближенное значение вычисляется
по формуле
,
где z
– корень уравнения
На практике для
вычисления значения статистики Dn
используется то, что
,
где
а
— вариационный ряд, построенный по
выборке Х1,
Х2,
…, Хп.
Можно дать следующее геометрическое
истолкование критерия Колмогорова:
если изобразить на плоскости Оху
графики функций Fn(x),
Fn(x)
±λn(α)
(рис. 1), то гипотеза Н0
верна, если график функции F(x)
не выходит за пределы области, лежащей
между графиками функций Fn(x)
-λn(α)
и Fn(x)
+λn(α).