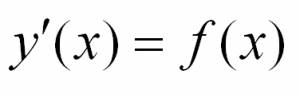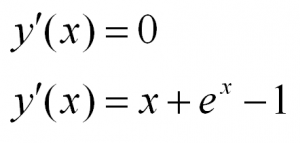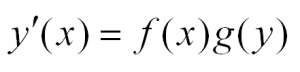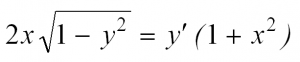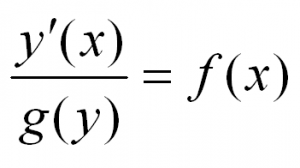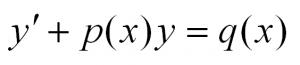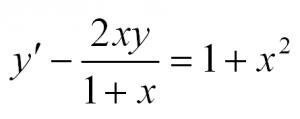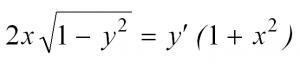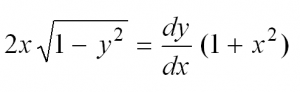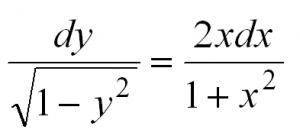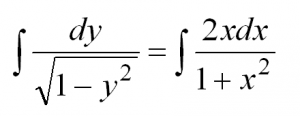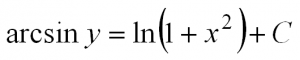Как найти параметр дифференциального уравнения

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Дифференциальные уравнения с малым параметром при производной

Возьмем дифференциальное уравнение (где — параметр)

Если функция в некоторой замкнутой области изменения непрерывна по совокупности аргументов и удовлетворяет условию Липшица по

где не зависит от , то решение (1) непрерывно зависит от .

Во многих задачах физики приходится рассматривать уравнения вида (где — малый параметр)

Разделив обе части уравнения (2) на , приведем его к виду

откуда видно, что правая часть (3) терпит разрыв при , так что теоремой о непрерывной зависимости решений от параметра воспользоваться в этом случае нельзя.

Вопрос ставится так: при каких условиях для малых значений в уравнении (2) можно отбросить член и в качестве приближения к решению дифференциального уравнения (2) рассматривать решение так называемого «вырожденного уравнения»

Пусть для определенности 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> и пусть вырожденное уравнение (4) имеет лишь одно решение . В зависимости от поведения вблизи решения уравнения (4) решение дифференциального уравнения (2) при стремится к решению вырожденного уравнения, либо быстро удаляется от него.

В первом случае решение уравнения (4) называют устойчивым , во втором — неустойчивым .

Именно, если при переходе через график решения вырожденного уравнения (4) функция с возрастанием при фиксированном меняет знак с на , то решение вырожденного уравнения устойчиво и им можно приближенно заменить решение . уравнения (2) (рис. 47).

Если же функция меняет знак с на , то решение вырожденного уравнения (4) неустойчиво и заменять решение дифференциального уравнения (2) решением вырожденного уравнения (4) нельзя (рис. 48).

Достаточные условия устойчивости или неустойчивости выражаются следующими предложениями.

1. Если на решении уравнения (4), то решение вырожденного уравнения устойчиво.

2. Если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAG0AAAAuBAMAAADQGoqnAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAnpQBwUdnMSEQgeDwsdDVhGY9AAAC90lEQVRIx61UTUhUURT+nDs/b6yRcVNCQdIPES66MOgirRnyJ8zISW0RJDObQJzFzNCsgnCMatNiJoso0pqFpERhqAVuGkgTFMyCWoUpSUEbw0atrKRz541vRl5XfdBdvHvfOee755zvnHuA/7Ps0bX/0fWMyx7ExaZ4gZuhtarW9Xwcb3gp9u6PQPVaFTvsl+PMfn6W4rEtLcBaCVgTOTrlhxwXm4G7GDCletBJoW715CoL5biOEArItmAWCDCgLdcffHE58EKvOwW4ncAUpRQ8n8mNM05SrxTW9bnZV4nI18FiNg68TVap5Hf3XySiCoqldM5x++Rr8tMItgi4Jlxpcb7//tg0h9kjw5nIuJ7oPhiHZVHQqoovI7ZngrSVUjoHwCYptDqkcWXfVfFtBEVq+SkZLuiEskA0/FFxDs1wF18Px/r8KBPxLVOqtFd4bKqcDYJOjlmpPy/uOlVfbEmUrwth6lJfyzfRnVJeWGfCPkf7oZ90Pkq4M8fQ9wTsUfiFrRYoT8j82Z6fEDqzCKibwzQSQmSY+KyJTBFbMXndFdEgrEIUOEZdRWwwQT4XJwS4zr60MednZ5t4eXlqVIpTy+KZDmbtL8k+UvbqcRowpL4sTVE6o8P5vNax7F/TgfTWnP5e0cTXMjdYejXRe7DlrD81DWZN0+DS5D3avUWrliNgK/qkXbJyNW3PsLgAVs8NjLpmdfZYjOLQXs1VHAjHGnZvtLTL25/m+DtVuNHScJc+ifYiXJKvErmpOGuELSPcLyPphau1+s0bgDW9W+2XkFU/jFt7ZLAirT9HA7rhf29f4N9zz1KU7YyrLTr1XiijG0asbyk2ycVYM77OZaaY0WV76K+PshvS7patktOtSR6pC38IGYLlDcH8W6k1LfkShnBBP/Ln80KOVMCQP5aMwkHjt9xjkJUVwgzQNDQWJSzUrz6/PR702uJGcArNqZN8y/A0P2KsiDvi17/AvT95Z5uxQDtGxuOwvrlV5TVYdxfH5nrlL0fPxey1y4iJAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> на решении уравнения (4), то решение вырожденного уравнения неустойчиво.

Если вырожденное уравнение (4) имеет несколько решений , то каждое из них должно быть исследовано на устойчивость . При этом поведение интегральных кривых дифференциального уравнения (2) при может быть различным в зависимости от выбора начальных условий — начальной точки .

Возможен также полуустойчивый случай , когда функция при переходе через кривую не меняет знак (например, если есть корень четной кратности вырожденного уравнения (4)). В этом случае при малом интегральные кривые уравнения (2) с одной стороны кривой стремятся к этой кривой, а с другой — удаляются от нее.

В первом случае мы говорили, что начальная точка принадлежит области притяжения полуустойчивого решения , а во втором случае — области отталкивания.

В полуустойчивом случае, как правило, нельзя заменять решение исходного уравнения (2) решением вырожденного уравнения (4).

Можно указать критерии, когда интегральные кривые уравнения (2) при соответствующем выборе начальной точки приближаются к решению вырожденного уравнения и остаются в его окрестности при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, однако это справедливо лишь при отсутствии возмущений уравнения (2).

Приведем эти критерии.

Пусть в окрестности полуустойчивого решения вырожденного уравнения (4) функция . Если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAE4AAAAYBAMAAACmU9bEAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcWdZ4ER4PAxIVGx9LHpLAAAAYVJREFUKM+1kz9LAzEYxp/z2t4fr3CKoEuhWqyrVtBBhKIdughHBSeFji4FERXFpRRxcak6SqEfoTg5iri49cATi/hdfPMmuVYtIoiBJG+SX+7N8yQH/E+x53/HZYrUrIjIq/7E7dCqGYjIyX9bHOuHOaqTVG+Aza/Y3eJJHL9RPaC6D9TanzH3AmU9ZewBiToljSg9S7qOabOLtFaZJBnePbGh5GlnToNWFiNZ4BJYe0qRDDtAshJtwe3JFA++5NLEdYE8zMaxGNc6MKamafFZnasgwQxziQDjVUvMZKhpCWsiLWC5qLkQXpu+6GluQwSzsdJKJ+YsGAE1ilvVXnJJMVfjvDbMNtbFbMtn+wbyFjivTVwdI4GF0XPW1YEbpbIxpzB47J/TKEzMNdmnAEZoEhxKX5RcmuQjXb2/LknfyeeZR/L5Rfrs62OWS2eiO1QPyaB7MKqSH7w3uCUROz09PpXdrj/05dE1q3Iru+3hL1TcsdrB+pyj4ZzTf+cLvK/5l//sA8btRxt561mKAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, то интегральные кривые уравнения (2), приближающиеся к кривой , не могут пересечь эту кривую и остаются в ее окрестности при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> (начальная точка должна находиться в области притяжения полуустойчивого решения ; если находится в области отталкивания, то соответствующая интегральная кривая уравнения (2) быстро удаляется от кривой ) (рис. 49). Если , то интегральные кривые, приближающиеся к графику функции , пересекут его и с другой стороны кривой быстро удалятся от нее. Если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAE4AAAAYBAMAAACmU9bEAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADXRSTlMAQcWdZ4ER4PAxIVGx9LHpLAAAAYVJREFUKM+1kz9LAzEYxp/z2t4fr3CKoEuhWqyrVtBBhKIdughHBSeFji4FERXFpRRxcak6SqEfoTg5iri49cATi/hdfPMmuVYtIoiBJG+SX+7N8yQH/E+x53/HZYrUrIjIq/7E7dCqGYjIyX9bHOuHOaqTVG+Aza/Y3eJJHL9RPaC6D9TanzH3AmU9ZewBiToljSg9S7qOabOLtFaZJBnePbGh5GlnToNWFiNZ4BJYe0qRDDtAshJtwe3JFA++5NLEdYE8zMaxGNc6MKamafFZnasgwQxziQDjVUvMZKhpCWsiLWC5qLkQXpu+6GluQwSzsdJKJ+YsGAE1ilvVXnJJMVfjvDbMNtbFbMtn+wbyFjivTVwdI4GF0XPW1YEbpbIxpzB47J/TKEzMNdmnAEZoEhxKX5RcmuQjXb2/LknfyeeZR/L5Rfrs62OWS2eiO1QPyaB7MKqSH7w3uCUROz09PpXdrj/05dE1q3Iru+3hL1TcsdrB+pyj4ZzTf+cLvK/5l//sA8btRxt561mKAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> при и при t_1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAaiFwGEw00IhQBBx8FF4mUoDAAAAxElEQVQY02NgwANOo/HZHkAZPN/QZNgLoAyhjyAydANcRl4BypAFM1iL4VL9ARB6sb3zAhAtWjwBIhDsrwxhzdCPgDDknCB0R3kHVLuuANQUDqcEEMX4CUhkgxiX4FZzqICkOL4yMBj9Arn+D1yGEyzD/JOBIfEXinc4XBpAlAjQO4wgGaaPzBBXSkBdIK8gLgCWYXFIAguwFkFdnW9gA9HDelkb4tMJsDApMYDIMEyD+A8ROtlQe7AC3DLm3x1waAEFCwDPjC4HC7XnhAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, то при достаточно малом интегральные кривые, выходящие из точки , принадлежащей области притяжения корня , остаются вблизи кривой при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» />; в окрестности точки они пересекают кривую и затем удаляются от нее.

Если в окрестности полуустойчивого решения функция , то для справедливости высказанных утверждений знаки у производной надо заменить противоположными.

Пример 1. Выяснить, стремится ли решение уравнения

удовлетворяющее начальному условию к решению вырожденного уравнения при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> и .

Решение. Имеем , так что решение вырожденного уравнения устойчиво и, следовательно, решение исходного уравнения , выходящее из любой начальной точки , стремится к решению вырожденного уравнения при и t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> (рис.50).

В этом можно убедиться непосредственно проверкой. Решая дифференциальное уравнение (5) как линейное неоднородное при заданном начальном условии , найдем

откуда непосредственно видно, что при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, то есть 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAFQAAAATCAMAAAA56NonAAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEXRSTlMA2FEQQYEhAcCcYYIx8LBwQH4YNZwAAAErSURBVDjLzZTZEoMgDEVZEkgQ0Pz/zxbUcSlo7Uwfmgd0HDjm3oQo9ffhIfr11Yb7rSY+ZEJi1uvmUdzdViv4jOlSyS6kBUba3yYqpj3PnTxYCscLz0Ysj8tgse3HibgxRVOF1hQBWQjhUjuiTtjTD0xwUuhlgZZ8HbAYuDTVghGGfqUckzlg3Q59bClMtoPVYTsMQnOFBM6WGtzDni2lYHSrx9tBmw4UZG9TM+yxQr3W9RGyUsg9zzfowVM1fOrSGZVLrYxu5ONBvk8zVCdfyGVhuLXUZUVYNbWOnntva1AiFfN1pijRUpyhk7zV/txS5aewLuVecbZ3dy/X6/yeKRC16kIax7Qk79yHyeNXT8fd08jdQy4E98VQq9Vn/vWo5NGQ/fkAjtPjrS8ifApdhRxBDgAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> и имеем .

Пример 2. Исследовать на устойчивость решение вырожденного уравнения для уравнения

Решение. Вырожденное уравнение имеет два решения . Имеем

так что решение устойчивое

так что решение вырожденного уравнения неустойчивое (рис. 51).

Пример 3. Исследовать на устойчивость решение вырожденного уравнения, отвечающего уравнению

Решение. Вырожденное уравнение имеет корень второй кратности. Функция 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAALkAAAAaBAMAAAAZC+AvAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAhEGnwQEQMSFh0HHnUV2ErEoAAAL8SURBVEjH1VXPaxNBFH67m83uugSytARFDaF68BSKEfVQi2LSCoJssSeVssWiHkTiLwQPJUr+gAj1UqUYiz0ED1FKD0VCWq3SiFLQoxaSNiYhxL/BN7ObdHc2iSjm4EBmN29mvn3zve+9B/AfjAeRRA/RF7j3vQOX6nKjh74vdUEX8Xeb8WbQvet4+9NfyMQtdAL3RkdAYlf7XNuEVPvjQhan+3HW/NCKsxApwa4NANWwLRKDcyzqbTkB7yo6OHKNsY+tRE24G9pRmMXnnP37yhp7w9V24L4SQL8Ol43vzMI+w2OSu7kB4jryOuxwbp3Zrj5rhz72A70LQSZKv60+bgVpBZQKfQsmQKqi4a3jXIRM/AAdlCp/O/QL+M1xv6xpdNW7GLDsfBH4Onl59FlLqGXgte39JgX9ga94qTfkJpMaHcQ8gYHwnb4XcYTvZjCdgrEXO7qateA5RN8iL7cKA4YQA/lA7RBdmLqbOfYRIMzkdjgEoF0sJE86hBF8nQCubJPtU1O3XAP4beprEcCDZ85bcTwM5yYbJpoD3cAk4GthRyKIQRQGX7ZbDlJ4rmSh8zWkDtEvWedS4jtv3EJXKTF7iXlOBz7OVSWis1dNq5hB/vgSuOAJMxSdq5jo01lrXS6SeZqgczvomyQOHvN+LXRybxf6qB1dKJvM5JpUKKUmzwwzGFqmQPhIeeErbmZ8RSIbIqoYyjZG5L4HiPYiQllEFYTjrqgqZzZTasopdyXrjOqMGVW8lOnkBEpVwQ1RaVD6mcALXc8raMq5FempDoeSjpTz5JMGcGs2Re623oZAoOkXRiHLmE3fIob3JXqWfj5/CvcdYbLJ4wd1/kl61MnMFv4fb9HlXW5mE0ydHaKXz6GwSSWQ4zooiC7psq67K4GCrlwBtlhdBVoJmtViyZZoxCqfoE7OWOWylUJKnq1iHzpV8OXOXYWrf6JVxPz+nR1GXdW8r1N7WO3SEgtU5lb3CPxN9/B3aYmi+fh954NOnU/8F51Z1P/4yC/Sm7UN4zo0AAAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> в окрестности этого корня, и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAG8AAAAYBAMAAAAGzL4qAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/UGBGsE9XKEx4JGxcdABEMZC1QAAAbxJREFUOMvFlM8rBGEYx7+NEbPosWVahexii1ysJU4aLia1sRuR/BFW9kCUNgdpD1OOCsnmIO3FyYl/QPwLUm4aRY7reWfG7OxYW7sXTz3zPu/zvJ+nZ573B/A/0tJeJxg448+xlWK9JnD6EVBehEXPv4Ky5vfMnDoGpTkWCAMJ0LR/2cf2iM/zdXVoOOYB6zjrk4bmvfJVpN77wYjRcOGY56wh1lUTSoe/sIgFSmOu4wFyj5XTlLk3EgPUyRqqDGJn360B1M1jU7Lb4P9qKECaVEdBK3+AFHVIhcGgCeQ2MmILWhegDIYG7H/FTJ+QIS/IZMoaJRtUnGZ8LgCNBQJinAxHcSETZSBIT5kecDlugxx+F0kssEKpQvSUB8zntR8wsl4dJP21BDYapVJjGqqVCn1ZxGRVNBbDjpObQ0kzC0yJ1BWbM2g3B2+Qu4CT+eKumLUVgCXlDrQmZt5y0w4Yzf44tDbe9BY1afVVnJh0TgP1+I5cMhjsFUZm372E17eiGbNb9oJLrt7A7yNHZtHavRtyy0hsCn/RnlPGdvoPeSmBJ1VZYC5sX02t1ldAWbSyvdb+fvTX8XTUId9rEmFOUsSE2wAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Следовательно, решение — полуустойчивое, и если начальная точка лежит в полуплоскости под прямой (область притяжения корня ), то интегральная кривая , выходящая из точки , будет при t_0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAASBAMAAADrvZC0AAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/EGEAcAwIdVhoRCxcVFiSWq88AAAANlJREFUGNNjYMADbqPx2R5AGbxiaDIcDVAGjwiInLkBLuO4AMY4ACL5m+FSihMgtLJhsAKI9mwugAhMDlwMYRUt/ARh+EVBaKUOJaj2gw5QU5iiEkAUixTQeeoghgzcaqajICkmeQaGWTpAl7PJwmXYl4JkmMUZuAXYBZC9wxQKdoprAwNfA4MYyDvMEFc6QV3guMDDOYBFiIGBNSAHLMDZBXV1ooEtcwADUIZT+DRYAuYdBp5WA2awHoYyiP8QoZPNwCnAIoY99Lml2RpwRMwsVQUcMuzaDAwA1XUm63jYJJgAAAAASUVORK5CYII=» style=»vertical-align: middle;» /> оставаться в окрестности линии (рис.52).

Метод введения параметра.

   На практике
при решении уравнений F( x  , y  ,  y ‘ ) = 0 
часто используют следующий метод.

   Предположим ,
что уравнение F( x , y , y ‘ ) = 0 “легко”
решить относительно y :  y = f ( x , y ‘ ). Тогда
введем замену  y ‘  = p  (
параметр зависит от x ). 
Предполагая, что дифференциальное
уравнение имеет решение  y = y ( x )
,   получим ( в силу уравнения 
)

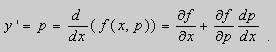
Из этих равенств
выражаем

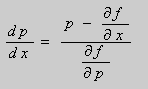
Это уравнение разрешено
относительно производной 
 .
 Пусть его общее решение имеет
вид  p  = p ( x , C ).Тогда
общее решение заданного уравнения
можно записать в виде y =f ( x , p ( x , C ) ).
Решение найдено.     

42. Уравнения n-го порядка с постоянными коэффициентами. Характеристические уравнения. Фундаментальная система решений (фср) однородного уравнения, общее решение неоднородного уравнения.

Уравнение

                       
             (9.1)   называется
линейным дифференциальным уравнением  n-го
порядка с постоянными коэффициентами;  
 —
постоянные вещественные
числа.  Если функция 
)  не
равна тождественно нулю, то иногда
говорят, что  уравнение
с правой частью. 

            Уравнение

                       
                    (9.2) называется
линейным  однородным  дифференциальным
уравнением  n-го
порядка с постоянными коэффициентами;  
 —
постоянные вещественные числа.  Т.
к.  функция 
)  равна
тождественно нулю, то иногда говорят,
что уравнение
без правой части. 

            Уравнение     
                      (9.3) 

называется характеристическим
уравнением, а
его корни – характеристическими
числами  уравнения  (9.2). 

          Система
функций   
  называется линейно
независимой в
интервале  
,
если тождество   (
 —  постоянные
числа)

может
выполняться только когда все 
. Если
к  тому же каждая из функций   
 является
частным решением однородного
уравнения  (9.2), то система
решений одно-родного уравнения
называется  фундаментальной
системой решений.

          Если фундаментальная
система решений найдена, то функция

дает
общее решение однородного
уравнения  (9.2),  ( все 
 —
константы ).   

Неоднородное
уравнение.  Общее
решение неоднородного дифференциального
уравнения с постоянными коэффициентами

можно
найти по формуле   
 (формула
верна и в том случае, когда  коэффици-енты
не являются константами) ,  где  
 —
частное решение неоднородного  уравнения,
а 

    —
общее решение однородного уравнения
.

43. Система линейных дифференциальных уравнений первого порядка. Фср однородной системы. Общее решение однородной и неоднородной системы.

Система
уравнений вида

                                               
,                                                              
(1)

называется неоднородной
системой линейных дифференциальных
уравнений с постоянными коэффициентами.
Будем считать, что 
  являются
непрерывными функциями на (a,b).

Система
дифференциальных уравнений

                                                 
,                                                                     
(2)

называется
однородной.

Определение. Линейнонезависимая
система 
 состоит
из решений однородной системы ЛДУ
называется её фундаментальной системой
решений (ФСР).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных  уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения  определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Приведем пример:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и  взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала  перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все «игреки», а в другой – «иксы»:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»: