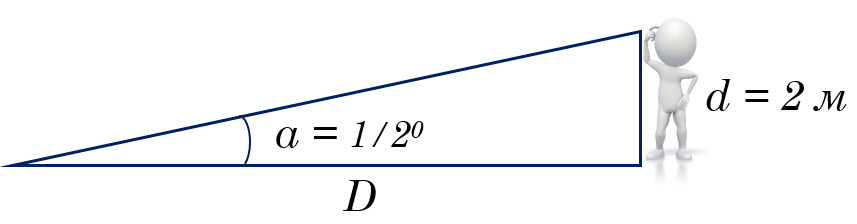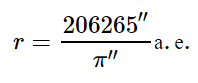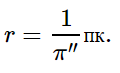Random converter
- Калькуляторы
- Астрономия
Калькулятор расстояния и годичного параллакса
Калькулятор определяет расстояние до недалекой звезды в световых годах и парсеках, если известен годичный параллакс этой звезды в угловых секундах. Можно также определить параллакс, если известно расстояние.
Пример: рассчитать расстояние в световых годах до самой яркой звезды звездного неба северного полушария Арктура (α Волопаса) в созвездии Волопаса, если известно что ее параллакс равен 88.83 угловым миллисекундам.
Параллакс
p
Расстояние
D
Поделиться ссылкой на этот калькулятор, включая входные параметры
Определение параллакса и формула для расчета расстояния
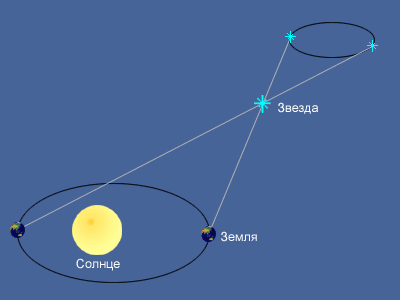
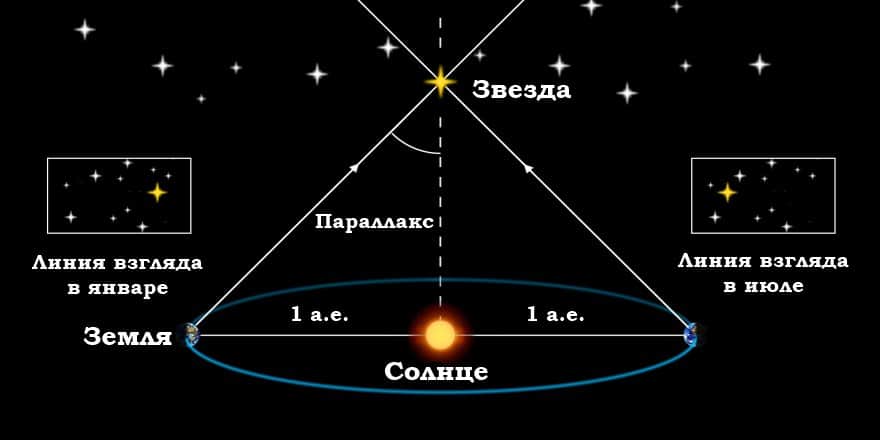
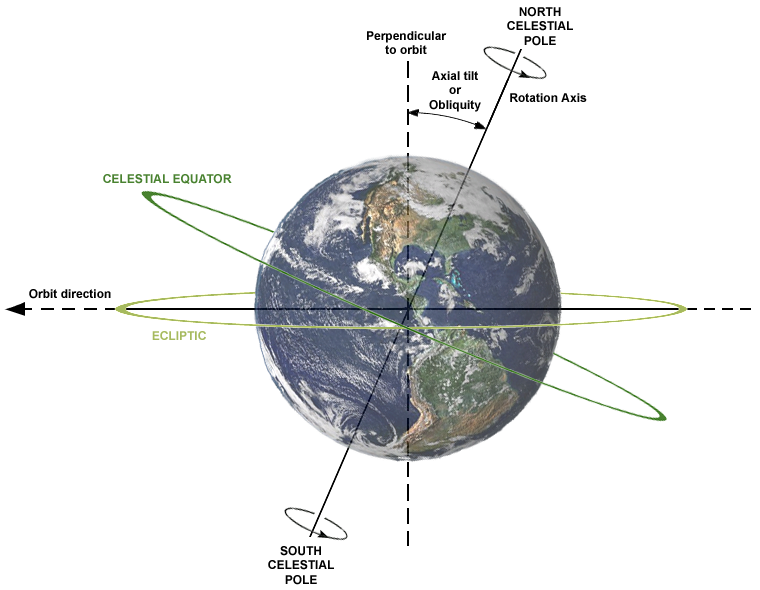
Параллакс — это изменение видимого кажущегося положения объекта, наблюдаемого с разных точек и измеренное как угол (или половинный угол) между направлениями от наблюдателя на объект. Годичный звездный параллакс — это изменение положения звезды, наблюдаемой с двух находящихся на большом расстоянии друг от друга точек. Эти две точки наблюдения расположены на земной орбите, как показано ниже. Параллакс небесного тела можно использовать для нахождения расстояния до него по формуле:
Здесь D — расстояние до небесного тела, измеренное в парсеках, и p — наблюдаемый годичный параллакс, измеренный в дуговых секундах. Эта формула и используется для расчетов в нашем калькуляторе. Парсек определяется как расстояние до объекта, годичный звездный параллакс которого равен 1 дуговой секунде. Иными словами, парсек — это расстояние, с которого диск размером в 1 а.е. будет иметь угловой размер в 1 угловую секунду.
Годичный параллакс звезды (чертеж не в масштабе); 1 — астрономическая единица (а.е.), то есть расстояние от Земли до Солнца; D — расстояние от центра земной орбиты до звезды S; p — параллакс, измеренный в угловых секундах («)
Подробнее о длине и расстоянии: измерение расстояний в космосе
Общие сведения
Космос огромен — поэтому космические расстояния измеряются не так, как это делается на Земле. В статье о длине и расстояниях мы говорили главным образом об измерении относительно небольших расстояний, которые не трудно себе представить. Однако расстояния в космосе представить себе очень трудно из-за их огромной величины, а привычные метры и километры едва ли годятся для использования в космосе. Для измерения расстояний между планетами и галактиками вряд ли можно использовать измерительные приборы типа рулетки или линейки. Спутниковая навигация в космосе тоже не работает. Поэтому для космоса придется ввести не только новые единицы измерения, но и новые методы измерения этих расстояний.
Измерения с помощью радиолокации
Расположенная на Земле радиолокационная станция (РЛС) посылает СВЧ-излучение в сторону астрономического объекта, расстояние до которого нужно вычислить. Затем измеряется время, которое необходимо, чтобы сигнал достиг объекта и вернулся назад, к РЛС. Зная это время и скорость света в вакууме, можно определить расстояние, умножая скорость на время.
Использовать РЛС для этих измерений удобно не только для определения расстояния до нужного астрономического объекта, но и для оценки скорости изменения этого расстояния (ведь объекты во Вселенной движутся друг относительно друга!). Это, в свою очередь, полезно при слежении за перемещениями объектов в космосе, например, для оценки возможности столкновения астероида с Землей.
Этот метод ограничен астрономическими объектами, которые находятся на небольших расстояниях от Земли. Можно сказать, что он пригоден для объектов, находящихся в пределах Солнечной системы. Это связано с тем, что радиосигнал ослабляется и рассеивается на больших расстояниях. Кроме того, чем больше расстояние, тем больше должен быть объект для того, чтобы его могла «увидеть» радиолокационная станция.
Годичный звездный параллакс
В статье о длине и расстоянии мы уже обсуждали годичный звездный параллакс. Здесь мы кратко рассмотрим это явление, потому что именно параллакс используется для измерения расстояний в космосе. Параллакс — геометрические явление, используемое для определения расстояний. Он хорошо выражен, если наблюдать объект с разных точек зрения относительно удаленного фона. Познать суть параллакса достаточно легко: вытяните перед собой палец или карандаш и закройте один глаз. Отметьте насколько далеко этот палец от другого объекта (скажем, от дерева, если вы на улице, или от шкафа, если вы находитесь в помещении). Теперь закройте этот глаз и откройте другой. Заметили, что палец или карандаш переместился относительно удаленного объекта? Это перемещение и является параллаксом. Если проделать аналогичный эксперимент, удерживая палец ближе к глазам, можно заметить, что расстояние, на которое перемещается палец или карандаш относительно удаленного объекта, стало больше. Чем ближе палец к глазам, тем больше он сдвигается относительно удаленного объекта при рассматривании пальца обоими глазами. Понятно, что это явление можно использовать для измерения расстояния до объекта, в данном случае — пальца.
На этом рисунке два положения Земли обозначены голубыми кружками, а Солнце — оранжевое. А — реальное положение звезды, расстояние до которой необходимо измерить. А2 и А3 — кажущиеся положения этой звезды с двух точек наблюдения относительно удаленной белой звезды DS. Р — параллактический угол. Измеряемое расстояние между Солнцем и звездой, обозначенное оранжевой линией AS, равно одному парсеку, если угол Р равен одной дуговой секунде.
Более подробное математическое объяснение измерения расстояний с помощью параллакса приводится в статье о длине и расстоянии. В общем случае, можно сказать, что расстояния следует измерять, когда Земля находится в двух противоположных точках ее орбиты вокруг Солнца (с интервалом в шесть месяцев, так как Земля делает один оборот вокруг Солнца за один год). Мы используем известное расстояние от Земли до Солнца (точно измеренное и называемое астрономической единицей) и измерим угол, образованный линией, соединяющей Землю в точке первого измерения, звезду, расстояние до которой измеряется, и точкой, в которой находится Земля во время второго измерения. Фактически, нам нужно знать только половину этого угла, которая называется параллактическим углом и обозначена на рисунке буквой P. Таким образом, имеется достаточно информации, чтобы рассчитать расстояние от Земли до звезды с помощью тригонометрических уравнений.
С помощью описанного метода можно измерить расстояние в различных единицах длины, но астрономы предпочитают парсек. Один парсек — это расстояние от Солнца до рассматриваемой звезды, если параллактический угол равен 1 дуговой секунде. Другой единицей длины является световой год (1 парсек = 3,26 светового года), однако эту единицу чаще используют журналисты. Астрономы предпочитают парсеки.
Четыре звезды имеют один и тот же размер, но расположены на разных расстояниях от нас. Звезда в положении 1 находится ближе всего, а звезда в положении 4 на максимальном удалении от нас. В результате мы видим ближние к нам звезды как более яркие, а удаленные — как менее яркие. Если известная их реальная яркость, можно сравнить ее с их кажущейся яркостью и, таким образом, узнать расстояние до них
Как и при радиолокационных измерениях, этот метод ограничен расстоянием, на которое удалена звезда. Если она слишком далеко (более 500 парсеков), то угол, который нужно измерить, слишком мал и измерить его практически невозможно. Поэтому для больших расстояний данный метод не работает.
Цефеиды
Для измерения расстояний в космосе можно использовать определенные типы звезд, называемых Цефеидами. Цефеида — пульсирующая звезда с точной зависимостью светимости (яркости) от периода пульсации. Чем больше этот период, тем выше яркость Цефеид. Эта корреляция между периодом пульсации я светимостью хорошо известна и все Цефеиды ведут себя одинаково. Поэтому, если известен период пульсации, который несложно наблюдать, можно измерить светимость звезды. Мы знаем, что чем дальше звезда, тем меньше ее яркость. Таким образом, если сравнить реальную яркость с кажущейся, можно определить расстояние до звезды.
Пульсация цефеид обусловлена их сжатием и расширением. При этом их яркость изменяется, и для определения периода нужно измерить время между точками с максимальной яркостью. Ядро звезды не изменяет размеры, однако их внешние газовые слои расширяются и сжимаются вследствие флуктуаций давления газа в этих слоях. Сжатие и расширение происходит за счет двух сил: гравитационного притяжения, которое приводит к сближению молекул газа в направлении центра звезды, и давления газа, которое приводит к расширению внешнего слоя.
Схематическое изображение пульсирующей Цефеиды с периодом в два дня. Пики светимости 1 декабря 2010 г., когда звезда начинает постепенно терять яркость. 2 декабря яркость минимальная. Затем звезда снова достигает максимальной светимости 3 декабря и уменьшает светимость 4 декабря и так далее
Когда звезда находится в сжатом состоянии, ее фотоны имеют высокую энергию и в результате давление повышается, что приводит к расширению внешней оболочки звезды. Когда это давление падает и становится меньше гравитационных сил, сжимающих оболочку, звезда сжимается. Затем процесс повторяется.
Цефеиды можно использовать для измерения расстояний до 40 миллионов парсеков, то есть намного больших, чем позволяет метод параллакса. Недостаток метода — цефеиды не так уж часто встречаются.
Сверхновая типа Ia
Еще одним стандартным измерителем расстояния являются сверхновые типа Ia. Идея аналогичная использованию Цефеид: при известной реальной светимости сверхновой в момент взрыва, когда яркость максимальна, можно сравнить ее с видимой яркостью звезды и, таким образом, определить насколько далеко она от нас. Именно эта категория сверхновых интересует нас в связи с тем, что они наиболее хорошо изучены, а их поведение предсказуемо, поэтому максимальная светимость во время взрыва хорошо известна. Эти взрывы происходит с двумя астрономическими объектами — с белыми карликами и еще одним белым карликом или со звездой-гигантом. Белый карлик представляет собой звезду очень высокой плотности в конце ее жизненного цикла, когда эта звезда «всасывает» материю находящихся рядом звезд (в нашем случае — второй звезды) до тех пор, пока не взорвется. Эти взрывы сверхновых позволяет измерять расстояния до галактик, в которых они находятся.
Другие методы измерения расстояний
Имеется еще несколько методов измерения расстояний в космосе. Один из них основан на предположении, что вселенная расширяется с известной скоростью. Если известна скорость, с которой галактики удаляются от нашей галактики, то с помощью закона Хаббла можно рассчитать насколько далеко они от нас. Закон Хаббла гласит, что расстояние до галактики равно скорости галактики, деленной на постоянную Хаббла, которая является известной константой. Скорость галактики можно определить, изучая спектр галактики, а затем, учитывая эффект Доплера, можно определить расстояние. Эффект Доплера, более известный в астрономии как смещение Доплера — это изменение частоты электромагнитного излучения (в нашем случае — света), излучаемого объектом, который движется относительно наблюдателя. При движении в сторону от наблюдателя этот спектр сдвигается в сторону низких частот, то есть в красную сторону, причем степень сдвига зависит от скорости удаления галактики. По смещению можно рассчитать скорость, а затем вычислить расстояние.
Примеры расчета расстояния до некоторых звезд и их звездного параллакса
Параллакс в дуговых миллисекундах и расстояние в световых годах
Канопус (α Киля)
Ригель Кентаурус (α Центавра A)
Сириус (α Большого Пса)
Вега (α Лиры)
Капелла (α Возничего)
Ригель (β Ориона)
Альтаир (α Орла)
Альдебаран (α Тельца)
Антарес (α Скорпиона)
Арктур (α Волопаса)
Unit Converter articles were edited and illustrated by Анатолий Золотков
Почему так трудно определить размеры небесных объектов и расстояния до них? Все дело в том, что размеры удаленных объектов мы можем определить только по сравнению размерами известных объектов, а на небе нам не с чем сравнивать. Мы видим на небе множество светящихся точек, но яркость точки может определяться как ее размером, абсолютной светимостью, так и расстоянием до нее.
Поэтому в астрономии практически невозможно определить оптическими методами линейный размер удаленного объекта, можно определить только его угловой размер.
Древние греки изобрели тригонометрию, которая позволяет определить количественные соотношения между углами, линейными размерами и линейными расстояниями. С помощью простых математических соотношений, включающих базовую тригонометрию, мы можем вычислить расстояния до удаленных объектов, размеры которых известны (или размеры, если расстояния известны).
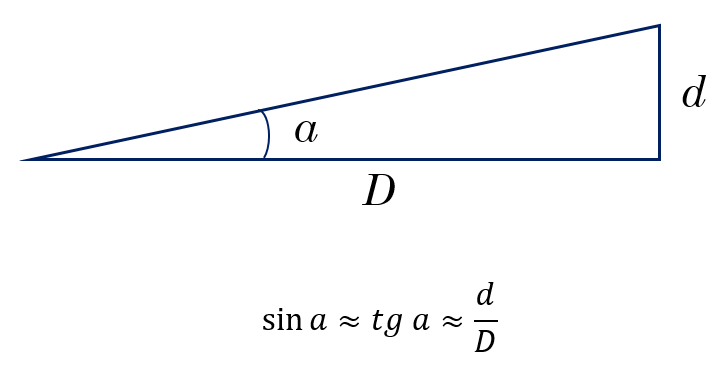
Уравнение малых углов
Если углы малые, то синус угла примерно равен тангенсу, который, в свою очередь примерно равен самому углу в радианной мере.
Уравнение малых углов включает в себя угловой размер объекта, его линейный размер и расстояние. Если известны какие-либо две из этих величин, можно вычислить третью. Обратимся к угловому размеру с символом a, выраженному в секундах дуги. Обозначим диаметр объекта как d, а расстояние до него как D. Тогда уравнение малого угла
a / 206 265 = d / D
Число 206 265 называется константой пропорциональности. Число 206 265 на самом деле является числом секунд дуги в угле 57,3°, который является специальным углом, называемым радианом. Радиан определяется как центральный угол дуги, длина которой равна радиусу окружности. Длина окружности равна 2πr, Радиан равен 360° / 2 π = 57,3° или около шестой части полного круга.
Вот пример использования уравнения малого угла. Предположим, что ваш друг ростом в 2 метра стоит через поле от вас, где он виден под углом ½°, или 1800″. Как он далеко от вас? Мы хотим найти расстояние D, выразим эту величину из уранения:
D = 206 265 d / a
Используя метрические единицы, найдем
D = (2.1 x 105 x 2) / (1.8 x 103) = 2.3 х 102 метра = 230 метров
Если ваш друг имеет рост 2 метра и угловой размер его составляет ½ ° (или 1800 угловых секунд), расстояние D составляет 230 метров. Обратите внимание, что мы округляем все наши оценки до двух значащих цифр, потому что измерение угла вряд ли будет очень точным.
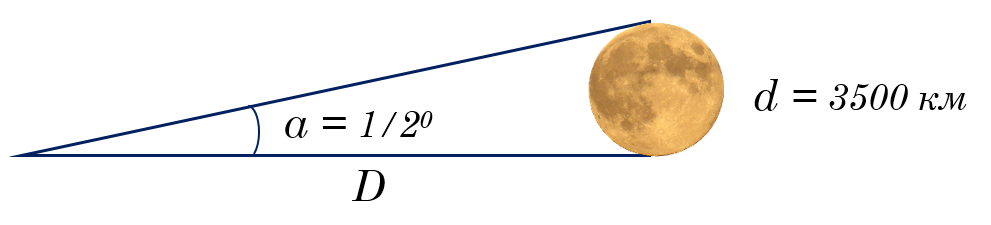
Как поняли древние греки, уравнение малого угла можно использовать для определения астрономических расстояний. Они не могли точно измерить диаметр Луны, но они знали ее угловой размер a, который также составляет примерно ½°, или 1800″.
Если мы используем современные знания о том, что диаметр Луны составляет около 3500 километров, мы можем оценить расстояние до нее так же, как мы это сделали для расстояния друга выше. В метрических единицах d будет 3,5 × 106 метров. Уравнение будет гласить:
D = (2.1 × 105 × 3.5 × 106) / (1.8 × 103) ≈ 4 х 108 метров ≈ 4 x 105 километров.
Реальное среднее расстояние до Луны 384 000 км. Неплохая точность!
Методы определения расстояний до звезд
Годичный параллакс
Кажущееся перемещение более близкой звезды на фоне очень далеких звезд происходит по эллипсу с периодом в 1 год и отражает движение наблюдателя вместе с Землей вокруг Солнца. Маленький эллипс, описываемый звездой, называется параллактическим эллипсом. В угловой мере большая полуось этого эллипса равна величине угла, под которым со звезды видна большая полуось земной орбиты, перпендикулярная направлению на звезду. Этот угол называется годичным параллаксом (π).
Параллактические смещения звезд служат неопровержимым доказательством обращения Земли вокруг Солнца. Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите.
Если CT = a есть средний радиус земной орбиты, SC = r — расстояние до звезды S от Солнца C, а угол π — годичный параллакс звезды, то
Так как годичные параллаксы звезд оцениваются десятичными долями секунды, а 1 радиан равен 206265′′, то расстояние до звезды можно определить из соотношения
При измерении расстояний до звезд астрономическая единица слишком мала. Поэтому для удобства определения расстояний до звезд в астрономии применяется специальная единица длины — парсек (пк), название которой происходит от слов «параллакс» и «секунда».
Парсек — это расстояние, с которого радиус земной орбиты был бы виден под углом в 1′′.
1 пк = 206 265 а. е. = 3,086 · 1013 км.
Таким образом, расстояние до звезд в парсеках будет определяться выражением
В астрономических единицах обычно выражаются расстояния до тел Солнечной системы. Расстояния до небесных тел, находящихся за пределами Солнечной системы, обычно выражаются в парсеках, килопарсеках (1 кпк = 103 пк) и мегапарсеках (1 Мпк = 106 пк), а также в световых годах (1 св. г. = 9,46 · 1012 км = 63 240 а. е. = 0,3067 пк или 1 пк = 3,26 св. г.).
Световой год — расстояние, которое электромагнитное излучение (в вакууме) проходит за 1 год.
Источник
Фотометрический метод определения расстояний
Освещенности, создаваемые одинаковыми по мощности источниками света, обратно пропорциональны квадратам расстояний до них. Следовательно, видимый блеск одинаковых светил (т.е. освещенность, создаваемая у Земли на единичной площадке, перпендикулярной лучам света) может служить мерой расстояний до них. Выражение освещенностей в звездных величинах (m — видимая, M — абсолютная звездная величина) приводит к следующей основной формуле фотометрических расстояний rф(пк):
Для светил, у которых известны тригонометрические параллаксы, можно, определив M по этой же формуле, сопоставить физические свойства с абсолютными звездными величинами. Это сопоставление показало, что абсолютные звездные величины многих классов светил (звезд, галактик и др.) можно оценивать по ряду их физических свойств.
Основным способом оценки абсолютных величин звезд является спектральный способ: в спектрах звезд одного и того же спектрального класса обнаружены особенности, указывающие на их абсолютные величины (чаще всего это усиление линий ионизованных атомов с возрастанием светимости звезд). По таким признакам звезды разделены на классы светимости. По классам и более мелким подклассам светимости, оцениваемым по спектрам звезд, можно находить абсолютные величины с погрешность до 0,5m. Эта погрешность соответствует относительной погрешности 30%.
Цефеиды (стандартные свечи)
Важный метод определения фотометрических расстояний в Галактике и до соседних звездных систем — галактик — основан на характерном свойстве переменных звезд — цефеид. Короткопериодические цефеиды (с периодами колебаний блеска менее суток) в среднем имеют абсолютную величину +0,5m. Они встречаются в шаровых звездных скоплениях, в центральной области и сферической короне Галактики и относятся к ее звездному населению II типа. По цефеидам в конечном счете найдены расстояния до шаровых звездных скоплений и установлено расстояние от Солнца до центра Галактики.
Для долгопериодических цефеид (периоды колебаний от 1 до 146 сут.), относящихся к звездному населению I типа (плоской составляющей Галактики), установлена важная зависимость период-светимость, согласно которой, чем короче период колебаний блеска, тем цефеида слабее по абсолютной величине. С помощью этой зависимости можно определить абсолютные величины цефеид по длительности их периодов колебаний блеска и, следовательно, фотометрические расстояния до цефеид и звездных скоплений, спиральных рукавов и звездных систем, где они наблюдаются (см. Период-светимость зависимость). Погрешность определения расстояний по цефеидам составляет для звездных скоплений в среднем 40% (в отдельных случаях меньше).

- Информация о материале
-
Просмотров: 15633
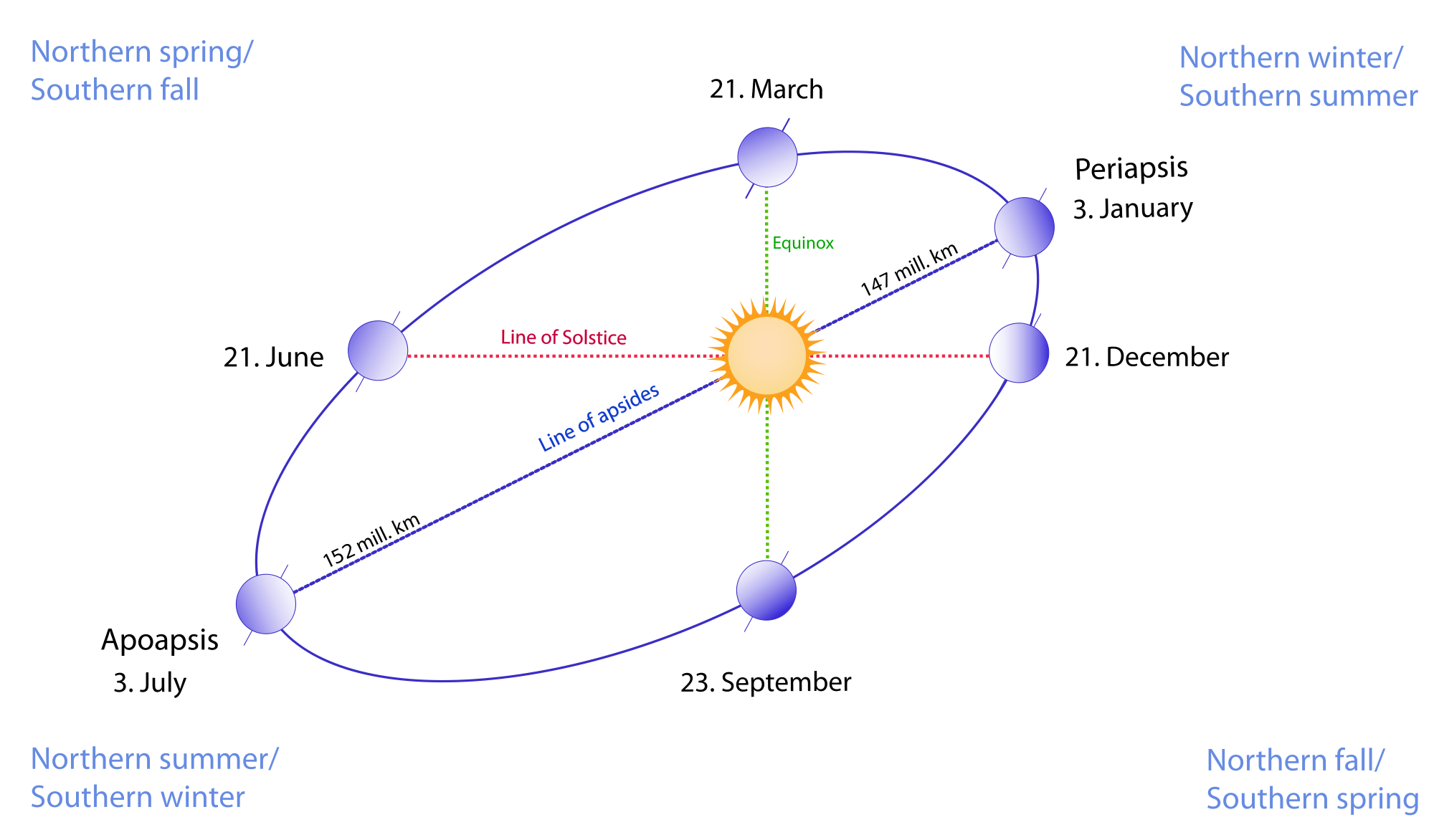
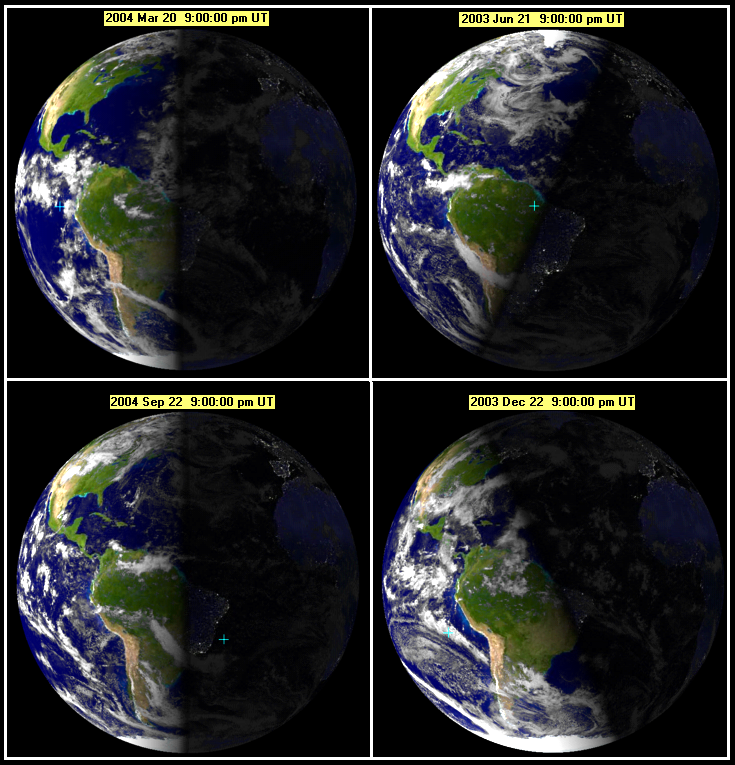
Смена времен года — вечное и неизменное явление природы. Причина его заключается в движении Земли вокруг Солнца.
Путь, по которому в космическом пространстве движется земной шар, имеет форму вытянутого круга — эллипса. Солнце находится не в центре этого эллипса, а в одном из его фокусов. Поэтому на протяжении года расстояние от Солнца до Земли периодически меняется: от 147,1 млн. км (в начале января) до 152,1 млн. км (в начале июля). Переход от тёплого времени года (весна, лето) к холодному (осень, зима) происходит вовсе не потому, что Земля то приближается к Солнцу, то удаляется от него.
Истинная причина смены времен года — это наклон земной оси. Ось вращения, воображаемая линия, соединяющая северный и южный полюса Земли, не перпендикулярна плоскости земной орбиты, по которой она движется вокруг Солнца. И отклонение оси от перпендикуляра составляет 23,5°. Ось направлена на север в точку среди звезд возле Полярной звезды. (На самом деле, ось медленно меняет свое направление и со временем будет указывать не на Полярную, а на другую звезду.)
Лето приходит в Северное полушарие, когда ось, направленная через Северный полюс вверх, указывает примерно в сторону Солнца. В этой ситуации Солнце в полдень находится выше над горизонтом, чем во все остальные сезоны года, поэтому оно лучше освещает Северное полушарие и дает больше тепла. В это же самое время ось, проходящая вниз через Южный полюс, направлена от Солнца, поэтому Солнце в полдень находится ниже над горизонтом, чем в любое другое время года, и хуже освещает Южное полушарие. В это время в Австралии наступает зима.
Летом светлого времени суток больше, чем зимой, потому что Солнце находится выше над горизонтом. Поэтому ему требуется больше времени, чтобы сначала подняться на эту высоту, а потом — спуститься. И, поскольку день длится дольше, в это время года теплее.
По мере того как Земля движется по орбите вокруг Солнца, кажется, что Солнце перемещается по небу по некой окружности, которая называется эклиптикой. Плоскость эклиптики наклонена к плоскости экватора точно под таким же углом, как ось Земли — 23,5°.
Равноденствие — момент пересечения небесного экватора центром видимого солнечного диска. Весеннее равноденствие наступает, когда Солнце переходит из южного полушария небесной сферы в северное и обычно происходит около 21 марта. Осеннее равноденствие бывает около 23 сентября. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце переходит из южного полушария небесной сферы в северное, т. е. пересекает небесный экватор «снизу вверх», наступает первый день весны, который называется днем весеннего равноденствия. Он приходится на 20–21 марта. В Южном полушарии Земли наступает астрономическая осень, а в Северном — астрономическая весна. Вблизи равноденствия продолжительность дня в средних широтах примерно равна продолжительности ночи.
Когда Солнце достигает самой высокой (северной) точки на эклиптике, это день летнего солнцестояния. Приходится примерно на 21–22 июня. С этого дня в Северном полушарии начинается астрономическое лето, а в Южном — астрономическая зима.
Когда Солнце переходит из северного полушария небесной сферы в южное, т. е. пересекает небесный экватор «сверху вниз», это начало осени, день осеннего равноденствия. Обычно он приходится примерно на 23 сентября. В Южном полушарии Земли наступает астрономическая весна, а в Северном — астрономическая осень.
Когда Солнце достигает самой нижней (южной) точки на эклиптике, это день зимнего солнцестояния. Приходится примерно на 21–22 декабря. С этого дня в Северном полушарии начинается астрономическая зима, а в Южном — астрономическое лето.
Источник

- Информация о материале
-
Просмотров: 8856
ПРАКТИЧЕСКАЯ РАБОТА
ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ ДО ЗВЕЗД
МЕТОДОМ ГОДИЧНОГО ПАРАЛЛАКСА
Цели занятия:
1. Научится определять расстояния до звёзд с
помощью годичного параллакса.
2. Развить логического мышления, развитие умения
решать задачи.
3. Формировать научное мировоззрение и
диалектическое мышление.
Ключевые слова: звезды, годовой параллакс, астрономическая
единица, парсек.
Теоретический материал
Астрономические единицы.
Поскольку расстояние между астрономическими объектами
(планетами, звёздами, галактиками), огромны, пользоваться обычными единицами
длины – метры и километры – неудобно. Поэтому в астрономии приняты особые
единицы измерения расстояний: астрономическая единица, парсек и световой год.
Астрономическая единица (а.е.) равна среднему расстоянию от Земли до Солнца (149 600 000 км)
Парсек — расстояние, из которого а.е. (средний радиус орбиты
Земли) видна под углом 1» (секунда дуги): 1 пк = 206 265 а.е.
= 30 857 244 000 000 км = 3,08 ×
1013 км.
Световой год –
это расстояние, которое преодолеет световой поток за время, равное
календарному году:
1 св.год = 3 × 105 км/с × 365,25дней × 24часов × 3600 сек. = 9 467 280 000 000
км = 9,46 × 1012 км.
1 пс = 3,26 св.лет.
Годичный параллакс
Как измерить расстояние, если
до предмета не дотянуться ни линейкой, ни лучом локатора? На помощь приходит
метод триангуляции, широко применяемый в обычной земной геодезии.

длины – «базу»( на рисунке – точки А и С), измеряем из его концов углы, под
которыми видна недоступная по тем или иным причинам точка В, а затем простые
тригонометрические формулы дают искомое расстояние.
Когда мы переходим с одного
конца базы на другой, видимое направление на точку меняется, она сдвигается на
фоне далёких объектов. Это называется параллактическим смещением, или параллаксом.
Величина параллакса тем
меньше, чем дальше объект, и тем больше, чем длиннее база.
Для измерения
расстояний до звёзд приходится брать максимально доступную астрономам базу,
равную диаметру земной орбиты. Соответствующее параллактическое смещение звёзд
на небе (строго говоря, его половину) стали называть годичным параллаксом.

называется угол, под которым со звезды можно было бы видеть большую полуось
земной орбиты (равную 1 а. е.), перпендикулярную направлению на звезду.
Определить расстояние до
звезды можно, зная годовой параллакс ρ– угол, под которым со звезды был виден
радиус земной орбиты. Для этого звезду фотографируют с помощью телескопа через
каждые 6 месяцев, то есть из двух противоположных точек земной орбиты. На
фотографиях близкая звезда несколько меняет своё положение относительно других,
более удалённых. Если это смещение таково, что его можно измерить, то вычислив
соответствующий угол, можно рассчитать расстояние до звезды по формуле
где а — средний радиус земной
орбиты , D — расстояние до звезды ,
ρ — её годичный параллакс.
Если углы малые, то синус малого угла можно заменить
величиной самого угла в радианной мере:
sin p ≈ p’’/206265. Тогда получаем: D = a∙206265/p’’, или
в астрономических единицах.
Если расстояние нужно выразить в парсеках (1 пк = 206265
а.е.), то
Примеры решения
Задача №1:
Годичный
параллакс самой близкой к нам звезды Проксима из созвездия Кентавра — 0,762″.
Каково до неё расстояние (в пк, св.годах, км).
Дано: ρ = 0,762″ Решение: Dпс = 1 / ρ = 1 / 0,762 пк = 1,31 пк ,
Dпс — ? Dсвг = 3,26 св.лет × 1,31 = 4,27 св.лет ,
Dсв.г — ? Dr =
4,27 × 9,46 × 1012 км = 40,39 × 1012 км,
D — ? или D = 1,31 × 3,08 × 1013 км = 40,39 × 1012 км.
Задача
№2:
Найти расстояние до звезды Альдебаран (α созвездия Телец) , имеющей
годичный параллакс 0,05″. Выразите это расстояние в парсеках, световых годах и
километрах.
Дано: ρ = 0,05″ Решение: D пс = 1 / ρ =
1 / 0,05 пк = 20пк ,
D пс — ? D свг. = 3,26 св.лет × 20 = 65,2 св.лет ,
Dсв.г — ? D =
65,2 × 9,46 × 1012 км = 616,792 × 1012 км.
D — ?
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ
Задача №1. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Арктура (α в
созвездии Волопаса) если известно, что её параллакс равен 88.83 угловым
миллисекундам.
Задача №2. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Канопус (α в
созвездии Киля) если известно, что её параллакс равен 10.55 угловым
миллисекундам.
Задача №3. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Ригель
Кентаурус (α в созвездии Центавра A) если известно, что её параллакс равен
754,81 угловым миллисекундам
Задача №4. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Сириус (α в
созвездии Большого Пса) если известно, что её параллакс равен 379,21 угловым
миллисекундам
Задача №5. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Вега (α в
созвездии Лиры) если известно, что её параллакс равен 130,23 угловым миллисекундам
Задача №6. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Капелла (α в
созвездии Возничего) если известно, что её параллакс равен 76,2 угловым
миллисекундам
Задача №7. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Ригель (β в
созвездии Ориона) если известно, что её параллакс равен 3,78 угловым
миллисекундам.
Задача №8. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Альтаир (α в созвездии Орла) если известно, что её параллакс
равен 194,95 угловым миллисекундам.
Задача №9. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Антарес (α в
созвездии Скорпиона) если известно, что её параллакс равен 5,89 угловым
миллисекундам
Задача №10. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Альдебаран
(α в созвездии Тельца) если известно, что её параллакс равен 49,97 угловым
миллисекундам.
Задача №11. Рассчитать расстояние в
световых годах до яркой звезды звёздного неба северного полушария Денеб (α в
созвездии Лебедь) если известно, что её параллакс равен 0,003 угловым
миллисекундам
Литература.
Астрономия.
Учебник для 10 класса средней школы. (Издание 15-ое). Издательство: Москва
«Просвещение» Год: 1983., 145 страниц.
Калькулятор
параллакса и расстояний онлайн _
https://www.translatorscafe.com/unit-converter/ru-RU/calculator/parallax-distance/
Ответы
|
1 |
11,257 |
36,72 СГ |
3,47*1014 |
|
2 |
94,787 |
309,15 СГ |
2,92*1015 |
|
3 |
1,325 |
4,32 СГ |
4,09*1013 |
|
4 |
2,637 |
8,6 СГ |
8,14*1013 |
|
5 |
7,679 |
25,04 СГ |
2,37*1014 |
|
6 |
13,123 |
42,8 СГ |
4,05*1014 |
|
7 |
264,55 |
862,85 СГ |
8,16*1015 |
|
8 |
5,13 парс |
16,73 СГ |
1,58*1014 |
|
9 |
169,779 |
553,75 СГ |
5,24*1015 |
|
10 |
20,012 |
65,27 СГ |
6,18*1014 |
|
11 |
333,333 |
1087,19 |
1,03*1016 |
Светило науки — 1509 ответов — 6948 раз оказано помощи
Ответ: 1) Параллакс звезды ≈ 0,01619»
2) Радиус звезды ≈ 52,5 радиусов Солнца
Объяснение: 1) Параллакс звезды, расположенной на расстоянии 206265 астрономических единиц (что равно 1 парсеку) = 1 секунде. Следовательно, параллакс звезды, расположенной на заданном расстоянии р» = 206265/12740000 = 0,01619»
2) Дано:
Светимость Солнца Lс = 1
Температура Солнца 5780 К
Радиус Солнца Rс = 1
Светимость звезды Lз = 200
Температура звезды Тз = 3000 К
Найти радиус звезды Rз — ?
Светимость звезды пропорциональна четвертой степени температуры (Т) звезды и зависит от площади её поверхности, которая пропорциональна квадрату радиуса (R) звезды.
Таким образом, отношение светимостей Солнца и звезды:
Lз/Lс = (Rз/Rс)²(Тз/Тс)^4. Так как Lс и Rс приняты за 1, то последнее выражение принимает вид: Lз = (Rз)²(Тз/Тс)^4. Отсюда Rз² = Lз(Тс/Тз)^4. Следовательно, Rз = √{Lз(Тс/Тз)^4}.
Подставив числовые значения параметров, имеем:
Rз = √{200(5780/3000)^4} ≈ 52,5 радиусов Солнца
Наше Солнце справедливо называют типичной звездой. Но среди
большого и разнообразного числа звёзд есть немало таких, которые значительно
отличаются от него по своим физическим характеристикам и химическому составу.
Поэтому полное представление о звёздах даст такое определение:
Звезда — это массивный газовый шар, излучающий свет и
удерживаемый в состоянии равновесия силами собственной гравитации и внутренним
давлением, в недрах которого происходят (или происходили ранее) реакции
термоядерного синтеза.
Мысли о том, что звёзды — это далёкие солнца, высказывались
ещё в глубокой древности. Но из-за колоссальных расстояний до них диски звёзд
не видны даже в самые мощные телескопы. Поэтому, чтобы найти возможность
сравнивать звёзды между собой и с Солнцем, необходимо было придумать способы
определения расстояний до них.
Ещё Аристотель предполагал, что если Земля движется вокруг
Солнца, то, наблюдая за звездой из двух диаметрально противоположных точек
земной орбиты, можно заметить изменение направления на звезду — её параллактическое
(то есть кажущееся) смещение.
Такая же идея измерения расстояний была предложена и Николаем
Коперником после опубликования им гелиоцентрической системы мироустройства.
Однако ни Копернику, ни тем более Аристотелю не удалось обнаружить это
смещение.
Лишь к середине XIX века, когда на телескопы стали ставить оборудование для
точного измерения углов, удалось измерить такое смещение у ближайших звёзд. Как
удалось установить, кажущееся перемещение более близкой звезды на фоне очень
далёких звёзд происходит по эллипсу с периодом в один год и отражает движение
наблюдателя вместе с Землёй вокруг Солнца. Этот небольшой эллипс, который
описывает звезда, называется параллактическим эллипсом.
В угловой мере его большая полуось равна величине угла, под
которым со звезды видна большая полуось земной орбиты, перпендикулярная
направлению на звезду. Этот угол называется годичным параллаксом и
обозначается греческой буквой π или латинской буквой р.
Зная годичное параллактическое смещение звезды, можно легко
определить расстояние до неё:
В записанной формуле а — это
средний радиус земной орбиты.
Если учесть, что годичные параллаксы звёзд измеряются десятитысячными
долями секунды, а большая полуось земной орбиты равна одной астрономической
единице, то можно получить формулу для вычисления расстояния до звезды в
астрономических единицах:
Первые надёжные измерения годичного параллакса были
осуществлены почти одновременно в Германии, России и Англии в 1837 году.
В России первые измерения годичного параллакса были проведены
Василием Яковлевичем Струве для яркой звезды Северного полушария Веги. Давайте
по его данным определим расстояние до этой звезды.
Согласитесь, что для измерения расстояний до звёзд
астрономическая единица слишком мала. Даже ближайшая к нам звезда —
альфа-Центавра — расположена более чем в 273,5 тысячах а. е. Поэтому для
удобства определения расстояний до звёзд в астрономии применяется специальная
единица длины — парсек (сокращённо пк), название
которой происходит от двух слов — «параллакс» и «секунда».
Парсек — это расстояние, с которого средний радиус
земной орбиты, перпендикулярный лучу зрения, виден под углом в одну угловую
секунду:
1 пк
= 206 265 а. е. =30,8586 трлн км.
Исходя из определения, расстояние в парсеках равно обратной
величине годичного параллакса:
Вернёмся к нашей задаче и определим расстояние до Веги в
парсеках, воспользовавшись полученным нами уравнением.
Также, помимо парсека, в астрономии используется ещё одна
внесистемная единица измерения расстояний — световой год.
Световой год — это расстояние, которое свет,
распространяясь в вакууме, проходит за один год:
1 пк
= 3,26 св. г. = 206 265 а. е. = 3 ∙ 1013 км.
В 1989 году Европейским космическим агентством был запущен
спутник «Гиппаркос». За 37 месяцев своей работы ему удалось
измерить годичные параллаксы более чем миллиона звёзд. При этом точность
измерений для более ста тысяч из них составила одну угловую миллисекунду.
Однако после того, как астрономы научились определять
расстояния до звёзд, возникла ещё одна проблема. Оказалось, что звёзды,
находящиеся примерно на одинаковом расстоянии от Земли, могут отличаться друг
от друга по видимой яркости (блеску). При этом видимый блеск не характеризует
реального излучения звезды. Например, Солнце нам кажется самым ярким объектом
на небе лишь потому, что оно находится гораздо ближе к Земле, чем остальные
звёзды. Поэтому для сравнения истинного блеска звёзд необходимо было определять
их звёздную величину на определённом одинаковом расстоянии от Земли. За такое
одинаковое (или стандартное) расстояние принято 10 пк. Видимая звёздная величина, которую
имела бы звезда, если бы находилась от нас на расстоянии 10 пк,
называется абсолютной звёздной величиной.
Почему в качестве эталонного расстояния было выбрано 10
парсек? Да для простоты расчётов. Итак, предположим, что видимая звёздная
величина звезды на некотором расстоянии D равна т а её блеск — I.
Напомним, что блеск двух источников, звёздные величины
которых отличаются на единицу, отличаются в 2,512 раза. То есть для двух звёзд,
звёздные величины которых равны т1 и т2
соответственно, отношение их блесков выражается соотношением:
Тогда по определению видимая звёздная величина звезды с
расстояния в 10 пк будет равна абсолютной звёздной
величине М. Если обозначить блеск звезды на этом расстоянии через I0, то для
видимой и абсолютной звёздных величин одной и той же звезды предыдущее
уравнение будет выглядеть так:
В тоже время из физики известно, что блеск меняется обратно
пропорционально квадрату расстояния:
Подставим данное выражение в предыдущее уравнение, при этом
учтём, что :
Теперь прологарифмируем полученное выражение:
И упростим его:
Если учесть, что расстояние до звезды обратно пропорционально
её годичному параллаксу, то получим формулу, по которой можно вычислить
абсолютную звёздную величину близко расположенных к нам звёзд
Теперь давайте по полученной формуле рассчитаем абсолютную
звёздную величину нашего Солнца. Для этого учтём, что его видимая звёздная
величина равна–26,8т, а среднее расстояние до него составляет
одну астрономическую единицу
То есть наше Солнце выглядит слабой звёздочкой почти пятой
звёздной величины.
Зная абсолютную звёздную величину звезды, можно вычислить её
действительное общее излучение или светимость.
Светимостью называют полную энергию, излучаемую
звездой за единицу времени. Светимость звезды можно выразить в ваттах, но чаще
её выражают в светимостях Солнца.
Используя формулу Погсона, можно записать соотношение между светимостями
и абсолютными звёздными величинами какой-либо звезды и Солнца:
Данную формулу можно переписать, если учесть, что светимость
Солнца принята за единицу, а его абсолютна звёздная величина равна 4,8m:
По светимости (то есть мощности излучения) звёзды значительно
отличаются друг от друга. Так мощность излучения некоторых звёзд-сверхгигантов
больше мощности излучения Солнца в 330 тыс. А некоторые звёзды-карлики,
обладающие наименьшей светимостью, излучают свет в 480 тыс. раз слабее нашего
Солнца.